Przeczytaj
W tym materiale, analizując wykresy wybranych funkcji elementarnych, określimy ich granice w nieskończoności a następnie wykorzystamy poznane wiadomości do obliczenia granic innych funkcji.
Niech: , i .
Wykresy funkcji , gdzie i , wyglądają następująco:
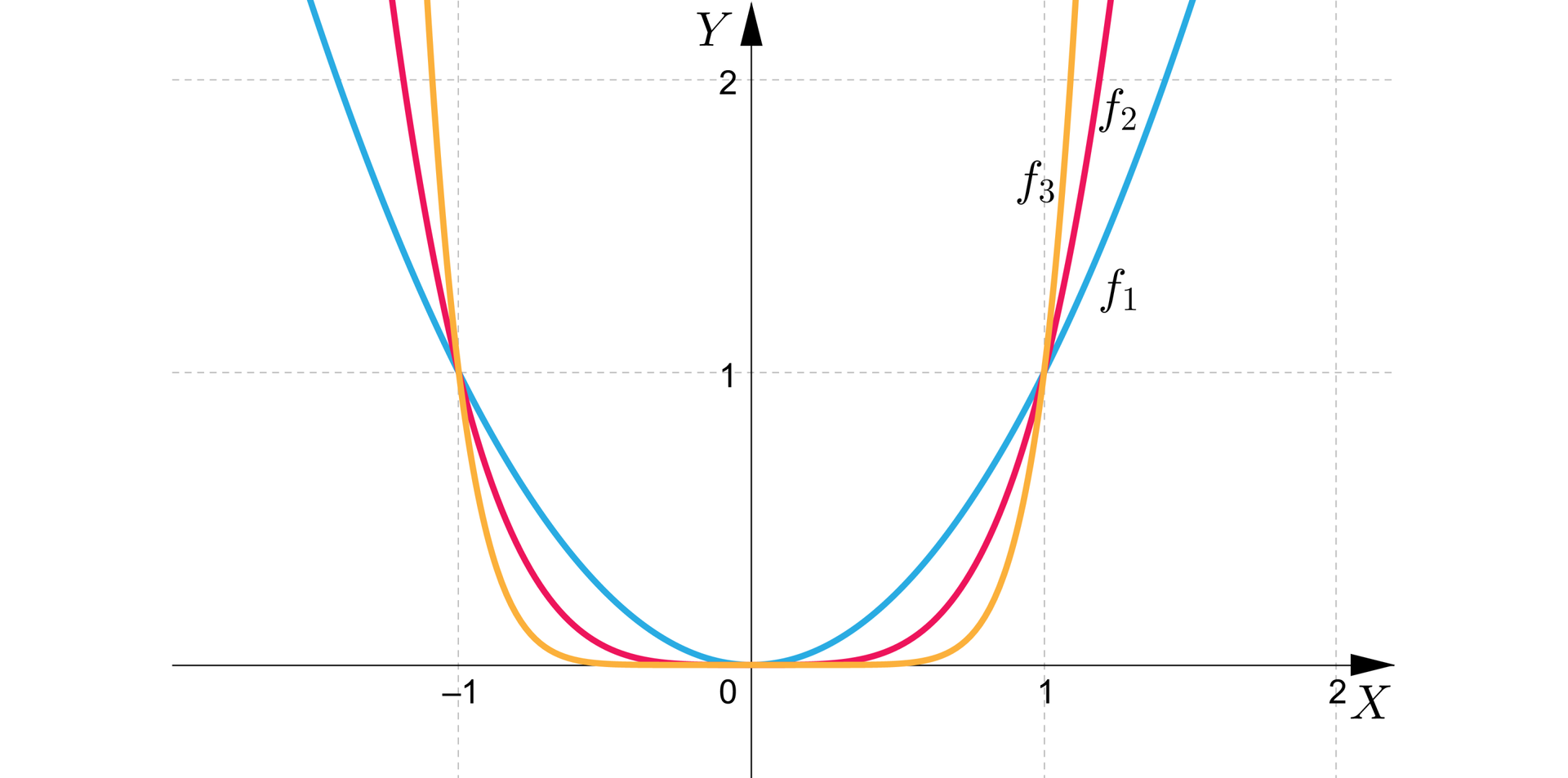
Widzimy, że gdy:
argumenty dążą do plus nieskończoności, to wartości funkcji też dążą do plus nieskończoności, co zapisujemy następująco:
,
argumenty dążą do minus nieskończoności, to wartości funkcji dążą do plus nieskończoności, co zapisujemy następująco:
.
Analizowane funkcje są parzyste, więc
Wniosek
Jeżeli funkcja jest postaci , gdzie i , to .
Niech: , i .
Wykresy funkcji , i wyglądają następująco:

Na podstawie wykresów możemy stwierdzić, że dla każdego :
Analizowane funkcje są nieparzyste, więc
Wniosek
Jeżeli funkcja jest postaci , gdzie i to i .
Niech: , i .
Wykres funkcji , dla wygląda następująco:

Widzimy, że gdy:
argumenty dążą do plus nieskończoności, to wartości funkcji też dążą do plus nieskończoności, co zapisujemy następująco
,
argumenty dążą do minus nieskończoności, to wartości funkcji zbliżają się do osi , czyli dążą do zera, co zapisujemy
.
Wykres funkcji , dla wygląda następująco:

Z wykresu odczytujemy:
Wniosek
Jeżeli funkcja jest postaci , gdzie , to
i , gdy ,
i , gdy .
Niech , , gdzie i .
Gdy wykres funkcji wygląda następująco:

Gdy argumenty dążą do plus nieskończoności, wartości funkcji też zmierzają do plus nieskończoności: .
Możemy również zauważyć, że wykres tej funkcji ma asymptotę pionową prawostronną , ponieważ .
Wykres funkcji , gdy :
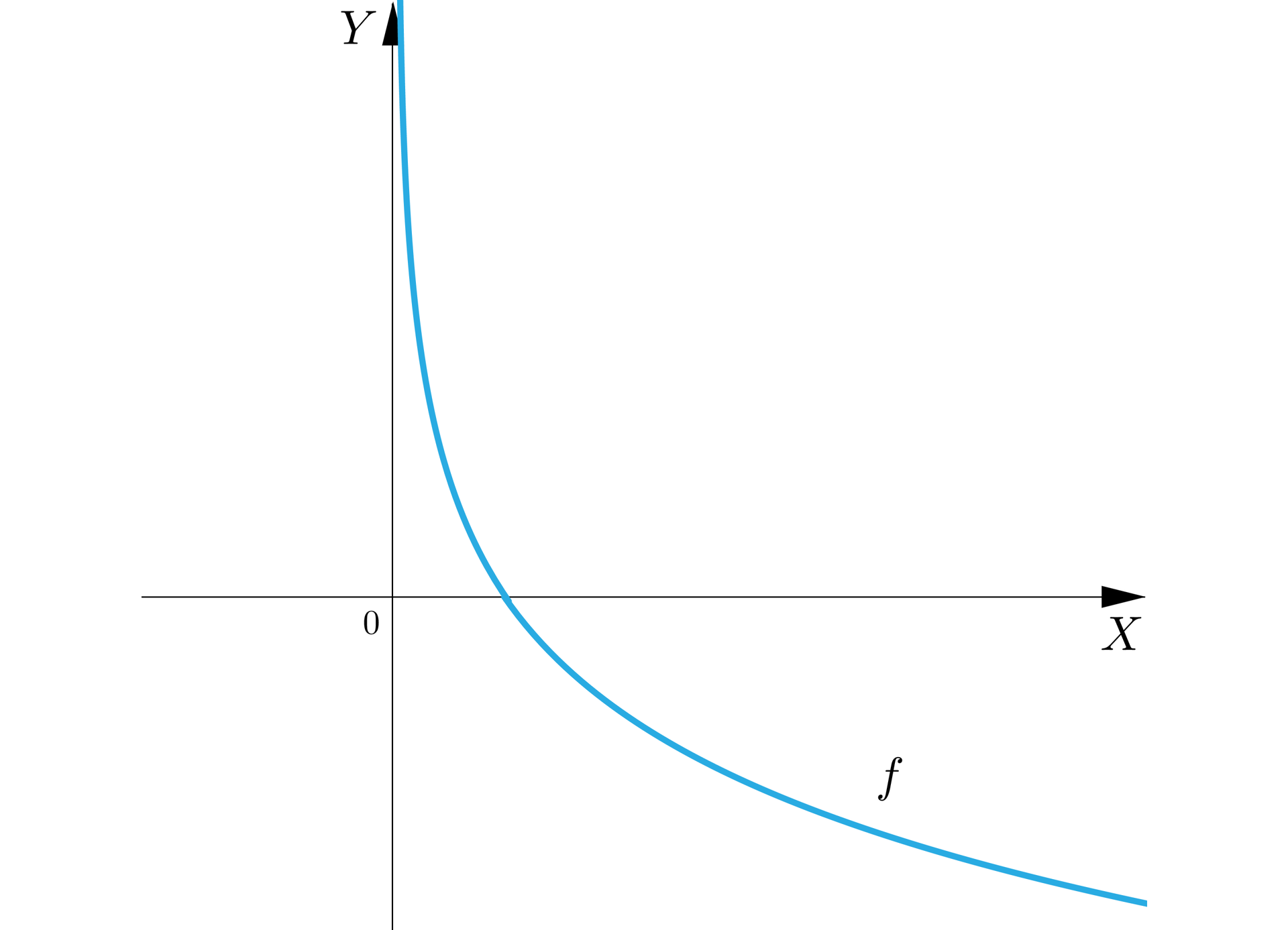
Widzimy, że gdy , to .
Możemy również zauważyć, że wykres tej funkcji ma asymptotę pionową prawostronną ponieważ .
Wniosek
Jeżeli funkcja jest postaci , gdzie , to
, gdy ,
, gdy .
Niech , .
Wykres tej funkcji wygląda następująco:
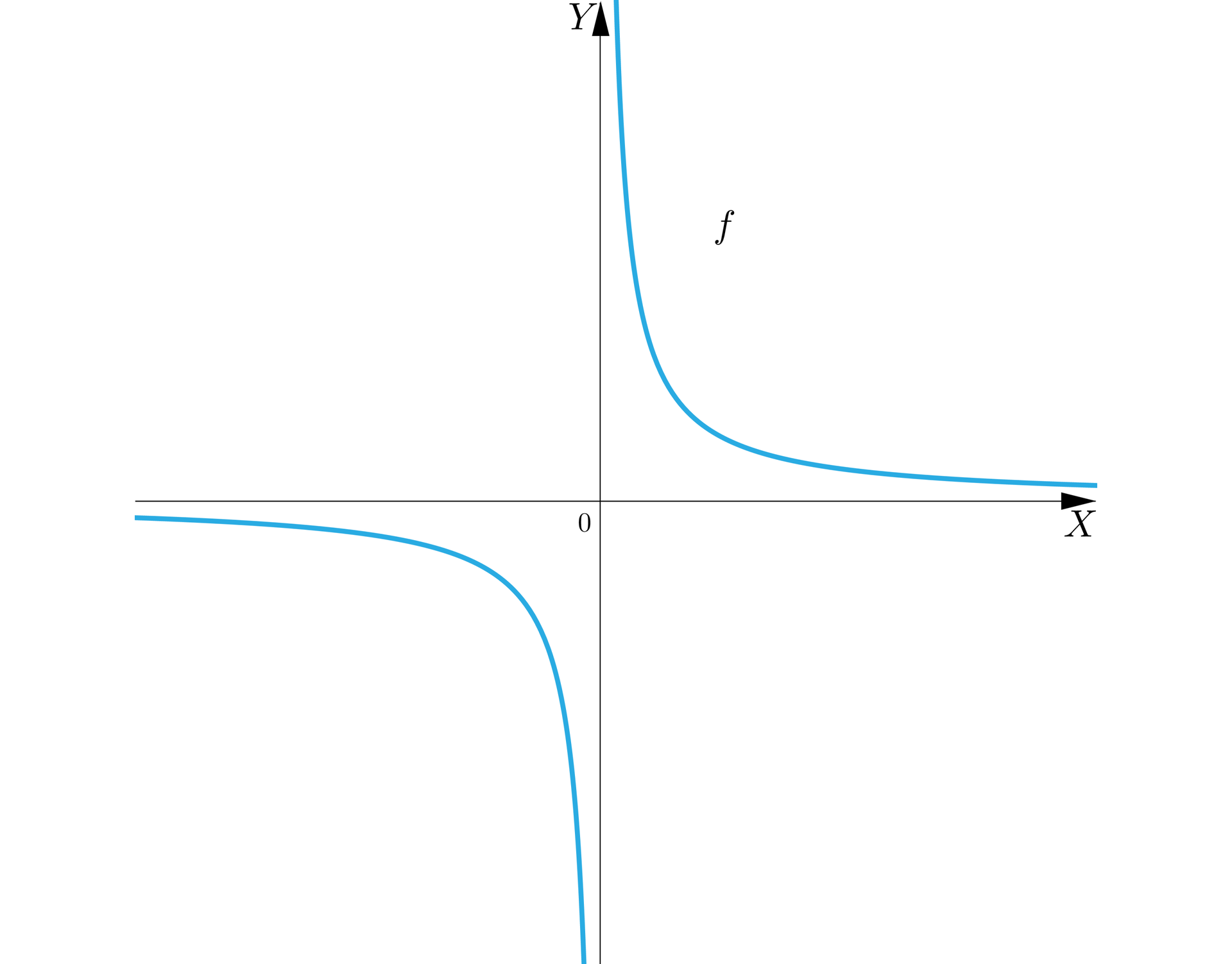
Możemy podać granicę tej funkcji w plus i minus nieskończoności.
Widzimy, że zarówno przy zmierzającym do plus jak i minus nieskończoności wykres zbliża się do osi , czyli:
Możemy również zauważyć, że wykres tej funkcji ma asymptotę pionową obustronną , bo istnieją granice niewłaściweniewłaściwe:
Wniosek
Jeżeli funkcja jest postaci , gdzie , to
Niech ,
Narysujemy teraz wykres funkcji
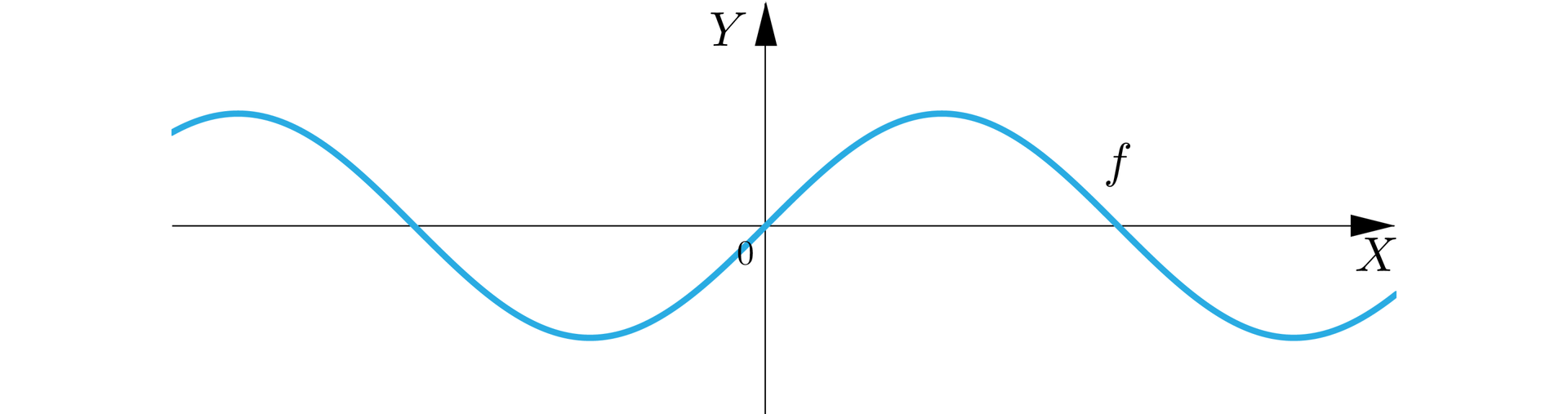
Z wykresu tej funkcji wynika, że nie istnieje granica tej funkcji w plus i minus nieskończoności. Aby to wykazać skorzystamy z definicji Heinego granicy funkcji.
Załóżmy, że przedział , gdzie , zawiera się w dziedzinie funkcji . Granicą funkcji w plus nieskończoności jest liczba , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do odpowiadający mu ciąg wartości funkcji jest zbieżny do liczby .
Weźmy dwa ciągi rozbieżne do nieskończoności: oraz określone wzorami:
oraz .
Ponieważ funkcja jest funkcją okresową o okresie zasadniczym to , więc:
i .
co oznacza, że nie istnieje granica .
Podobnie można wykazać, że nie istnieje granica tej funkcji, gdy .
Obliczymy granicegranice funkcji , gdy dąży do i gdy dąży do .
Rozwiązanie
Dziedziną funkcji określonej wzorem jest zbiór .
W przypadku, gdy liczymy granicę wielomianu, wyłączamy przed nawias zmienną w najwyższej potędze: .
Zauważmy, że granica funkcji zarówno przy dążącym do , jaki i przy dążącym do , zależy jedynie od granicy wyrażenia .
Ponadto:
,
.
Zatem:
.
Analogicznie liczymy granicę przy .
Ponieważ
,
,
więc
.
Wniosek
Jeżeli jest wielomianem stopnia parzystego zmiennej , to zarówno przy dążącym do jak i przy dążącym do funkcja ta dąży do nieskończoności o takim znaku, jak znak współczynnika przy najwyższej potędze zmiennej .
Obliczymy granicę funkcji , gdy dąży do i gdy dąży do .
Rozwiązanie
Dziedziną funkcji określonej wzorem jest zbiór .
W przypadku, gdy liczymy granicę wielomianu, wyłączamy przed nawias zmienną w najwyższej potędze: .
Zauważmy, że granica funkcji zarówno przy dążącym do jak i przy dążącym do zależy jedynie od granicy wyrażenia .
Mamy:
zatem:
i stąd: .
Liczymy teraz granicę .
Ponieważ:
,
więc .
Wniosek
Gdy dąży do , to wielomian stopnia nieparzystego zmiennej dąży do nieskończoności z takim znakiem, jaki ma współczynnik przy najwyższej potędze zmiennej , a gdy dąży do , to wielomian dąży do nieskończoności ze znakiem przeciwnym do znaku współczynnika przy najwyższej potędze zmiennej .
Obliczymy granicę .
Rozwiązanie
Dziedziną funkcji określonej wzorem jest zbiór gdyż .
Dla dążącego do funkcja dąży do i funkcja też zmierza do , zatem otrzymujemy symbol nieoznaczony.
W przypadku, gdy liczymy granicę funkcji wymiernej, wyłączamy przed nawias, w liczniku i mianowniku, zmienną w najwyższej potędze, w której występuje ona w mianowniku – w tym przypadku .
Wyrażenie zapisujemy zatem następująco:
.
Ponieważ
, i ,to
.
Zauważmy, że dla dążącego do nasze rozumowanie dotyczące granicy funkcji się powtórzy. Taką samą sytuację będziemy mieli w każdym przypadku, gdy stopień licznika i stopień mianownika funkcji wymiernej będą równe.
Wniosek
Jeśli stopnie licznika i mianownika funkcji wymiernej są równe, to granica tej funkcji, gdy dąży do i gdy dąży do , jest równa ilorazowi współczynników przy zmiennych w najwyższej potędze.
Obliczymy granicę funkcji w nieskończoności.
Rozwiązanie
Liczymy następującą granicęgranicę .
Ponieważ obliczenie na tym etapie granicy jest niemożliwe, bo otrzymujemy wyrażenie nieoznaczone, mnożymy i dzielimy funkcję przez i stosujemy wzór .
Mamy zatem:
i stąd:
.
Ponownie otrzymaliśmy symbol nieoznaczony, dlatego wyrażenie przekształcamy dalej i wyłączamy z licznika i mianownika:
.
Słownik
funkcja ma dla dążącego do granicę niewłaściwą , jeżeli dla dowolnego ciągu argumentów funkcji rozbieżnego do odpowiadający mu ciąg wartości funkcji jest rozbieżny do , co zapisujemy następująco
granicą funkcji dla dążącego do jest liczba , jeżeli dla każdego ciągu argumentów funkcji rozbieżnego do odpowiadający mu ciąg wartości funkcji jest zbieżny do liczby