Przeczytaj
Przekrojem bryły nazywamy figurę płaską, która powstaje przez przecięcie bryły płaszczyzną – jest to część wspólna bryły i płaszczyzny.
Będziemy zajmować się przekrojami sześcianu. Dokonamy klasyfikacji przekrojów sześcianu ze względu na kształt przekroju.
Podział przekrojów sześcianu ze względu na kształt
PrzekrójPrzekrój sześcianu może być trójkątem, czworokątem, pięciokątem lub sześciokątem.
Przekrój trójkątny
Wśród wierzchołków trójkąta, który jest przekrojem sześcianu, znajduje się jeden, dwa lub trzy wierzchołki sześcianu lub też nie znajduje się żaden wierzchołek sześcianu – przy czym, jeśli są to dwa wierzchołki, to nie są one końcami tej samej krawędzi sześcianu.
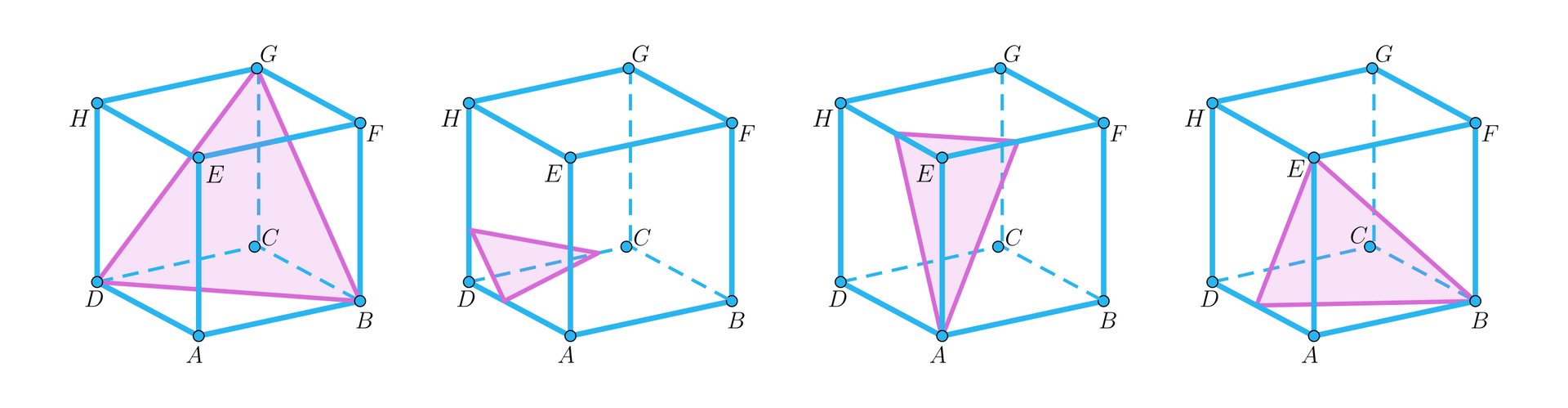
Sześcian przecinamy płaszczyzną jak na rysunku:

Pokażemy, że jeśli , to przekrój jest trójkątem równoramiennym.
Rozwiązanie
Wprowadźmy oznaczenie oraz . Z twierdzenia Pitagorasa mamy oraz . A zatem . Czyli trójkąt jest równoramienny.
Aby przekrój sześcianu był trójkątem, wszystkie jego wierzchołki muszą leżeć na trzech różnych krawędziach sześcianu wychodzących z jednego wierzchołka.
Pokażemy, korzystając z uwagi powyżej, że przekrójprzekrój sześcianu nie może być trójkątem prostokątnym.
Rozwiązanie
Oznaczmy przez , , odległości wierzchołków trójkąta od wspólnego wierzchołka krawędzi, na których leżą wierzchołki trójkąta (przy czym , bo w przeciwnym przypadku trójkąt nie byłby przekrojem) oraz przez , , długości boków tego trójkąta.
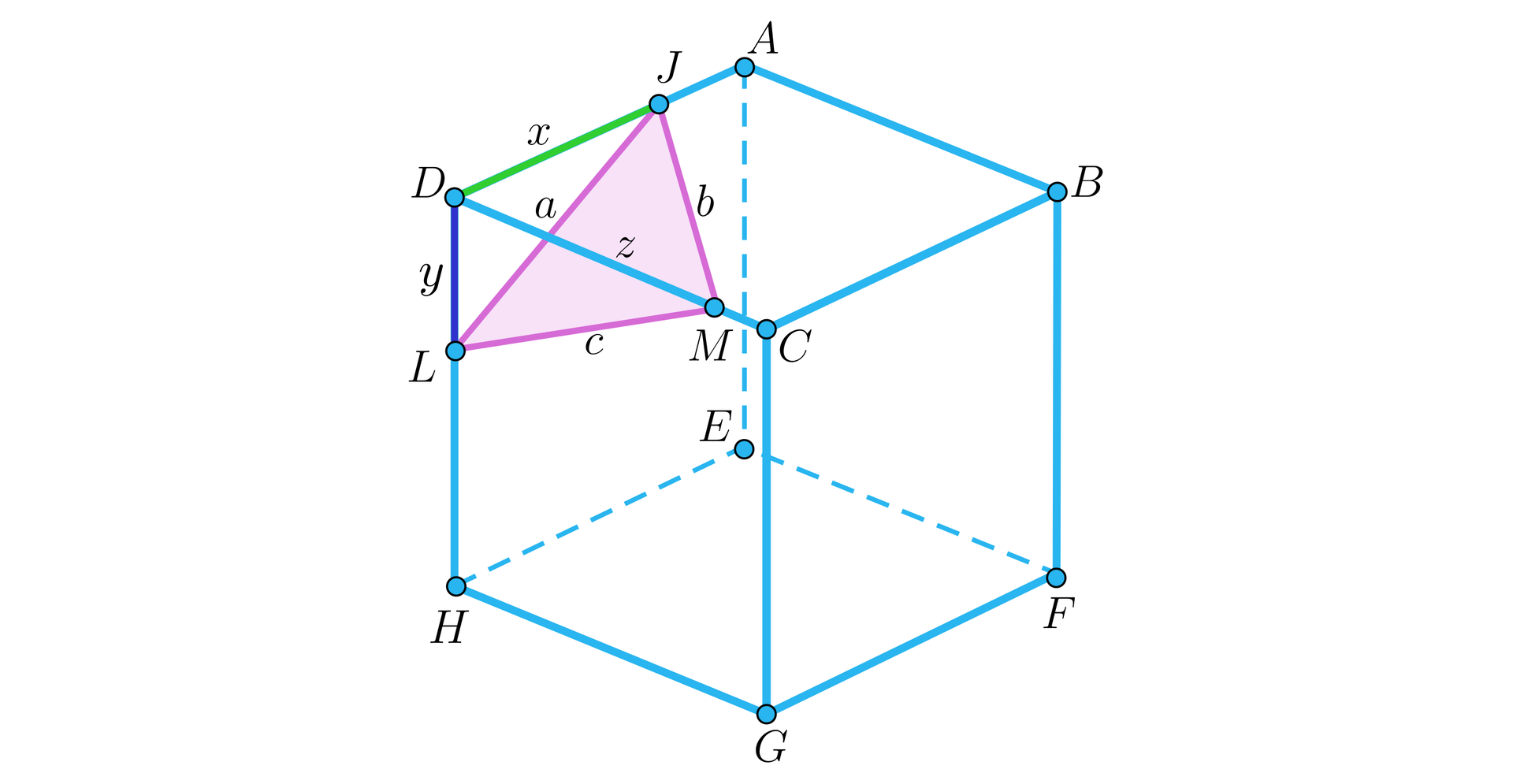
Z twierdzenia Pitagorasa mamy:
Zauważmy, że:
A zatem z twierdzenia odwrotnego do twierdzenia Pitagorasa żaden z kątów w tym trójkącie nie jest prosty.
Ponieważ przy oznaczeniach w powyższym przykładzie:
to wszystkie kąty w przekroju trójkątnym sześcianu są ostre.
Wnioski
Przekrój trójkątny w sześcianie jest trójkątem ostrokątnym o dowolnych miarach kątów ostrych.
Przekrój trójkątny w sześcianie może być trójkątem równobocznym. Największym trójkątem równobocznym, który może być przekrojem sześcianu jest trójkąt, którego wierzchołki są wierzchołkami sześcianu, a boki są przekątnymi ścian bocznych.
Przekrój czworokątny
Mamy wiele przekrojówprzekrojów sześcianu w kształcie czworokąta.
Kwadrat
Przekrój, którego wszystkie boki są prostopadłe do odpowiednich krawędzi sześcianu, jest kwadratem.

Prostokąt niebędący kwadratem

Przekrój w kształcie prostokąta otrzymamy przecinając sześcian płaszczyzną prostopadłą do ściany sześcianu. Przy czym, jeśli płaszczyzna ta będzie równoległa do płaszczyzny zawierającej krawędź tej ściany, to prostokąt ten będzie kwadratem.
Największym przekrojem w kształcie prostokąta, jaki otrzymamy, jest prostokąt, którego bokami są przeciwległe krawędzie sześcianu oraz przekątne jego ścian.

Równoległobok
Przekrój czworokątny sześcianu, którego po dwa wierzchołki znajdują się na równoległych ścianach, jest równoległobokiem.
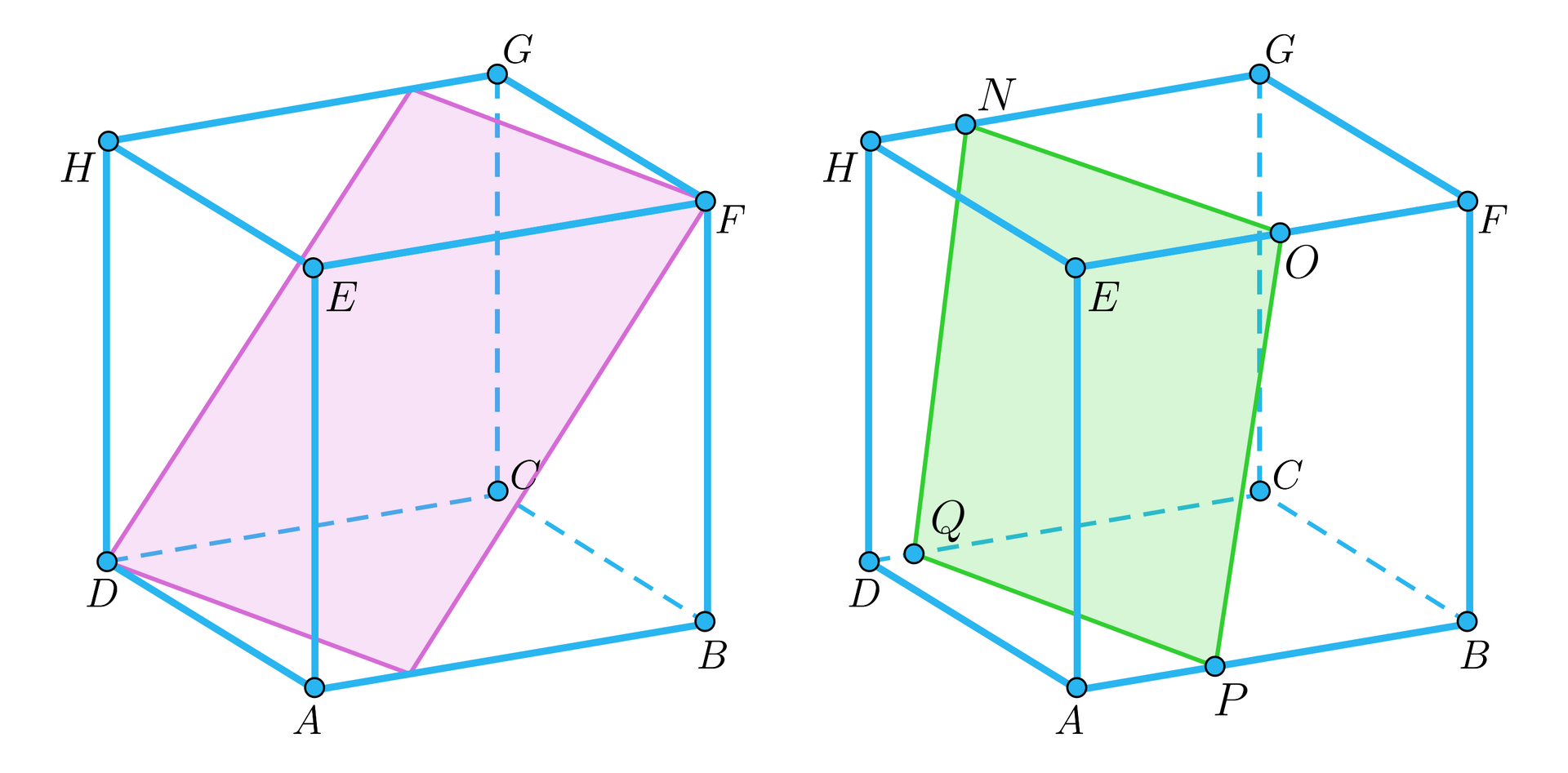
Pokażemy, że jeśli punkty i są środkami odcinków i w sześcianie na rysunku, to równoległobok jest rombem.
Rozwiązanie
Wprowadźmy oznaczenia na rysunku.

Zauważmy, że trójkąty , , , są trójkątami prostokątnymi o tych samych długościach przyprostokątnych, a zatem są przystające. Czyli . A zatem równoległobok jest rombem.
Trapez
Przekrój czworokątny sześcianu, którego dokładnie jedna para boków leży na równoległych ścianach, jest trapezem, który nie jest równoległobokiem.

Wniosek:
Aby przekrój był czworokątem, co najmniej jedna para boków tego przekroju musi leżeć na płaszczyznach równoległych. Przecięcie dwóch ścian równoległych trzecią płaszczyzną daje dwa równoległe boki przekroju. Zatem każdy przekrój sześcianu w kształcie czworokąta jest trapezem.
Przekrój pięciokątny
Jeżeli płaszczyzna przetnie pięć ścian sześcianu, to jest on pięciokątem.
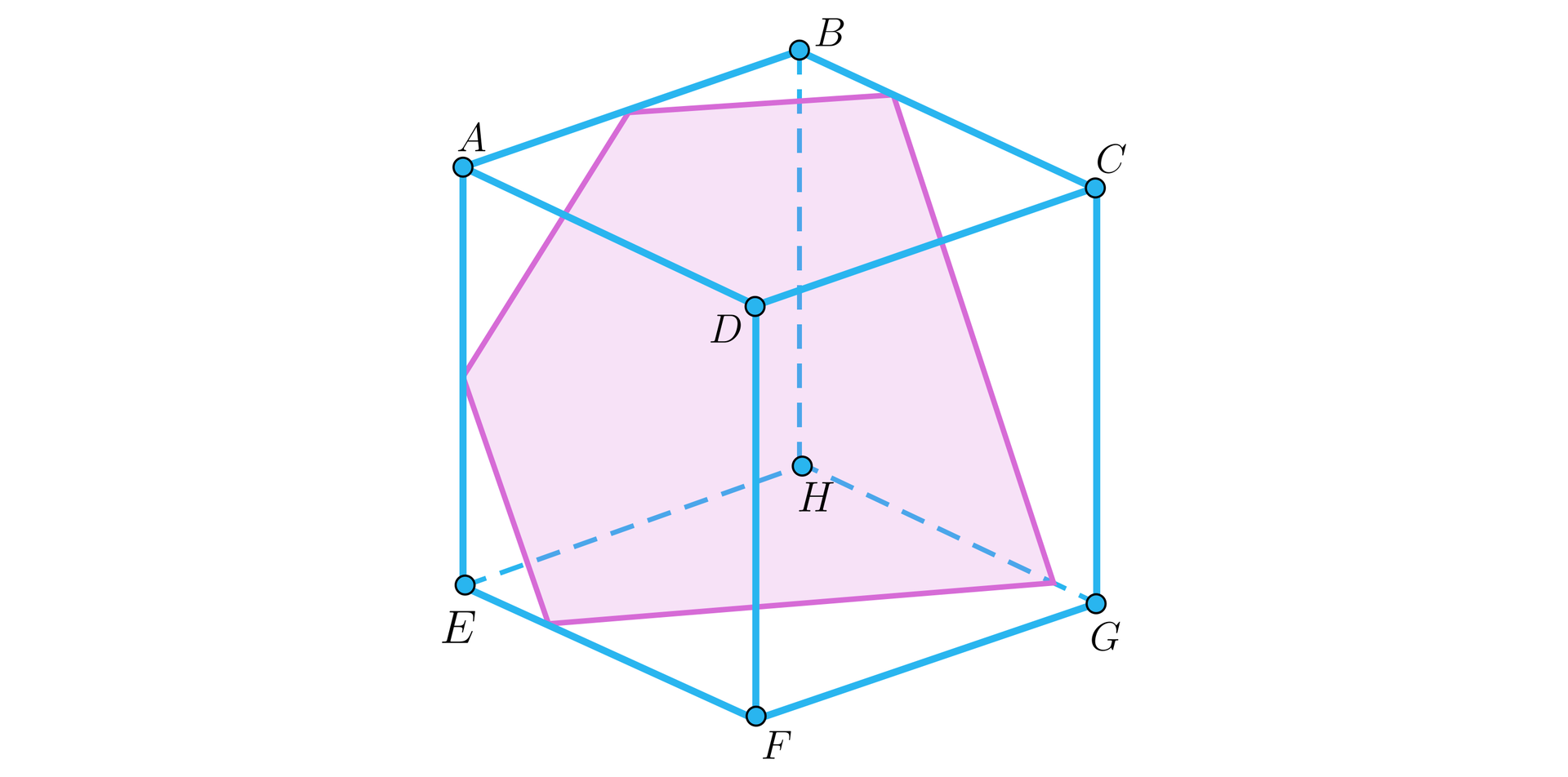
Nie istnieje przekrój sześcianu, który ma kształt pięciokąta foremnego.
Uzasadnij, że przekrój sześcianu nie może być pięciokątem foremnym.
Rozwiązanie
Zauważmy, że przecinając dwie równoległe płaszczyzny trzecią płaszczyzną otrzymujemy na przecięciu proste równoległe.
Ponieważ, aby otrzymać przekrój w kształcie pięciokąta musimy przeciąć pięć ścian sześcianu, to wśród nich są dwie pary ścian równoległych. A zatem pięciokąt ten ma dwie pary boków równoległych. Łatwo zauważyć, że pięciokąt foremny nie ma ani jednej pary boków równoległych.
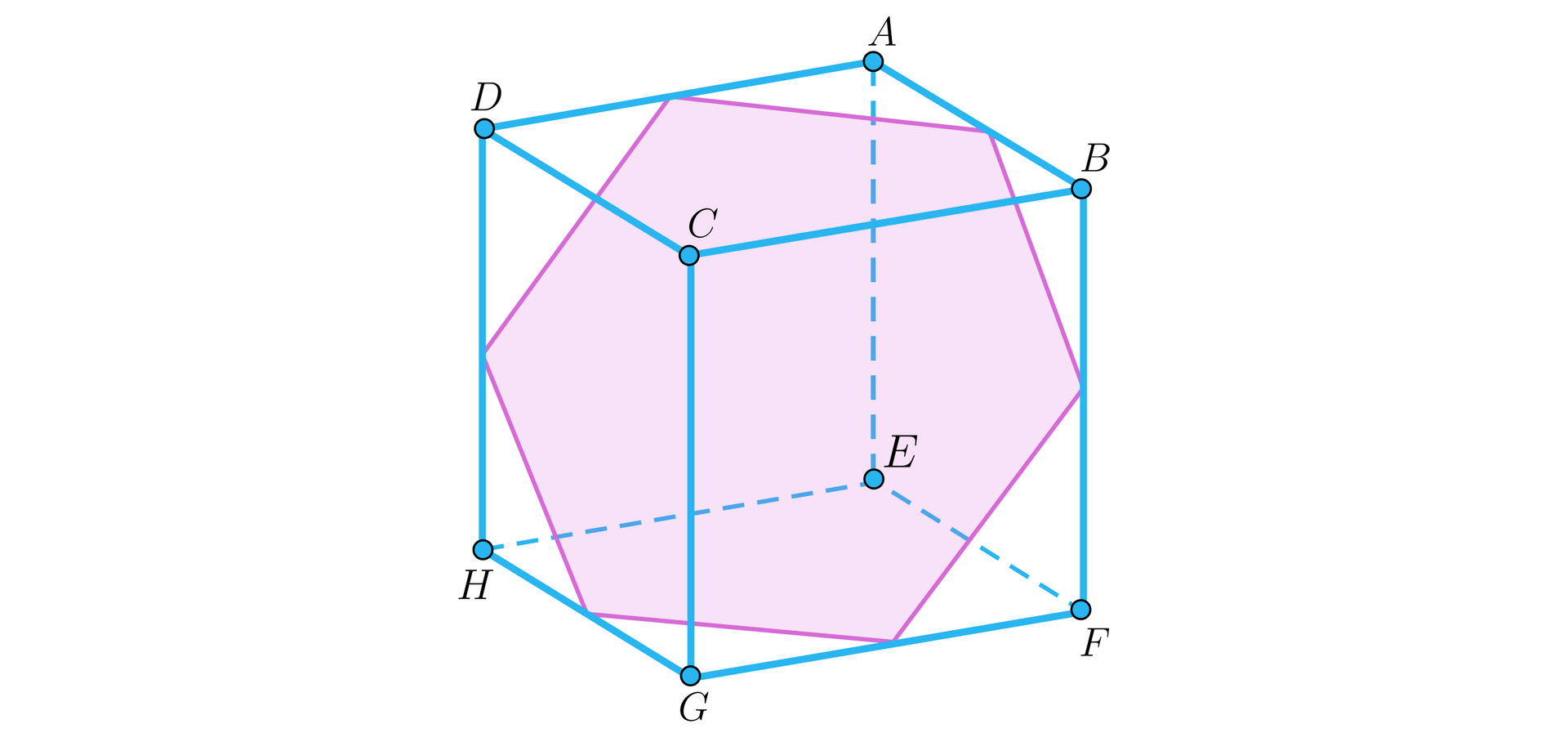
Przekrój sześciokątny

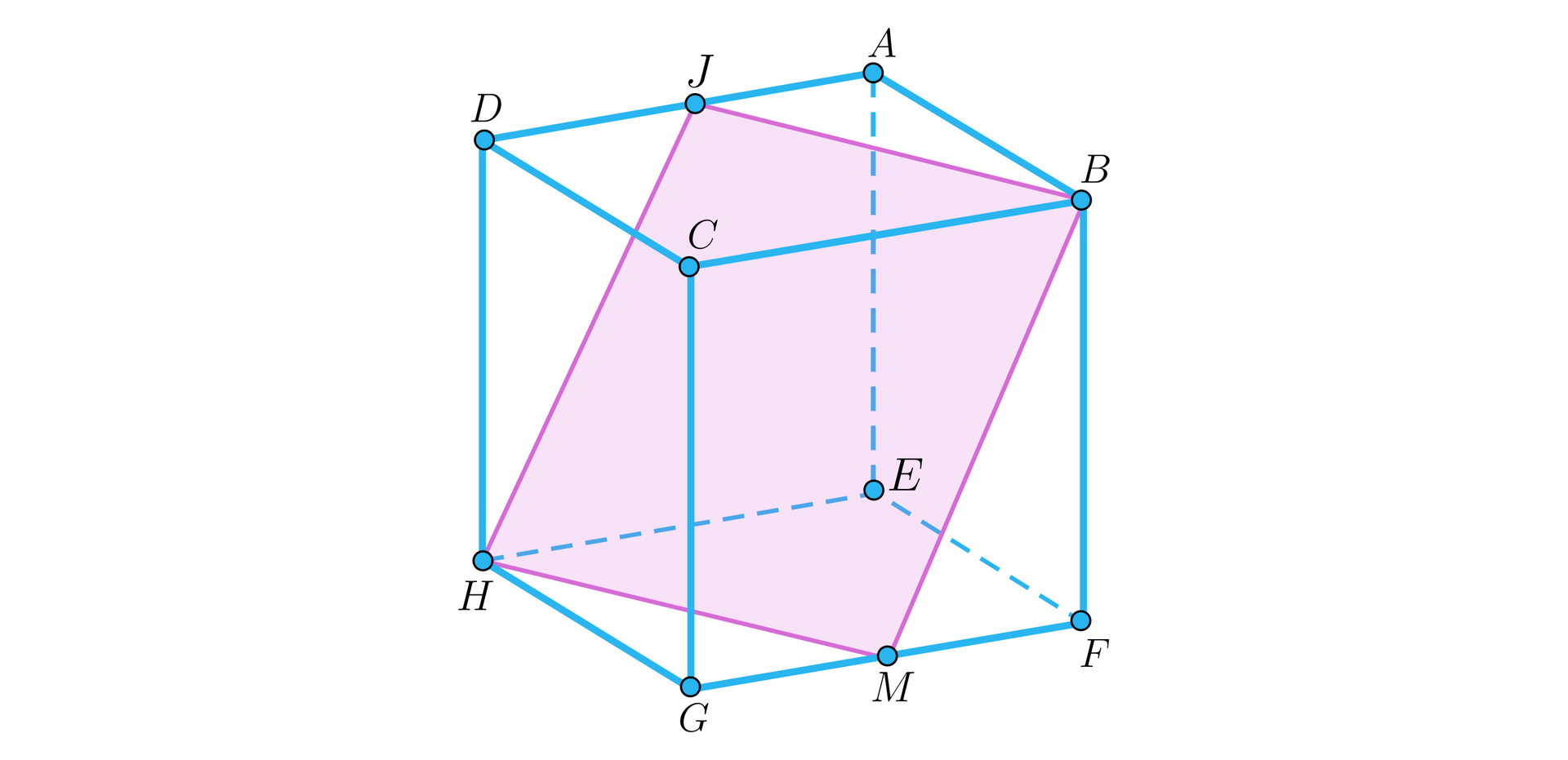
Sprawdź, czy istnieje przekrój sześcianu w kształcie sześciokąta foremnego.
Rozwiązanie
Przekrój sześciokątny przechodzący przez środki krawędzi , , , , , na rysunku poniżej jest sześciokątem foremnym. Wszystkie boki tego sześciokąta mają długość .
Słownik
figura płaska, która powstaje przez przecięcie bryły płaszczyzną – jest to część wspólna bryły i płaszczyzny