Zacznijmy od jednego z najbardziej podstawowych praw algebry, którego geometryczna interpretacja jest następująca: wyobraźmy sobie, że w prostokącie o bokach $a$ oraz $b$ bok długości $b$ wydłużono o $c$ jednostek (rysunek poniżej). Pole powstałego prostokąta jest równe $a·\left(b+c\right)$. Z drugiej strony jest ono równe sumie pól dwóch prostokątów o polach równych odpowiednio $ab$ oraz $ac$.
A zatem:

$a\cdot \left(b+c\right)=a\cdot b+a\cdot c$

RQ26KHqnArT8e

Grafika przedstawia dwa prostokąty przylegające do siebie dłuższym bokiem o długości a. Krótsze boki prostokątów mają odpowiednio długości b dla prostokąta niebieskiego oraz c dla prostokąta pomarańczowego.

Równość ta zwana jest prawem rozdzielności mnożenia względem dodawania. Gdy podstawimy w niej $-c$ za $c$, uzyskamy prawo rozdzielności mnożenia względem odejmowania:

$a\cdot \left(b-c\right)=a\cdot b-a\cdot c$.

Te dwie równości pozwalają przekształcać wiele prostych wyrażeń.

Wyrażenie:

$a·\left(a-c\right)+c·\left(a+b\right)$

zapiszemy bez użycia nawiasów.

Pozbywając się nawiasów, otrzymujemy: $a·\left(a-c\right)+c·\left(a+b\right)=a^2-ac+ac+bc=a^2+bc$.

Zauważmy, że zredukowaliśmy tu wyrazy podobne $-ac$ oraz $ac$.

Rozdzielność mnożenia względem dodawaniaprawo rozdzielności mnożenia względem dodawaniaRozdzielność mnożenia względem dodawania przydaje się też do obliczania w pamięci niektórych iloczynów. Na przykład, obliczając w pamięci iloczyn $52·7$, liczymy osobno iloczyn $50·7$ i osobno iloczyn $2·7$, a następnie dodajemy otrzymane wyniki. Zatem rozumowanie nasze przebiega według poniższego schematu:

$52·7=\left(50+2\right)·7=50·7+2·7=350+14=364$.

Zauważmy, że zastosowaliśmy wzór:

$a·\left(b+c\right)=ab+ac$ dla $a=7$, $b=50$, $c=2$.

Wykażemy, że pole litery $H$ na rysunku poniżej wyraża się wzorem: $P_H=2ab+bc-2cd$.

R1OWHm6bQlpi0

Grafika przedstawia wielobok o kształcie litery H tak, że są to dwa prostokąty o wysokości równej b i szerokości a połączone mniejszym prostokątem o większym boku równym c. Zarówno odległość od góry wysokości b do górnego boku mniejszego prostokąta, jak i od dolnego boku mniejszego prostokąta do podstawy całej figury H wynosi d. Całość oznaczona kolorem zielonym.

Możemy rozumować rozmaicie.

Sposób 1. Jeśli zieloną literę $H$ uzupełnimy dwoma błękitnymi prostokątami o wymiarach $c\times d$ (tzn. o bokach $c$ i $d$), to uzyskamy prostokąt (o czarnych bokach na rysunku) o wymiarach $\left(a+c+a\right)\times b$.

RhwdDfqrSZ9p1

Grafika przedstawia wielobok o kształcie litery H tak, że są to dwa prostokąty o wysokości równej b i szerokości a połączone mniejszym prostokątem o większym boku równym c. Zarówno odległość od góry wysokości b do górnego boku mniejszego prostokąta, jak i od dolnego boku mniejszego prostokąta do podstawy całej figury H wynosi d. Całość oznaczono kolorem zielonym . Niebieskim kolorem oznaczono prostokąty tworzone przez długości c i d.

Stąd pole niebieskiej litery $H$ możemy obliczyć, odejmując od pola prostokąta o wymiarach $\left(2a+c\right)\times b$ pola dwóch prostokątów o wymiarach $c\times d$:

$P=\left(2a+c\right)·b-2cd=2ab+bc-2cd$.

Sposób 2. Dodajemy pola dwóch czerwonych prostokątów o bokach $a$ i $b$ oraz pole pomarańczowego prostokąta. Jeden z boków pomarańczowego prostokąta ma długość $c$. Długość drugiego boku tego prostokąta jest różnicą wysokości „boku litery $H$” i wysokości dwóch „nóżek litery $H$”, czyli wynosi $b-2d$.

R7lp3ldfIdzpo

Grafika przedstawia wielobok o kształcie litery H tak, że są to dwa prostokąty o wysokości równej b i szerokości a połączone mniejszym prostokątem o większym boku równym c. Zarówno odległość od góry wysokości b do górnego boku mniejszego prostokąta, jak i od dolnego boku mniejszego prostokąta do podstawy całej figury H wynosi d. Dwa większe prostokąty oznaczono kolorem czerwonym natomiast mniejszy kolorem pomarańczowym. Oznaczono również krótszy bok mniejszego prostokąta jako $b-2d$.

Stąd:

$P=2ab+c·\left(b-2d\right)=2ab+bc-2cd$.

Zauważmy, że niezależnie od sposobu rozumowania wynik jest taki sam. W pierwszej fazie może on być odmiennie zapisany, ale po pozbyciu się nawiasów - zgodnie z prawami algebry - musimy otrzymać zawsze sumę tych samych składników.

Rozpatrzmy teraz mnożenie sumy $\left(a+b\right)$ przez sumę $\left(c+d\right)$. Dwukrotnie korzystając z rozdzielności mnożenia względem dodawania, otrzymujemy:

$\left(a+b\right)·\left(c+d\right)=a·\left(c+d\right)+b·\left(c+d\right)=ac+ad+bc+bd$.

Ten algebraiczny fakt także ma prostą interpretację geometryczną: pole prostokąta o bokach $\left(a+b\right)$ oraz $\left(c+d\right)$ jest równe:

$P=\left(a+b\right)·\left(c+d\right)$.

Z drugiej strony pole to jest sumą pól kolorowych prostokątów (rysunek poniżej), czyli jest równe:

RAYDae1H3dYlu

Ilustracja przedstawia kwadrat na który składają się cztery prostokąty. Na boki dużego kwadratu składają się długości a i b oraz c i do. Czerwony prostokąt ma długości a i c , niebieski b i c , zielony b i d, a żółty d i a.

$P=ac+ad+bc+bd$.

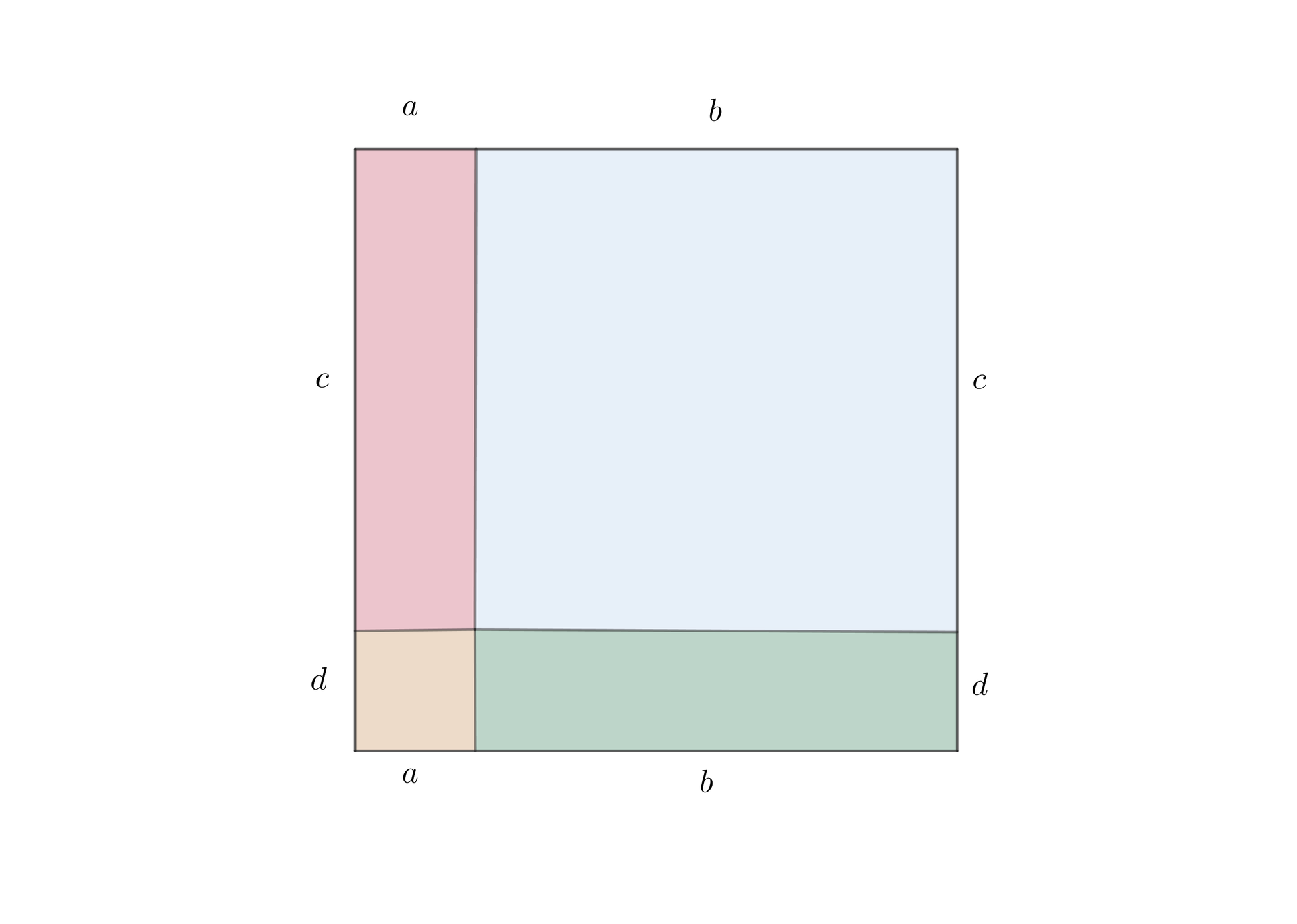
A zatem:

$\left(a+b\right)·\left(c+d\right)=ac+ad+bc+bd$.

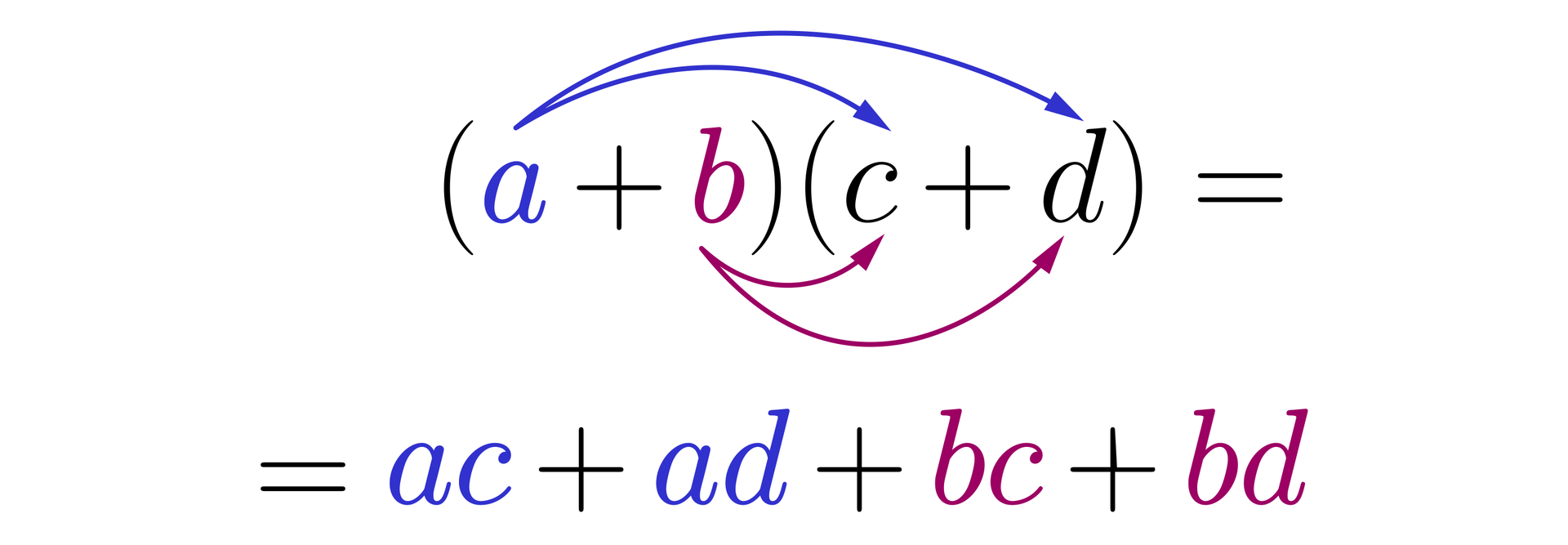
Stosując prawo rozdzielności mnożenia względem dodawania pokażemy, jak bez używania kalkulatora obliczyć $51·98$.

Obliczamy zgodnie z poznanymi zasadami:

$51\cdot 98=\left(50+1\right)\cdot 98=50\cdot 98+1\cdot 98=50\cdot \left(100-2\right)+1\cdot \left(100-2\right)=$

$=50\cdot 100-50\cdot 2+1\cdot 100-1\cdot 2=5000-2=4998$.

Odp. $51·98=4998$.

Uprościmy wyrażenie: $W=\left(x-2y\right)·\left(x+y\right)+xy$.

Najpierw pozbywamy się nawiasów:

$W=\left(x-2y\right)·\left(x+y\right)+xy=x^2+xy-2xy-2y^2+xy$.

Następnie redukujemy wyrazy podobne:

$W=\left(x-2y\right)·\left(x+y\right)+xy=x^2+\mathit{x}\mathit{y}\mathbf{-}\mathbf{2}\mathit{x}\mathit{y}-2y^2+\mathit{x}\mathit{y}=x^2-2y^2$.

A zatem:

$W=x^2-2y^2$.

Obliczymy teraz w inny sposób pole litery $H$ z przykładu $5$.

RDtQwQ7qq3AUo

Grafika przedstawia wielobok o kształcie litery H tak, że na dwóch prostokątach o wysokości d i podstawie a położony jest prostokąt o podstawie $c+2a$ i wysokości $b-2d$. Na nim z kolei stoją kolejne prostokąty o wysokości d i postawie a.

Pole to jest sumą pól czterech pomarańczowych prostokątów o wymiarach $a\times d$ i jednego zielonego prostokąta o wymiarach $\left(b-2d\right)\times \left(c+2a\right)$.

Stąd:

$P=4ad+\left(b-2d\right)·\left(c+2a\right)=4ad+bc+2ab-2dc-4ad=2ab+bc-2cd$.

Oczywiście, wynik ten zgadza się z naszymi poprzednimi obliczeniami.

Z pięciu przystajacych zielonych  prostokątów utworzono literę $P$ tak, jak to widać na poniższym rysunku.

R13HCn2d80ngD

Grafika przedstawia figurę P złożona z pięciu przystających zielonych prostokątów oraz dwóch czerwonych kwadratów. Zielone prostokąty tworzą literę P a czerwone kwadraty wypełnienie tła. U dołu znajduje się jeden prostokąt o krótszym boku jako podstawie i większy z kwadratów. Nad nimi znajdują się prostokąty okalające kwadrat tak ,że na bok tworzonego wspólnie kwadratu składa się długość sumaryczna krótszego i dłuższego boku zielonego prostokąta.

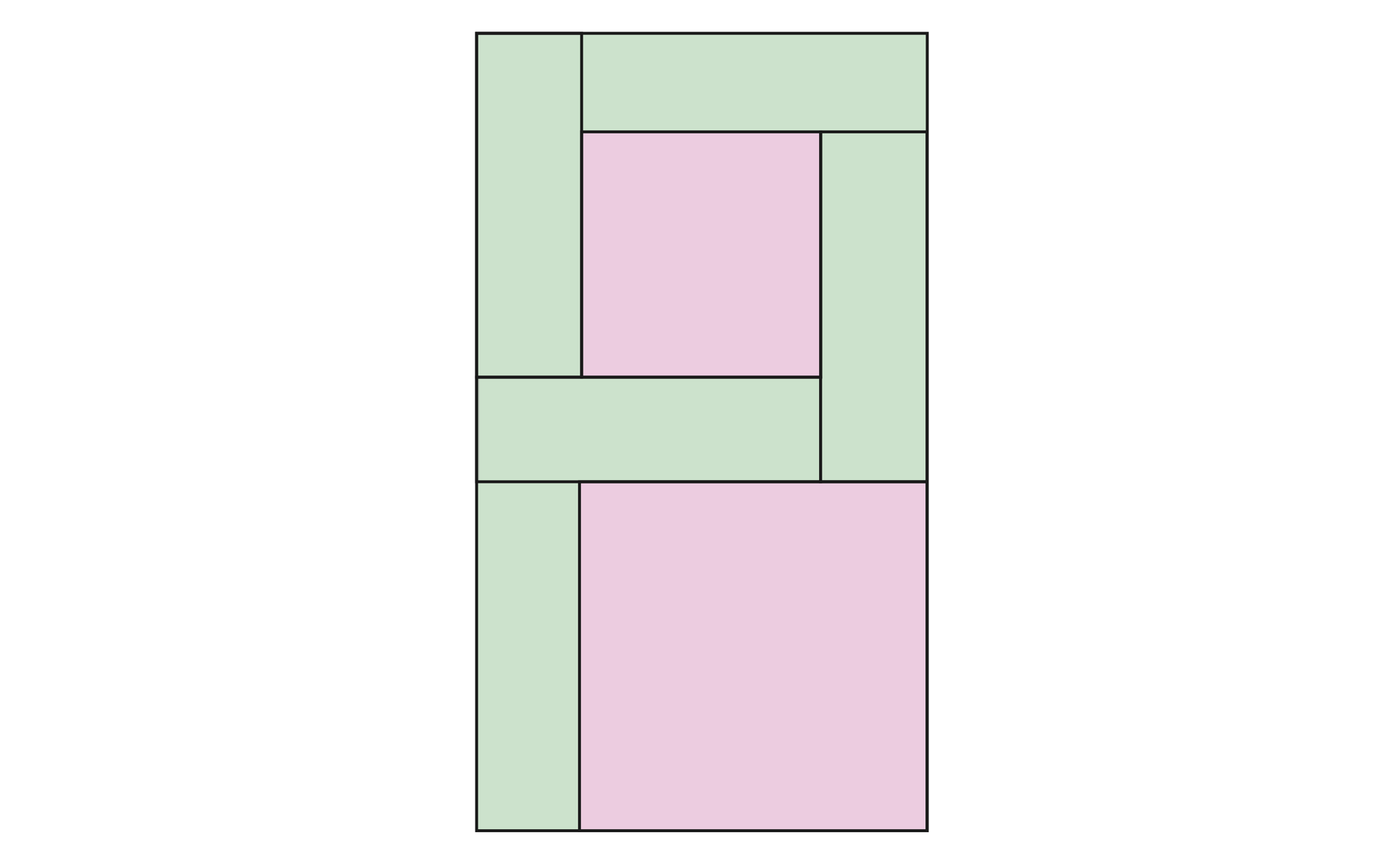
Pole widocznego na nim większego z fioletowych  kwadratów jest równe $S$, a pole mniejszego fioletowego  kwadratu jest równe $T$. Obliczymy pole figury  $P$ w zależności od $S$ oraz $T$.

Oznaczmy długości: krótszego boku zielonego  prostokąta przez $x$, a dłuższego boku - przez $y$.

Ponieważ, jak to odczytujemy z rysunku, długość boku większego z fioletowych  kwadratów jest równa $y$, a długość boku mniejszego fioletowego  kwadratu jest równa $y-x$, więc $y=\sqrt{S}$ oraz $y-x=\sqrt{T}$, skąd $x=\sqrt{S}-\sqrt{T}$.

Litera $P$ zbudowana jest z pięciu przystajacych zielonych  prostokątów o bokach $x$ i $y$, zatem jej pole jest równe $5xy=5·\left(\sqrt{S}-\sqrt{T}\right)·\sqrt{S}=5S-5\sqrt{ST}$.

$a\cdot \left(b+c\right)=a\cdot b+a\cdot c$