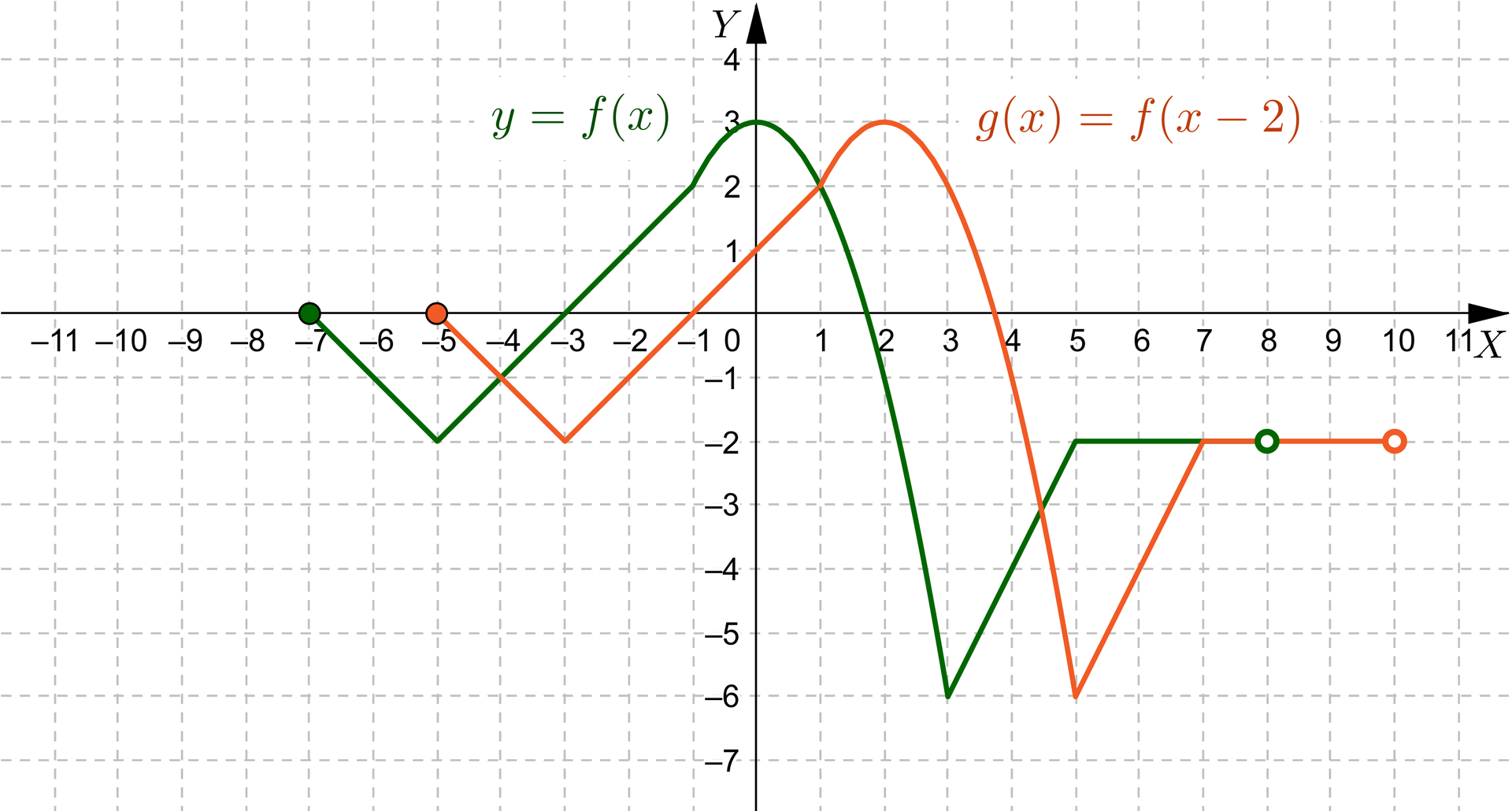Przeczytaj
Wykres funkcji to zbiór wszystkich punktów postaci , gdzie jest dowolnym argumentem z dziedziny funkcjidziedziny funkcji , a jest wartością funkcji dla argumentu .
Jeśli punktpunkt należy do wykresu funkcji , to .
W układzie współrzędnych każdej parze liczb odpowiada dokładnie jeden punktpunkt.
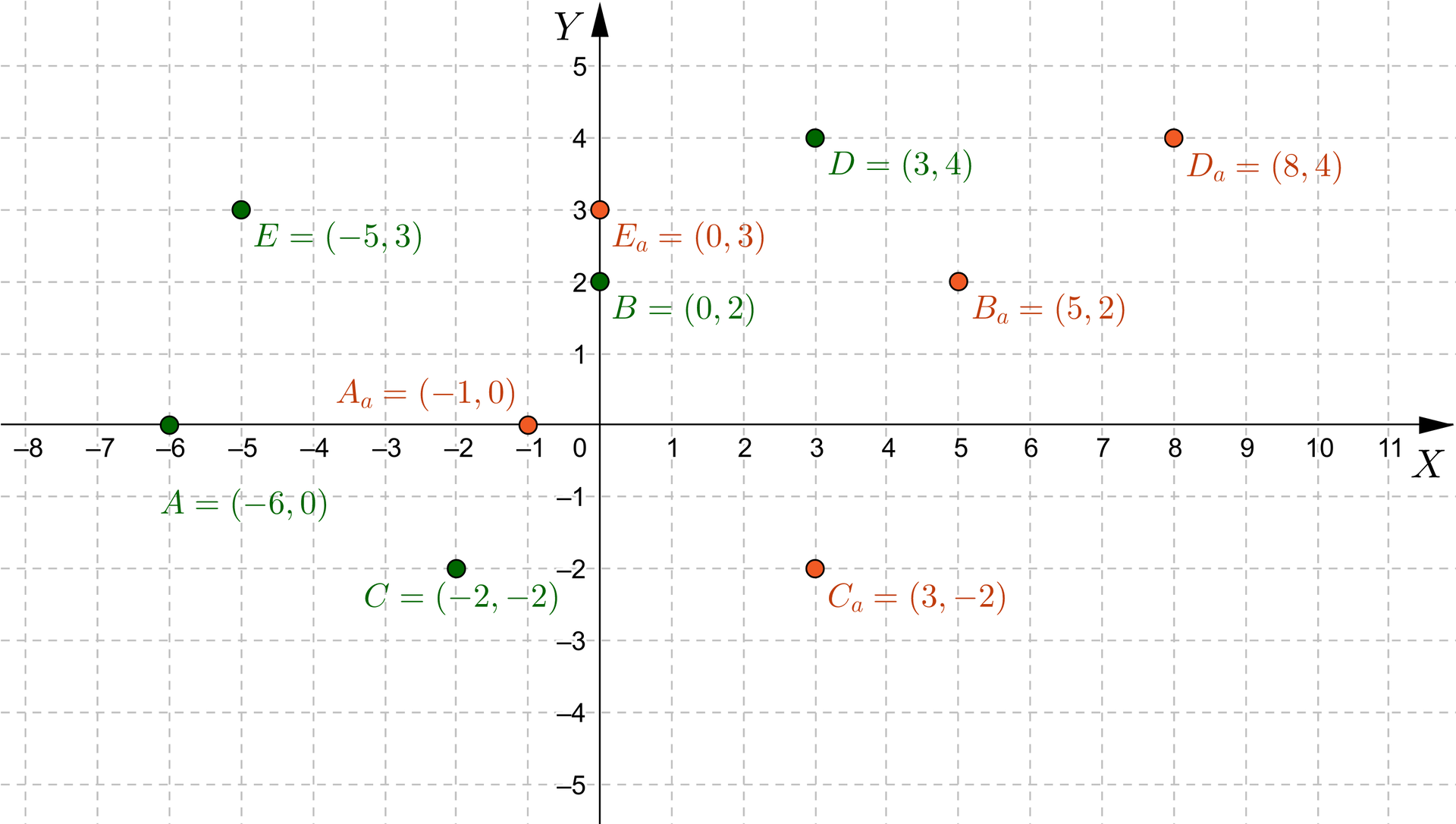
Dany jest punktpunkt . Wyznaczymy współrzędne punktu:
a) , który otrzymamy w wyniku przesunięcia punktu o cztery jednostki w prawo wzdłuż osi ,
b) , który otrzymamy w wyniku przesunięcia punktu o cztery jednostki w lewo wzdłuż osi ,
c) , który otrzymamy w wyniku przesunięcia punktu o jednostek wzdłuż osi , gdzie jest liczbą rzeczywistą.

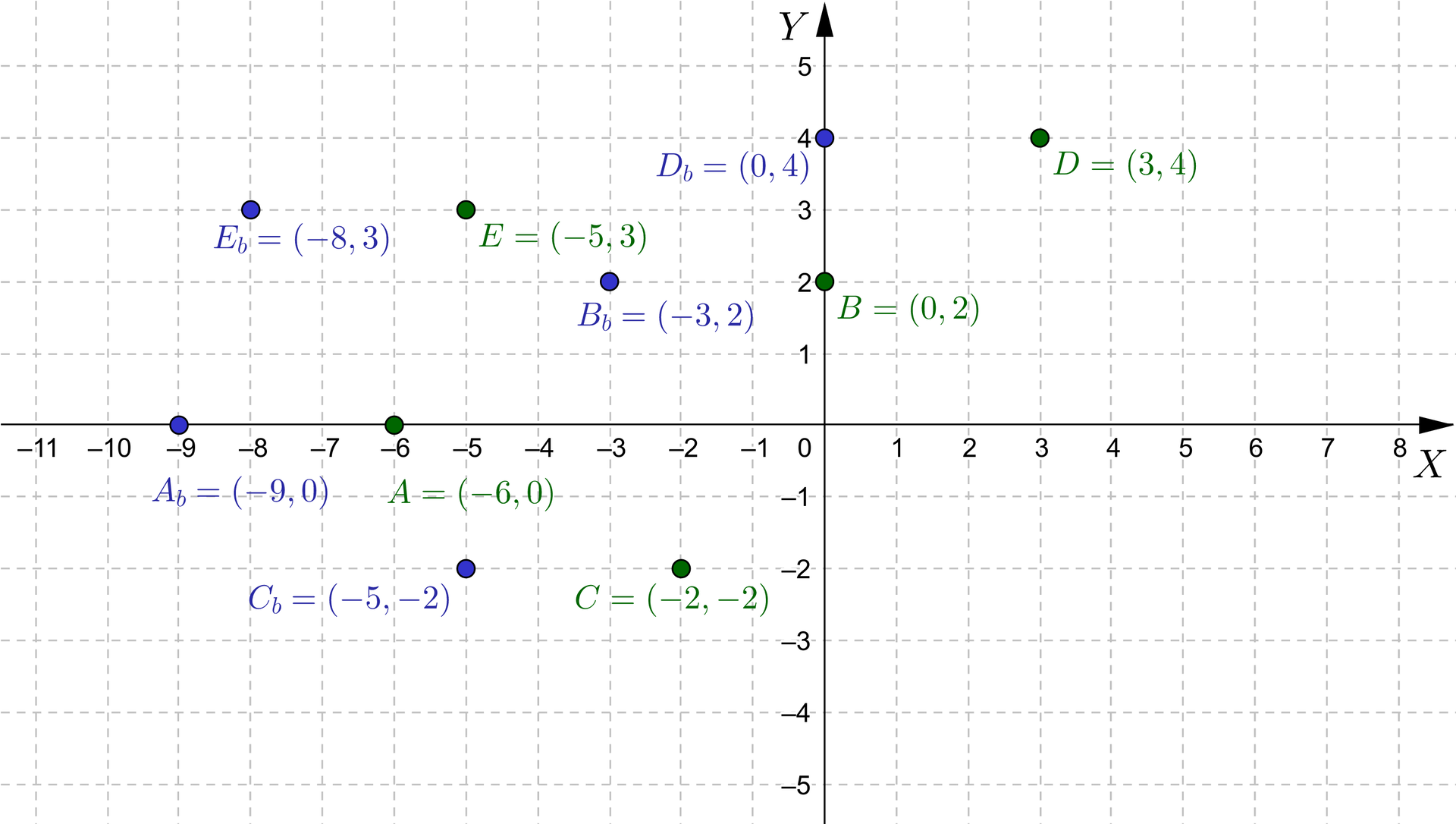
Dany jest wykres funkcji . Sporządzimy wykres funkcji otrzymany w wyniku:
a) przesunięcia danego wykresu o jednostek w prawo wzdłuż osi ,
b) przesunięcia danego wykresu o jednostki w lewo wzdłuż osi .

Wykres danej funkcji to zbiór pięciu punktów. Aby otrzymać wykres funkcji w wyniku przesunięcia wzdłuż osi należy każdy punktpunkt przesunąć analogicznie jak robiliśmy to w przykładzie 1.
W kolejnym przykładzie będziemy przesuwać wzdłuż osi wykres funkcji , . W przykładzie zwrócimy uwagę na dziedzinędziedzinę nowej funkcji oraz jej wzór.
Aby sporządzić wykres funkcji skorzystamy z tabeli częściowej, dzięki której będziemy mieli punkty o współrzednych całkowitych, które będą punktami przesuwanymi.
Zwróćmy uwagę na poniższy interaktywny wykres. Przesuwając suwakiem można zauważyć jak zmienia się dziedzinadziedzina oraz wzór funkcji w zależności od przesunięcia.
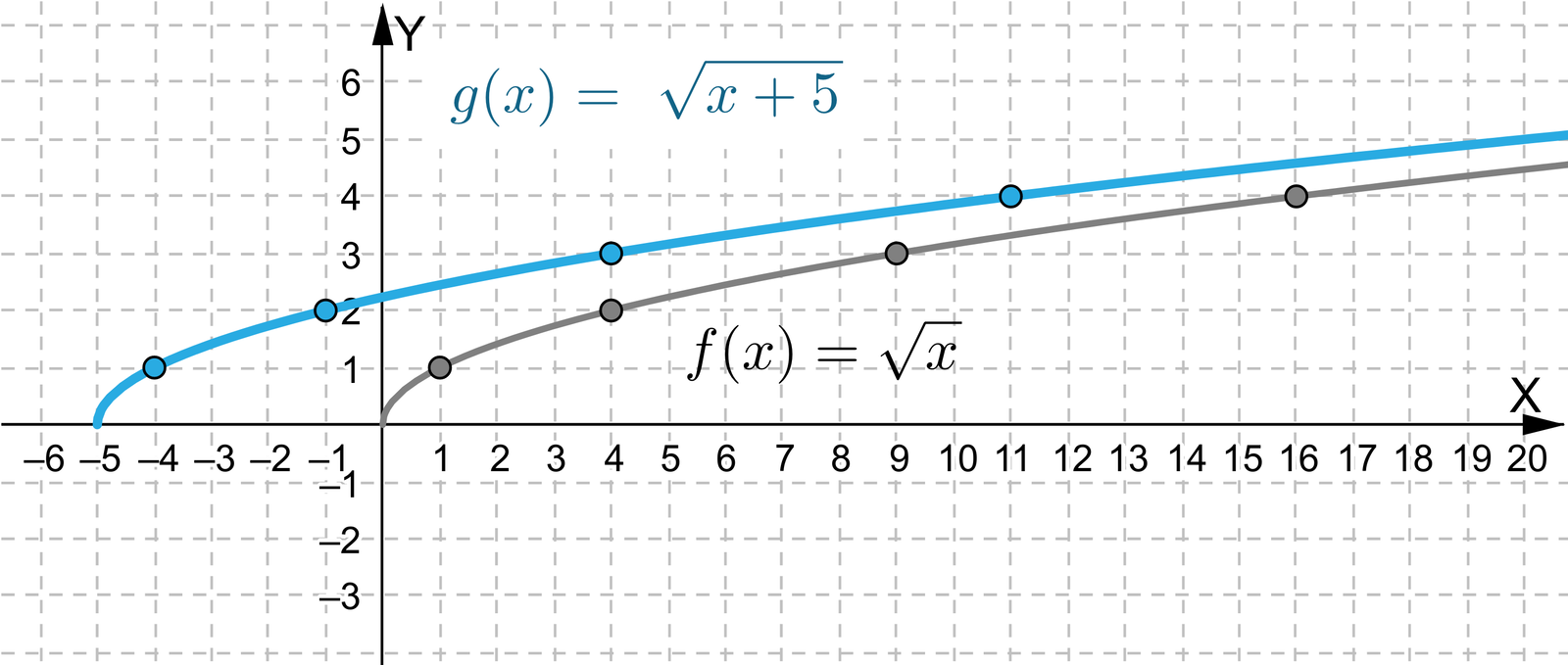
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DhD2JFoqv
Wyprowadzimy zależność między wzorem , a wzorem danej funkcji i liczbą o którą przesuwamy dany wykres wzdłuż osi .

Jeżeli przesuwamy wykres funkcji wzdłuż osi o jednostek, gdzie , to:
w wyniku przesunięcia w prawo otrzymamy wykres funkcji ,
w wyniku przesunięcia w lewo otrzymamy wykres funkcji .
Zwracamy uwagę jak zmienia się wzór funkcji otrzymanej w wyniku przesunięcia wzdłuż osi
gdy przesuwamy wykres o 3 jednostki w prawo, wówczas każdy argument we wzorze funkcji zamieniamy na argument ,
gdy przesuwamy wykres o 6 jednostek w lewo, wówczas każdy argument we wzorze funkcji zamieniamy na argument .

Poćwiczymy przesuwanie wykresu funkcji znając jej wykres oraz wzór funkcji . Dany jest wykres funkcji
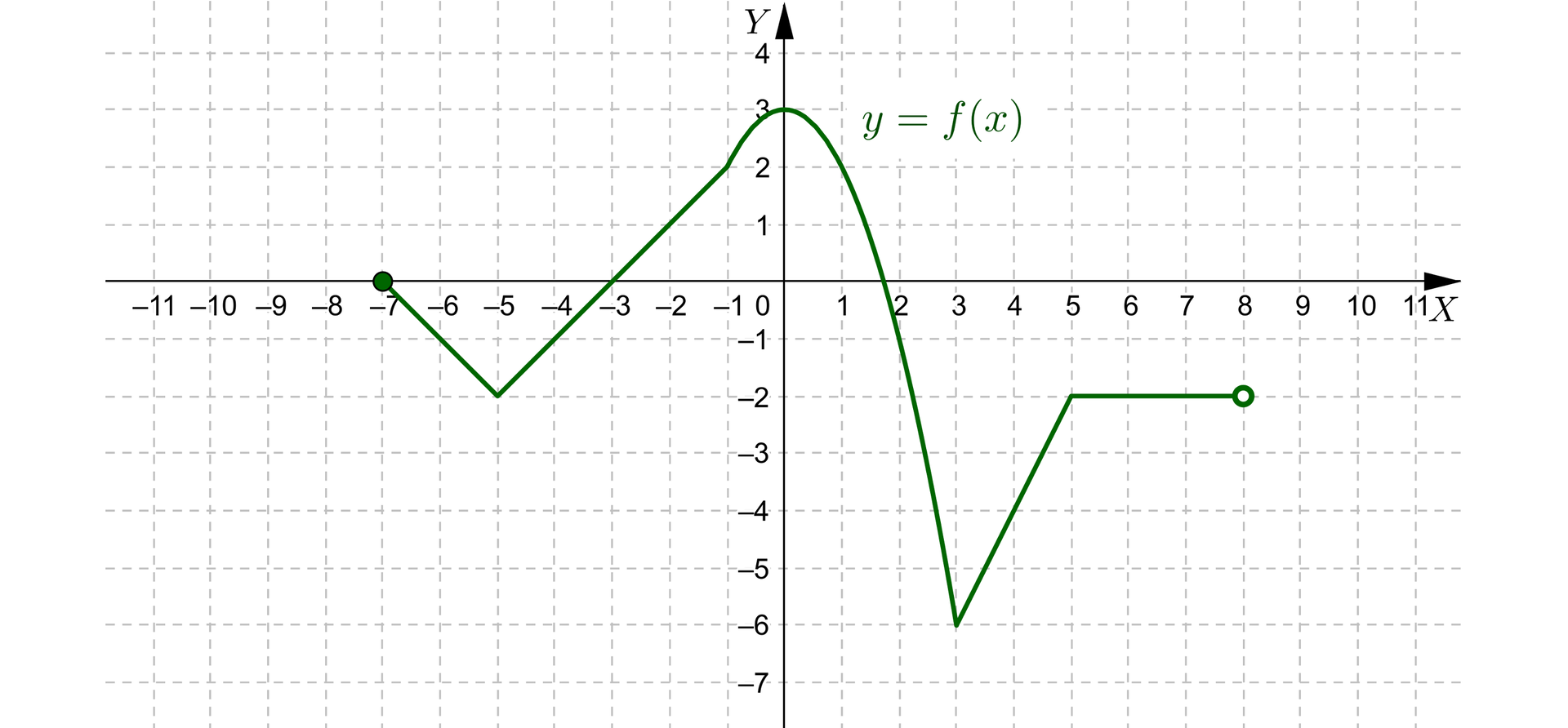
Sporządzimy wykres funkcji:
a)
b)
Przesunięcie wykresu funkcji wzdłuż osi ma wpływ na:
dziedzinędziedzinę funkcji ,
miejsca zerowemiejsca zerowe funkcji ,
przedziały monotoniczności funkcji .
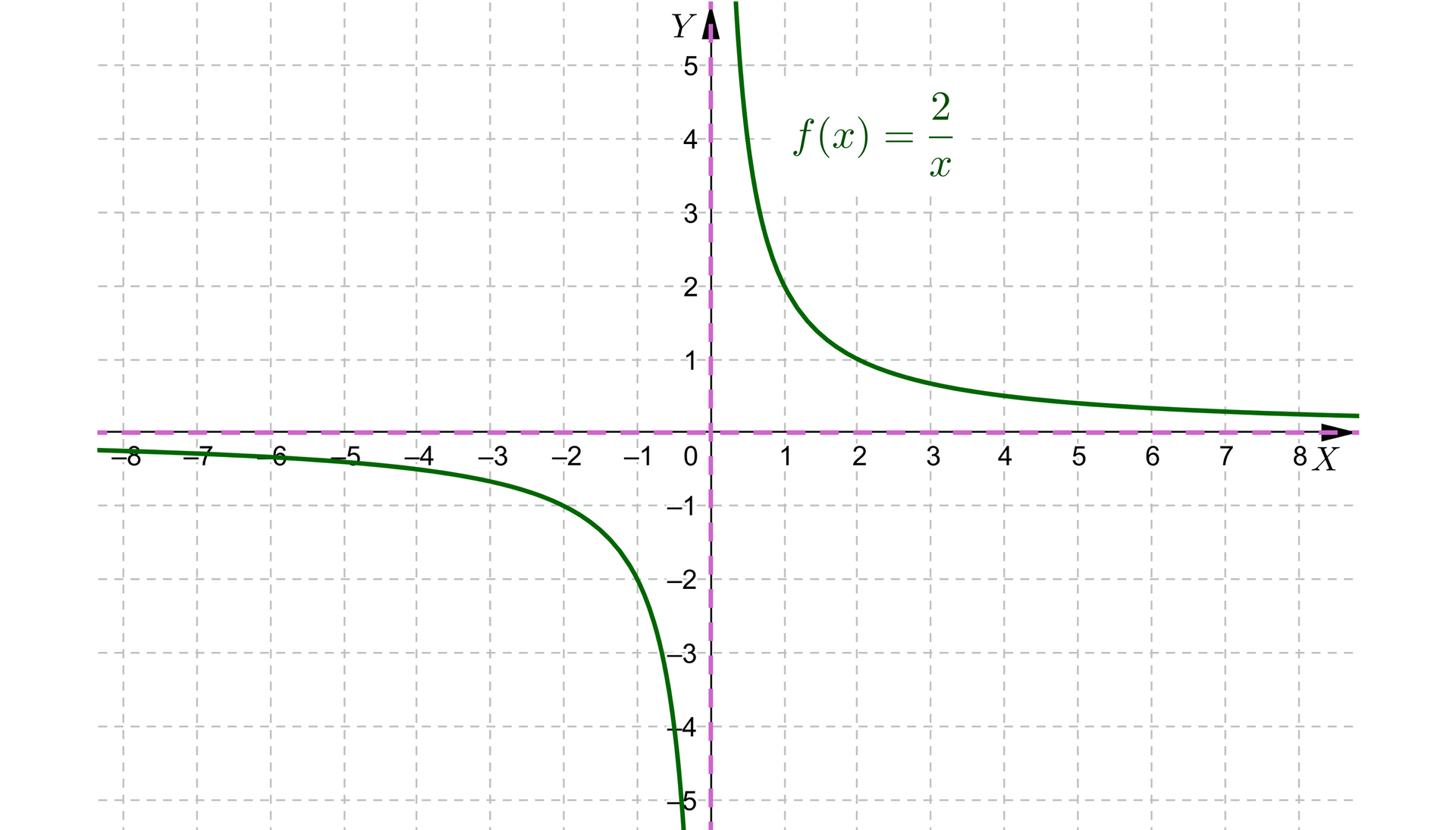
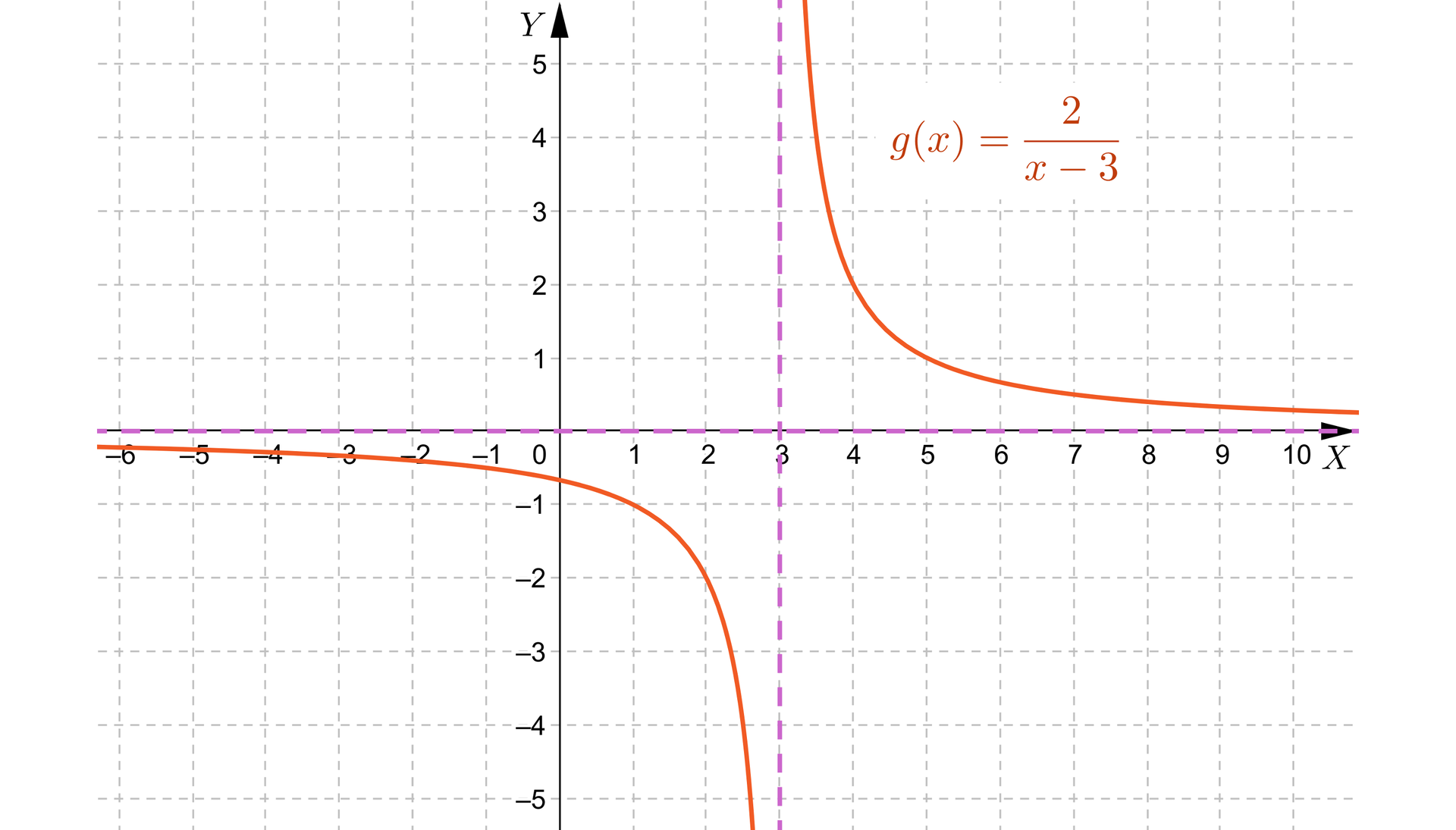
Przesuwając hiperbolę , gdzie , wzdłuż osi należy pamiętać, aby przesunąć w tym samym kierunku i o tyle samo jednostek asymptotę pionową wykresu funkcji.
Słownik
uporządkowana para liczb ; pierwszą współrzędną punktu nazywamy odciętą, zaś drugą rzędną punktu
zbiór argumentów funkcji
argument, czyli dla którego funkcja przyjmuje wartość ; mając wykres funkcji, jest to odcięta punktu przecięcia wykresu funkcji z osią