W graniastosłupie prawidłowym sześciokątnym wszystkie krawędzie są tej samej długości. Krótsza przekątna podstawy ma długość $12$. Obliczymy objętość tego graniastosłupa.

W sześciokącie foremnym krótsza przekątna ma długość $a\sqrt{3}$. A zatem $a\sqrt{3}=12$. I stąd $a=4\sqrt{3}$.

Ponieważ wszystkie krawędzie graniastosłupa są tej samej długości, to $H=4\sqrt{3}$.

Możemy już obliczyć objętość tego graniastosłupa: $V=6·\frac{{\left(4\sqrt{3}\right)}^2\sqrt{3}}{4}·4\sqrt{3}=864 {\mathrm{j}}^3$.

Obliczymy objętość graniastosłupa prawidłowego sześciokątnego, w którym dłuższa przekątna graniastosłupaprzekątna graniastosłupaprzekątna graniastosłupa ma długość $12$ i jest nachylona do płaszczyzny podstawy pod kątem $30°$.

Zróbmy rysunek pomocniczy:

RKy16C2EfcZrv

Ilustracja przedstawia graniastosłup prawidłowy sześciokątny. Wierzchołki dolnej podstawy są opisane: A, B, C, D, E oraz F. Wierzchołki górnej podstawy są opisane: G, H, I, J K oraz L. Punkty A, D, J tworzą trójkąt prostokątny. Którego jedna przyprostokątna to krawędź boczna graniastosłupa o długości x. Druga przyprostokątna to dłuższa przekątna sześciokąta o długości $\mathrm{x}\sqrt{3}$. Kąt DAJ pomiędzy dłuższą przyprostokątną a przeciwprostokątną wynosi 30 stopni. Przeciwprostokątna ma długość $2\mathrm{x}$.

Zależności pomiędzy bokami trójkąta na rysunku zostały na nim oznaczone.

Wiemy, że $2x=12$. Stąd $x=6$ i $x\sqrt{3}=6\sqrt{3}$.

A zatem $H=6$ i dłuższa przekątna podstawy $2a=6\sqrt{3}$. Stąd krawędź podstawy ma długość $a=3\sqrt{3}$. Możemy już policzyć objętość tego graniastosłupa.

Mamy więc $V=6·\frac{{\left(3\sqrt{3}\right)}^2\sqrt{3}}{4}·6=243\sqrt{3} {\mathrm{j}}^3$.

Oblicz długość dłuższej przekątnej graniastosłupa prawidłowego sześciokątnego o objętości $72$ i krawędzi podstawy $2$. Jaką miarę ma kąt nachylenia tej przekątnej do płaszczyzny podstawy?

Najpierw obliczymy długość wysokości graniastosłupa korzystając ze wzoru na objętość graniastosłupa.

Mamy $72=6·\frac{4\sqrt{3}}{4}H$. Czyli $12=\sqrt{3}H$, a stąd $H=4\sqrt{3}$.

Zróbmy rysunek pomocniczy:

R1CHgdP39h6U8

Ilustracja przedstawia graniastosłup prawidłowy sześciokątny. Jedna z krawędzi bocznych graniastosłupa wraz z dłuższą przekątną dolnej podstawy stanowią przyprostokątne trójkąta prostokątnego. Krawędź boczna ma długość $4\sqrt{3}$, przekątna podstawy ma długość cztery. Przeciwprostokątna jest podpisana literą p. Kąt pomiędzy przyprostokątną leżącą w płaszczyźnie podstawy a przeciwprostokątną jest podpisany literą alfa.

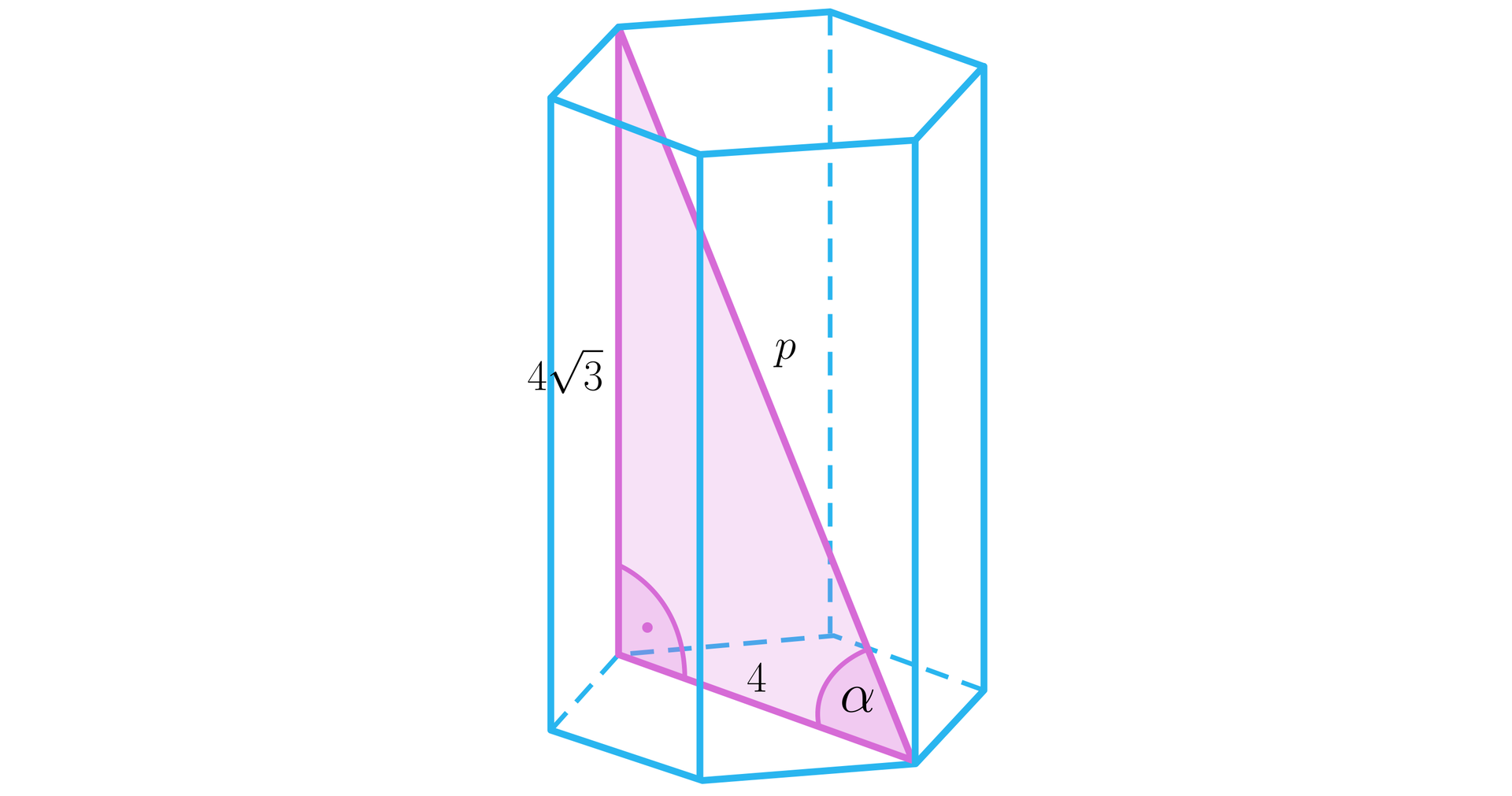
Z twierdzenia Pitagorasa mamy: ${\left(4\sqrt{3}\right)}^2+4^2=p^2$, a stąd $p^2=64$ i ostatecznie dłuższa przekątna graniastosłupaprzekątna graniastosłupaprzekątna graniastosłupa ma długość $p=8$.

Przyglądając się długościom boków trójkąta, z którego korzystaliśmy, widzimy, że jest to trójkąt prostokątny o kątach ostrych $30°$, $60°$. A zatem kąt nachylenia dłuższej przekątnej graniastosłupaprzekątna graniastosłupaprzekątnej graniastosłupa do płaszczyzny podstawy ma miarę $\alpha =60°$.

Kąt pomiędzy przekątnymi sąsiednich ścian bocznych w graniastosłupie prawidłowym sześciokątnymgraniastosłup prawidłowy sześciokątnygraniastosłupie prawidłowym sześciokątnym ma miarę $90°$. Oblicz pole powierzchni tego graniastosłupa wiedząc, że objętość wynosi $48\sqrt{6}$.

Zróbmy rysunek pomocniczy:

R15ExiTScHyqH

Ilustracja przedstawia graniastosłup prawidłowy sześciokątny. Wysokość graniastosłupa podpisano literą H. Krawędź podstawy sześciokąta podpisano literą a. Dwa wierzchołki górnej podstawy, będące końcami jej krótszej przekątnej oraz wierzchołek dolnej podstawy znajdujący się pomiędzy nimi tworzą trójkąt równoramienny, którego podstawa znajdująca się w płaszczyźnie górnej podstawy graniastosłupa ma długość $\mathrm{a}\sqrt{3}$. Każde z ramion trójkąta podpisano literą x.

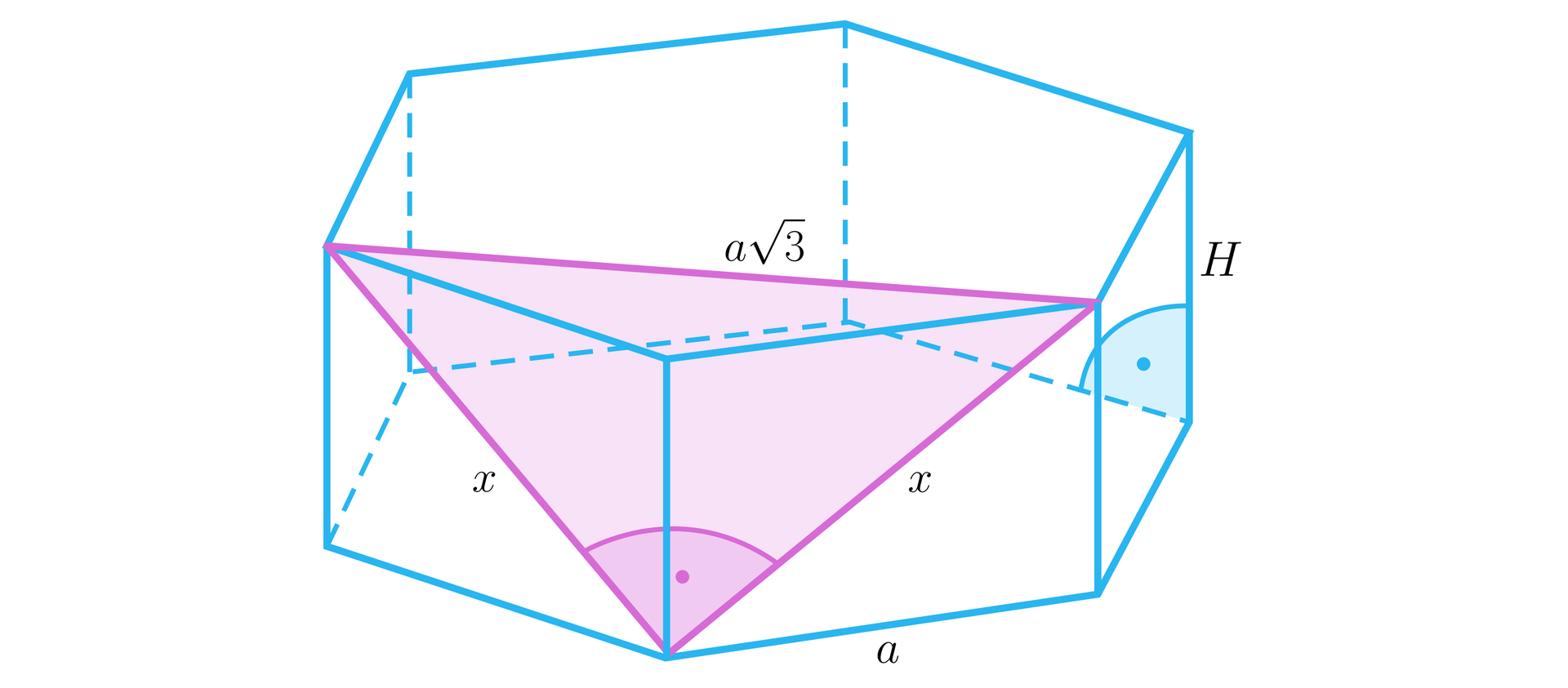
Trójkąt zaznaczony na rysunku jest równoramienny i prostokątny. Czyli $a\sqrt{3}=x\sqrt{2}$. Z twierdzenia Pitagorasa $x=\sqrt{a^2+H^2}$. Czyli $a\sqrt{3}=\sqrt{2a^2+2H^2}$. Podnosząc wyrażenie stronami do kwadratu otrzymujemy $3a^2=2a^2+2H^2$. Czyli $a^2=2H^2$, a stąd $a=H\sqrt{2}$.

Podstawmy to do objętości graniastosłupa: $48\sqrt{6}=6·\frac{{\left(H\sqrt{2}\right)}^2·\sqrt{3}}{4}H$. A zatem $32\sqrt{6}=2\sqrt{3}{H}^3$. Mamy więc $H^3=\frac{32\sqrt{6}}{2\sqrt{3}}=16\sqrt{2}$. Stąd $H=2\sqrt{2}$ oraz $a=4$.

Możemy więc obliczyć już pole powierzchni tego graniastosłupa $P_c=12·\frac{16\sqrt{3}}{4}+6·4·2\sqrt{2}=48\left(\sqrt{3}+\sqrt{2}\right)$.

graniastosłup, którego podstawa jest sześciokątem foremnym, a ściany boczne są przystającymi prostokątami

odcinek, którego końce są wierzchołkami dwóch różnych podstaw graniastosłupa nie leżące na jednej ścianie bocznej