Funkcja $f\left(x\right)$ ma asymptotę pionową prawostronną w $x=a$ wtedy i tylko wtedy, gdy $\underset{x\to a^{+}}{\lim }f\left(x\right)=+\infty$ lub $\underset{x\to a^{+}}{\lim }f\left(x\right)=-\infty$.

Funkcja $f\left(x\right)$ ma asymptotę pionową lewostronną w $x=a$ wtedy i tylko wtedy, gdy $\underset{x\to a^{-}}{\lim }f\left(x\right)=+\infty$ lub $\underset{x\to a^{-}}{\lim }f\left(x\right)=-\infty$.

Funkcja $f\left(x\right)$ ma asymptotę ukośną lewostronną $y=ax+b$ wtedy i tylko wtedy, gdy $\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x}=a$ i $\underset{x\to -\infty }{\lim }\left(f\left(x\right)-ax\right)=b$.

Funkcja $f\left(x\right)$ ma asymptotę ukośną prawostronną $y=ax+b$ wtedy i tylko wtedy, gdy $\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}=a$ i $\underset{x\to +\infty }{\lim }\left(f\left(x\right)-ax\right)=b$.

Funkcja $f\left(x\right)$ ma asymptotę poziomą prawostronną $y=b$ wtedy i tylko wtedy, gdy $\underset{x\to +\infty }{\lim }f\left(x\right)=b$.

Funkcja $f\left(x\right)$ ma asymptotę poziomą lewostronną $y=b$ wtedy i tylko wtedy, gdy $\underset{x\to -\infty }{\lim }f\left(x\right)=b$.

Powyższe definicje wykraczają poza zakres tego tematu. Podjemy je jako ciekawostkę. Dla naszego wywodu możemy przyjąć poniższą definicję asymptoty.

Prosta jest asymptotą danej krzywej, jeśli dla punktu oddalającego się nieograniczenie wzdłuż krzywej odległość tego punktu od prostej dąży do zera. Asymptota funkcji to asymptota krzywej stanowiącej wykres funkcji.

Intuicyjnie można przyjąć, że asymptota wykresu funkcji, to prosta, do której wykres się zbliża, jeśli oddalamy się od początku układu współrzędnych.

Poniższy rysunek przedstawia wykres funkcji $f\left(x\right)=\frac{5}{x}$. Wyznaczymy równania asymptot.

RQ5ww45z5MxGY

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu, oraz z pionową osią Y, od minus sześciu do sześciu. Na płaszczyźnie narysowano hiperbolę o równaniu $y=\frac{5}{x}$, której gałęzie znajdują się w pierwszej i trzeciej ćwiartce układu współrzędnych.

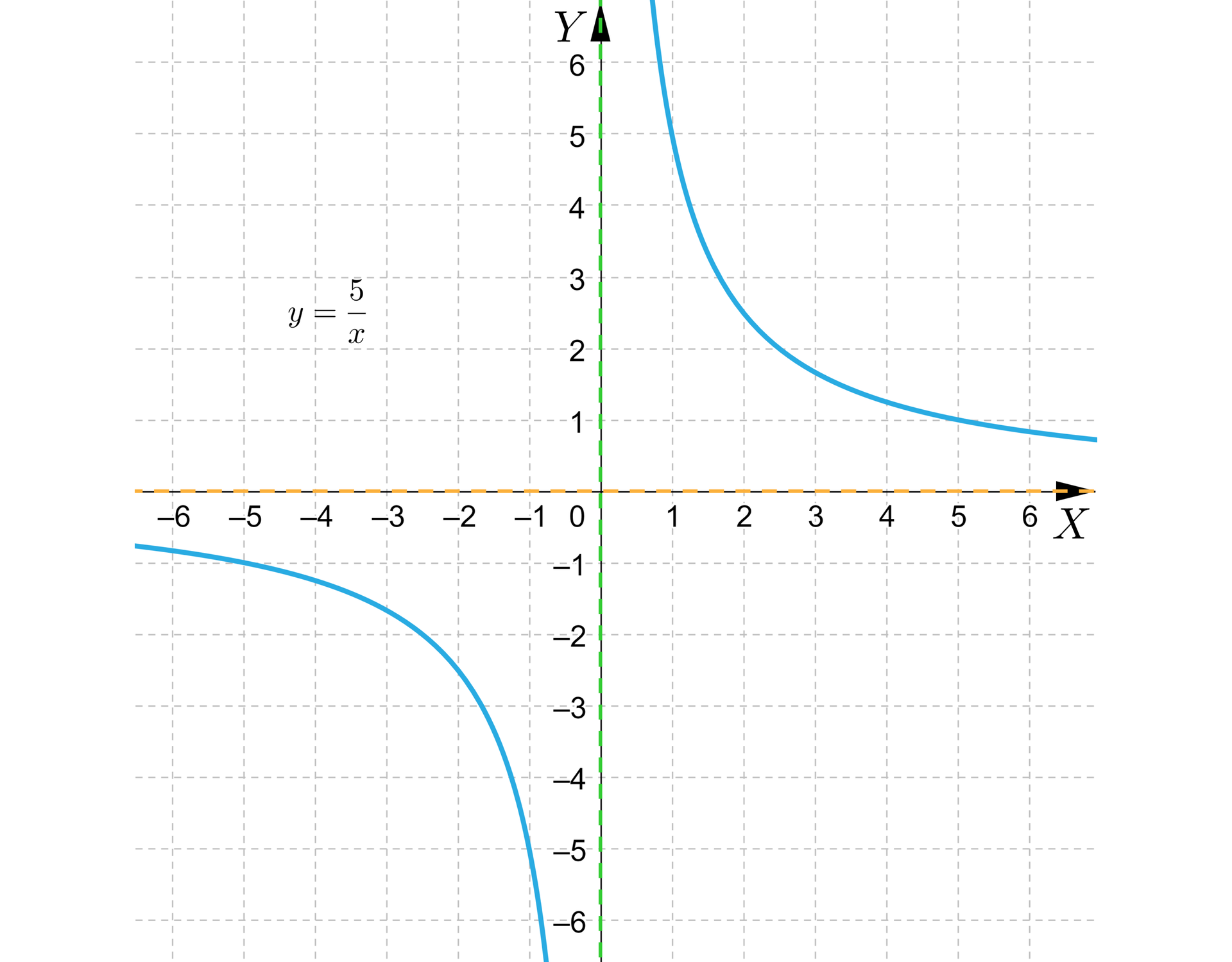
Rozwiązanie

Wykres funkcji posiada dwie asymptoty – pionową – o równaniu $x=0$ (zielona przerywana linia), oraz poziomą – o równaniu $y=0$ (żółta przerywana linia).

Poniższy rysunek przedstawia wykres funkcji $f\left(x\right)=-\frac{3}{x}$. Wyznaczymy równania asymptot.

R8NdLlKmo6gCb

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu, oraz z pionową osią Y, od minus sześciu do sześciu. Na płaszczyźnie narysowano hiperbolę o równaniu $y=\frac{-3}{x}$, której gałęzie znajdują się w pierwszej i trzeciej ćwiartce układu współrzędnych i zmierzają do zera.

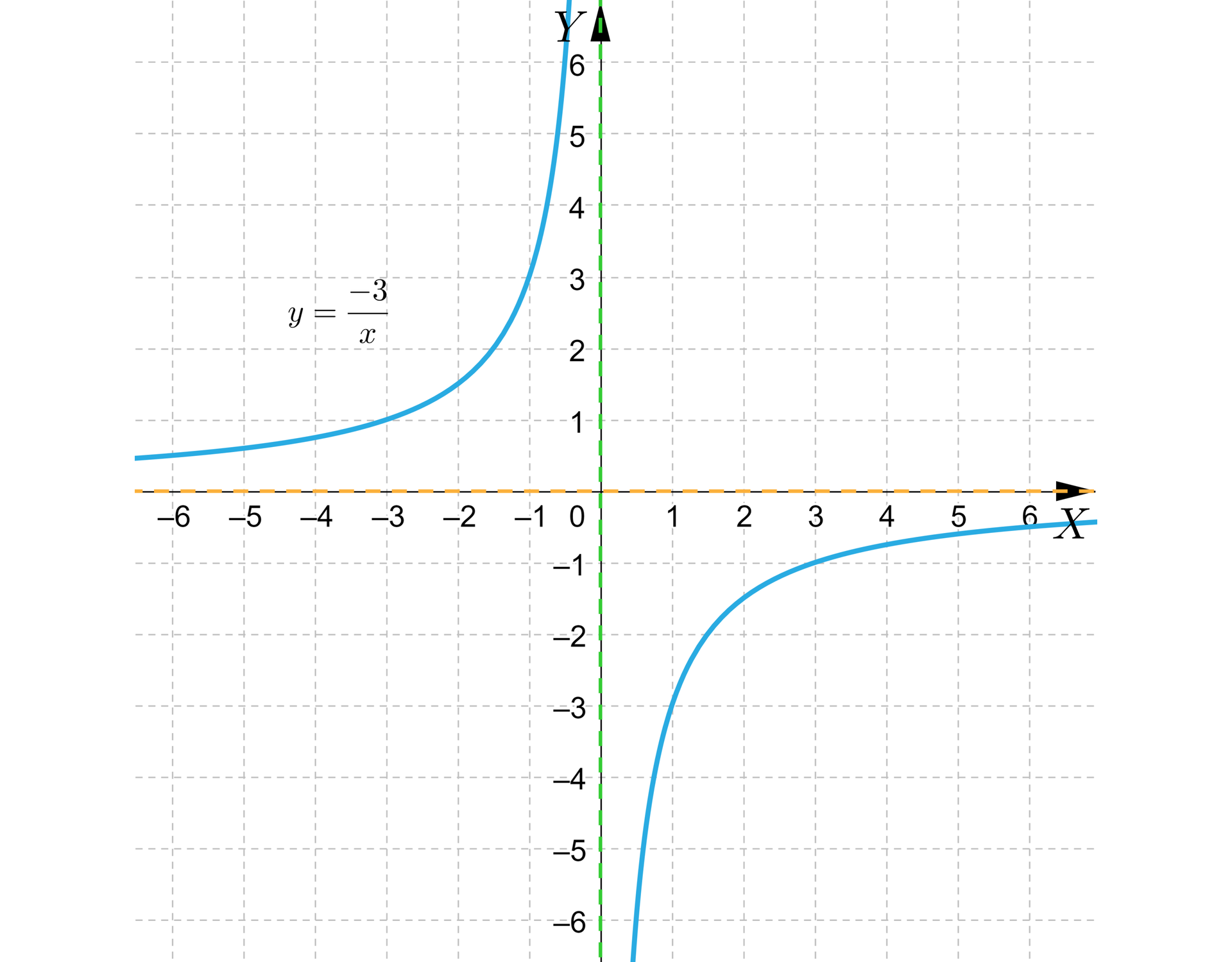
Rozwiązanie

Wykres funkcji posiada dwie asymptoty – pionową – o równaniu $x=0$ (zielona przerywana linia), oraz poziomą – o równaniu $y=0$ (żółta przerywana linia).

Wyznaczymy dziedzinę i zbiór wartości funkcji $f\left(x\right)=\frac{a}{x}$, $a\ne 0$.

Rozwiązanie

$D_f=\mathrm{ℝ}\setminus \left\{0\right\}$

$Z{W}_f=\mathrm{ℝ}\setminus \left\{0\right\}$

Zauważmy, że funkcja nie jest określona dla $x=0$ i właśnie prosta o równaniu $x=0$ jest asymptotą pionową. Podobnie funkcja nie przyjmuje wartości $y=0$ i prosta $y=0$ jest asymptotą poziomą.

Wyznaczymy równania asymptot wykresu funkcji $f\left(x\right)=\frac{2}{x-1}$.

Rozwiązanie

Wykres funkcji $f\left(x\right)=\frac{2}{x-1}$ powstaje w wyniku translacjitranslacjatranslacji wykresu funkcji $g\left(x\right)=\frac{2}{x}$ o wektor $\overrightarrow{v}=\left[1,0\right]$. Przesunięciu ulegają również asymptoty. Zauważmy, że równanie asymptoty poziomej nie zmieni się, natomiast asymptota pionowa będzie miała inne równanie.

Odpowiedź:

Równanie asymptoty pionowej: $x=1$

Równanie asymptoty poziomej: $y=0$

Poniższy rysunek przedstawia opisaną sytuację.

RmGvjvVgx5tDK

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do pięciu, oraz z pionową osią Y, od minus sześciu do sześciu. Na płaszczyźnie narysowano dwa wykresy funkcji. Wykres funkcji $y=\frac{2}{x}$ ma asymptotę pionową o równaniu $x=0$, oraz poziomą $y=0$. Gałęzie hiperboli znajdują się w pierwszej oraz trzeciej ćwiartce układu współrzędnych. Wykres funkcji $y=\frac{2}{x-1}$, stanowi przesunięcie pierwszego wykresu o jedną jednostkę w prawo. Stąd, asymptota pionowa funkcji ma równanie $x=1$. Wykres leży w pierwszej, trzeciej, oraz czwartej ćwiartce układu współrzędnych.

Zauważmy, że zmianie uległa dziedzina funkcji, tzn. $D_f=\mathrm{ℝ}\setminus \left\{1\right\}$, oraz przedziały monotoniczności funkcji, funkcja jest malejąca w każdym z przedziałów: $\left(-\infty ,1\right)$, $\left(1,\infty \right)$.

Wyznaczymy równania asymptot wykresu funkcji $f\left(x\right)=-\frac{1}{x}-2$.

Rozwiązanie

Wykres funkcji $f\left(x\right)=-\frac{1}{x}-2$ powstaje w wyniku przesunięcia wykresu funkcji $g\left(x\right)=\frac{-1}{x}$ o wektor $\overrightarrow{v}=\left[0,-2\right]$. Przesunięciu ulegają również asymptoty. Zauważmy, że równanie asymptoty pionowej nie zmieni się, natomiast asymptota pozioma będzie miała inne równanie.

Odpowiedź:

Równanie asymptoty pionowej: $x=0$

Równanie asymptoty poziomej: $y=-2$

Poniższy rysunek przedstawia opisaną sytuację.

R1CHejlpTZRMA

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu, oraz z pionową osią Y od minus pięciu do czterech. Na płaszczyźnie narysowano wykresy dwóch funkcji. Wykres funkcji $y=-\frac{1}{x}$ ma asymptotę ma asymptotę pionową o równianiu $x=0$, oraz poziomą $y=0$. Gałęzie hiperboli znajdują się w drugiej oraz czwartej ćwiartce układu współrzędnych. Wykres funkcji $y=-\frac{1}{x}-2$, stanowi przesunięcie wykresu pierwszego o dwie jednostki w dół. Stąd asymptota pozioma funkcji ma równanie $y=-2$. Wykres po przesunięciu znajduje się w drugiej, trzeciej, oraz czwartej ćwiartce układu współrzędnych.

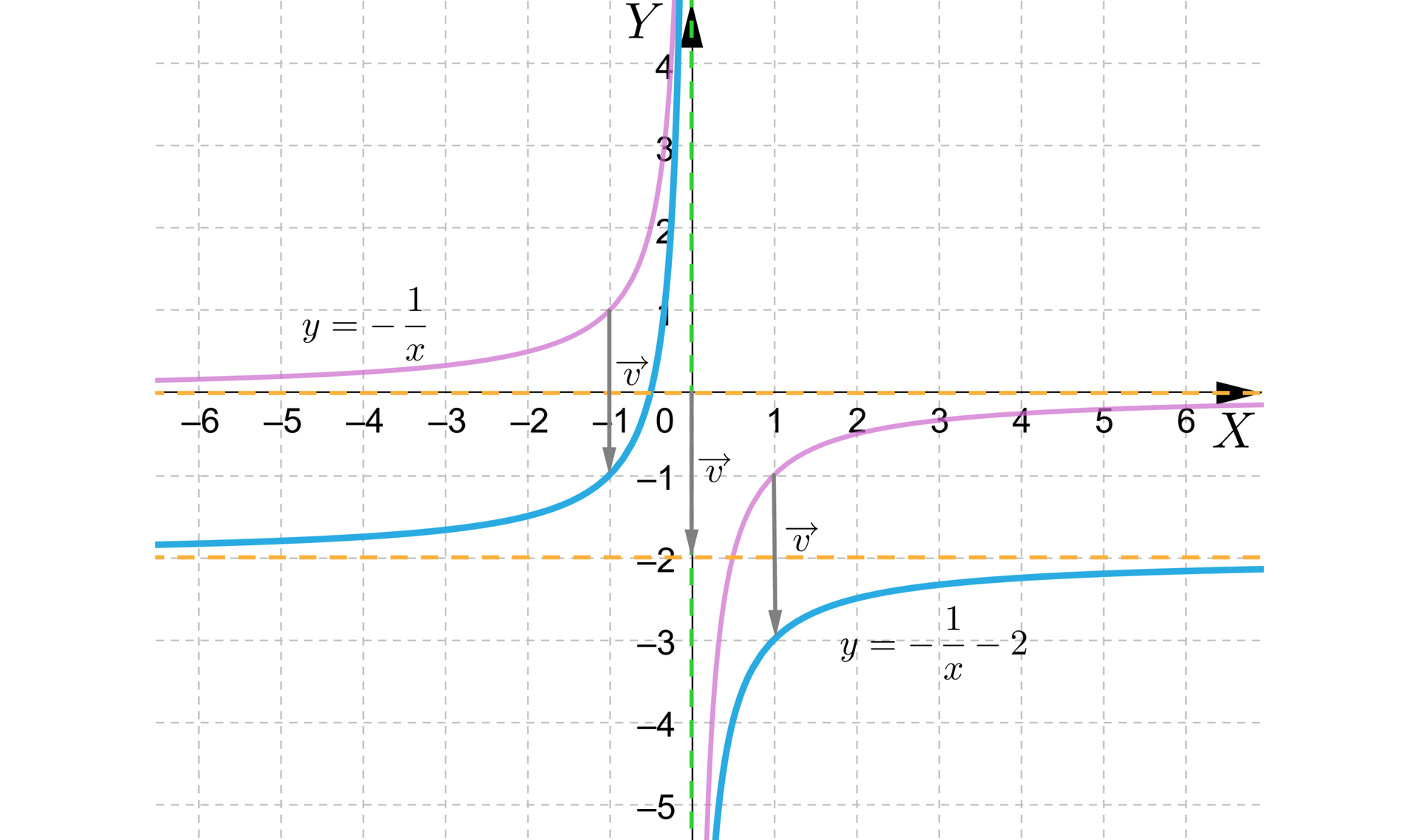
Zauważmy, że zmianie uległ zbiór wartości funkcji, tzn. $Z{W}_f=\mathrm{ℝ}\setminus \left\{-2\right\}$.

Wyznaczymy równania asymptot wykresu funkcji $f\left(x\right)=\frac{3}{x+2}+4$.

Rozwiązanie

Wykres funkcji $f\left(x\right)=\frac{3}{x+2}+4$ powstaje w wyniku translacji wykresu funkcji $g\left(x\right)=\frac{3}{x}$ o wektor $\overrightarrow{u}=\left[-2,4\right]$. Przesunięciu ulegają również asymptoty.

Odpowiedź:

Równanie asymptoty pionowej: $x=-2$

Równanie asymptoty poziomej: $y=4$

Poniższy rysunek przedstawia opisaną sytuację.

RIEMFzTKobSkF

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu, oraz z pionową osią Y od minus trzech do sześciu. Na płaszczyźnie narysowano wykresy dwóch funkcji. Wykres funkcji $y=\frac{3}{x}$ to hiperbola, której gałęzie znajdują się w pierwszej oraz trzeciej ćwiartce układu współrzędnych. Asymptotę pionową tego wykresu opisuje równanie $x=0$, natomiast asymptotę poziomą $y=0$. Wykres funkcji $y=\frac{3}{x+2}+4$ stanowi przesunięcie wykresu pierwszego o dwie jednostki w lewo, oraz cztery jednostki w górę. Stąd asymptotę pionową tego wykresu opisuje równanie $x=-2$, natomiast asymptotę poziomą $y=4$.

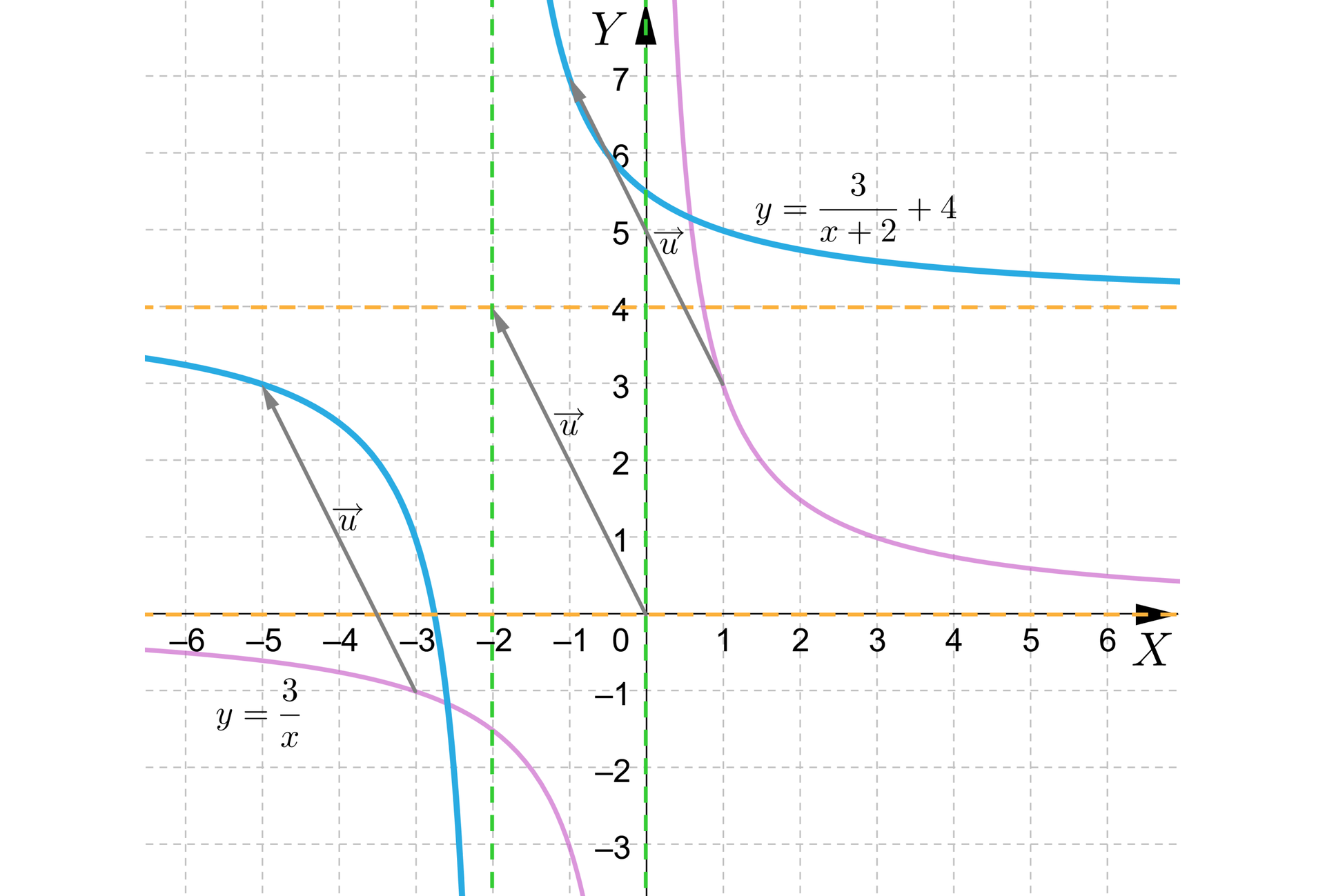
Zauważmy, że wraz z przesunięciem wykresu funkcji zmianie uległa dziedzina i zbiór wartości funkcji, więc i asymptoty.

$D_f=\mathrm{ℝ}\setminus \left\{-2\right\}$

$Z{W}_f=\mathrm{ℝ}\setminus \left\{4\right\}$

przesunięcie każdego punktu figury bądź przestrzeni o tę samą odległość w ustalonym kierunku