Rozpatrzmy teraz dwa ostrosłupy prawidłowe czworokątne o krawędziach podstawy długości $10$ i $5$ i wysokościach odpowiednio $8$ i $4$.

R1Y3c2su1CeTY

Ilustracja przedstawia dwa ostrosłupy prawidłowe czworokątne. Większy z nich ma krawędź podstawy długości 10. Natomiast wysokość upuszczona na spodek wysokości, leżący na przecięciu przekątnych kwadratu w podstawie ma długość 8. W mniejszym ostrosłupie krawędź podstawy wynosi 8, a wysokość 4.

Są to bryły podobnefigury podobnebryły podobne. Skala podobieństwa większej z nich do mniejszej wynosi $k=\frac{10}{5}=2$.

Policzmy ich objętości.

$V_1=\frac{1}{3}·{10}^2·8=\frac{800}{3}$

$V_2=\frac{1}{3}·5^2·4=\frac{100}{3}$

Ich stosunek wynosi więc: $\frac{V_1}{V_2}=\frac{\frac{800}{3}}{\frac{100}{3}}=8=2^3=k^3$.

Jeśli skala podobieństwa brył podobnych jest równa $k$, to stosunek ich objętości jest równy $k^3$.

Dane są dwie kule. Objętość pierwszej jest równa $V$, a druga ma promień $3$ razy dłuższy od promienia pierwszej kuli. Obliczmy objętość drugiej kuli.

Rozwiązanie:

Dwie kule są podobne. Ich skala podobieństwa wynosi $k=3$. Zatem stosunek ich objętości wynosi $k^3=27$. Objętość drugiej kuli wynosi więc $27V$.

Uzasadnijmy, że stożek o wysokości długości $6 \mathrm{cm}$ i polu powierzchni całkowitej $144\pi$ nie jest podobny do stożka o tworzącej długości $20 \mathrm{cm}$ i objętości $1000\pi$.

Rozwiązanie:

Rozważmy dwa stożki.

Niech $r_1$– długość promienia pierwszego stożka, $l_1$– długość tworzącej pierwszego stożka. Wówczas otrzymujemy równanie:

$6^2+r_1^2=l_1^2$

$r_1^2=l_1^2-36$

$r_1=\sqrt{l_1^2-36}$

Wiemy, że pole tego stożka wynosi $144\pi$, więc

$144\pi =\pi r_1^2+\pi r_1{l}_1$

$144\pi =\pi \left(l_1^2-36\right)+\pi \left(\sqrt{l_1^2-36}\right)l_1\mid :\pi$

$144=l_1^2-36+l_1\sqrt{l_1^2-36}$

$180-l_1^2={\left.l_1\sqrt{l_1^2-36}\right|}^2$

$32400-360l_1^2+l_1^4=l_1^2\left(l_1^2-36\right)$

$32400=324l_1^2$

$l_1^2=100$

$l_1=10$

Zatem

$r_1=\sqrt{100-36}=8$

$V=\frac{1}{3}\pi ·8^2·6=128\pi {\mathrm{cm}}^3$

Porównajmy tworzące naszych stożków:

$\frac{10}{20}=\frac{1}{2}$

${\left(\frac{1}{2}\right)}^3=\frac{1}{8}$

Zatem objętość pierwszego stożka powinna być mniejsza $8$ razy od objętości drugiego stożka. Sprawdźmy to:

$\frac{1000\pi }{8}=125\pi \ne 128\pi$

Oznacza to, że stożki nie są podobnefigury podobnepodobne.

Stożek o objętości $V$ przecięto płaszczyzną równoległą do podstawy. Płaszczyzna podzieliła wysokość stożka w stosunku $3:8$, licząc od wierzchołka. Obliczymy objętości brył powstałych w wyniku tego podziału.

Rozwiązanie:

Wykonajmy rysunek pomocniczy:

RziuQI4cnx4iL

Ilustracja przedstawia stożek ABS. Na lewym ramieniu zaznaczono punkt $A\text{'}$, a na prawym $B\text{'}$, które następnie połączono i stworzono płaszczyznę równoległą do podstawy. Z wierzchołka S upuszczona została wysokość stożka, którą nasza płaszczyzna podzieliła w stosunku $3 : 8$. Wysokość małego stożka oznaczono jako 3x, a dużego, ściętego 8x.

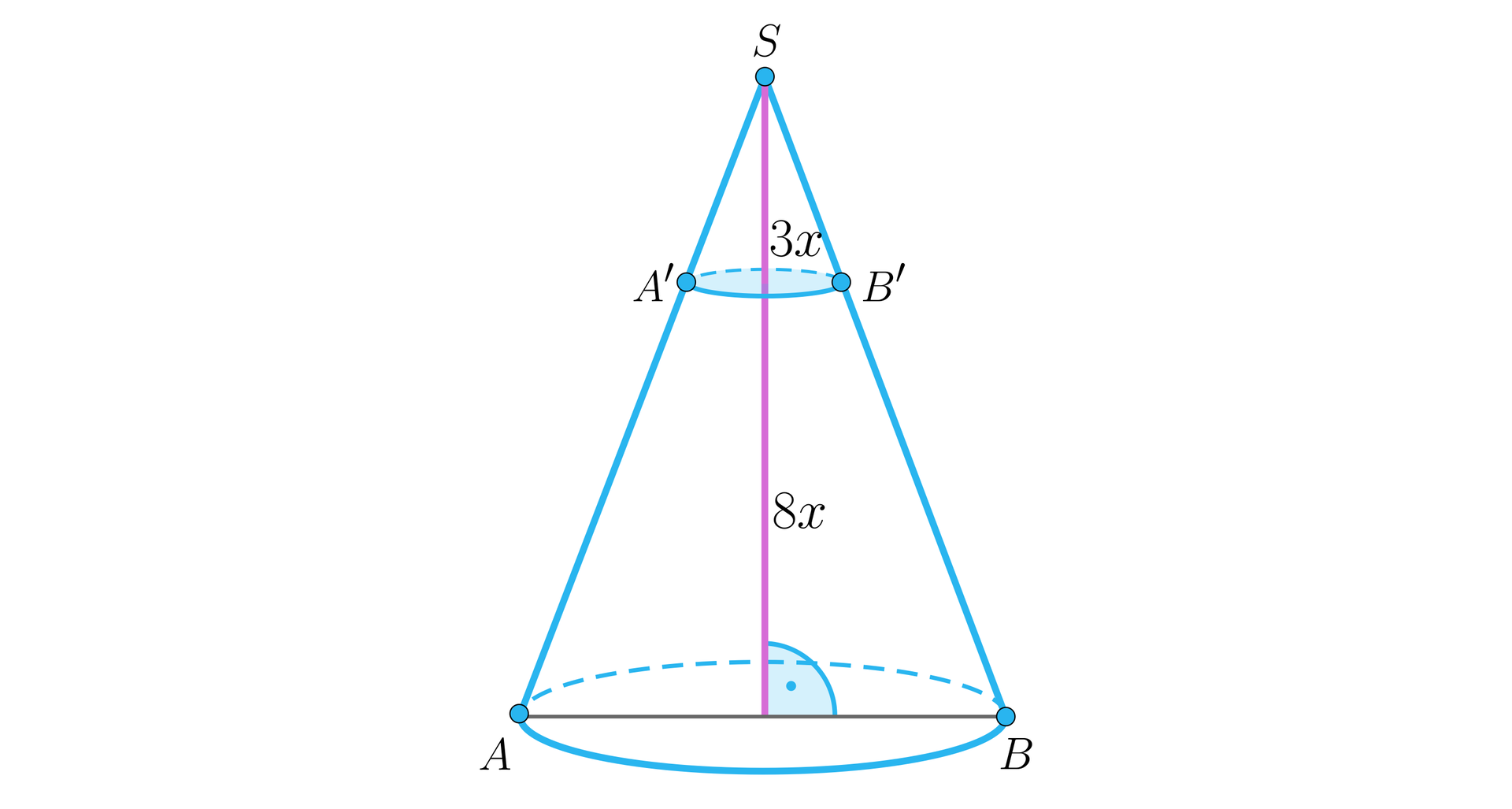
Trójkąty $ABS$ i $A^{\text{'}}{B}^{\text{'}}S$ są podobne $\left(KKK\right)$. Skala ich podobieństwa wynosi $\frac{3}{11}$.

Zatem stożki są podobne w tej samej skali.

Stosunek ich objętości wynosi więc ${\left(\frac{3}{11}\right)}^3=\frac{27}{1331}$.

Objętość małego stożka wynosi $\frac{27}{1331}V$, objętość stożka ściętego wynosi

$V-\frac{27}{1331}V=\frac{1304}{1331}V$

Bryły powstałe w wyniku podziału mają więc objętości równe $\frac{27}{1331}V$ i $\frac{1304}{1331}V$.

Ostrosłup przecięto płaszczyzną równoległą do podstawy. Oblicz stosunek objętości otrzymanych brył, wiedząc, że pole przekroju stanowi $49\%$ pola podstawy ostrosłupa.

Rozwiązanie:

Wykonajmy rysunek pomocniczy:

R1TFl5p2W7zne

Ilustracja przedstawia ostrosłup czworokątny ABCDS. Z wierzchołka S upuszczona została wysokość padająca na spodek wysokości, leżący na przecięciu przekątnych podstawy. Na krawędziach bocznych zaznaczono punkty $A\text{'}$, $B\text{'}$, $C\text{'}$ oraz $D\text{'}$, które połączono i stworzono płaszczyznę równoległą do podstawy.

Niech $P$– pole podstawy ostrosłupa, $H$- wysokość ostrosłupa. Wówczas pole przekroju $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ wynosi $0,49 P$.

Jako $k$ oznaczmy skalę podobieństwa ostrosłupów $ABCDS$ i $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}S$.

Stosunek pól ich podstaw wynosi $k^2$. Zatem mamy:

$k^2=\frac{0,49P}{P}$

$k=0,7$

Objętość wyjściowego ostrosłupa wynosi $V=\frac{1}{3}P·H$. Objętość ostrosłupa $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}S$ wynosi zatem:

$V_1={\left(0,7\right)}^{3}V=\frac{343}{3000}PH$.

Objętość pozostałej części bryły wynosi więc:

$V_2=V-V_1=\frac{1}{3}PH-\frac{343}{3000}PH=\frac{1000}{3000}PH-\frac{343}{3000}PH=\frac{657}{3000}PH$

Stosunek objętości otrzymanych brył wynosi zatem:

$\frac{V_1}{V_2}=\frac{\frac{343}{3000}PH}{\frac{657}{3000}PH}=\frac{343}{657}$.

Pola podstaw stożka ściętego wynoszą $P$ i $S$, jego wysokość wynosi zaś $h$. Wykażmy, że objętość tej bryły wynosi $V=\frac{1}{3}h\left(P+\sqrt{PS}+S\right)$.

Rozwiązanie:

Wykonajmy rysunek pomocniczy. Stożek ścięty powstał poprzez przecięcie stożka $ABS$ płaszczyzną równoległą do podstawy.

Oznaczmy jako $x$ wysokość stożka $A^{\text{'}}{B}^{\text{'}}S$.

R1PRBBBel1Le5

Ilustracja przedstawia stożek ścięty powstały poprzez przecięcie stożka ABS płaszczyzną $A\text{'}B\text{'}$, równoległą do podstawy. Wysokość stożka $A\text{'}B\text{'}S$ oznaczono jako x, a wysokość ściętego stożka jako h.

Niech $P$- pole górnej podstawy, $S$- pole dolnej podstawy.

Stożki $ABS$ i $A^{\text{'}}{B}^{\text{'}}S$ są podobne. Skalę ich podobieństwa oznaczmy jako $k$. Wówczas:

$k^2=\frac{P}{S}$

$k=\sqrt{\frac{P}{S}}$

Oznaczmy jako $r$ - promień stożka $A^{\text{'}}{B}^{\text{'}}S$, a $R$ - promień stożka $ABS$.

Wiemy, że $\pi r^2=P$, czyli $r=\sqrt{\frac{P}{\pi }}$ oraz $\pi R^2=S$, co daje, że $R=\sqrt{\frac{S}{\pi }}$. Z podobieństwa brył powstaje proporcja:

$\frac{x}{r}=\frac{x+h}{R}$

$\frac{x}{\sqrt{\frac{P}{\pi }}}=\frac{x+h}{\sqrt{\frac{S}{\pi }}}$

$x\sqrt{\frac{S}{\pi }}=x\sqrt{\frac{P}{\pi }}+h\sqrt{\frac{P}{\pi }}$

$x\left(\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}\right)=h\sqrt{\frac{P}{\pi }}$

$x=\frac{h\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}$

$x+h=\frac{h\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}+\frac{h\sqrt{\frac{S}{\pi }}-h\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}=\frac{h\sqrt{\frac{S}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}$

Obliczmy objętości naszych stożków.

Objętość stożka $ABS$:

$V=\frac{1}{3}·S·\frac{h\sqrt{\frac{S}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}$

Objętość stożka $A^{\text{'}}{B}^{\text{'}}S$:

$V_1=\frac{1}{3}·P·\frac{h\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}$

Zatem objętość stożka ściętego wynosi:

$V_2=V-V_1=\frac{1}{3}·S·\frac{h\sqrt{\frac{S}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}-\frac{1}{3}·P·\frac{h\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}=$$=\frac{1}{3}h\left(\frac{S\sqrt{\frac{S}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}-\frac{P\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}\right)=\frac{1}{3}h·\frac{S\sqrt{\frac{S}{\pi }}-P\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}$

Usuńmy niewymierność z mianownika:

$\begin{array}{l}\frac{1}{3}h·\frac{S\sqrt{\frac{S}{\pi }}-P\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}-\sqrt{\frac{P}{\pi }}}·\frac{\sqrt{\frac{S}{\pi }}+\sqrt{\frac{P}{\pi }}}{\sqrt{\frac{S}{\pi }}+\sqrt{\frac{P}{\pi }}}=\frac{1}{3}h\left(\frac{S·\frac{S}{\pi }+S\sqrt{\frac{SP}{{\pi }^2}}-P\sqrt{\frac{SP}{{\pi }^2}}-P·\frac{P}{\pi }}{\frac{S}{\pi }-\frac{P}{\pi }}\right)=\\ =\frac{1}{3}h\left(\frac{S^2+S\sqrt{SP}-P\sqrt{SP}-P^2}{S-P}\right)=\frac{1}{3}h\frac{\left(S-P\right)\left(S+P\right)+\sqrt{SP}\left(S-P\right)}{S-P}=\\ =\frac{1}{3}h\left(S+P+\sqrt{SP}\right)=\frac{1}{3}h\left(P+\sqrt{PS}+S\right)\end{array}$

jeżeli dane są cztery odcinki $a$, $b$, $c$, $d$ takie, że stosunek pierwszych dwóch $\left(a:b\right)$ jest równy stosunkowi dwóch ostatnich $\left(c:d\right)$, to takie odcinki nazywamy proporcjonalnymi i wyrażamy to, pisząc proporcję $a:b=c:d$;
w uproszczeniu możemy powiedzieć, że ich iloraz jest stały

figury, których stosunek długości każdej pary odpowiadających sobie odcinków jest stały