Przeczytaj
Jeżeli podstawą ostrosłupa jest wielokąt foremny np. trójkąt równoboczny a spodek wysokości ostrosłupaspodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na jego podstawie, to mówimy, że taki ostrosłup jest prawidłowy.
Ostrosłup prawidłowy trójkątny, to taki ostrosłup prosty, którego podstawą jest trójkąt foremny, czyli trójkąt równoboczny. Spodek wysokości jest punktem przecięcia się środkowych, które są zarazem wysokościami i dwusiecznymi. Ściany boczne ostrosłupa są przystającymi trójkątami równoramiennymi o wspólnym wierzchołku zwanym wierzchołkiem ostrosłupa.
Objętość ostrosłupa prawidłowego trójkątnego wyraża się za pomocą wzoru:
czyli
po podstawieniu za , gdzie:
– oznacza pole podstawy ostrosłupa, czyli trójkąta równobocznego,
– wysokość bryły.
Dla czworościanu foremnegoczworościanu foremnego o krawędzi objętość
Ważne twierdzenia
Jeżeli ostrosłup jest prawidłowy, to:
wszystkie jego krawędzie boczne są równe i nachylone pod tym samym kątem do podstawy,
jego ściany boczne są przystającymi trójkątami równoramiennymi,
kąty dwuścienne nachylenia jego ścian bocznych do podstawy są równe,
kąty dwuścienne między jego sąsiednimi ścianami są równe.
Jeżeli podstawą ostrosłupa jest wielokąt foremny i wszystkie krawędzie boczne są równe, to ostrosłup ten jest prawidłowy.
Jeżeli podstawą ostrosłupa jest wielokąt foremny i wszystkie krawędzie boczne są nachylone do płaszczyzny podstawy pod tym samym kątem, to ostrosłup ten jest prawidłowy.
Obliczmy objętość ostrosłupa prawidłowego trójkątnego, którego wysokość jest równa , a krawędź boczna .
Rozwiązanie
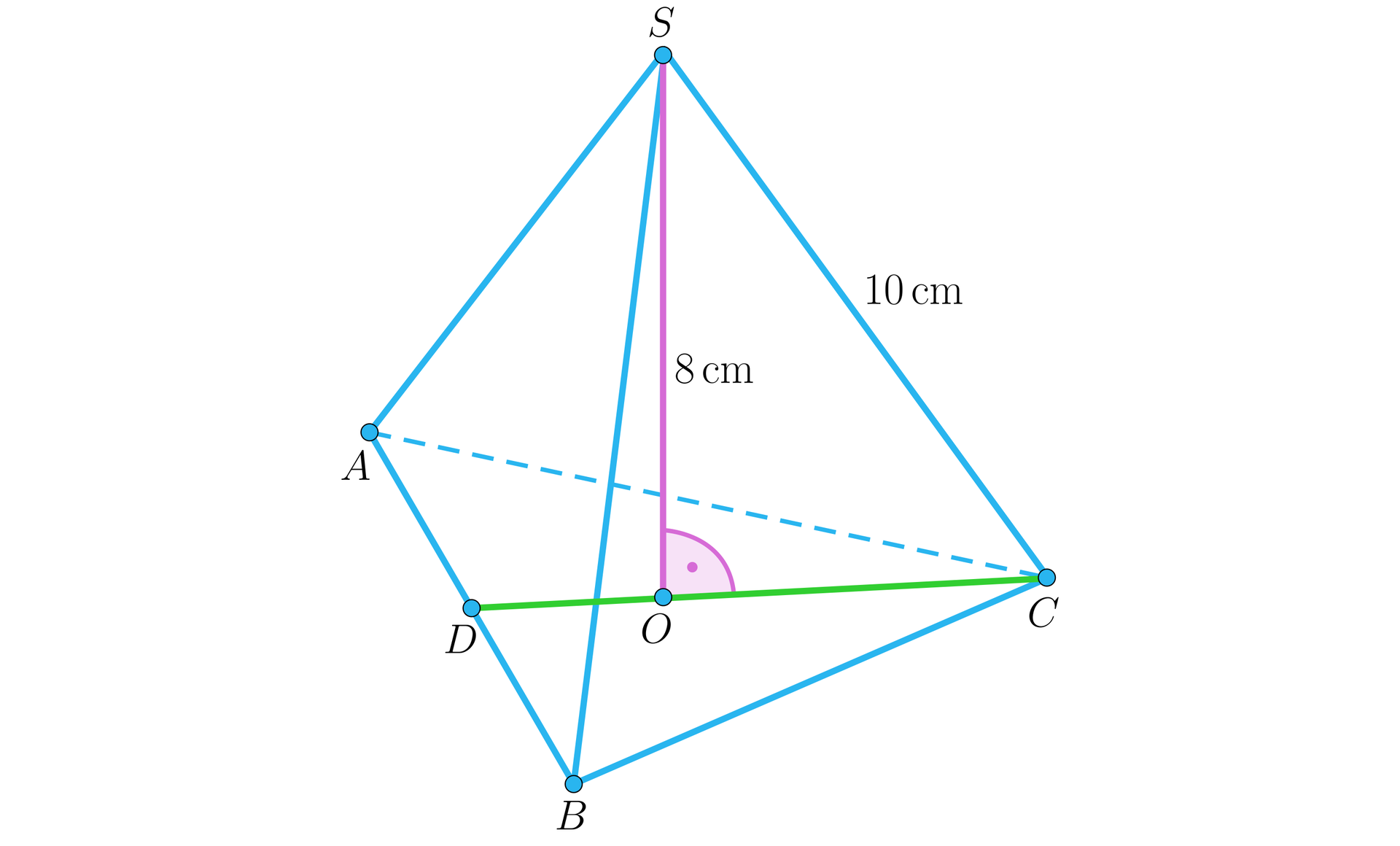
Przyjmujemy, że oraz , wówczas: .
Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie, zatem:
.
Rozpatrujemy trójkąt prostokątny , na podstawie twierdzenia Pitagorasa mamy:
Obliczamy pole podstawy ostrosłupa:
.
Zatem objętość ostrosłupa:
.
Obliczmy objętość ostrosłupa prawidłowego trójkątnego, którego wysokość jest równa i tworzy:
a) z krawędzią boczną kąt taki, że ,
b) z wysokością ściany bocznej kąt taki, że .
Rozwiązanie
a) Wykonajmy rysunek z odpowiednimi oznaczeniami, zaznaczamy kąt miedzy wysokością ostrosłupa a krawędzią boczną.
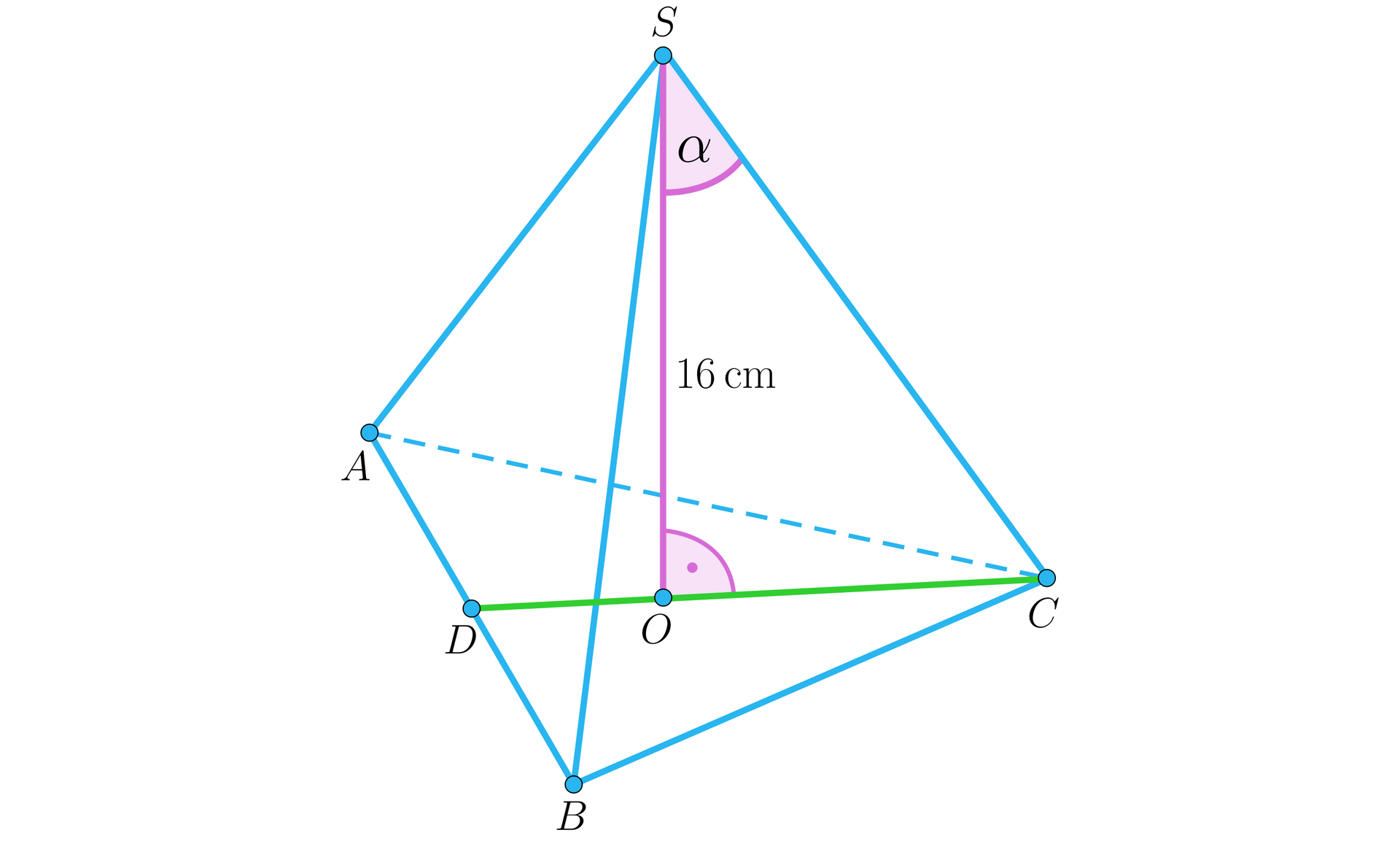
Przyjmujemy, że oraz , wówczas: .
Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie, zatem:
.
W trójkącie mamy: , więc , stąd , to .
Obliczamy pole podstawy ostrosłupa:
.
Zatem objętość ostrosłupa:
.
b) Wykonajmy rysunek z odpowiednimi oznaczeniami, zaznaczamy kąt między wysokością ostrosłupa a wysokością ściany bocznej.
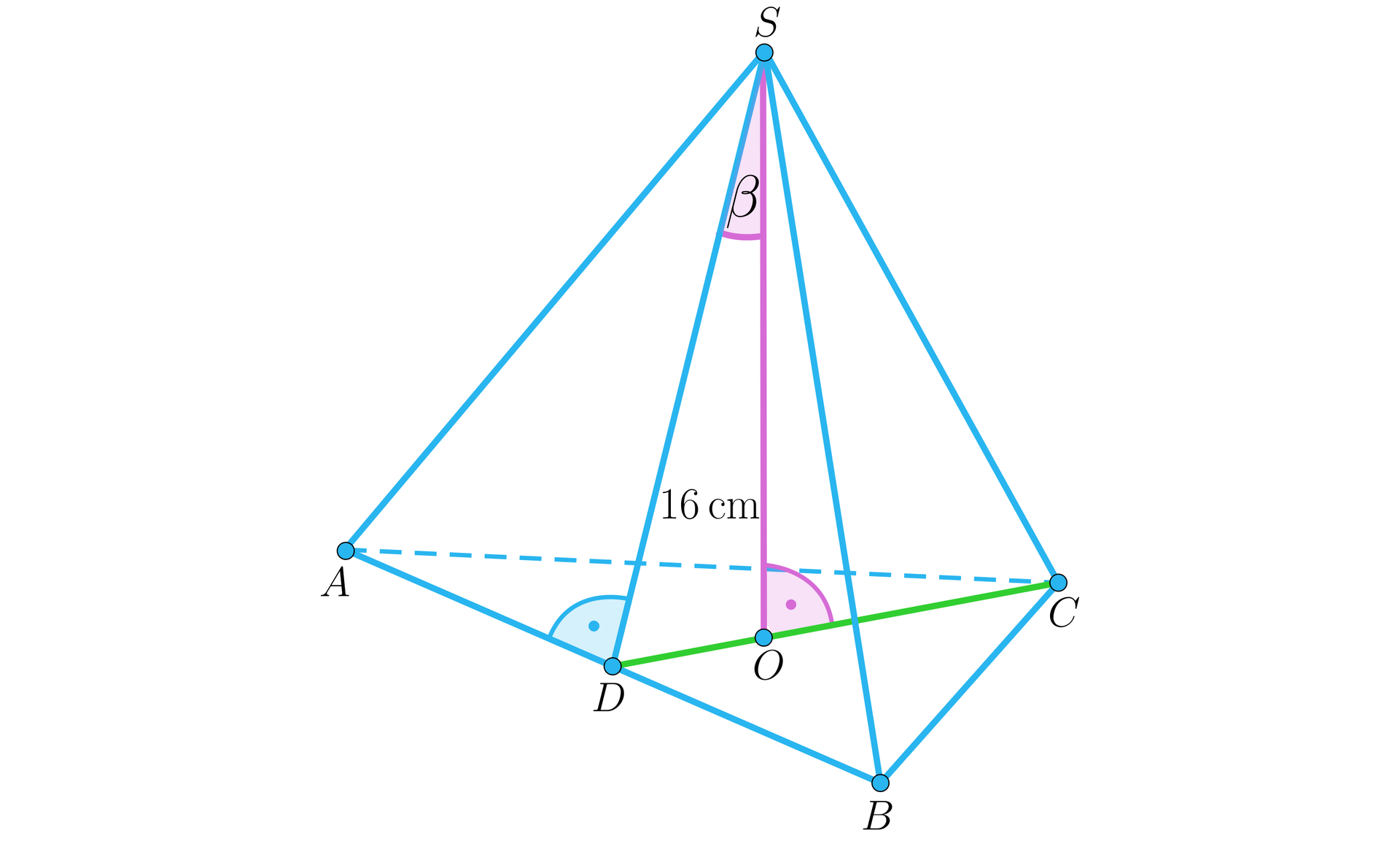
Przyjmujemy, że oraz , wówczas: .
Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie, zatem:
.
W trójkącie mamy: , więc , stąd .
Korzystając z twierdzenia Pitagorasa mamy:
.
Obliczamy pole podstawy ostrosłupa:
.
Zatem objętość ostrosłupa:
.
Przekrój ostrosłupa prawidłowego trójkątnego płaszczyzną przechodzącą przez wierzchołek i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość . Obliczymy objętość tego ostrosłupa.
Rozwiązanie

Oznaczamy , wtedy , bo przekrój jest trójkątem równobocznym oraz .
Rozpatrujemy trójkąt prostokątny , na podstawie twierdzenia Pitagorasa mamy:
.
Rozpatrujemy trójkąt prostokątny , na podstawie twierdzenia Pitagorasa mamy:
.
Obliczamy pole podstawy ostrosłupa:
.
Zatem objętość ostrosłupa:
.
W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość . Ściany boczne są trójkątami ostrokątnymi. Miara kąta między sąsiednimi ścianami bocznymi jest równa . Wyznaczymy objętość tego ostrosłupa.
Rozwiązanie:
Zaczynamy od rysunku:
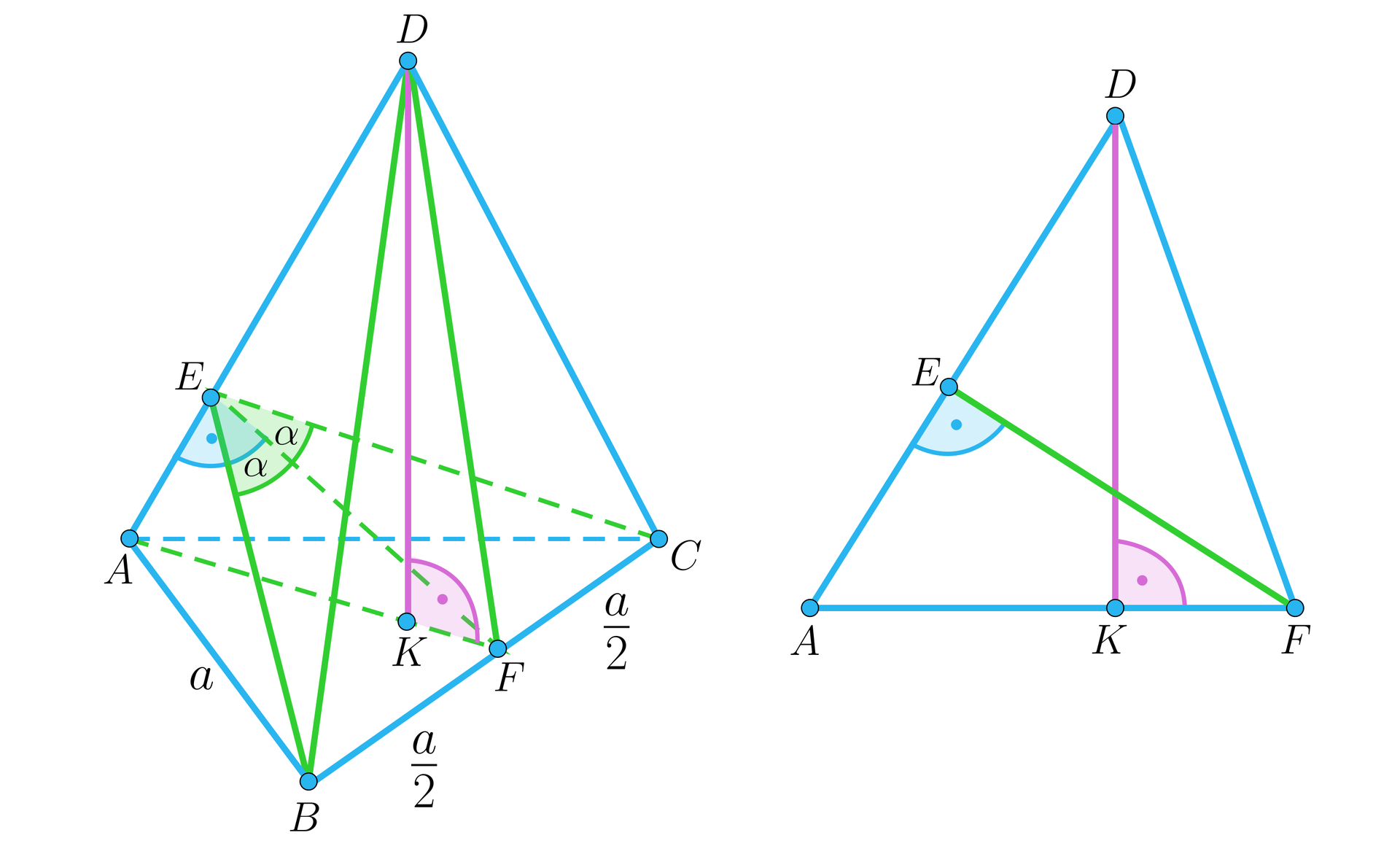
Z trójkąta mamy: , stąd .
Odcinek wyznaczamy jako wysokości podstawy.
Wiemy z określenia kąta dwuściennego, że płaszczyzna w której zawiera się trójkąt jest prostopadła do krawędzi bocznej , odcinek jest prostopadły do krawędzi bocznej .
Na podstawie twierdzenia Pitagorasa dla trójkąta mamy:
.
Zauważmy, że trójkąty i są podobne (oba są prostokątne i mają wspólny kąt ). Korzystamy z proporcji:
, stąd
.
Obliczamy objętość:
.
Słownik
rzut prostokątny wierzchołka bryły na płaszczyznę podstawy
ostrosłup prawidłowy trójkątny, którego wszystkie cztery ściany są trójkątami równobocznymi