Przeczytaj

Liczby Fibonacciego tworzone są w ten sposób, że każda następna liczba (począwszy od czwartej liczby ciągu, czyli liczby o numerze $3$ ) jest sumą dwóch liczb bezpośrednio ją poprzedzających. Przy czym najmniejsza liczba to $0$ , a dwie następne to $1$ i $1$ .

Zatem liczby o numerach $0$ , $1$ , $2$ to odpowiednio $0$ , $1$ , $1$

Liczba o numerze $3$ to $1 + 1$ , czyli $2$ .

Liczba o numerze $4$ to $1 + 2$ , czyli $3$ .

Liczba o numerze $5$ to $2 + 3$ , czyli $5$ .

Itd.

Ciąg Fibonacciego $(F_{n})$ , to ciąg (określony w zbiorze wszystkich liczb naturalnych), którego wyrazami są kolejne liczby Fibonacciego:

R7mSlo2TvNpZx

Grafika przedstawia zestawienie liczb naturalnych z kolejnymi elementami ciągu Fibonacciego. Tabela zbudowana jest z 2 wierszy. W górnym wierszu znajdują się liczby naturalne n. W dolnym wierszu umieszczone są kolejne wartości ciągu Fibonacciego. Liczby naturalne przyporządkowano wartościom ciągu Fibonacciego. Przyporządkowanie jest następujące: 0 z 0, 1 z 1, 2 z 1, 3 z 2, 4 z 3, 5 z 5, 6 z 8, 7 z 13, 8 z 21, 9 z 34, 10 z 55, 11 z 89, 12 z 144, 13 z 233 oraz 14 z 377. Zestawienie zakończone jest trzykropkiem, gdyż liczby naturalne oraz ciąg Fibonacciego ciągną się w nieskończoność. Pod tabelą pokazane zostało równanie: 5 plus 8 równa się 13. Równanie pokazuje sposób tworzenia kolejnych elementów ciągu Fibonacciego.

Liczby Fibonacciego odegrały znaczącą rolę w rozwoju teorii liczb, a także w rozwoju innych dziedzin wiedzy matematycznej. Doceniając ich znaczenie, dzień $23$ listopada ustanowiono Dniem Fibonacciego ( $1$ , $1$ i $2$ , $3$ to kolejne liczby Fibonacciego).

Przykład 1

Znajdziemy wyraz $F_{15}$ ciągu Fibonacciego.

Skorzystamy z przedstawionej powyżej tabelki, z której odczytamy wyrazy $F_{13}$ i $F_{14}$ .

$F_{15} = F_{13} + F_{14}$

$F_{15} = 233 + 377 = 610$

Ciąg Fibonacciego $(F_{n})$ najłatwiej jest zdefiniować rekurencyjnie:

F_{n} = \{\begin{cases} 0, & n = 0 \\ 1, & n = 1 \\ F_{n - 1} + F_{n - 2}, & n > 1 \end{cases}

Ciąg ten można też definiować pomijając wyraz równy $0$ , wtedy wzór rekurencyjny ciągu jest następujący:

F_{n} = \{\begin{cases} 1, & n = 1 \\ 1, & n = 2 \\ F_{n - 1} + F_{n - 2}, & n > 2 \end{cases}

RxyXkFmtBvflz

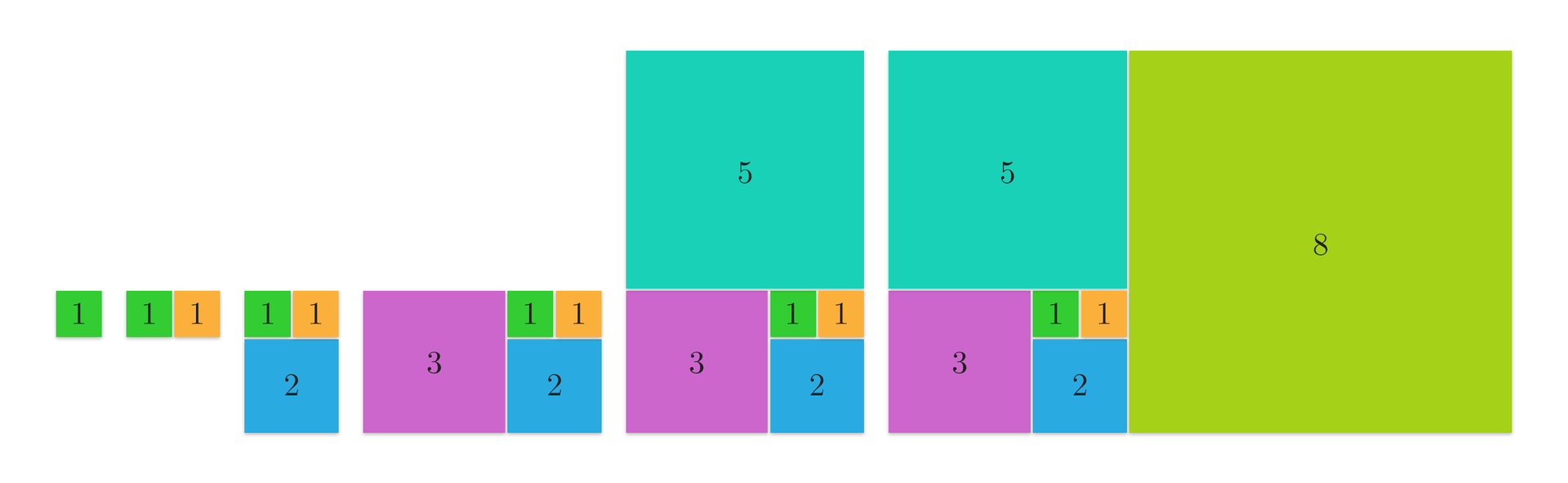
Grafika przedstawia powstawanie ciągu kwadratów, których długości boków są kolejnymi liczbami ciągu Fibonacciego. Przedstawione zostało 6 kroków, w których dodawane są kolejne kwadraty aż do uzyskania kwadratu o długości boku 8. Krok 1: mały kwadrat z cyfrą 1, o długości boku 1. Krok 2: 2 kwadraty tej samej wielkości oznaczone cyfrą 1 złączone ze sobą bokami. Krok 3: 2 kwadraty tej samej wielkości z cyfrą 1 złączone ze sobą bokami, oraz przylegający od spodu kwadrat o długości boku równej dwóm mniejszym kwadratom. Krok 4: Do istniejących już kwadratów z lewej strony dodany został kwadrat o boku równym jednemu kwadratowi z liczbą 1 i kwadratowi z liczbą 2, zatem długość boku tego kwadratu jest równa 3. Krok 5: Do narysowanych już kwadratów dodany został kwadrat z liczbą 5, który od góry przylega do dwóch kwadratów z wartością jeden oraz kwadratu z wartością 3, zatem długość jego boku to 5. Krok 6: Z prawej strony istniejących kwadratów pojawia się kwadrat z liczbą 8. Przylega on do kwadratu z cyfrą 5, jednego kwadratu z cyfrą 1 i kwadratu z cyfrą 2, długość boku tego kwadratu to 8. — Ciąg kwadratów, których długości boków są kolejnymi liczbami ciągu Fibonacciego

Wyrazy ciągu Fibonacciego mają wiele ciekawych własności. Niektóre z nich przedstawiono w poniższych przykładach.

Przykład 2

Wyrazy ciągu Fibonacciego – własności
$0$	$1$	$1$	$2$	$3$	$5$	$8$	$13$	$21$	$34$	$55$	$89$	$144$	$233$

Zaobserwujmy podzielność wyrazów ciągu Fibonacciego.
Co trzeci wyraz ciągu Fibonacciego jest podzielny przez $2$ , począwszy od wyrazu $F_{3} = 2$ .

Co czwarty wyraz ciągu Fibonacciego jest podzielny przez $3$ , począwszy od wyrazu $F_{4} = 3$ .

Co piąty wyraz ciągu Fibonacciego jest podzielny przez $5$ , począwszy od wyrazu $F_{5} = 5$ .

Przykład 3

Określimy jeszcze kilka własności wyrazów ciagu Fibonaccciego. Suma dowolnych dziesięciu kolejnych wyrazów ciągu Fibonacciego (pierwszą dziesiątkę liczb rozpoczynamy od wyrazu $F_{1}$ ) jest podzielna przez $11$ .

Wyraz ciągu Fibonacciego równy kwadratowi swojego indeksu to $F_{12} = 12^{2} = 144$ .

Największy znany wyraz ciągu Fibonacciego składający się z cyfr nieparzystych to $F_{22} = 17711$ .

Niektóre liczby Fibonacciego to liczby pierwsze np. $2$ , $3$ , $5$ , $13$ , $89$ , $233$ , $. . .$
Prawdopodobnie tych liczb w ciągu jest nieskończenie wiele.

Każdą liczbę naturalną można przedstawić jako sumę liczb Fibonacciego.
Np.
$1000000 = 832040 + 121393 + 46368 + 144 + 55$
$1000000 = F_{30} + F_{26} + F_{24} + F_{12} + F_{10}$ .

Przykład 4

Ciąg Fibonacciego można opisać wzorem ogólnym $F_{n} = \frac{{(1 + \sqrt{5})}^{n} - {(1 - \sqrt{5})}^{n}}{2^{n} \cdot \sqrt{5}}$ .

Obliczymy na podstawie tego wzoru $F_{3}$ .

$F_{3} = \frac{{(1 + \sqrt{5})}^{3} - {(1 - \sqrt{5})}^{3}}{2^{3} \cdot \sqrt{5}}$

$F_{3} = \frac{(1 + 3 \sqrt{5} + 3 \sqrt{25} + 5 \sqrt{5}) - (1 - 3 \sqrt{5} + 3 \sqrt{25} - 5 \sqrt{5})}{8 \cdot \sqrt{5}}$

$F_{3} = \frac{16 \sqrt{5}}{8 \sqrt{5}} = 2$

Pokażemy teraz zastosowanie liczb Fibonacciego w obliczeniach kombinatorycznych.

Przykład 5

Mamy do dyspozycji płyty o wymiarach $2 \times 1$ . Chcemy nimi wyłożyć plac o wymiarach $2 \times n$ , gdzie $n \in ℕ$ . Niech $a_{n}$ będzie liczbą różnych pokryć tego placu płytami.

Na rysunku pokazane są sposoby ułożenia płyt na placu o wymiarach odpowiednio $2 \times 1$ , $2 \times 2$ , $2 \times 3$ .

R1BjIpTYwGQw2

Rysunek przedstawia sposób ułożenia płyt na polach o wymiarach podanych w zadaniu. Najpierw pokazany jest prostokąt o stosunku boków 2 do 1, gdzie krótszy bok ustawiony jest poziomo, a dłuższy pionowo. Jest pod nim podpis: a, dolny indeks, 1, równa się 1. Następnie przedstawione zostały 2 sposoby ułożenia dwóch prostokątów o stosunku boków 2 do 1. Pierwszy sposób: 2 prostokąty przylegające do siebie dłuższymi bokami, gdzie dłuższy bok ma orientację pionową. Drugi sposób: 2 prostokąty połączone dłuższymi bokami, gdzie dłuższy bok ma orientację poziomą. Pod rysunkami znajduje się napis: a, dolny indeks, 2, równa się 2. Na końcu pokazane zostały 3 sposoby ułożenia trzech prostokątów. Sposób pierwszy: 3 prostokąty, przylegające do siebie dłuższymi bokami, gdzie dłuższy bok ma orientację pionową. Drugi sposób: 1 prostokąt, jest ustawiony tak, że jego dłuższy bok ma orientację pionową. Do jego dłuższego boku z prawej strony przylegają krótszymi bokami dwa połączone ze sobą dłuższym bokiem prostokąty. Dłuższe boki dwóch prostokątów mają orientację poziomą. Ostatni sposób jest odbiciem lustrzanym sposobu drugiego. Pod ostatnimi trzema sposobami jest podpis: a, dolny indeks, 3, równa się 3.

Przyjmujemy też, że $a_{0} = 1$ .

Wykażemy, że dla każdej liczby naturalnej $n \geq 3$ prawdziwa jest równość

$a_{n} = a_{n - 2} + a_{n - 1}$

Dowód:

Jeśli należy pokryć plac płytami o wymiarach $2 \times n$ , to płytę możemy położyć pionowo lub poziomo.

RpzdIUl2x6TlU

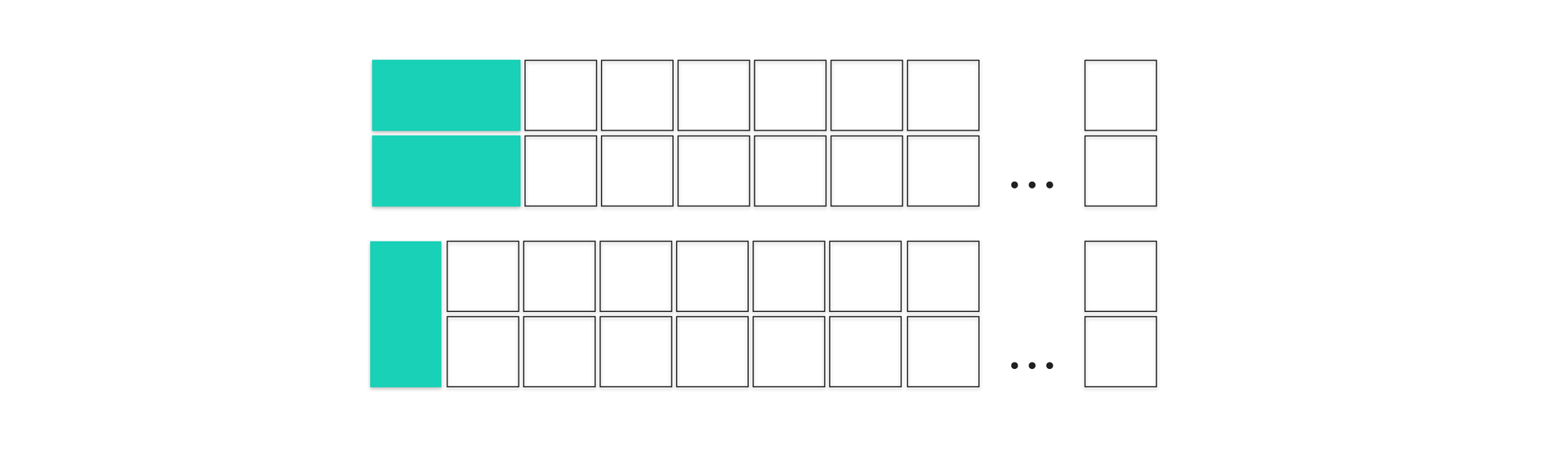
Grafika przedstawia dwa szeregi kwadratów. Oba szeregi składają się z dwóch wierszy, a w każdym wierszu znajduje się dziewięć kwadratów, przy czym ostatnia para kwadratów oddzielona jest od reszty trzykropkiem, co oznacza że w rzeczywistości szereg składa się z większej ilości elementów niż zostało pokazane na rysunku. W pierwszym szeregu dwa pierwsze kwadraty w każdym wierszu zostały połączone i zamalowane na zielono. Dzięki czemu powstały dwa prostokąty o wysokości jednego kwadratu i długości dwóch kwadratów. Połączone ze sobą dłuższym bokiem, których krótszy bok ma orientację poziomą. W drugim szeregu zamalowane zostały po jednym kwadracie w każdym wierszu. Dzięki czemu powstał jeden prostokąt o szerokości jednego kwadratu i wysokości dwóch kwadratów. Jego dłuższy bok ma orientację pionową.

Jeżeli płyta na pierwszym polu leży poziomo to należy pokryć pozostałą część placu o wymiarach $2 \times (n - 2)$ . Jest $a_{n - 2}$ możliwości tego dokonania.

Jeżeli płyta leży pionowo, to należy pokryć pozostałą część placu o wymiarach $2 \times (n - 1)$ . Jest $a_{n - 1}$ możliwości tego dokonania.

Dodając te liczby, otrzymujemy

$a_{n} = a_{n - 2} + a_{n - 1}$

Zauważmy, że dla każdej liczby naturalnej $n$

$a_{n} = F_{n + 1}$

Rzeczywiście,

$a_{1} = 1 = F_{2}$

$a_{2} = 2 = F_{3}$

oraz ta sama zasada rekurencjizasada rekurencji obowiązuje dla ciągu $(a_{n})$ i $(F_{n})$ zatem $a_{n} = F_{n + 1}$ .

Przykład 6

Przyjrzyjmy się zależności między trzema kolejnymi wyrazami ciągu Fibonacciego.

RQyHFGqsZ6t7e

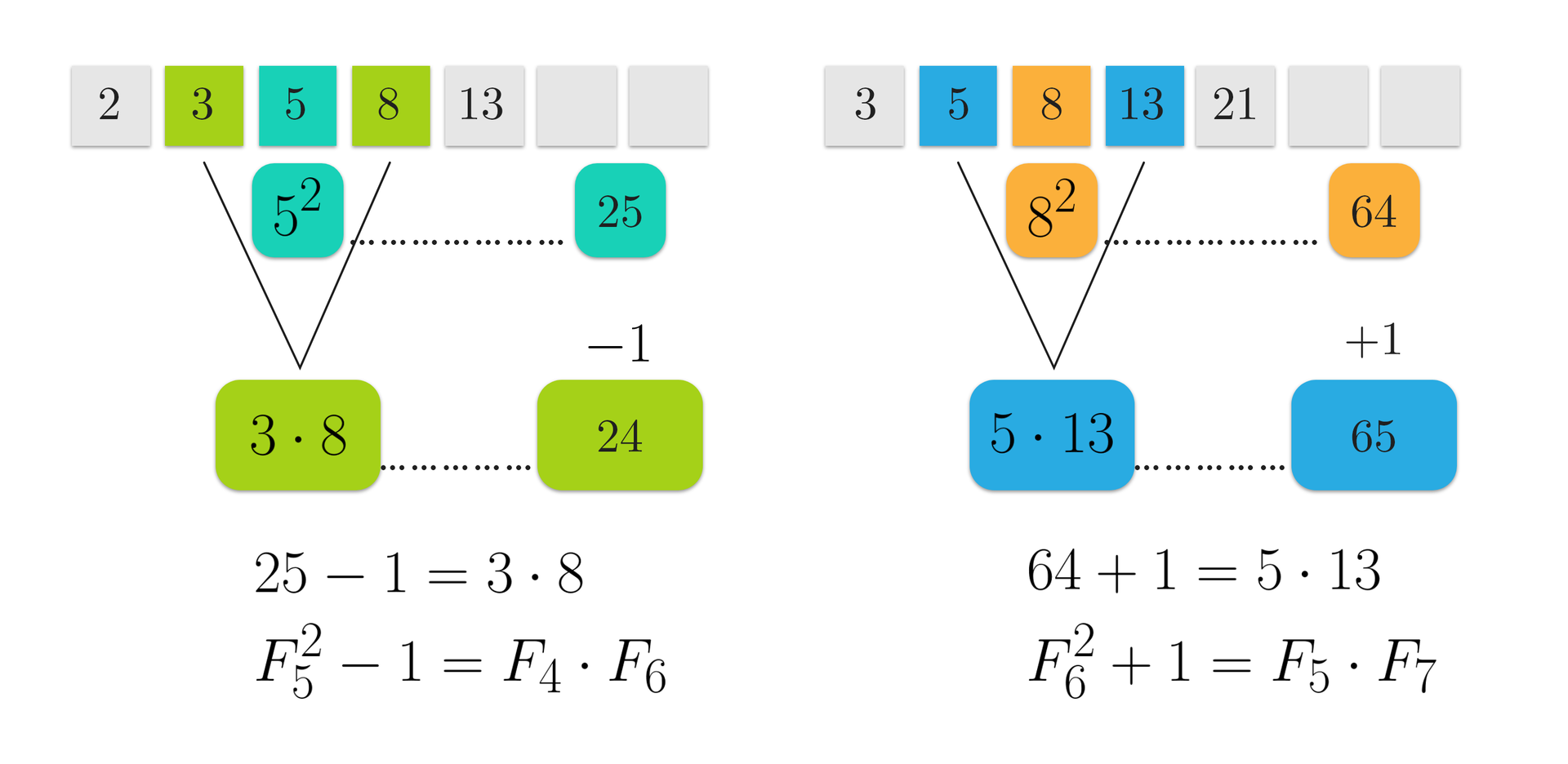
Grafika przedstawia dwa grafy. Pierwszy z nich rozpoczyna się od 7 kwadratów, gdzie pierwsze 5 jest oznaczone liczbami kolejno: 2, 3, 5, 8, 13, a dwa ostatnie są puste. Bezpośrednio pod kwadratem z cyfrą5 pięć znajduje się kwadrat z napisem: 5 do potęgi 2. Jest on połączony ze znajdującym się po prawej stronie kwadratem z liczbą 25. Poniżej kwadratu z napisem: 5 do potęgi 2 znajduje się prostokąt z lewą stroną równania trzy razy 8. Cyfry 3 i 8 znajdujące się w kwadratach są połączone z częścią równania za pomocą linii. Lewa strona równania jest również połączona z znajdującym się po prawej stronie wynikiem liczbą 24. Nad kwadratem z liczbą 24 zapisana została liczba minus 1. Pod pierwszym grafem zapisane są równania: 25, minus 1, równa się, 3, razy,8. F, dolny indeks, 5, minus 1, równa się, F, dolny indeks, 4, razy, F, dolny indeks,6. Drugi graf również rozpoczyna się od siedmiu kwadratów, gdzie pierwsze pięć jest oznaczone liczbami kolejno: 3, 5, 8, 13, 21, a dwa ostatnie kwadraty są puste. Bezpośrednio pod kwadratem z cyfrą 8 znajduje się kwadrat z napisem: 8 do potęgi 2, który jest połączony z znajdującą się po prawej stronie liczbą 64. Poniżej napisu, znajduje się lewa część równania: 5, razy, 13, a jego wynik pokazany jest po prawej stronie jest równy 65. Nad liczbą 65 jest zapisana liczba plus 1. Pod drugim grafem zapisane zostały równania: 64, dodać,1, równa się,5, razy,13. Oraz F, dolny indeks, 6, dodać, 1, równa się, F, dolny indeks, 5, razy, F, dolny indeks, 7.

Wniosek:

Jeśli dane są trzy kolejne wyrazy ciągu Fibonacciego to kwadrat wyrazu środkowego, odpowiednio zwiększony bądź zmniejszony o $1$ jest równy iloczynowi wyrazów sąsiednich.

$F_{n}^{2} - {(- 1)}^{n - 1} = F_{n - 1} \cdot F_{n + 1}$

Ciąg Fibonacciego można określić też dla indeksów ujemnych.

$F_{n - 2} = F_{n} - F_{n - 1}$

Czyli

$F_{(- n)} = {(- 1)}^{n + 1} \cdot F_{n}$

Ciąg Fibonacciego dla indeksów ujemnych i dodatnich
$n$	$. . .$	$- 6$	$- 5$	$- 4$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$. . .$
$F_{n}$	$. . .$	$- 8$	$5$	$- 3$	$2$	$- 1$	$1$	$0$	$1$	$1$	$2$	$3$	$5$	$8$	$. . .$

Przykład 7

Obliczymy wyraz $F_{(- 8)}$ ciągu Fibonacciego.

Skorzystamy ze wzoru

$F_{(- n)} = {(- 1)}^{n + 1} \cdot F_{n}$

$F_{(- 8)} = {(- 1)}^{8 + 1} \cdot F_{8}$

$F_{(- 8)} = (- 1) \cdot 21 = - 21$ .

Słownik

ciąg Fibonacciego

(F_{n})

zdefiniowany rekurencyjnie

ciąg Fibonacciego

(F_{n})

zdefiniowany rekurencyjnie

F_{n} = \{\begin{cases} 0, & n = 0 \\ 1, & n = 1 \\ F_{n - 1} + F_{n - 2}, & n > 1 \end{cases}

Wprowadzenie

Film edukacyjny

Słownik