Przeczytaj
Nierównością wymierną nazywamy nierówność postaci: lub , lub , lub , gdzie i są wielomianami i nie jest wielomianem zerowym.
Dwie nierówności wymierne określone w tej samej dziedzinie nazywamy równoważnymi, jeżeli mają te same zbiory rozwiązań.
Jeżeli zbiór zawiera się w zbiorze , to dopełnieniem zbioru do zbioru nazywamy zbiór i oznaczamy go symbolem .
Zbiór jest zbiorem rozwiązań nierówności: , a zbiór zbiorem rozwiązań nierówności: . Wyznacz zbiory: , , , , , , oraz .
Rozwiązanie:
W celu wyznaczenia poszukiwanych zbiorów kolejno rozwiążemy nierówności:
• określamy dziedzinę nierówności: | |
• odejmujemy liczbę od obu stron nierówności: | • dodajemy liczbę do obu stron nierówności: |
• sprowadzamy wyrażenia do wspólnego mianownika: | |
• doprowadzamy ułamek do postaci nieskracalnej: | |
• zamieniamy otrzymany ułamek na postać iloczynową, co wynika z identyczności znaku ilorazu i znaku iloczynuidentyczności znaku ilorazu i znaku iloczynu: | |
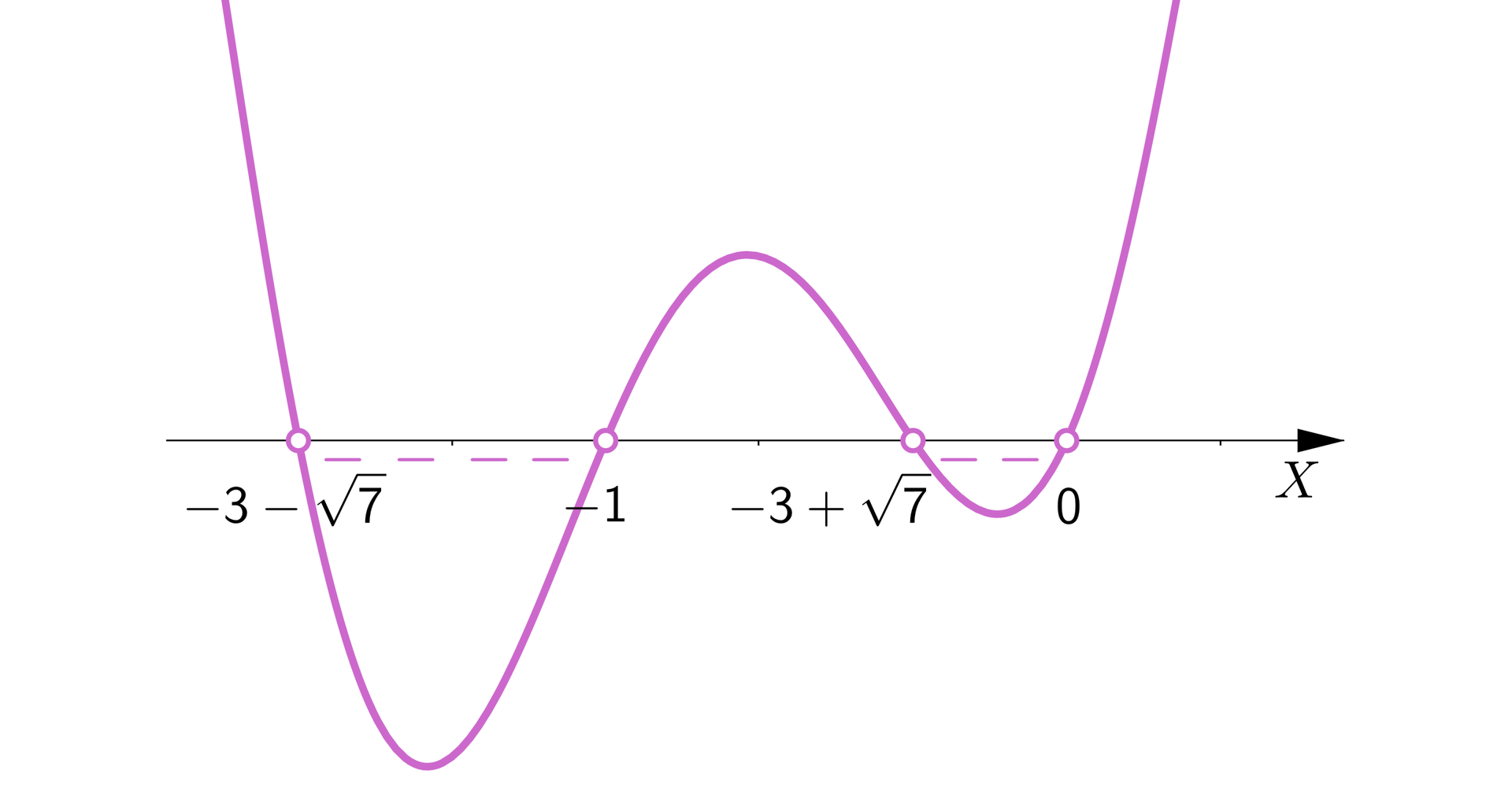
• sporządzamy ilustrację graficzną nierówności i odczytujemy jej rozwiązania z uwzględnieniem ustalonej dziedziny: | |
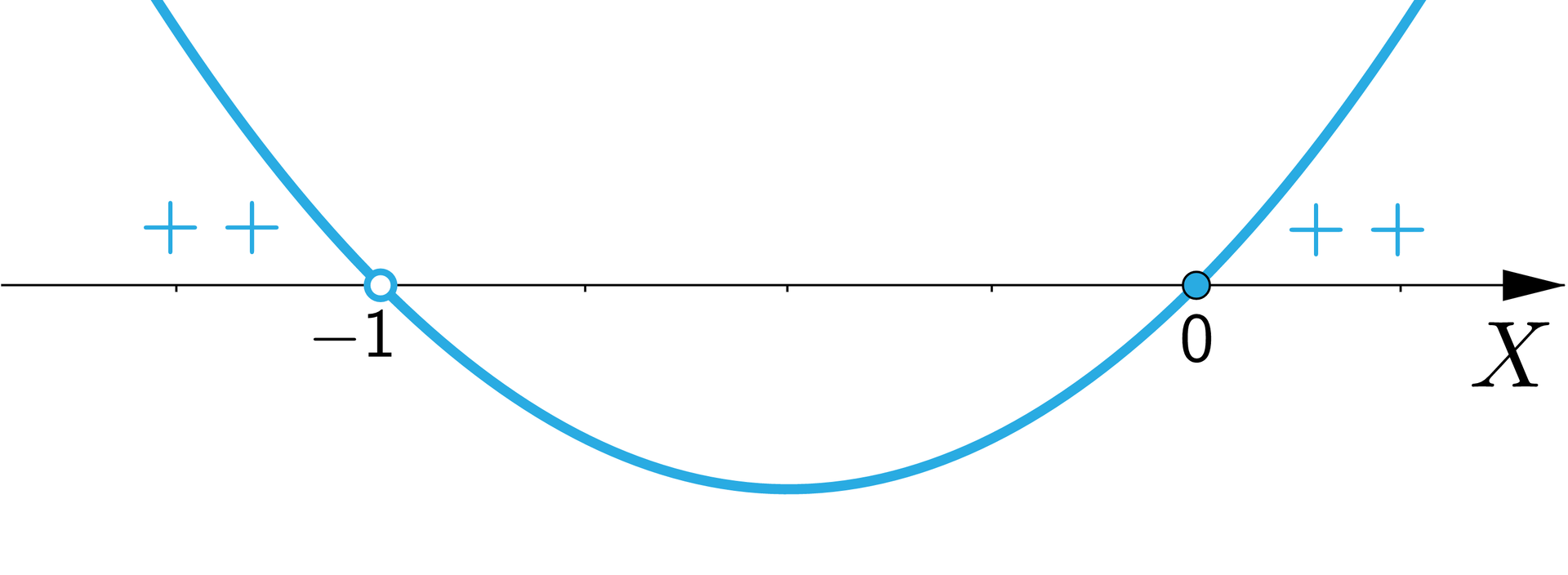 | 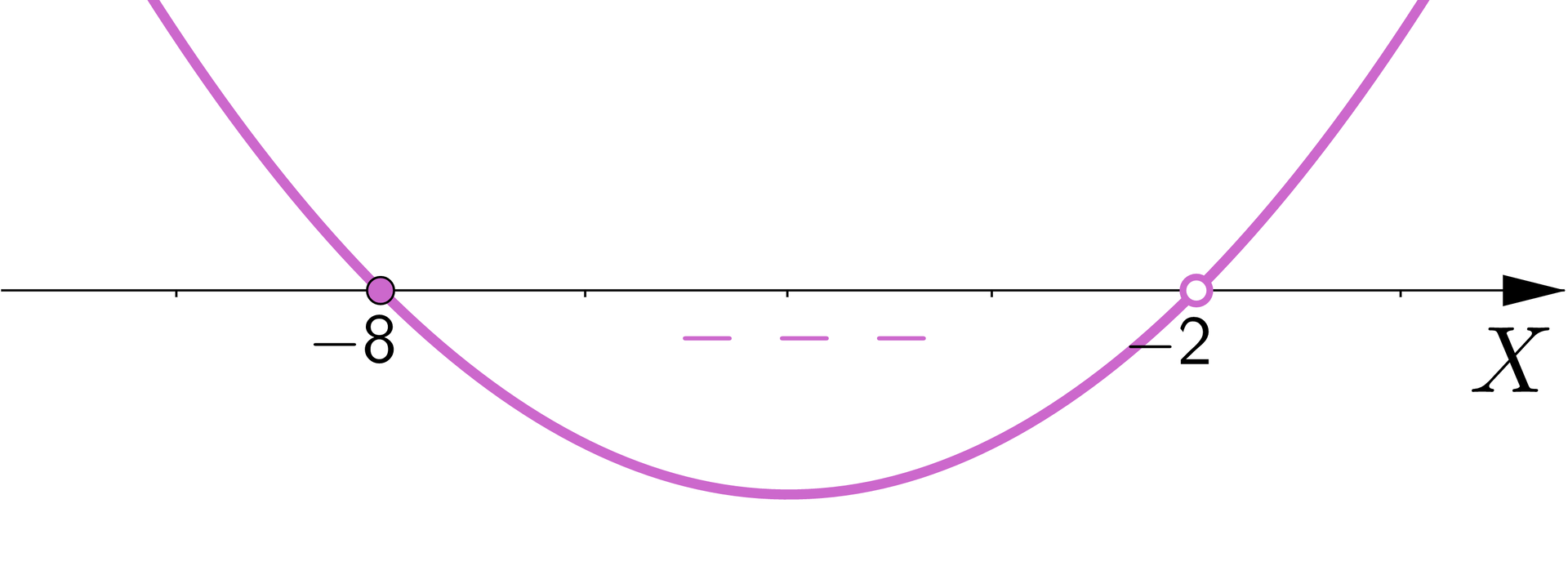 |
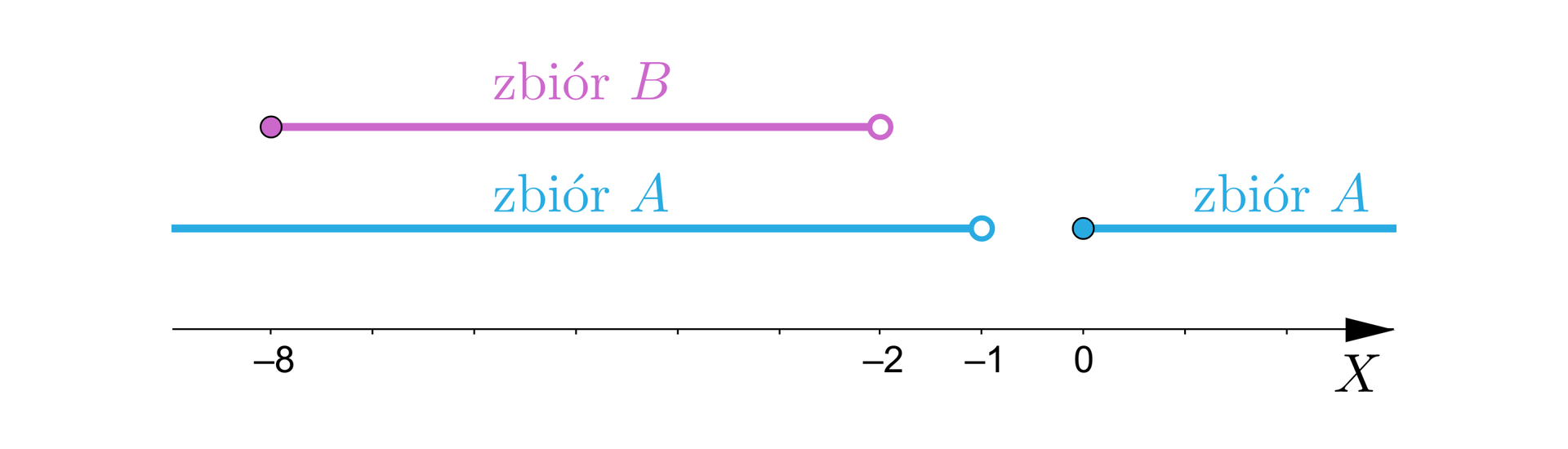 | |
, ponieważ zbiór jest podzbiorem | |
, ponieważ zbiór jest podzbiorem | |
W celu wyznaczenia poszukiwanych zbiorów kolejno rozwiążemy nierówności:
Zacznamy od określenia dziedziny nierówności , czyli .
Odejmujemy liczbę od obu stron nierówności:
.
Sprowadzamy wyrażenie do wspólnego mianownika
,
a następnie doprowadzamy ułamek do postaci nieskracalnej
,
.
Zamieniamy otrzymany ułamek na postać iloczynową, co wynika z identyczności znaku ilorazu i znaku iloczynuidentyczności znaku ilorazu i znaku iloczynuą
.
Sporządzamy ilustrację graficzną nierówności i odczytujemy jej rozwiązania z uwzględnieniem ustalonej dziedziny.
Na rysunku przedstawiona jest pozioma oś X oraz wykres funkcji w kształcie paraboli z ramionami skierowanymi do góry przecinający podaną oś w punkcie , który nie należy do rozwiązania oraz w punkcie , który należy do rozwiązania. Na lewo od argumentu wykres znajduje się nad osią X i oznaczono ten fragment plusami oraz na prawo od argumentu wykres również znajduje się na osią X i oznaczono ten obszar plusami.
.
Przejdziemy do wzynaczenia zbioru .
Ponownie zaczniemy od wyznaczenia dziedziny nierówności , czyli .
Dodajemy liczbę 3 do obu stron nierówności:
.
Sprowadzamy wyrażenie do wspólnego mianownika
,
a następnie doprowadzamy ułamek do postaci nieskracalnej
.
Zamieniamy otrzymany ułamek na postać iloczynową, co wynika z identyczności znaku ilorazu i znaku iloczynuidentyczności znaku ilorazu i znaku iloczynu.
Sporządzamy ilustrację graficzną nierówności i odczytujemy jej rozwiązania z uwzględnieniem ustalonej dziedziny:
Na rysunku przedstawiona jest pozioma oś X oraz wykres funkcji w kształcie paraboli z ramionami skierowanymi do góry przecinający podaną oś w punkcie , który należy do rozwiązania oraz w punkcie , który nie należy do rozwiązania. Część wykresu znajduje się pod osią X między argumentem a i oznaczono ten obszar trzema minusami.
.
Stworzymy ilustrację graficzną przedstawiającą obydwa zbioru na wspólnej osi :
Na rysunku przedstawiona jest pozioma oś X od minus ośmiu do dwóch. Nad osią zaznaczone są zbiory A oraz B. Zbiór A składa się z dwóch półprostych. Pierwsza półprosta leży nad osią X od minus nieskończoności do punktu , który nie należy do zbioru A . Druga prosta również leżąca nad osią X zaczyna się w punkcie , który należy do zbioru A i kończy w plus nieskończoności. Odcinek oznaczający zbiór B leży nad argumentem , który należy do zbiory B i kończy się nad argumentem nie należącym do zbioru B.
Zatem
oraz .
Następnie
, ponieważ zbiór jest podzbiorem ,
, ponieważ zbiór jest podzbiorem ,
,
.
Dla jakich liczb i spełniona jest nierówność: ?
Rozwiązanie
Ustalamy, że liczby i muszą być różne od zera:
zał.:
Stosujemy przekształcenia równoważneprzekształcenia równoważne aż uzyskamy najprostszą postać nierówności:
W liczniku ułamka otrzymaliśmy kwadrat sumy, który jest nieujemny dla dowolnych liczb rzeczywistych. Mianownik zaś jest dodatni dla liczb i o jednakowych znakach.
Zatem nierówność jest spełniona dla liczb i o równych znakach (obie dodatnie lub obie ujemne) oraz dowolnej pary liczb przeciwnych, tzn. . W tym ostatnim przypadku badany ułamek przyjmuje wartość zero.
Dla jakich wartości parametru suma odwrotności kwadratów pierwiastków równania jest mniejsza od ?
Rozwiązanie
W pierwszym etapie rozwiązania zadania należy ustalić dla jakich wartości parametru dane równanie posiada rozwiązania (jedno lub dwa). Warunkiem jest, aby .
lub
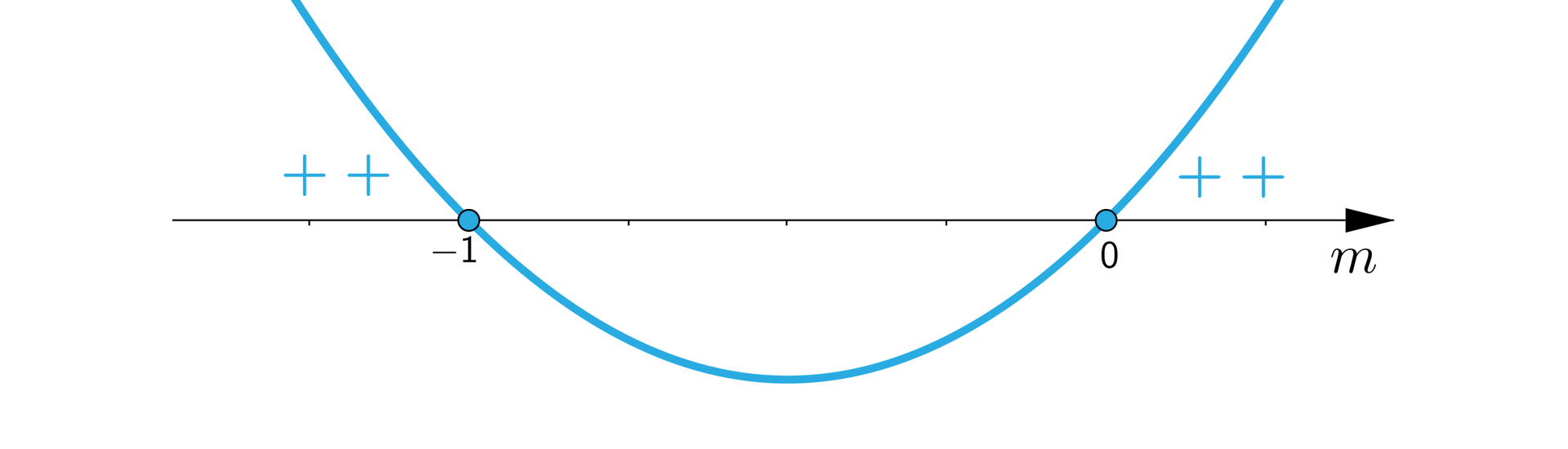
W drugim etapie rozwiązania zapisujemy warunek wynikający z treści zadania:
Korzystając ze wzorów Viete'a, otrzymujemy:
Ponieważ , , więc podstawiając powyżej otrzymujemy nierówność wymierną z niewiadomą :
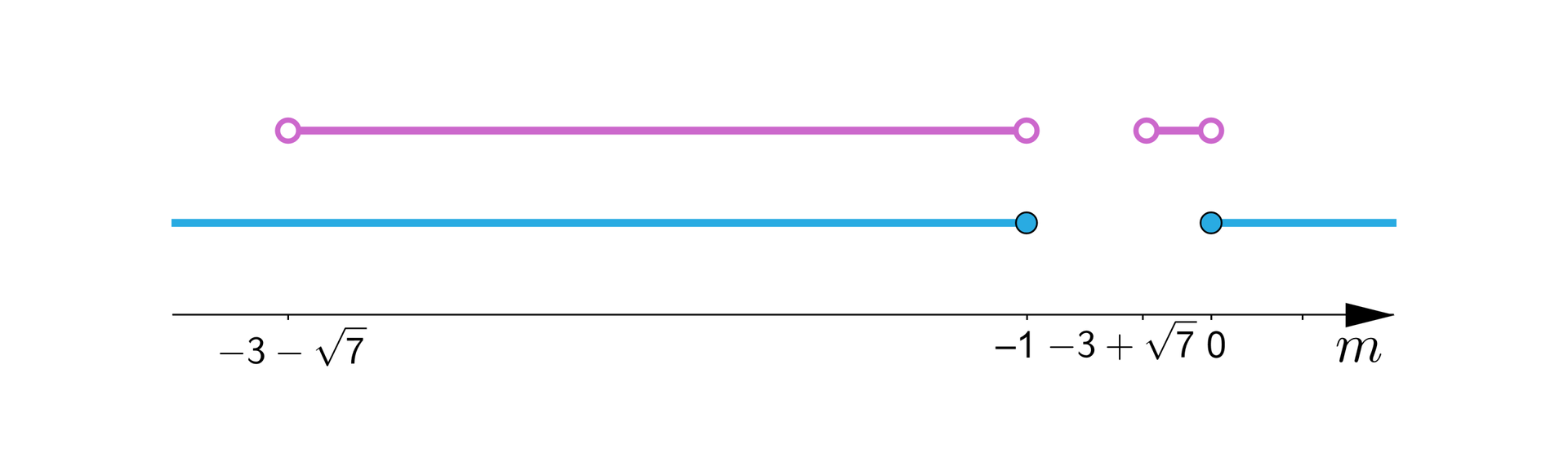
Założenia: oraz
,
Obydwa rozważane warunki muszą być spełnione jednocześnie, zatem wskazujemy iloczyn (część wspólną) rozwiązań obu nierówności:
Przedsiębiorca rozważa zastosowanie jednej z dwóch linii produkcyjnych. Uruchomienie linii kosztuje , a koszt produkcji każdej sztuki produktu wynosi . W przypadku linii wartości te wynoszą odpowiednio i .
Ile minimalnie sztuk produktu trzeba wyprodukować korzystając z , a ile korzystając z , aby średni koszt produkcji sztuki był niższy niż ?
Przy jakiej wielkości produkcji średni koszt produkcji sztuki jest niższy przy użyciu linii ?
Zakładając, że cena sprzedaży sztuki produktu wynosi oraz, że przedsiębiorca sprzeda wszystkie wyprodukowane egzemplarze, oblicz wielkość produkcji dla każdej z linii, która zagwarantuje dodatni zysk.
Rozwiązanie:
Przyjmijmy oznaczenie: – wielkość produkcji w sztukach, .
Średni koszt produkcji sztuki wynosi: | |
|---|---|
W toku rozwiązania tych nierówności wymiernych można pomnożyć obie strony nierówności przez , ponieważ pozwala na to założenie dotyczące znaku zmiennej : | |
a) Należy wyprodukować przynajmniej szt. produktu. | a) Należy wyprodukować przynajmniej szt. produktu. |
Dysponując podanymi informacjami tworzymy, a następnie rozwiązujemy nierówność wymierną: | |
b) Niższy średni koszt produkcji szt. przy użyciu linii uzyskamy przy prodykcji minimum szt. | |
Zakładając, że cena sprzedaży szt. produktu wynosi , przy sprzedaży sztuk osiągnięty zostanie przychód . Zatem zysk uzyskany przez przedsiębiorcę po sprzedaży sztuk można wyrazić wzorem: | |
Wielkość produkcji gwarantującą osiągnięcie dodatniego zysku obliczymy rozwiązując nierówności: | |
 |
 |
Minimalna wielkość produkcji gwarantująca dodatni zysk to sztuk produktu. | Minimalna wielkość produkcji gwarantująca dodatni zysk to sztuki produktu. |
Zaczniemy od wyznaczenia ile minimalnie sztuk produktu trzeba wyprodukować korzytając z aby średni koszt produkcji sztuki był niższy niż .
.
.Dysponując informacjami z podpunktu (a), tworzymy, a następnie rozwiązujemy nierówność wymierną:
Zatem niższy średni koszt produkcji szt. przy użyciu linii uzyskamy przy prodykcji minimum sztuk.
Zakładając, że cena sprzedaży szt. produktu wynosi , przy sprzedaży sztuk osiągnięty zostanie przychód . Zatem zysk uzyskany przez przedsiębiorcę po sprzedaży sztuk można wyrazić dla lini wzorem
.
Wielkość produkcji gwarantującą osiągnięcie dodatniego zysku obliczymy rozwiązując nierówności:
,
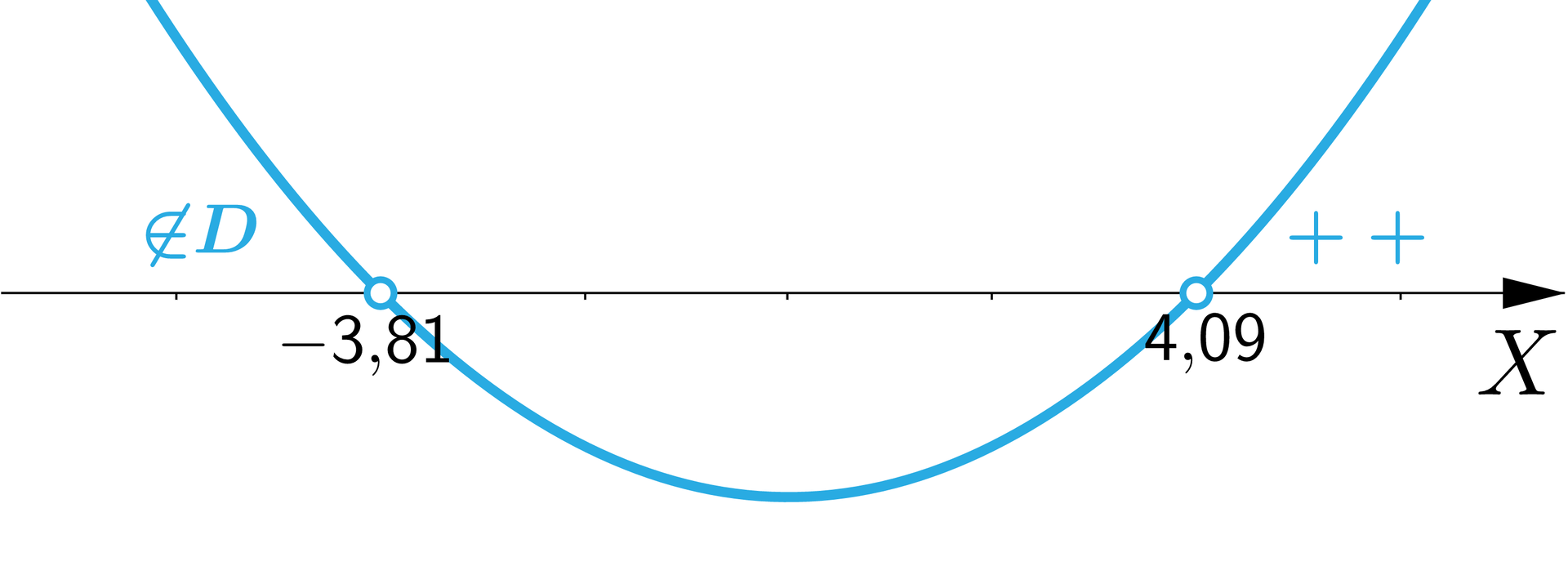
, .Sporządzamy ilustrację graficzną nierówności i odczytujemy jej rozwiązania z uwzględnieniem ustalonej dziedziny
Na rysunku przedstawiona jest pozioma oś X oraz wykres funkcji w kształcie paraboli z ramionami skierowanymi do góry przecinający podaną oś w punktach oraz , które nie należą do rozwiązania. Na lewo od argumentu wykres znajduje się nad osią X i oznaczono ten fragment oraz na prawo od argumentu wykres również znajduje się na osią X i oznaczono ten obszar plusami.
Stąd minimalna wielkość produkcji gwarantująca dodatni zysk to sztuk produktu.
Przejdziemy do wyznaczenia minimalnej wielości produkcji gwarantującej dodatni zysk dla lini . Zakładając wszystko jak dla lini zysk uzyskany przez przedsiębiorcę po sprzedaży sztuk można wyrazić wzorem
.
Wielkość produkcji gwarantującą osiągnięcie dodatniego zysku obliczymy rozwiązując nierówności:
,
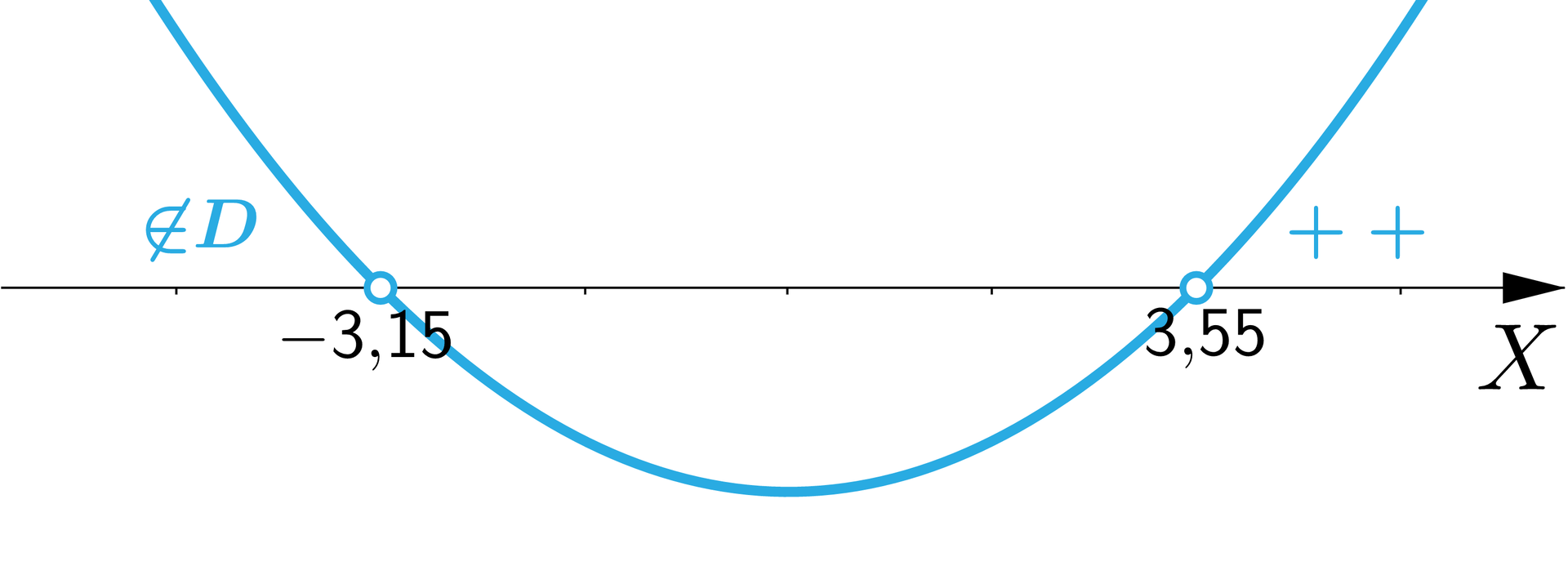
, .Sporządzamy ilustrację graficzną nierówności i odczytujemy jej rozwiązania z uwzględnieniem ustalonej dziedziny.
Na rysunku przedstawiona jest pozioma oś X oraz wykres funkcji w kształcie paraboli z ramionami skierowanymi do góry przecinający podaną oś w punktach oraz , które nie należą do rozwiązania. Na lewo od argumentu wykres znajduje się nad osią X i oznaczono ten fragment oraz na prawo od argumentu wykres również znajduje się na osią X i oznaczono ten obszar plusami.
Stąd minimalna wielkość produkcji gwarantująca dodatni zysk to sztuki produktu.
Słownik
są to przekształcenia, w wyniku których otrzymujemy nierówności równoważne. Należą do nich: dodawanie/odejmowanie liczb lub wyrażeń do obu stron nierówności; mnożenie obu stron nierówności przez liczbę dodatnią lub wyrażenie stale dodatnie; mnożenie stron nierówności przez liczbę ujemną lub wyrażenie stale ujemne – w tym ostatnim przypadku otrzymujemy nierówność o zwrocie przeciwnym w stosunku do nierówności, którą przekształcamy
w przypadku nierówności wymiernych prawdziwe są także następujące przekształcenia równoważne dla wszystkich liczb rzeczywistych , dla których :