Przeczytaj
Przekrój bryły jest figurą płaską, będącą częścią wspólną płaszczyzny przekroju oraz danej bryły.
Różne rodzaje przekrojów walca
Przekrój osiowy walca
Przekrojem osiowym walcawalca nazywamy przekrój płaszczyzną zawierającą oś obrotu walca. Tym przekrojem jest prostokąt o bokach równych średnicy podstawy oraz wysokości walca.

Przekrój poprzeczny walca
Przekrojem poprzecznym walca nazywamy przekrój płaszczyzną prostopadłą do osi obrotu walca. Tym przekrojem jest koło o promieniu równym promieniowi podstawy walca.
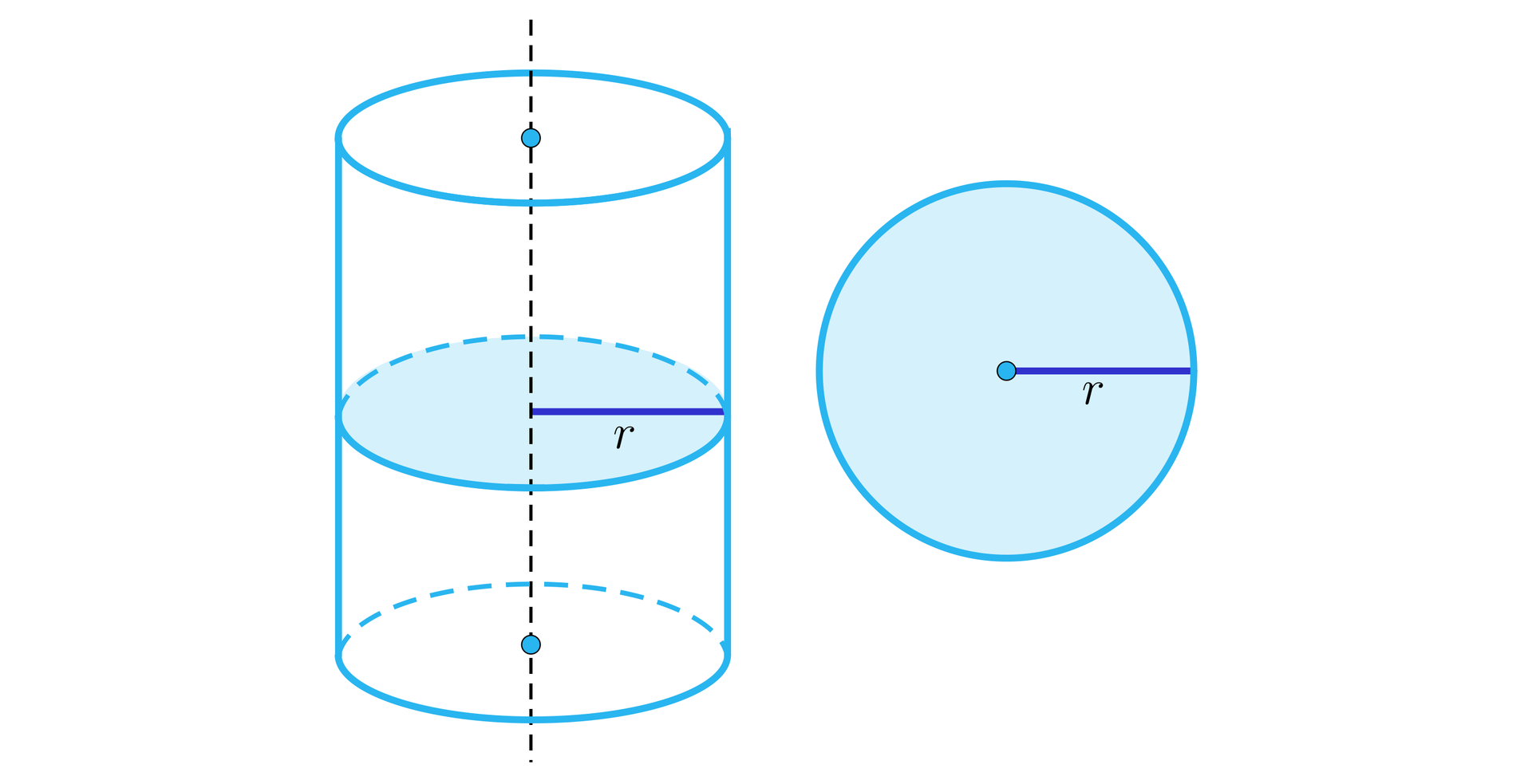
Poza przekrojem osiowym i poprzecznym walca występują również inne przekroje. Kształt tych przekrojów zależy od kąta nachylenia płaszczyzny przekroju do podstawy.
Przekrój walca płaszczyzną równoległą do osi obrotu

Przekrój walca będący elipsą

Pole elipsyelipsy przedstawionej na rysunku wyraża się wzorem
gdzie:
długość nazywamy wielką osią, a długość małą osią elipsy.

Jeżeli jest długością promienia podstawy walca, a jego wysokością, to:
Przekątna przekroju osiowego walca jest nachylona do płaszczyzny podstawy walca pod kątem . Obliczymy pole tego przekroju, jeżeli objętość walca wynosi .
Rozwiązanie
Narysujmy walec i jego przekrój osiowy wraz z odpowiednim kątem, jak na rysunku.
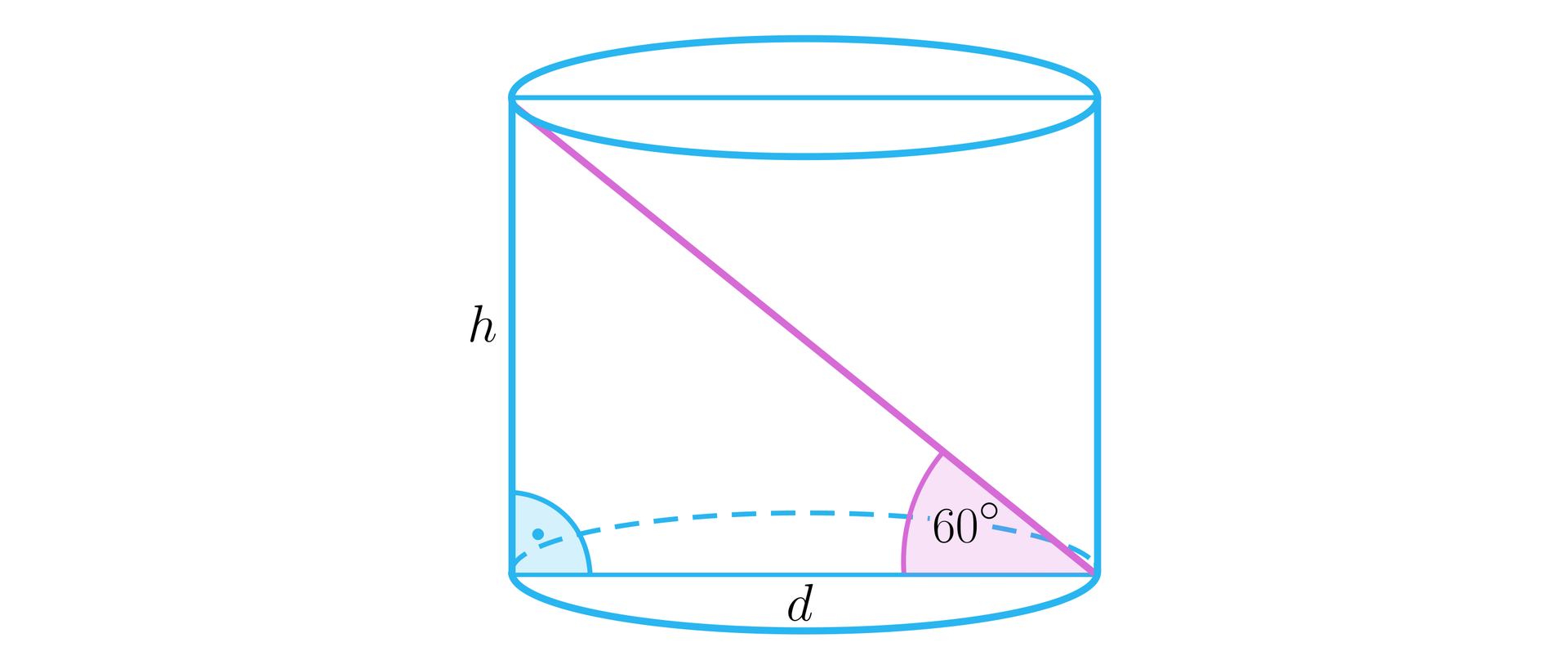
Ponieważ kąt nachylenia przekątnej przekroju osiowego walca ma miarę , zatem .
Do wyznaczenia wartości wykorzystamy wzór na objętość walca .
Wobec tego
, czyli .
Przekrój osiowy walca z rysunku jest prostokątem o bokach odpowiednio oraz . Zatem pole tego prostokąta wynosi:
.
Przekrój poprzeczny walca jest kołem o polu . Obliczymy pole powierzchni całkowitej tego walca, jeżeli wysokość walca jest razy dłuższa niż promień podstawy walca.
Rozwiązanie
Narysujmy walec, jego przekrój poprzeczny i wprowadźmy oznaczenia, jak na rysunku.
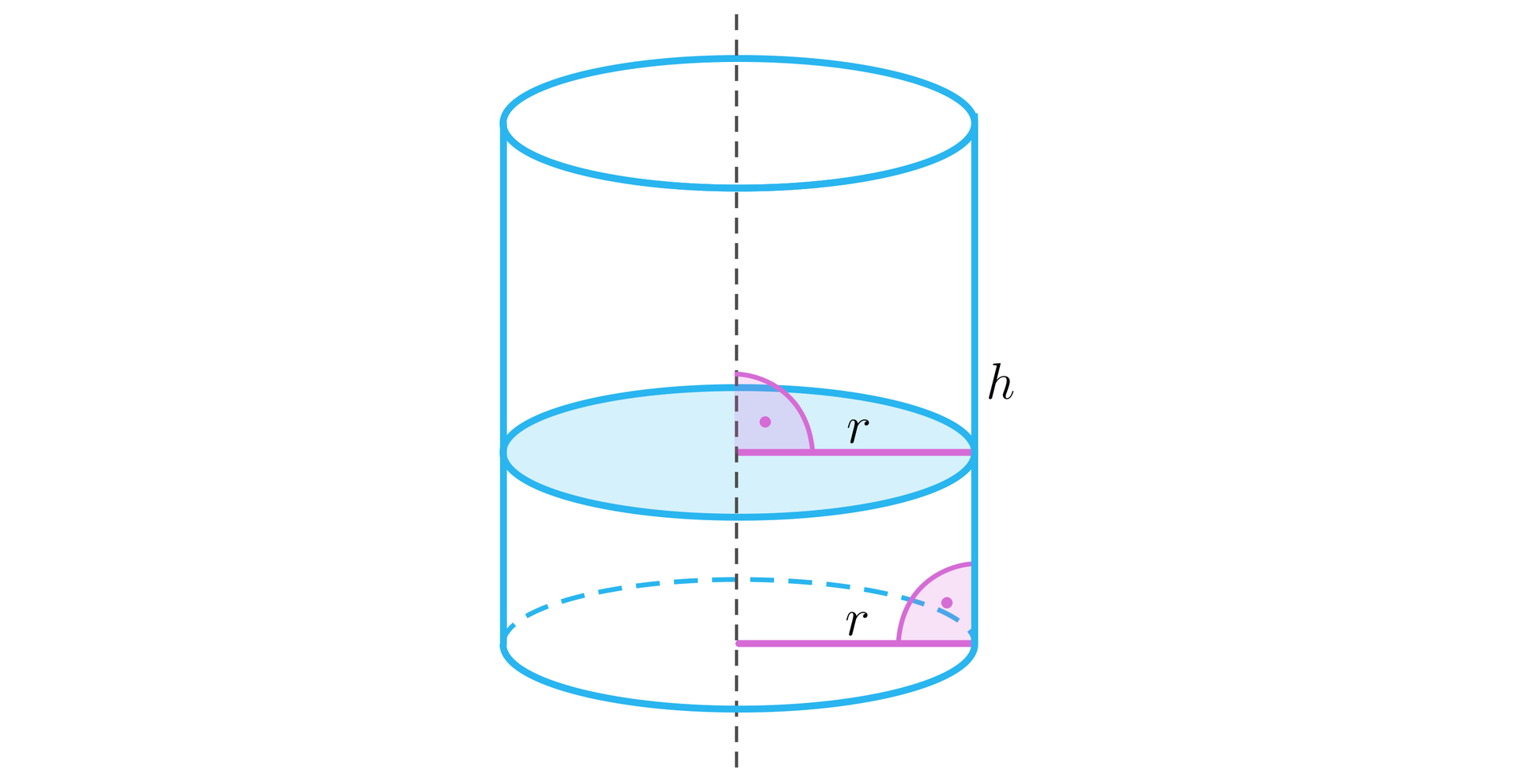
Pole przekroju poprzecznego walca jest równe polu podstawy walca. Jeżeli jest długością promienia podstawy walca, zatem do wyznaczenia wartości rozwiązujemy równanie:
, czyli .
Jeżeli jest długością wysokości walca, to .
Wobec tego pole powierzchni całkowitej walca wynosi:
.
Przekrój walca płaszczyzną równoległą do osi symetrii jest kwadratem o przekątnej długości , oddalonym od osi symetrii walca o . Obliczymy pole powierzchni całkowitej tego walca.
Rozwiązanie
Z warunków zadania wynika, że przekrój jest równoległy do osi obrotu walca.
Wobec tego narysujmy walec, jego przekrój płaszczyzną równoległą do osi obrotu oraz wprowadźmy oznaczenia, jak na rysunku.
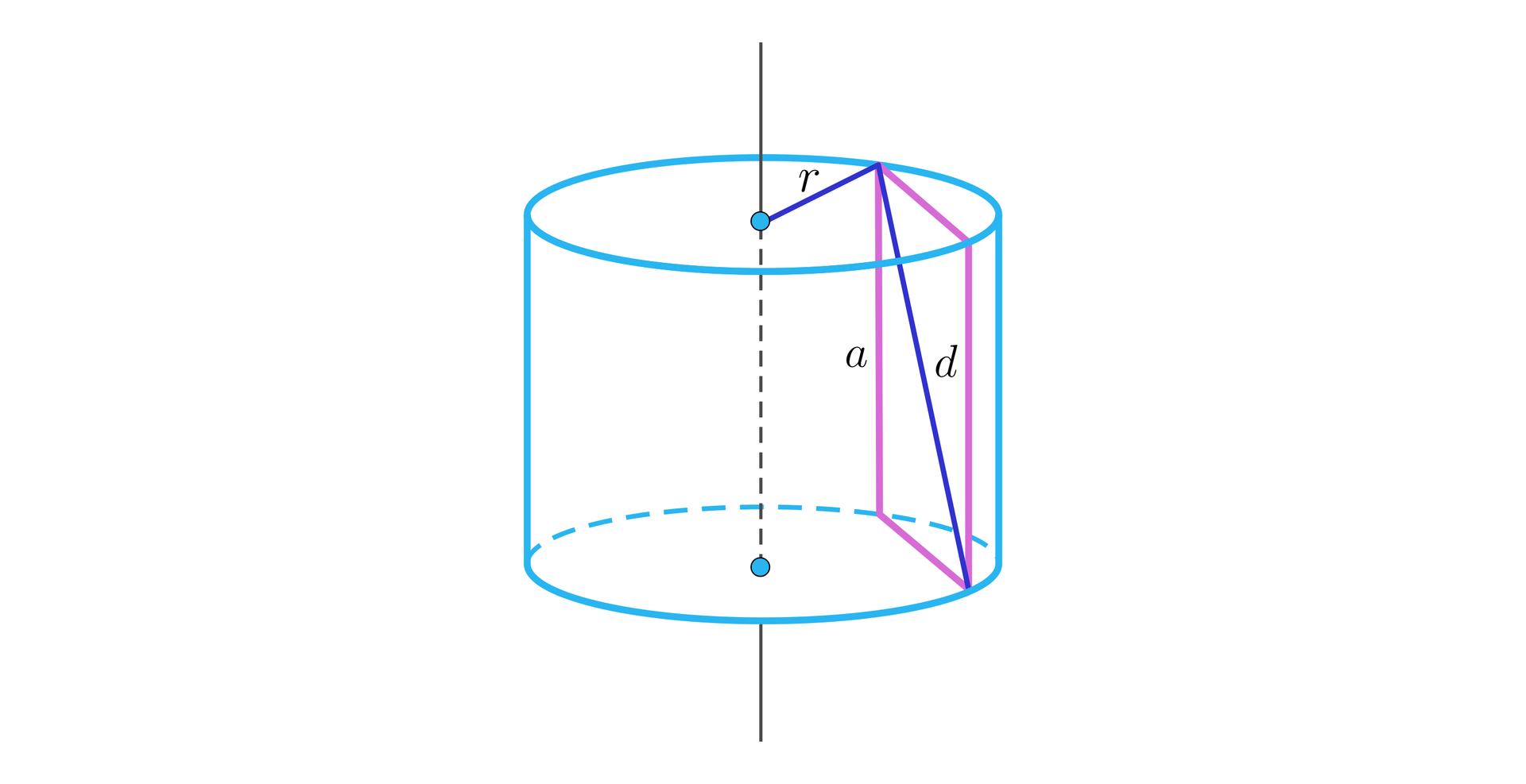
Do obliczenia pola powierzchni całkowitej walca musimy wyznaczyć długość promienia podstawy oraz wysokości walca.
Jeżeli przekrojem z rysunku jest kwadrat o przekątnej , to
, czyli .
Wobec tego wysokość walca jest równa .
Zauważmy, że odcinek, który jest odległością przekroju od osi symetrii walca, połowa długości boku kwadratu oraz promień podstawy walca tworzą trójkąt prostokątny, jak na poniższym rysunku.
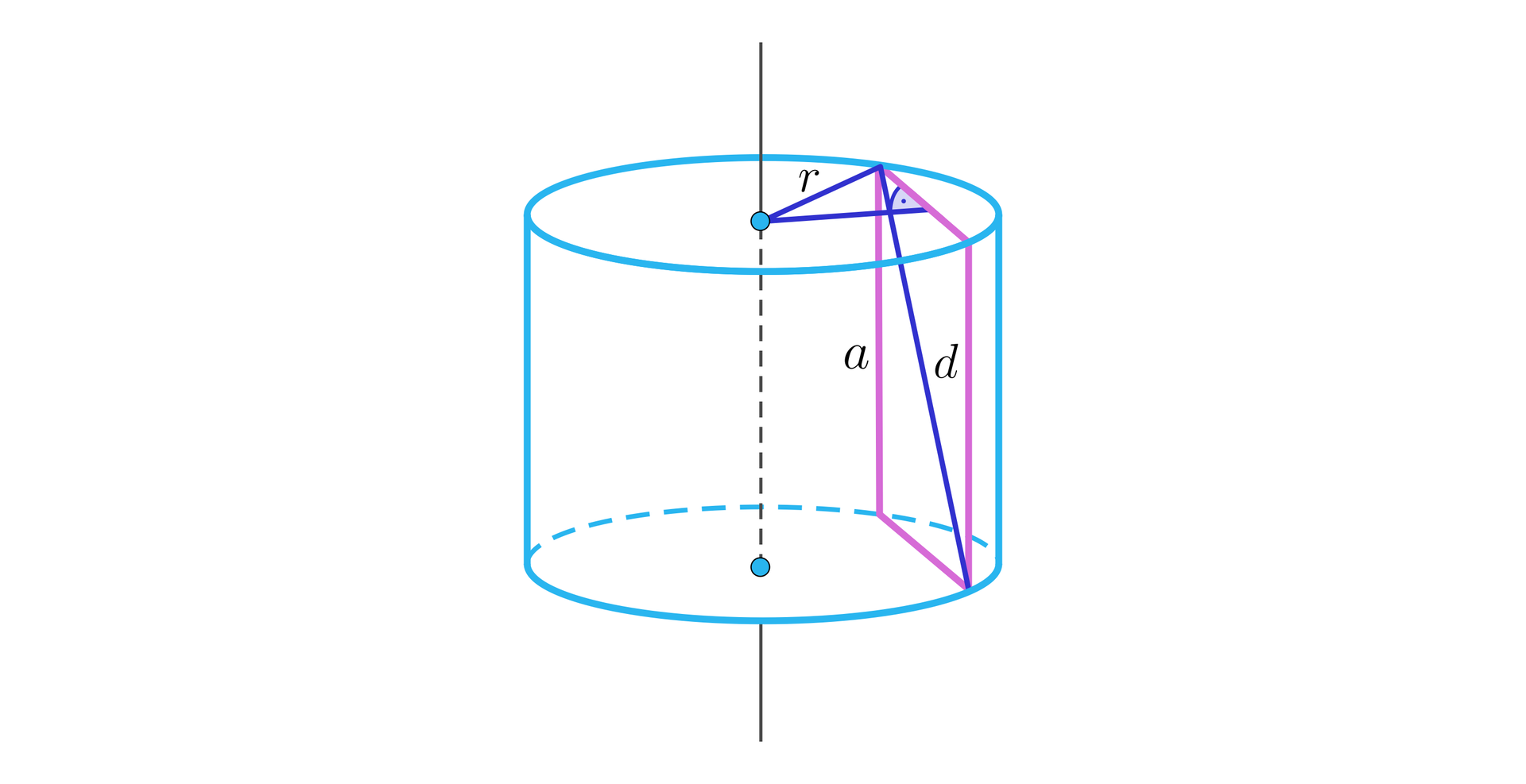
Zatem, korzystając z twierdzenia Pitagorasa, rozwiązujemy równanie:
, czyli .
Wysokość walca jest równa długości boku kwadratu, będącego przekrojem tego walca.
Zatem pole powierzchni całkowitej tego walca jest równe:
.
Średnica podstawy, wysokość oraz przekątna przekroju osiowego walca są kolejnymi liczbami parzystymi. Wyznaczymy pole powierzchni tego przekroju.
Rozwiązanie
Narysujmy walec i wprowadźmy oznaczenia, jak na rysunku.
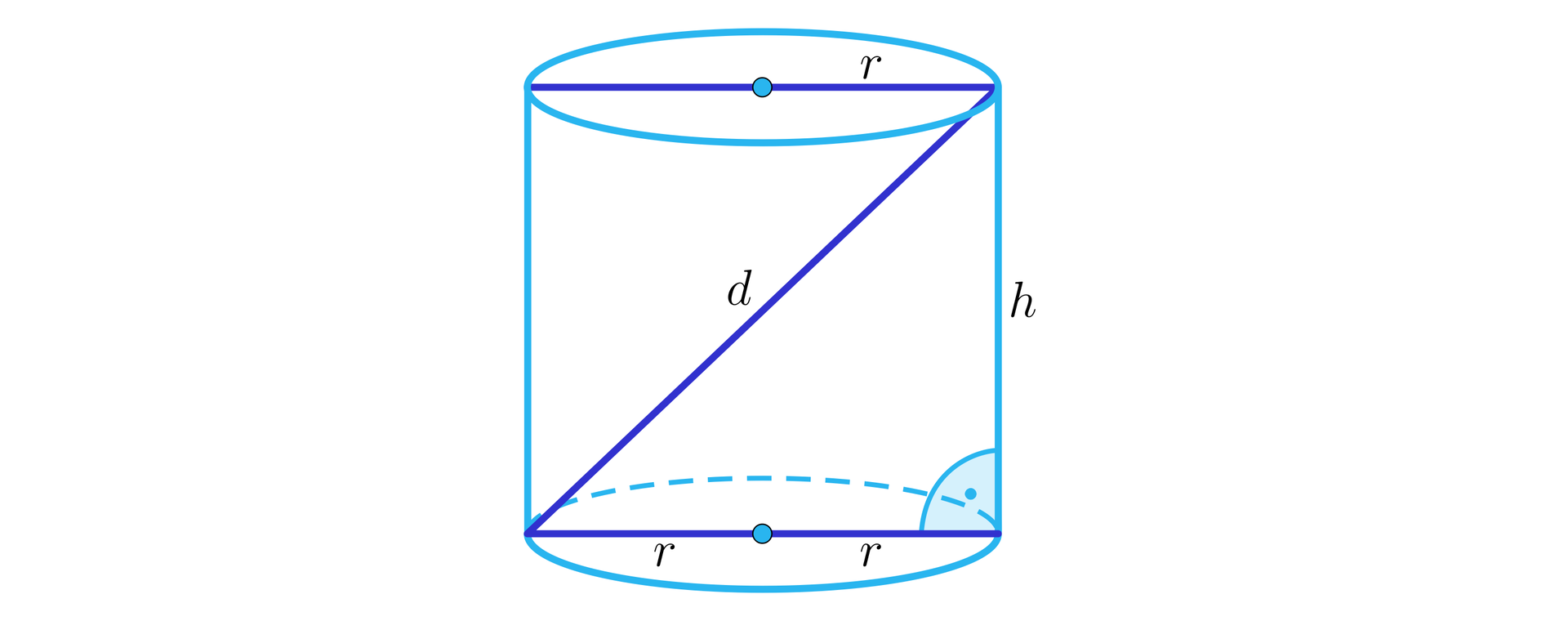
Ponieważ średnica podstawy, wysokość oraz przekątna przekroju osiowego walca są kolejnymi liczbami parzystymi, zatem:
,
.
Wielkości te tworzą trójkąt prostokątny, zatem do wyznaczenia wartości rozwiązujemy równanie:
.
Zatem
Zauważmy, że średnica podstawy, wysokość oraz przekątna przekroju osiowego walca są kolejnymi liczbami parzystymi, co spełnia warunki zadania.
Przekrojem walca jest prostokąt o bokach i , zatem jego pole jest równe:
.
Na podstawach walca poprowadzono dwie równoległe średnice. Przez przeciwległe końce tych średnic poprowadzono płaszczyznę styczną do okręgów, będących brzegami podstaw, jak na rysunku. Powstały w ten sposób przekrój walca jest elipsą, której pole jest razy większe od pola podstawy walca. Obliczymy objętość walca, jeżeli wiadomo, że wielka oś elipsy jest równa .
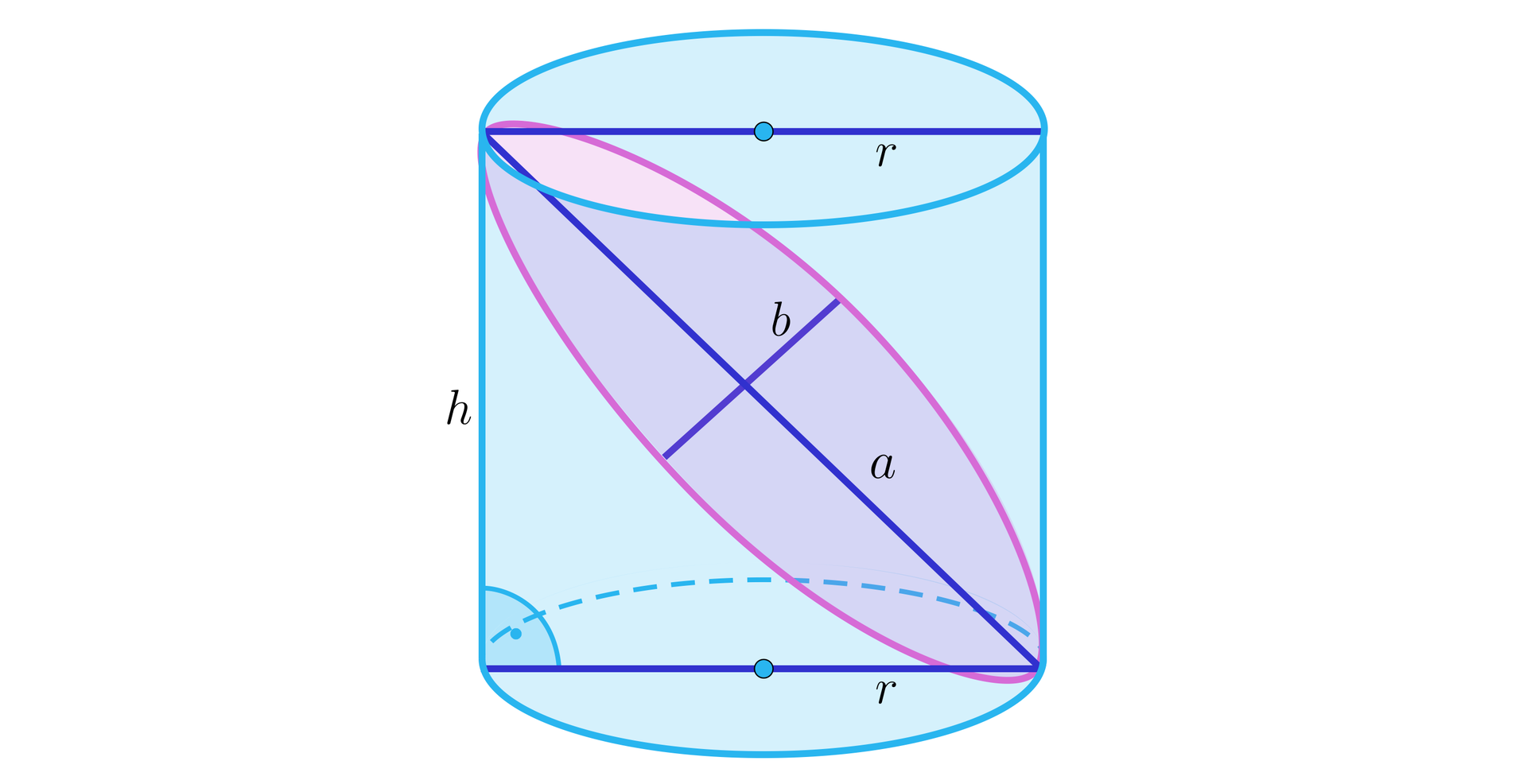
Rozwiązanie
Zauważmy, że mała półoś elipsy jest równa długości promienia podstawy walca, zatem .
Jeżeli , to .
Ponieważ pole elipsy obliczamy ze wzoru oraz to pole jest razy większe od pola podstawy walca, zatem:
, czyli .
Korzystając z twierdzenia Pitagorasa, obliczamy długość wysokości :
Zatem:
.
Słownik
bryła obrotowa, która powstaje przez obrót prostokąta dookoła osi zawierającej jeden z jego boków
zbiór punktów, dla których suma odległości od dwóch danych punktów, zwanych ogniskami, jest stała