Przeczytaj

Miejsce zerowe funkcji kwadratowej będziemy określać na różne sposoby:

poprzez odczytywanie z wykresu funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej,
z wykorzystaniem definicji miejsca zerowego,
z zastosowaniem wzorów na miejsca zerowe, w zależności od wartości wyróżnika funkcji kwadratowej.

Już wiesz

Miejscem zerowym funkcji nazywamy taki argument, dla którego wartość funkcji wynosi $0$ .

Graficznie miejsce zerowemiejsce zerowemiejsce zerowe funkcji określamy jako pierwszą współrzędną punktu przecięcia wykresu funkcji z poziomą osią $X$ .

Przykład 1

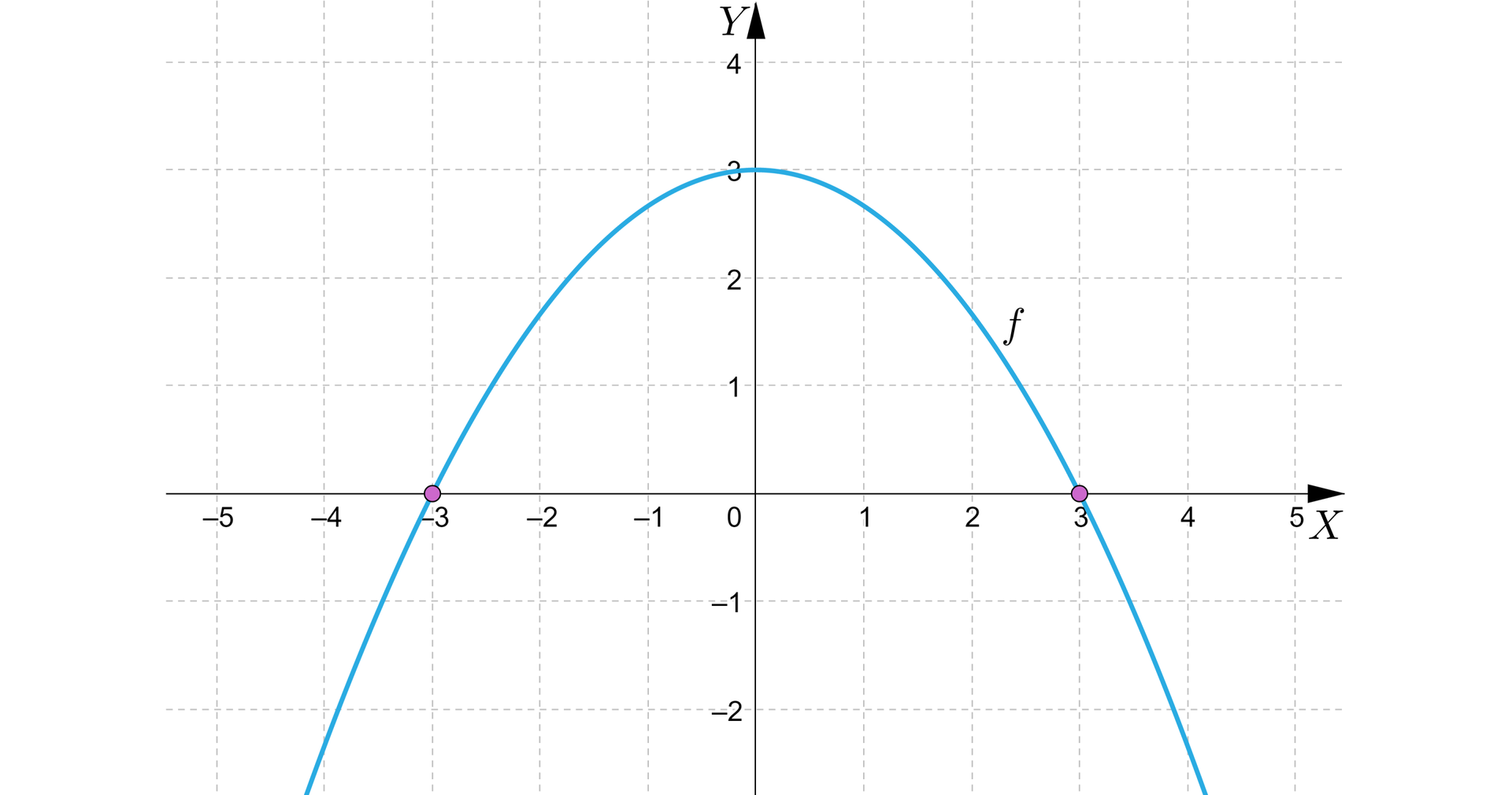
Odczytamy wartości miejsc zerowych z wykresu funkcji kwadratowej $f$ , której wykres przedstawiono na poniższym rysunku.

RM0vGOerVshu3

Ilustracja przedstawia układ współrzędnych z osią pionowa od minus 2 do czterech oraz osią poziomą od minus 5 do pięciu. Zaznaczono na nim parabolę z ramionami skierowanymi w dół oraz wierzchołkiem w punkcie 0;3. Funkcja posiada miejsca zerowe w punktach minus 3 oraz trzy.

Rozwiązanie:

Z wykresu odczytujemy, że miejscami zerowymi funkcji $f$ są liczby $(- 3)$ oraz $3$ .

Miejsca zerowe funkcji kwadratowej możemy wyznaczyć korzystając z równości $f (x) = 0$ .

Przykład 2

Wyznaczymy miejsca zerowe funkcji $f$ określonej wzorem:

a) $f (x) = x^{2} + 4 x$

Rozwiązanie:

Rozwiązujemy równanie $x^{2} + 4 x = 0$ , które zapisujemy w postaci $x (x + 4) = 0$ , zatem $x = 0$ lub $x = - 4$ .

Funkcja $f$ ma dwa miejsca zerowe $0$ oraz $(- 4)$ .

b) $f (x) = x^{2} - 9$

Rozwiązanie:

Rozwiązujemy równanie $x^{2} - 9 = 0$ , które zapisujemy w postaci $x^{2} = 9$ , zatem $x = - 3$ lub $x = 3$ .

Funkcja $f$ ma dwa miejsca zerowe $(- 3)$ oraz $3$ .

c) $f (x) = x^{2} - 6 x + 9$

Rozwiązanie:

Rozwiązujemy równanie $x^{2} - 6 x + 9 = 0$ , które przekształcamy do postaci ${(x - 3)}^{2} = 0$ , zatem $x - 3 = 0$ , czyli $x = 3$ .

Funkcja $f$ ma jedno miejsce zerowe $3$ .

d) $f (x) = x^{2} + 4 x + 3$

Rozwiązanie:

Rozwiązujemy równanie $x^{2} + 4 x + 3 = 0$ , które przekształcamy do postaci $x^{2} + 4 x + 4 - 1 = 0$ .

Zatem ${(x + 2)}^{2} = 1$ , czyli $x + 2 = 1$ lub $x + 2 = - 1$ .

Obliczamy, że $x = - 1$ lub $x = - 3$

Funkcja $f$ ma dwa miejsca zerowe $(- 1)$ oraz $(- 3)$ .

Jeżeli funkcja kwadratowa $f$ jest określona wzorem w postaci ogólnej $f (x) = a x^{2} + b x + c$ , gdzie $a \neq 0$ , to miejsca zerowe obliczamy w następujących krokach:

wypisujemy wartości współczynników $a$ , $b$ , $c$ ,
obliczamy $∆$ ,
wybieramy jedną z trzech poniższych możliwości.

Jeżeli:

$∆ > 0$ , to funkcja kwadratowa ma dwa miejsca zerowemiejsce zerowemiejsca zerowe: $x_{1} = \frac{- b - \sqrt{∆}}{2 a}$ oraz $x_{2} = \frac{- b + \sqrt{∆}}{2 a}$
$∆ = 0$ , to funkcja kwadratowa ma jedno miejsce zerowemiejsce zerowemiejsce zerowe: $x_{0} = \frac{- b}{2 a}$
$∆ < 0$ , to funkcja kwadratowa nie ma miejsc zerowych.

Przykład 3

Obliczymy miejsca zerowe funkcji kwadratowej $f$ określonej wzorem $f (x) = - x^{2} + x + 12$ .

Rozwiązanie:

Ponieważ $∆ = 1^{2} - 4 \cdot (- 1) \cdot 12 = 49 > 0$ , zatem funkcja $f$ ma dwa miejsca zerowe.

Wyznaczamy

$x_{1} = \frac{- 1 - \sqrt{49}}{2 \cdot (- 1)} = \frac{- 1 - 7}{- 2} = \frac{- 8}{- 2} = 4$

$x_{2} = \frac{- 1 + \sqrt{49}}{2 \cdot (- 1)} = \frac{- 1 + 7}{- 2} = \frac{6}{- 2} = - 3$

Miejscami zerowymi funkcji $f$ są liczby $4$ oraz $(- 3)$ .

Przykład 4

Obliczymy miejsca zerowe funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = {(x - 2)}^{2} - 4$ .

Rozwiązanie:

W celu wyznaczenia miejsc zerowych funkcji $f$ rozwiązujemy równanie:

${(x - 2)}^{2} - 4 = 0$

Równanie po przekształceniu zapisujemy w postaci ${(x - 2)}^{2} = 4$ .

Równanie to jest równoważne równaniom: $x - 2 = 2$ lub $x - 2 = - 2$ .

Funkcja $f$ ma dwa miejsca zerowe $0$ oraz $4$ .

Przykład 5

Wyznaczymy, dla jakiej wartości parametru $m$ funkcja kwadratowa $f$ określona wzorem $f (x) = - 3 x^{2} + (m - 2) x - 2$ ma miejsce zerowe równe $1$ .

Rozwiązanie:

Ponieważ liczba $1$ jest miejscem zerowym funkcji $f$ , więc $f (1) = 0$ .

Po podstawieniu $x = 1$ , otrzymujemy równanie: $0 = - 3 + (m - 2) - 2$ , z czego wynika że $m = 7$ .

Przykład 6

Wyznaczymy, dla jakiej wartości parametru $m$ funkcja kwadratowa $f$ określona wzorem $f (x) = 2 x^{2} + x + (m - 4)$ ma dwa miejsca zerowe.

Rozwiązanie:

Jeżeli $∆ > 0$ , to funkcja kwadratowa ma dwa miejsca zerowe.

Obliczamy $∆ = 1 - 4 \cdot 2 \cdot (m - 4) = 1 - 8 \cdot (m - 4) = 1 - 8 m + 32 = - 8 m + 33$ .

Zapisujemy warunek: $∆ > 0$ , stąd $- 8 m + 33 > 0$ .

Z tej nierówności wynika, że $m < \frac{33}{8}$ .

Przykład 7

Wyznaczymy, dla jakiej wartości parametru $m$ funkcja kwadratowa $f$ określona wzorem $f (x) = m x^{2} + 2 x + m$ ma dokładnie jedno miejsce zerowe.

Rozwiązanie:

Jeżeli $∆ = 0$ i $m \neq 0$ , to funkcja ma dokładnie jedno miejsce zerowe. Drugi z warunków musi być spełniony, bo z treści zadania wiemy, że funkcja ma być kwadratowa.

Zapisujemy warunek: $∆ = 0$ , stąd $4 - 4 m^{2} = 0$ . Z tego równania wynika, że $m = 1$ lub $m = - 1$ . Obie liczby są różne od zera, zatem spełniają warunki zadania.

Jeżeli wzór funkcji kwadratowej możemy zapisać za pomocą iloczynu czynników liniowych, to miejscami zerowymi funkcji $f$ określonej wzorem $f (x) = a (x - x_{1}) (x - x_{2})$ są liczby $x_{1}$ oraz $x_{2}$ .

Przykład 8

Wyznaczymy miejsca zerowe funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej $f$ określonej wzorem $f (x) = - 3 (x + 8) (x - 2)$ .

Rozwiązanie:

Miejscami zerowymi funkcji kwadratowej $f$ są liczby $x_{1} = - 8$ oraz $x_{2} = 2$ .

Jeżeli liczby $x_{1}$ oraz $x_{2}$ są miejscami zerowymi funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2} + b x + c$ , wówczas wartość współrzędnej $p$ wierzchołka paraboli, będącej wykresem funkcji $f$ możemy obliczyć ze wzoru:

p = \frac{x_{1} + x_{2}}{2}

Przykład 9

Wiadomo, że funkcja kwadratowa $f$ ma dwa miejsca zerowe. Obliczymy wartość drugiego miejsca zerowego, jeżeli jednym z miejsc zerowych funkcji $f$ jest liczba $(- 2)$ , zaś pierwsza współrzędna wierzchołka paraboli, która jest wykresem funkcji $f$ wynosi $p = 4$ .

Rozwiązanie:

Wprowadźmy oznaczenie: $x_{2}$ – drugie miejsce zerowe funkcji kwadratowej $f$ .

W celu wyznaczenia wartości tego miejsca zerowego, rozwiązujemy równanie:

$4 = \frac{- 2 + x_{2}}{2}$

Zatem $x_{2} = 10$ .

Słownik

miejsce zerowe

argument, dla którego wartość funkcji wynosi 0, pierwsza współrzędna punktu przecięcia wykresu funkcji z osią $X$

funkcja kwadratowa

funkcja określona za pomocą wzoru $f (x) = a x^{2} + b x + c$ , gdzie $a$ , $b$ , $c \in ℝ$ oraz $a \neq 0$

Wprowadzenie

Schemat interaktywny

Słownik