Przeczytaj

W tej sekcji znajdziesz przykłady implementacji reprezentacji grafów nieskierowanych bez wag oraz skierowanych bez wag w języku Java. Reprezentacje te zostały przedstawione w e‑materiale teoretycznymPpkZaFlK1e‑materiale teoretycznym, są to: macierz sąsiedztwa, lista sąsiedztwa, macierz incydencji.

Grafy nieskierowane

Macierz sąsiedztwa

Dany jest następujący graf spójny nieskierowany bez wag:

R1SLuEuzVC4ye

Ilustracja przedstawia pięciokąt wypukły. Jego wierzchołki są oznaczone kolejno cyframi 4, 0, 1, 2, 5. Wierzchołek 4 oraz 1 jest połączony przekątną, tak samo jak wierzchołek 2 i 0. Z wierzchołka 4 oraz 2 wychodzą proste, które spotykają się w punkcie oznaczonym 3, który znajduje się wewnątrz figury. Wszystkie wierzchołki i punkty są oznaczone niebieskimi kółkami. Odcinek łączący punkt 4 i 0 oznaczono jako e2, odcinek 0 i 1 oznaczono jako e0, odcinek 1 i 2 oznaczono e3, odcinek 5 i 2 oznaczono e6, odcinek 4 i 5 jako e8, odcinek 4 i 1 jako e4, odcinek 0 i 2 jako e1, odcinek 3 i 2 jako e5, odcinek 4 i 3 jako e7. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Macierz sąsiedztwa zaprezentowanego grafu nieskierowanego bez wag:

R12LrCWhJbLTN

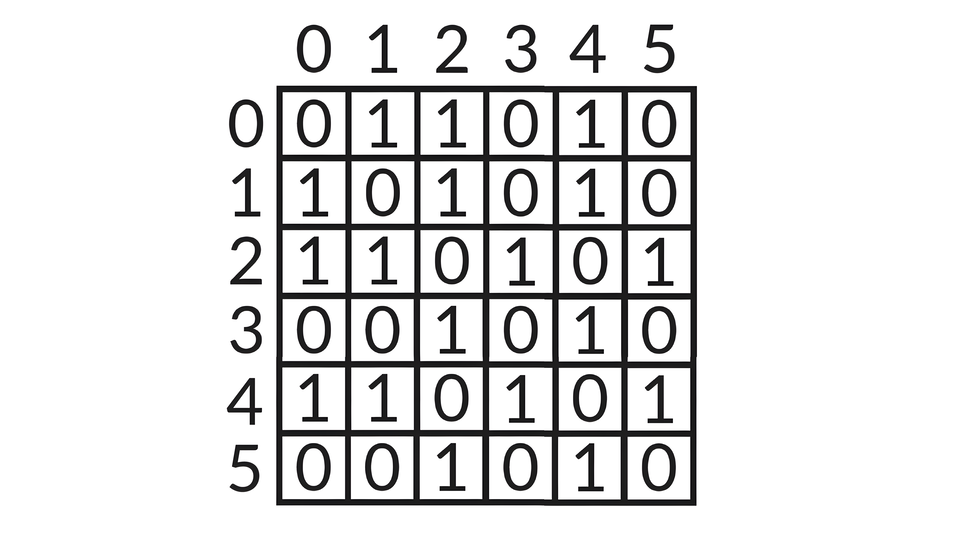
Ilustracja przedstawia tabelkę sześć na sześć kratek. Jej kolumny i rzędy są oznaczone cyframi od 0 do 5. W pierwszym rzędzie wpisano 0, 1, 1, 0, 1, 0, w drugim rzędzie 1, 0, 1, 0, 1, 0, w trzecim rzędzie, 1, 1, 0, 1, 0, 1, w czwartym rzędzie 0, 0, 1, 0, 1, 0, w piątym rzędzie 1, 1, 0, 1, 0, 1, w szóstym rzędzie 0, 0, 1, 0, 1, 0. — Macierz sąsiedztwa zaprezentowanego grafu.
Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Napiszmy teraz program. Na potrzeby implementacji macierz sąsiedztwa będzie dwuwymiarową tablicą o wyrazach typu int, o n wierszach i n kolumnach. Gdybyśmy chcieli rozpocząć od macierzy wypełnionej samymi zerami, wykorzystalibyśmy następujący aspekt języka Java:

Każda zmienna klasy, zmienna instancji lub składnik tablicy są inicjowane wartością domyślną podczas jej tworzenia. Dla typu int wartością domyślną jest zero, czyli 0.

Wystarczy zatem tylko zadeklarować operatorem new dwuwymiarową tablicę o n wierszach i n kolumnach.

int[][] macierzSasiedztwa = new int[n][n];

Dodawanie krawędzi wykonujemy za pomocą funkcji polaczWierzcholki(), do której przekazujemy trzy argumenty: macierzSasiedztwa oraz indeksy dwóch wierzchołków, które chcemy połączyć, czyli i razem z j.

static void polaczWierzcholki(int[][] macierzSasiedztwa, 
	int i, int j) {
	macierzSasiedztwa[i][j] = 1;
	macierzSasiedztwa[j][i] = 1;
}

Przykład 1

Przykład użycia takiej reprezentacji przedstawiony jest poniżej. Metoda wypisz() iteruje po każdym wierszu, a następnie po każdym wyrazie tego wiersza, wypisując macierz w konsoli. Ponieważ tablice w języku Java zawierają pole length, nie trzeba w naszym przykładzie definiować nowej zmiennej n przechowującej liczbę wierzchołków.

Linia 1. public class MacierzSasiedztwa otwórz nawias klamrowy. Linia 2. prawy ukośnik prawy ukośnik Metoda dodająca krawędź do grafu. Linia 3. static void polaczWierzcholki otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa przecinek int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 4. macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy znak równości 1 średnik. Linia 5. macierzSasiedztwa otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy znak równości 1 średnik. Linia 6. zamknij nawias klamrowy. Linia 8. prawy ukośnik prawy ukośnik Metoda wypisze macierz sąsiedztwa. Linia 9. static void wypisz otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 10. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny macierzSasiedztwa kropka length średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 11. for otwórz nawias okrągły int j znak równości 0 średnik j otwórz nawias ostrokątny macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy kropka length średnik j plus plus zamknij nawias okrągły. Linia 12. System kropka out kropka print otwórz nawias okrągły macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy plus cudzysłów cudzysłów zamknij nawias okrągły średnik. Linia 13. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 14. zamknij nawias klamrowy. Linia 15. zamknij nawias klamrowy. Linia 17. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 18. int n znak równości 6 średnik. Linia 19. int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa znak równości new int otwórz nawias kwadratowy n zamknij nawias kwadratowy otwórz nawias kwadratowy n zamknij nawias kwadratowy średnik. Linia 21. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 1 zamknij nawias okrągły średnik. Linia 22. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 2 zamknij nawias okrągły średnik. Linia 23. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 4 zamknij nawias okrągły średnik. Linia 24. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 1 przecinek 2 zamknij nawias okrągły średnik. Linia 25. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 1 przecinek 4 zamknij nawias okrągły średnik. Linia 26. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 2 przecinek 3 zamknij nawias okrągły średnik. Linia 27. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 2 przecinek 5 zamknij nawias okrągły średnik. Linia 28. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 3 przecinek 4 zamknij nawias okrągły średnik. Linia 29. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 4 przecinek 5 zamknij nawias okrągły średnik. Linia 31. System kropka out kropka println otwórz nawias okrągły cudzysłów Pierwotna postac dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 32. wypisz otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły średnik. Linia 33. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 35. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 36. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 5 zamknij nawias okrągły średnik. Linia 37. wypisz otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły średnik. Linia 38. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 40. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 41. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 2 przecinek 4 zamknij nawias okrągły średnik. Linia 42. wypisz otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły średnik. Linia 43. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 44. zamknij nawias klamrowy. Linia 45. zamknij nawias klamrowy.

public class MacierzSasiedztwa {
	// Metoda dodająca krawędź do grafu
	static void polaczWierzcholki(int[][] macierzSasiedztwa, int i, int j) {
		macierzSasiedztwa[i][j] = 1;
		macierzSasiedztwa[j][i] = 1;
	}
    
	// Metoda wypisze macierz sąsiedztwa
	static void wypisz(int[][] macierzSasiedztwa) {
		for (int i = 0; i < macierzSasiedztwa.length; i++) {
			for (int j = 0; j < macierzSasiedztwa[i].length; j++)
				System.out.print(macierzSasiedztwa[i][j] + " ");
			System.out.println();
		}
	}

	public static void main(String[] args) {
        int n = 6;
		int[][] macierzSasiedztwa = new int[n][n];

		polaczWierzcholki(macierzSasiedztwa, 0, 1);
		polaczWierzcholki(macierzSasiedztwa, 0, 2);
		polaczWierzcholki(macierzSasiedztwa, 0, 4);
		polaczWierzcholki(macierzSasiedztwa, 1, 2);
		polaczWierzcholki(macierzSasiedztwa, 1, 4);
		polaczWierzcholki(macierzSasiedztwa, 2, 3);
		polaczWierzcholki(macierzSasiedztwa, 2, 5);
		polaczWierzcholki(macierzSasiedztwa, 3, 4);
		polaczWierzcholki(macierzSasiedztwa, 4, 5);
        
		System.out.println("Pierwotna postac:");
		wypisz(macierzSasiedztwa);
		System.out.println();

		System.out.println("Po wywolaniu polaczWierzcholki(0, 5):");
		polaczWierzcholki(macierzSasiedztwa, 0, 5);
		wypisz(macierzSasiedztwa);
		System.out.println();
        
        System.out.println("Po wywolaniu polaczWierzcholki(2, 4):");
		polaczWierzcholki(macierzSasiedztwa, 2, 4);
		wypisz(macierzSasiedztwa);
		System.out.println();
	}
}

Wyjście programu:

Pierwotna postac:
0 1 1 0 1 0 
1 0 1 0 1 0 
1 1 0 1 0 1 
0 0 1 0 1 0 
1 1 0 1 0 1 
0 0 1 0 1 0 

Po wywolaniu polaczWierzcholki(0, 5):
0 1 1 0 1 1 
1 0 1 0 1 0 
1 1 0 1 0 1 
0 0 1 0 1 0 
1 1 0 1 0 1 
1 0 1 0 1 0 

Po wywolaniu polaczWierzcholki(2, 4):
0 1 1 0 1 1 
1 0 1 0 1 0 
1 1 0 1 1 1 
0 0 1 0 1 0 
1 1 1 1 0 1 
1 0 1 0 1 0

Lista sąsiedztwa

Lista sąsiedztwa zaprezentowanego grafu nieskierowanego bez wag:

Rri8wpXPrqHIU

Ilustracja przedstawia cyfry znajdujące się w ramkach. Każdy rząd oznaczony jest cyfrą od 0 do 5, która znajduje się w niebieskiej ramce, pozostałe ramki w rzędach są czarne. W pierwszym rzędzie oznaczonym cyfrą 0 w czarnych ramkach znajduje się cyfra 1, strzałka, cyfra 2, strzałka, cyfra 4. W drugim rzędzie oznaczonym cyfrą 1 znajdują się cyfry 0, 2, 4, w trzecim oznaczonym cyfrą 2 cyfry 0, 1, 3, 5, w czwartym rzędzie oznaczonym cyfrą 3 są cyfry 2, 4, w piątym rzędzie oznaczonym cyfrą 4 cyfry 0, 1, 3, 5, a w szóstym rzędzie oznaczonym cyfrą 5 cyfry 2, 4. Wszystkie liczby w rzędach są połączone strzałkami skierowanymi w prawo. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

W języku Java listę sąsiadów danego wierzchołka można zaimplementować z użyciem klasy LinkedList, która jest implementacją listy dwukierunkowej. LinkedList to klasa generycznatyp generycznyklasa generyczna z parametrem typu, zatem przy deklaracji zmiennej tej klasy musimy określić rodzaj przechowywanych elementów. W omawianym przypadku będziemy przechowywać zmienne typu int, więc deklaracja takiej listy sąsiadów będzie następująca:

LinkedList<Integer> listaSasiadow = new LinkedList<>();

Cała lista sąsiedztwa nie jest pojedynczą listą, lecz zestawem list sąsiadów każdego wierzchołka. Potrzebujemy zatem pewnego rodzaju kontenera na ten zestaw list.

Pomocna tu będzie kolekcja ArrayList. Klasa ta reprezentowana przez interfejs java.util.list pozwoli nam tworzyć tablice o zmiennym rozmiarze i to za jej pomocą zaimplementujemy listę sąsiedztwa. Jej główną przewagą nad klasyczną tablicą jest to, że programista nie musi przejmować się rozmiarem, jest ona bowiem automatycznie powiększana wraz z dodawaniem nowych elementów.

Podobnie jak LinkedList, także ArrayList jest klasą sparametryzowaną. Aby stworzyć listę tablicową o pojemności n przechowującą elementy typu LinkedList<Integer>, dodamy następująca deklarację:

ArrayList<LinkedList<Integer>> listaSasiedztwa = 
	new ArrayList<>(n);

Zmienna listaSasiedztwa o pojemności n została już zadeklarowana, ale nie zawiera jeszcze żadnej listy sąsiadów, musimy więc dla każdego wierzchołka stworzyć listę sąsiadów LinkedList i dodać ją do listy sąsiedztwa. Elementy do listy tablicowej ArrayList (podobnie jak LinkedList) dodajemy za pomocą metody add(). Nowy wyraz znajdzie się na końcu sekwencji.

for (int i = 0; i < n; i++) {
	listaSasiedztwa.add(new LinkedListInteger());
}

Do elementów listy tablicowej ArrayList nie dostaniemy się za pomocą nawiasów kwadratowych. Do tego celu ArrayList ma zdefiniowaną metodę get(). Aby uzyskać dostęp do elementu o indeksie i, do metody przekażemy zmienną i.

static void polaczWierzcholki(
	ArrayList<LinkedList<Integer>> listaSasiedztwa, 
	int i, int j) {
    
	listaSasiedztwa.get(i).add(j);
	listaSasiedztwa.get(j).add(i);
}

Przykład 2

Pełen kod wykorzystujący opisaną implementację znajduje się poniżej. Do iteracji po każdym elemencie listy dwukierunkowej użyto pętli zasięgu, która przy każdym kroku przekazuje zmiennej j wartość kolejnego elementu listy sąsiadów.

Linia 1. import java kropka util kropka ArrayList średnik. Linia 2. import java kropka util kropka LinkedList średnik. Linia 4. public class ListaSasiedztwa otwórz nawias klamrowy. Linia 5. static int n znak równości 6 średnik. Linia 7. prawy ukośnik prawy ukośnik Metoda dodająca krawędź do grafu. Linia 8. static void polaczWierzcholki otwórz nawias okrągły ArrayList otwórz nawias ostrokątny LinkedList otwórz nawias ostrokątny Integer zamknij nawias ostrokątny zamknij nawias ostrokątny listaSasiedztwa przecinek int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 9. listaSasiedztwa kropka get otwórz nawias okrągły i zamknij nawias okrągły kropka add otwórz nawias okrągły j zamknij nawias okrągły średnik. Linia 10. listaSasiedztwa kropka get otwórz nawias okrągły j zamknij nawias okrągły kropka add otwórz nawias okrągły i zamknij nawias okrągły średnik. Linia 11. zamknij nawias klamrowy. Linia 13. prawy ukośnik prawy ukośnik Metoda wypisze listę sąsiedztwa. Linia 14. static void wypisz otwórz nawias okrągły ArrayList otwórz nawias ostrokątny LinkedList otwórz nawias ostrokątny Integer zamknij nawias ostrokątny zamknij nawias ostrokątny listaSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 15. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny listaSasiedztwa kropka size otwórz nawias okrągły zamknij nawias okrągły średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 16. System kropka out kropka print otwórz nawias okrągły i plus cudzysłów dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 17. for otwórz nawias okrągły int j dwukropek listaSasiedztwa kropka get otwórz nawias okrągły i zamknij nawias okrągły zamknij nawias okrągły. Linia 18. System kropka out kropka print otwórz nawias okrągły j plus cudzysłów cudzysłów zamknij nawias okrągły średnik. Linia 19. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 20. zamknij nawias klamrowy. Linia 21. zamknij nawias klamrowy. Linia 23. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 24. ArrayList otwórz nawias ostrokątny LinkedList otwórz nawias ostrokątny Integer zamknij nawias ostrokątny zamknij nawias ostrokątny listaSasiedztwa znak równości new ArrayList otwórz nawias ostrokątny zamknij nawias ostrokątny otwórz nawias okrągły n zamknij nawias okrągły średnik. Linia 25. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły. Linia 26. listaSasiedztwa kropka add otwórz nawias okrągły new LinkedList otwórz nawias ostrokątny zamknij nawias ostrokątny otwórz nawias okrągły zamknij nawias okrągły zamknij nawias okrągły średnik. Linia 28. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 1 zamknij nawias okrągły średnik. Linia 29. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 2 zamknij nawias okrągły średnik. Linia 30. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 4 zamknij nawias okrągły średnik. Linia 31. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 1 przecinek 2 zamknij nawias okrągły średnik. Linia 32. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 1 przecinek 4 zamknij nawias okrągły średnik. Linia 33. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 2 przecinek 3 zamknij nawias okrągły średnik. Linia 34. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 2 przecinek 5 zamknij nawias okrągły średnik. Linia 35. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 3 przecinek 4 zamknij nawias okrągły średnik. Linia 36. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 4 przecinek 5 zamknij nawias okrągły średnik. Linia 38. System kropka out kropka println otwórz nawias okrągły cudzysłów Pierwotna postac dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 39. wypisz otwórz nawias okrągły listaSasiedztwa zamknij nawias okrągły średnik. Linia 40. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 42. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 43. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 5 zamknij nawias okrągły średnik. Linia 44. wypisz otwórz nawias okrągły listaSasiedztwa zamknij nawias okrągły średnik. Linia 45. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 47. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 48. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 2 przecinek 4 zamknij nawias okrągły średnik. Linia 49. wypisz otwórz nawias okrągły listaSasiedztwa zamknij nawias okrągły średnik. Linia 50. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 51. zamknij nawias klamrowy. Linia 52. zamknij nawias klamrowy.

import java.util.ArrayList;
import java.util.LinkedList;

public class ListaSasiedztwa {
	static int n = 6;

	// Metoda dodająca krawędź do grafu
	static void polaczWierzcholki(ArrayList<LinkedList<Integer>> listaSasiedztwa, int i, int j) {
		listaSasiedztwa.get(i).add(j);
		listaSasiedztwa.get(j).add(i);
	}

	// Metoda wypisze listę sąsiedztwa
	static void wypisz(ArrayList<LinkedList<Integer>> listaSasiedztwa) {
		for (int i = 0; i < listaSasiedztwa.size(); i++) {
			System.out.print(i + ": ");
			for (int j : listaSasiedztwa.get(i) )
				System.out.print(j + " ");
			System.out.println();
		}
	}

	public static void main(String[] args) {
		ArrayList<LinkedList<Integer>> listaSasiedztwa = new ArrayList<>(n);
		for (int i = 0; i < n; i++)
			listaSasiedztwa.add(new LinkedList<>());

		polaczWierzcholki(listaSasiedztwa, 0, 1);
		polaczWierzcholki(listaSasiedztwa, 0, 2);
		polaczWierzcholki(listaSasiedztwa, 0, 4);
		polaczWierzcholki(listaSasiedztwa, 1, 2);
		polaczWierzcholki(listaSasiedztwa, 1, 4);
		polaczWierzcholki(listaSasiedztwa, 2, 3);
		polaczWierzcholki(listaSasiedztwa, 2, 5);
		polaczWierzcholki(listaSasiedztwa, 3, 4);
		polaczWierzcholki(listaSasiedztwa, 4, 5);

		System.out.println("Pierwotna postac:");
		wypisz(listaSasiedztwa);
		System.out.println();
        
        System.out.println("Po wywolaniu polaczWierzcholki(0, 5):");
		polaczWierzcholki(listaSasiedztwa, 0, 5);
		wypisz(listaSasiedztwa);
		System.out.println();

		System.out.println("Po wywolaniu polaczWierzcholki(2, 4):");
		polaczWierzcholki(listaSasiedztwa, 2, 4);
		wypisz(listaSasiedztwa);
		System.out.println();
	}
}

Wyjście programu:

Pierwotna postac:
0: 1 2 4 
1: 0 2 4 
2: 0 1 3 5 
3: 2 4 4: 0 1 3 5 
5: 2 4 

Po wywolaniu polaczWierzcholki(0, 5):
0: 1 2 4 5 
1: 0 2 4 
2: 0 1 3 5 
3: 2 4 
4: 0 1 3 5 
5: 2 4 0 

Po wywolaniu polaczWierzcholki(2, 4):
0: 1 2 4 5 
1: 0 2 4 
2: 0 1 3 5 4 
3: 2 4 
4: 0 1 3 5 2 
5: 2 4 0

Macierz incydencji

Macierz incydencji zaprezentowanego grafu nieskierowanego bez wag:

R1QaZxcGv9w33

Ilustracja przedstawia tabelkę z dziewięcioma kolumnami i sześcioma rzędami. Kolumny są ponumerowane kolejno e0, e1, aż do e8, a rzędy od 0 do 5. W pierwszym rzędzie znajdują się następujące cyfry: 1, 1, 1, 0, 0, 0, 0, 0, 0, w drugim rzędzie 1, 0, 0, 1, 1, 0, 0, 0, 0, w trzecim rzędzie 0, 1, 0, 1, 0, 1, 1, 0, 0, w czwartym rzędzie 0, 0, 0, 0, 0, 1, 0, 1, 0, w piątym rzędzie 0, 0, 1, 0, 1, 0, 0, 1, 1, w szóstym rzędzie 0, 0, 0, 0, 0, 0, 1, 0, 1. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Macierz incydencji zdefiniujemy jako dwuwymiarową tablicę o n wierszach i maxM kolumnach. Zmienna maxM jest równa maksymalnej liczbie krawędzi dla grafu o n wierzchołkach. Jako że rozmiar macierzy incydencji zależy od liczby krawędzi, to w celu zapamiętania aktualnej liczby krawędzi zdefiniujemy nową zmienną m. Wartość ta będzie wskazywała, ile kolumn macierzy ma zostać wyświetlonych lub w którym miejscu należy wstawić nową krawędź.

int[][] macierzIncydencji = new int[n][maxM]

Na początku macierz będzie wypełniona zerami – nie ma potrzeby inicjowania tablicy. Dodawanie krawędzi odbywa się za pomocą funkcji polaczWierzcholki(), do której przekazujemy trzy argumenty: macierzIncydencji oraz indeksy dwóch wierzchołków, które chcemy połączyć, czyli i razem z j. Funkcja sprawdza, czy nie wykorzystaliśmy maksymalnej pojemności macierzy, a jeśli tak, to kończy swoje działanie. W przeciwnym wypadku następuje wpisanie jedynek odpowiednim wyrazom, po czym zmienna m zostaje zwiększona o 1.

static void polaczWierzcholki(int[][] macierzIncydencji, 
	int i, int j) {
	if (m >= maxM) return;
	macierzIncydencji[i][m] = 1;
	macierzIncydencji[j][m] = 1;
	m++;
}

Przykład 3

Pełen kod implementacji macierzy incydencji przedstawiony jest poniżej. Funkcja wypisz() iteruje tylko do wyrazu o indeksie m - 1, wypisując tym samym macierz o rozmiarze n na m.

Linia 1. public class MacierzIncydencji otwórz nawias klamrowy. Linia 2. static int n znak równości 6 średnik prawy ukośnik prawy ukośnik Stała liczba wierzchołków. Linia 3. static int maxM znak równości 15 średnik prawy ukośnik prawy ukośnik Maksymalna liczba krawędzi. Linia 4. private static int m znak równości 0 średnik prawy ukośnik prawy ukośnik Aktualna liczba krawędzi. Linia 6. prawy ukośnik prawy ukośnik Metoda dodająca krawędź do grafu. Linia 7. static void polaczWierzcholki otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzIncydencji przecinek int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 8. if otwórz nawias okrągły m zamknij nawias ostrokątny znak równości maxM zamknij nawias okrągły return średnik. Linia 9. macierzIncydencji otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy m zamknij nawias kwadratowy znak równości 1 średnik. Linia 10. macierzIncydencji otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias kwadratowy m zamknij nawias kwadratowy znak równości 1 średnik. Linia 11. m plus plus średnik. Linia 12. zamknij nawias klamrowy. Linia 14. prawy ukośnik prawy ukośnik Metoda macierz incydencji. Linia 15. static void wypisz otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzIncydencji zamknij nawias okrągły otwórz nawias klamrowy. Linia 16. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny macierzIncydencji kropka length średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 17. for otwórz nawias okrągły int j znak równości 0 średnik j otwórz nawias ostrokątny m średnik j plus plus zamknij nawias okrągły. Linia 18. System kropka out kropka print otwórz nawias okrągły macierzIncydencji otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy plus cudzysłów cudzysłów zamknij nawias okrągły średnik. Linia 19. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 20. zamknij nawias klamrowy. Linia 21. zamknij nawias klamrowy. Linia 23. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 24. int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzIncydencji znak równości new int otwórz nawias kwadratowy n zamknij nawias kwadratowy otwórz nawias kwadratowy maxM zamknij nawias kwadratowy średnik. Linia 26. prawy ukośnik prawy ukośnik Dodawanie początkowych krawędzi. Linia 27. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 1 zamknij nawias okrągły średnik. Linia 28. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 2 zamknij nawias okrągły średnik. Linia 29. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 4 zamknij nawias okrągły średnik. Linia 30. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 1 przecinek 2 zamknij nawias okrągły średnik. Linia 31. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 1 przecinek 4 zamknij nawias okrągły średnik. Linia 32. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 2 przecinek 3 zamknij nawias okrągły średnik. Linia 33. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 2 przecinek 5 zamknij nawias okrągły średnik. Linia 34. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 3 przecinek 4 zamknij nawias okrągły średnik. Linia 35. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 4 przecinek 5 zamknij nawias okrągły średnik. Linia 36. System kropka out kropka println otwórz nawias okrągły cudzysłów Pierwotna postac dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 37. wypisz otwórz nawias okrągły macierzIncydencji zamknij nawias okrągły średnik. Linia 38. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 40. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 41. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 5 zamknij nawias okrągły średnik. Linia 42. wypisz otwórz nawias okrągły macierzIncydencji zamknij nawias okrągły średnik. Linia 43. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 45. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 46. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 2 przecinek 4 zamknij nawias okrągły średnik. Linia 47. wypisz otwórz nawias okrągły macierzIncydencji zamknij nawias okrągły średnik. Linia 48. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 49. zamknij nawias klamrowy. Linia 50. zamknij nawias klamrowy.

public class MacierzIncydencji {
	static int n = 6; // Stała liczba wierzchołków
	static int maxM = 15; // Maksymalna liczba krawędzi
	private static int m = 0; // Aktualna liczba krawędzi

	// Metoda dodająca krawędź do grafu
	static void polaczWierzcholki(int[][] macierzIncydencji, int i, int j) {
		if (m >= maxM) return;
		macierzIncydencji[i][m] = 1;
		macierzIncydencji[j][m] = 1;
		m++;
	}

	// Metoda macierz incydencji
	static void wypisz(int[][] macierzIncydencji) {
		for (int i = 0; i < macierzIncydencji.length; i++) {
			for (int j = 0; j < m; j++) 
				System.out.print(macierzIncydencji[i][j] + " ");
			System.out.println();
		}
	}

	public static void main(String[] args) {
		int[][] macierzIncydencji = new int[n][maxM];

		// Dodawanie początkowych krawędzi
		polaczWierzcholki(macierzIncydencji, 0, 1);
		polaczWierzcholki(macierzIncydencji, 0, 2);
		polaczWierzcholki(macierzIncydencji, 0, 4);
		polaczWierzcholki(macierzIncydencji, 1, 2);
		polaczWierzcholki(macierzIncydencji, 1, 4);
		polaczWierzcholki(macierzIncydencji, 2, 3);
		polaczWierzcholki(macierzIncydencji, 2, 5);
		polaczWierzcholki(macierzIncydencji, 3, 4);
		polaczWierzcholki(macierzIncydencji, 4, 5);
		System.out.println("Pierwotna postac:");
		wypisz(macierzIncydencji);
		System.out.println();

		System.out.println("Po wywolaniu polaczWierzcholki(0, 5):");
		polaczWierzcholki(macierzIncydencji, 0, 5);
		wypisz(macierzIncydencji);
		System.out.println();
		
		System.out.println("Po wywolaniu polaczWierzcholki(2, 4):");
		polaczWierzcholki(macierzIncydencji, 2, 4);
		wypisz(macierzIncydencji);
		System.out.println();
	}
}

Wyjście programu:

Pierwotna postac:
1 1 1 0 0 0 0 0 0 
1 0 0 1 1 0 0 0 0 
0 1 0 1 0 1 1 0 0 
0 0 0 0 0 1 0 1 0 
0 0 1 0 1 0 0 1 1 
0 0 0 0 0 0 1 0 1 

Po wywolaniu polaczWierzcholki(0, 5):
1 1 1 0 0 0 0 0 0 1 
1 0 0 1 1 0 0 0 0 0 
0 1 0 1 0 1 1 0 0 0 
0 0 0 0 0 1 0 1 0 0 
0 0 1 0 1 0 0 1 1 0 
0 0 0 0 0 0 1 0 1 1 

Po wywolaniu polaczWierzcholki(2, 4):
1 1 1 0 0 0 0 0 0 1 0 
1 0 0 1 1 0 0 0 0 0 0 
0 1 0 1 0 1 1 0 0 0 1 
0 0 0 0 0 1 0 1 0 0 0 
0 0 1 0 1 0 0 1 1 0 1 
0 0 0 0 0 0 1 0 1 1 0

Grafy skierowane

Dany jest następujący graf spójny skierowany bez wag:

RAHN08vGLMRlZ

Na ilustracji znajduje się sześć oznaczonych na niebiesko punktów ponumerowanych od 0 do 5. Punkty 4, 0, 1, 2 i 5 tworzą wielokąt wypukły. Z punktu 0 do punktu 1 biegnie strzałka oznaczona e0, z punktu 0 do punktu 2 biegnie strzałka oznaczona e1, z punktu 0 do punktu 4 biegnie strzałka oznaczona e2, z punktu 1 do punktu 2 biegnie strzałka oznaczona e3, z punktu 1 do punktu 4 biegnie strzałka oznaczona e4, z punktu 2 do punktu 5 biegnie strzałka oznaczona e6, z punktu 2 do punktu 3 znajdującego się wewnątrz wielokątu jest oznaczone e5, z punktu 3 do punktu 4 biegnie strzałka oznaczona e7, punkt 4 i 5 łączy odcinek zakończony strzałkami oznaczony e8 i e9. — Źródło: Contentplus.pl Sp. z o.o., Contentplus, licencja: CC BY-SA 3.0.

Macierz sąsiedztwa

Macierz sąsiedztwa zaprezentowanego grafu skierowanego bez wag:

RLvIuveWgLRIR

Ilustracja przedstawia tabelkę z sześcioma kolumnami i sześcioma rzędami. Kolumny są ponumerowane kolejno od 0 do 5, a rzędy od 0 do 5. W pierwszym rzędzie znajdują się następujące cyfry: 0, 1, 1, 0, 1, 0, w drugim rzędzie 0, 0, 1, 0, 1, 0, w trzecim rzędzie 0, 0, 0, 1, 0, 1, w czwartym rzędzie 0, 0, 0, 0, 1, 0, w piątym rzędzie 0, 0, 0, 0, 0, 1, w szóstym rzędzie 0, 0, 0, 0, 1, 0. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Przejdźmy do implementacji programu.

Deklarujemy operatorem new dwuwymiarową tablicę o n wierszach i n kolumnach.

int[][] macierzSasiedztwa = new int[n][n];

Dodajemy krawędzie za pomocą funkcji polaczWierzcholki(), do której przekazujemy trzy argumenty: macierzSasiedztwa oraz indeksy dwóch wierzchołków, które chcemy połączyć, czyli i razem z j.

Zwróć uwagę na to, że w przypadku grafów skierowanych znaczenie ma kierunek krawędzi. Dodawana krawędź zaczyna się w wierzchołku i, natomiast kończy w wierzchołku j. Dlatego w przypadku macierzy sąsiedztwa element o indeksach [i][j] przyjmuje wartość 1, natomiast element o indeksach [j][i] przyjmuje wartość 0.

static void polaczWierzcholki(int[][] macierzSasiedztwa, 
	int i, int j) {
	macierzSasiedztwa[i][j] = 1;
	macierzSasiedztwa[j][i] = 0;
}

Przykład 4

Zapoznajmy się z przykładem użycia takiej reprezentacji.

Linia 1. public class MacierzSasiedztwa otwórz nawias klamrowy. Linia 2. prawy ukośnik prawy ukośnik Metoda dodająca krawędź do grafu. Linia 3. static void polaczWierzcholki otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa przecinek int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 4. macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy znak równości 1 średnik. Linia 5. macierzSasiedztwa otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias kwadratowy i zamknij nawias kwadratowy znak równości 0 średnik. Linia 6. zamknij nawias klamrowy. Linia 8. prawy ukośnik prawy ukośnik Metoda wypisze macierz sąsiedztwa. Linia 9. static void wypisz otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 10. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny macierzSasiedztwa kropka length średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 11. for otwórz nawias okrągły int j znak równości 0 średnik j otwórz nawias ostrokątny macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy kropka length średnik j plus plus zamknij nawias okrągły. Linia 12. System kropka out kropka print otwórz nawias okrągły macierzSasiedztwa otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy plus cudzysłów cudzysłów zamknij nawias okrągły średnik. Linia 13. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 14. zamknij nawias klamrowy. Linia 15. zamknij nawias klamrowy. Linia 17. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 18. int n znak równości 6 średnik. Linia 19. int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzSasiedztwa znak równości new int otwórz nawias kwadratowy n zamknij nawias kwadratowy otwórz nawias kwadratowy n zamknij nawias kwadratowy średnik. Linia 21. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 1 zamknij nawias okrągły średnik. Linia 22. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 2 zamknij nawias okrągły średnik. Linia 23. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 4 zamknij nawias okrągły średnik. Linia 24. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 1 przecinek 2 zamknij nawias okrągły średnik. Linia 25. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 1 przecinek 4 zamknij nawias okrągły średnik. Linia 26. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 2 przecinek 3 zamknij nawias okrągły średnik. Linia 27. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 2 przecinek 5 zamknij nawias okrągły średnik. Linia 28. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 3 przecinek 4 zamknij nawias okrągły średnik. Linia 29. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 4 przecinek 5 zamknij nawias okrągły średnik. Linia 30. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 5 przecinek 4 zamknij nawias okrągły średnik. Linia 32. System kropka out kropka println otwórz nawias okrągły cudzysłów Pierwotna postac dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 33. wypisz otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły średnik. Linia 34. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 36. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 37. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 0 przecinek 5 zamknij nawias okrągły średnik. Linia 38. wypisz otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły średnik. Linia 39. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 41. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 42. polaczWierzcholki otwórz nawias okrągły macierzSasiedztwa przecinek 2 przecinek 4 zamknij nawias okrągły średnik. Linia 43. wypisz otwórz nawias okrągły macierzSasiedztwa zamknij nawias okrągły średnik. Linia 44. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 45. zamknij nawias klamrowy. Linia 46. zamknij nawias klamrowy.

public class MacierzSasiedztwa {
	// Metoda dodająca krawędź do grafu
	static void polaczWierzcholki(int[][] macierzSasiedztwa, int i, int j) {
		macierzSasiedztwa[i][j] = 1;
		macierzSasiedztwa[j][i] = 0;
	}
    
	// Metoda wypisze macierz sąsiedztwa
	static void wypisz(int[][] macierzSasiedztwa) {
		for (int i = 0; i < macierzSasiedztwa.length; i++) {
			for (int j = 0; j < macierzSasiedztwa[i].length; j++)
				System.out.print(macierzSasiedztwa[i][j] + " ");
			System.out.println();
		}
	}

	public static void main(String[] args) {
        int n = 6;
		int[][] macierzSasiedztwa = new int[n][n];

		polaczWierzcholki(macierzSasiedztwa, 0, 1);
		polaczWierzcholki(macierzSasiedztwa, 0, 2);
		polaczWierzcholki(macierzSasiedztwa, 0, 4);
		polaczWierzcholki(macierzSasiedztwa, 1, 2);
		polaczWierzcholki(macierzSasiedztwa, 1, 4);
		polaczWierzcholki(macierzSasiedztwa, 2, 3);
		polaczWierzcholki(macierzSasiedztwa, 2, 5);
		polaczWierzcholki(macierzSasiedztwa, 3, 4);
		polaczWierzcholki(macierzSasiedztwa, 4, 5);
        polaczWierzcholki(macierzSasiedztwa, 5, 4);
        
		System.out.println("Pierwotna postac:");
		wypisz(macierzSasiedztwa);
		System.out.println();

		System.out.println("Po wywolaniu polaczWierzcholki(0, 5):");
		polaczWierzcholki(macierzSasiedztwa, 0, 5);
		wypisz(macierzSasiedztwa);
		System.out.println();
        
        System.out.println("Po wywolaniu polaczWierzcholki(2, 4):");
		polaczWierzcholki(macierzSasiedztwa, 2, 4);
		wypisz(macierzSasiedztwa);
		System.out.println();
	}
}

Wyjście programu:

Pierwotna postac:
0 1 1 0 1 0 
0 0 1 0 1 0 
0 0 0 1 0 1 
0 0 0 0 1 0 
0 0 0 0 0 0 
0 0 0 0 1 0 

Po wywolaniu polaczWierzcholki(0, 5):
0 1 1 0 1 1 
0 0 1 0 1 0 
0 0 0 1 0 1 
0 0 0 0 1 0 
0 0 0 0 0 0 
0 0 0 0 1 0 
    
Po wywolaniu polaczWierzcholki(2, 4):
0 1 1 0 1 1 
0 0 1 0 1 0 
0 0 0 1 1 1 
0 0 0 0 1 0 
0 0 0 0 0 0 
0 0 0 0 1 0

Lista sąsiedztwa

Lista sąsiedztwa zaprezentowanego grafu skierowanego bez wag:

R12MBK6iNvSjP

Ilustracja przedstawia cyfry znajdujące się w ramkach. Każdy rząd oznaczony jest od 0 do 5, a dana cyfra znajduje się w niebieskiej ramce pozostałe ramki są czarne. Wszystkie liczby w rzędach w czarnych ramkach są połączone strzałkami skierowanymi w prawo. W pierwszym rzędzie znajduje się 1 strzałka 2 strzałka 4, w drugim rzędzie znajduje się 2 strzałka 4, w trzecim 3 strzałka 5, w czwartym rzędzie 4, w piątym rzędzie 5, w szóstym rzędzie 4. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Implementujemy listę sąsiadów wierzchołka:

LinkedList<Integer> listaSasiadow = new LinkedList<>();

Ponieważ cała lista sąsiedztwa nie jest pojedynczą listą, a zestawem list, ponownie wykorzystamy kolekcję ArrayList.

Tworzymy listę tablicową o pojemności n przechowującą elementy typu LinkedList<Integer>:

ArrayList<LinkedList<Integer>> listaSasiedztwa = 
	new ArrayList<>(n);

Dotychczas zadeklarowaliśmy zmienną listaSasiedztwa o pojemności n, nie zawiera ona jednak jeszcze żadnej listy sąsiadów. Dla każdego wierzchołka tworzymy listę sąsiadów LinkedList i dodajemy ją do listy sąsiedztwa. Do listy tablicowej ArrayList (podobnie jak LinkedList) elementy dodajemy za pomocą metody add(). Nowy wyraz znajdzie się na końcu sekwencji.

for (int i = 0; i < n; i++) {
	listaSasiedztwa.add(new LinkedListInteger());
}

Aby dostać się do elementów listy tablicowej ArrayList, zastosujemy metodę get(). Aby uzyskać dostęp do elementu o indeksie i, do metody przekażemy zmienną j.

Element o indeksie i to wierzchołek, w którym zaczyna się krawędź. Zmienna j przechowuje informację na temat wierzchołka, w którym krawędź się kończy (zgodnie z jej kierunkiem).

static void polaczWierzcholki(
	ArrayList<LinkedList<Integer>> listaSasiedztwa, 
	int i, int j) {
    
	listaSasiedztwa.get(i).add(j);
}

Przykład 5

Prześledźmy kod, w którym zastosowano opisaną implementację.

Linia 1. import java kropka util kropka ArrayList średnik. Linia 2. import java kropka util kropka LinkedList średnik. Linia 4. public class ListaSasiedztwa otwórz nawias klamrowy. Linia 5. static int n znak równości 6 średnik. Linia 7. prawy ukośnik prawy ukośnik Metoda dodająca krawędź do grafu. Linia 8. static void polaczWierzcholki otwórz nawias okrągły ArrayList otwórz nawias ostrokątny LinkedList otwórz nawias ostrokątny Integer zamknij nawias ostrokątny zamknij nawias ostrokątny listaSasiedztwa przecinek int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 9. listaSasiedztwa kropka get otwórz nawias okrągły i zamknij nawias okrągły kropka add otwórz nawias okrągły j zamknij nawias okrągły średnik. Linia 10. zamknij nawias klamrowy. Linia 12. prawy ukośnik prawy ukośnik Metoda wypisze listę sąsiedztwa. Linia 13. static void wypisz otwórz nawias okrągły ArrayList otwórz nawias ostrokątny LinkedList otwórz nawias ostrokątny Integer zamknij nawias ostrokątny zamknij nawias ostrokątny listaSasiedztwa zamknij nawias okrągły otwórz nawias klamrowy. Linia 14. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny listaSasiedztwa kropka size otwórz nawias okrągły zamknij nawias okrągły średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 15. System kropka out kropka print otwórz nawias okrągły i plus cudzysłów dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 16. for otwórz nawias okrągły int j dwukropek listaSasiedztwa kropka get otwórz nawias okrągły i zamknij nawias okrągły zamknij nawias okrągły. Linia 17. System kropka out kropka print otwórz nawias okrągły j plus cudzysłów cudzysłów zamknij nawias okrągły średnik. Linia 18. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 19. zamknij nawias klamrowy. Linia 20. zamknij nawias klamrowy. Linia 22. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 23. ArrayList otwórz nawias ostrokątny LinkedList otwórz nawias ostrokątny Integer zamknij nawias ostrokątny zamknij nawias ostrokątny listaSasiedztwa znak równości new ArrayList otwórz nawias ostrokątny zamknij nawias ostrokątny otwórz nawias okrągły n zamknij nawias okrągły średnik. Linia 24. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny n średnik i plus plus zamknij nawias okrągły. Linia 25. listaSasiedztwa kropka add otwórz nawias okrągły new LinkedList otwórz nawias ostrokątny zamknij nawias ostrokątny otwórz nawias okrągły zamknij nawias okrągły zamknij nawias okrągły średnik. Linia 27. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 1 zamknij nawias okrągły średnik. Linia 28. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 2 zamknij nawias okrągły średnik. Linia 29. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 4 zamknij nawias okrągły średnik. Linia 30. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 1 przecinek 2 zamknij nawias okrągły średnik. Linia 31. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 1 przecinek 4 zamknij nawias okrągły średnik. Linia 32. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 2 przecinek 3 zamknij nawias okrągły średnik. Linia 33. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 2 przecinek 5 zamknij nawias okrągły średnik. Linia 34. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 3 przecinek 4 zamknij nawias okrągły średnik. Linia 35. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 4 przecinek 5 zamknij nawias okrągły średnik. Linia 36. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 5 przecinek 4 zamknij nawias okrągły średnik. Linia 38. System kropka out kropka println otwórz nawias okrągły cudzysłów Pierwotna postac dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 39. wypisz otwórz nawias okrągły listaSasiedztwa zamknij nawias okrągły średnik. Linia 40. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 42. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 43. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 0 przecinek 5 zamknij nawias okrągły średnik. Linia 44. wypisz otwórz nawias okrągły listaSasiedztwa zamknij nawias okrągły średnik. Linia 45. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 47. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 48. polaczWierzcholki otwórz nawias okrągły listaSasiedztwa przecinek 2 przecinek 4 zamknij nawias okrągły średnik. Linia 49. wypisz otwórz nawias okrągły listaSasiedztwa zamknij nawias okrągły średnik. Linia 50. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 51. zamknij nawias klamrowy. Linia 52. zamknij nawias klamrowy.

import java.util.ArrayList;
import java.util.LinkedList;

public class ListaSasiedztwa {
	static int n = 6;

	// Metoda dodająca krawędź do grafu
	static void polaczWierzcholki(ArrayList<LinkedList<Integer>> listaSasiedztwa, int i, int j) {
		listaSasiedztwa.get(i).add(j);
	}

	// Metoda wypisze listę sąsiedztwa
	static void wypisz(ArrayList<LinkedList<Integer>> listaSasiedztwa) {
		for (int i = 0; i < listaSasiedztwa.size(); i++) {
			System.out.print(i + ": ");
			for (int j : listaSasiedztwa.get(i) )
				System.out.print(j + " ");
			System.out.println();
		}
	}

	public static void main(String[] args) {
		ArrayList<LinkedList<Integer>> listaSasiedztwa = new ArrayList<>(n);
		for (int i = 0; i < n; i++)
			listaSasiedztwa.add(new LinkedList<>());

		polaczWierzcholki(listaSasiedztwa, 0, 1);
		polaczWierzcholki(listaSasiedztwa, 0, 2);
		polaczWierzcholki(listaSasiedztwa, 0, 4);
		polaczWierzcholki(listaSasiedztwa, 1, 2);
		polaczWierzcholki(listaSasiedztwa, 1, 4);
		polaczWierzcholki(listaSasiedztwa, 2, 3);
		polaczWierzcholki(listaSasiedztwa, 2, 5);
		polaczWierzcholki(listaSasiedztwa, 3, 4);
		polaczWierzcholki(listaSasiedztwa, 4, 5);
		polaczWierzcholki(listaSasiedztwa, 5, 4);

		System.out.println("Pierwotna postac:");
		wypisz(listaSasiedztwa);
		System.out.println();
        
        System.out.println("Po wywolaniu polaczWierzcholki(0, 5):");
		polaczWierzcholki(listaSasiedztwa, 0, 5);
		wypisz(listaSasiedztwa);
		System.out.println();

		System.out.println("Po wywolaniu polaczWierzcholki(2, 4):");
		polaczWierzcholki(listaSasiedztwa, 2, 4);
		wypisz(listaSasiedztwa);
		System.out.println();
	}
}

Wyjście programu:

Pierwotna postac:
0: 1 2 4 
1: 2 4 
2: 3 5 
3: 4 
4: 5 
5: 4 

Po wywolaniu polaczWierzcholki(0, 5):
0: 1 2 4 5 
1: 2 4 
2: 3 5 
3: 4 
4: 5 
5: 4 

Po wywolaniu polaczWierzcholki(2, 4):
0: 1 2 4 5 
1: 2 4 
2: 3 5 4 
3: 4 
4: 5 
5: 4

Macierz incydencji

Macierz incydencji zaprezentowanego grafu skierowanego bez wag:

R18PudLdMOJKJ

Ilustracja przedstawia tabelkę z dziesięcioma kolumnami i sześcioma rzędami. Kolumny są ponumerowane kolejno e0, e1, aż do e9, a rzędy od 0 do 5. W pierwszym rzędzie znajdują się następujące cyfry: 1, 1, 1, 0, 0, 0, 0, 0, 0, 0 w drugim rzędzie -1, 0, 0, 1, 1, 0, 0, 0, 0, 0, w trzecim rzędzie 0, -1, 0, -1, 0, 1, 1, 0, 0, 0, w czwartym rzędzie 0, 0, 0, 0, 0, -1, 0, 1, 0, 0, w piątym rzędzie 0, 0, -1, 0, -1, 0, 0, -1, 1, -1, w szóstym rzędzie 0, 0, 0, 0, 0, 0, -1, 0, -1, 1. — Źródło: Contentplus.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Definiujemy macierz incydencji jako dwuwymiarową tablicę o n wierszach i maxM kolumnach.

int[][] macierzIncydencji = new int[n][maxM]

Początkowo macierz będzie wypełniona zerami, więc nie musimy inicjować tablicy.

Dodajemy krawędzie, używając funkcji polaczWierzcholki(), do której przekazujemy trzy argumenty: macierzIncydencji oraz indeksy dwóch wierzchołków, które chcemy połączyć, czyli i razem z j. Funkcja weryfikuje, czy nie wykorzystaliśmy maksymalnej pojemności macierzy. Jeśli tak – kończymy działanie funkcji. Jeśli nie, w przypadku tej reprezentacji, wierzchołkowi i przypisujemy wartość 1 (tam krawędź się zaczyna), natomiast wierzchołkowi, w którym się kończy (zgodnie z kierunkiem krawędzi) przypisujemy wartość -1.

static void polaczWierzcholki(int[][] macierzIncydencji, 
	int i, int j) {
	if (m >= maxM) return;
	macierzIncydencji[i][m] = 1;
	macierzIncydencji[j][m] = -1;
	m++;
}

Przykład 6

Przeanalizujmy kod implementacji macierzy incydencji.

Linia 1. public class MacierzIncydencji otwórz nawias klamrowy. Linia 2. static int n znak równości 6 średnik prawy ukośnik prawy ukośnik Stała liczba wierzchołków. Linia 3. static int maxM znak równości 15 średnik prawy ukośnik prawy ukośnik Maksymalna liczba krawędzi. Linia 4. private static int m znak równości 0 średnik prawy ukośnik prawy ukośnik Aktualna liczba krawędzi. Linia 6. prawy ukośnik prawy ukośnik Metoda dodająca krawędź do grafu. Linia 7. static void polaczWierzcholki otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzIncydencji przecinek int i przecinek int j zamknij nawias okrągły otwórz nawias klamrowy. Linia 8. if otwórz nawias okrągły m zamknij nawias ostrokątny znak równości maxM zamknij nawias okrągły return średnik. Linia 9. macierzIncydencji otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy m zamknij nawias kwadratowy znak równości 1 średnik. Linia 10. macierzIncydencji otwórz nawias kwadratowy j zamknij nawias kwadratowy otwórz nawias kwadratowy m zamknij nawias kwadratowy znak równości minus 1 średnik. Linia 11. m plus plus średnik. Linia 12. zamknij nawias klamrowy. Linia 14. prawy ukośnik prawy ukośnik Metoda macierz incydencji. Linia 15. static void wypisz otwórz nawias okrągły int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzIncydencji zamknij nawias okrągły otwórz nawias klamrowy. Linia 16. for otwórz nawias okrągły int i znak równości 0 średnik i otwórz nawias ostrokątny macierzIncydencji kropka length średnik i plus plus zamknij nawias okrągły otwórz nawias klamrowy. Linia 17. for otwórz nawias okrągły int j znak równości 0 średnik j otwórz nawias ostrokątny m średnik j plus plus zamknij nawias okrągły. Linia 18. System kropka out kropka print otwórz nawias okrągły macierzIncydencji otwórz nawias kwadratowy i zamknij nawias kwadratowy otwórz nawias kwadratowy j zamknij nawias kwadratowy plus cudzysłów lewy ukośnik t cudzysłów zamknij nawias okrągły średnik. Linia 19. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 20. zamknij nawias klamrowy. Linia 21. zamknij nawias klamrowy. Linia 23. public static void main otwórz nawias okrągły String otwórz nawias kwadratowy zamknij nawias kwadratowy args zamknij nawias okrągły otwórz nawias klamrowy. Linia 24. int otwórz nawias kwadratowy zamknij nawias kwadratowy otwórz nawias kwadratowy zamknij nawias kwadratowy macierzIncydencji znak równości new int otwórz nawias kwadratowy n zamknij nawias kwadratowy otwórz nawias kwadratowy maxM zamknij nawias kwadratowy średnik. Linia 26. prawy ukośnik prawy ukośnik Dodawanie początkowych krawędzi. Linia 27. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 1 zamknij nawias okrągły średnik. Linia 28. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 2 zamknij nawias okrągły średnik. Linia 29. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 4 zamknij nawias okrągły średnik. Linia 30. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 1 przecinek 2 zamknij nawias okrągły średnik. Linia 31. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 1 przecinek 4 zamknij nawias okrągły średnik. Linia 32. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 2 przecinek 3 zamknij nawias okrągły średnik. Linia 33. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 2 przecinek 5 zamknij nawias okrągły średnik. Linia 34. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 3 przecinek 4 zamknij nawias okrągły średnik. Linia 35. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 4 przecinek 5 zamknij nawias okrągły średnik. Linia 36. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 5 przecinek 4 zamknij nawias okrągły średnik. Linia 37. System kropka out kropka println otwórz nawias okrągły cudzysłów Pierwotna postac dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 38. wypisz otwórz nawias okrągły macierzIncydencji zamknij nawias okrągły średnik. Linia 39. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 41. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 0 przecinek 5 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 42. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 0 przecinek 5 zamknij nawias okrągły średnik. Linia 43. wypisz otwórz nawias okrągły macierzIncydencji zamknij nawias okrągły średnik. Linia 44. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 46. System kropka out kropka println otwórz nawias okrągły cudzysłów Po wywolaniu polaczWierzcholki otwórz nawias okrągły 2 przecinek 4 zamknij nawias okrągły dwukropek cudzysłów zamknij nawias okrągły średnik. Linia 47. polaczWierzcholki otwórz nawias okrągły macierzIncydencji przecinek 2 przecinek 4 zamknij nawias okrągły średnik. Linia 48. wypisz otwórz nawias okrągły macierzIncydencji zamknij nawias okrągły średnik. Linia 49. System kropka out kropka println otwórz nawias okrągły zamknij nawias okrągły średnik. Linia 50. zamknij nawias klamrowy. Linia 51. zamknij nawias klamrowy.

public class MacierzIncydencji {
	static int n = 6; // Stała liczba wierzchołków
	static int maxM = 15; // Maksymalna liczba krawędzi
	private static int m = 0; // Aktualna liczba krawędzi

	// Metoda dodająca krawędź do grafu
	static void polaczWierzcholki(int[][] macierzIncydencji, int i, int j) {
		if (m >= maxM) return;
		macierzIncydencji[i][m] = 1;
		macierzIncydencji[j][m] = -1;
		m++;
	}

	// Metoda macierz incydencji
	static void wypisz(int[][] macierzIncydencji) {
		for (int i = 0; i < macierzIncydencji.length; i++) {
			for (int j = 0; j < m; j++) 
				System.out.print(macierzIncydencji[i][j] + "\t");
			System.out.println();
		}
	}

	public static void main(String[] args) {
		int[][] macierzIncydencji = new int[n][maxM];

		// Dodawanie początkowych krawędzi
		polaczWierzcholki(macierzIncydencji, 0, 1);
		polaczWierzcholki(macierzIncydencji, 0, 2);
		polaczWierzcholki(macierzIncydencji, 0, 4);
		polaczWierzcholki(macierzIncydencji, 1, 2);
		polaczWierzcholki(macierzIncydencji, 1, 4);
		polaczWierzcholki(macierzIncydencji, 2, 3);
		polaczWierzcholki(macierzIncydencji, 2, 5);
		polaczWierzcholki(macierzIncydencji, 3, 4);
		polaczWierzcholki(macierzIncydencji, 4, 5);
        polaczWierzcholki(macierzIncydencji, 5, 4);
		System.out.println("Pierwotna postac:");
		wypisz(macierzIncydencji);
		System.out.println();

		System.out.println("Po wywolaniu polaczWierzcholki(0, 5):");
		polaczWierzcholki(macierzIncydencji, 0, 5);
		wypisz(macierzIncydencji);
		System.out.println();
		
		System.out.println("Po wywolaniu polaczWierzcholki(2, 4):");
		polaczWierzcholki(macierzIncydencji, 2, 4);
		wypisz(macierzIncydencji);
		System.out.println();
	}
}

Wyjście programu:

Pierwotna postac:
1	1	1	0	0	0	0	0	0	0	
-1	0	0	1	1	0	0	0	0	0	
0	-1	0	-1	0	1	1	0	0	0	
0	0	0	0	0	-1	0	1	0	0	
0	0	-1	0	-1	0	0	-1	1	-1	
0	0	0	0	0	0	-1	0	-1	1	

Po wywolaniu polaczWierzcholki(0, 5):
1	1	1	0	0	0	0	0	0	0	1	
-1	0	0	1	1	0	0	0	0	0	0	
0	-1	0	-1	0	1	1	0	0	0	0	
0	0	0	0	0	-1	0	1	0	0	0	
0	0	-1	0	-1	0	0	-1	1	-1	0	
0	0	0	0	0	0	-1	0	-1	1	-1	

Po wywolaniu polaczWierzcholki(2, 4):
1	1	1	0	0	0	0	0	0	0	1	0	
-1	0	0	1	1	0	0	0	0	0	0	0	
0	-1	0	-1	0	1	1	0	0	0	0	1	
0	0	0	0	0	-1	0	1	0	0	0	0	
0	0	-1	0	-1	0	0	-1	1	-1	0	-1	
0	0	0	0	0	0	-1	0	-1	1	-1	0

Słownik

graf

struktura składająca się z niepustego zbioru wierzchołków oraz rodziny krawędzi; dla grafu G zbiór wierzchołków oznaczamy $V (G)$ (ang. verticies – wierzchołki), a rodzinę krawędzi – $E (G)$ (ang. edges – krawędzie); liczbę elementów zbioru $V (G)$ oznaczamy literą $n$ ; liczbę elementów rodziny $E (G)$ – $m$

graf spójny

graf, którego nie można przedstawić w postaci sumy dwóch grafów

graf ważony

graf którego krawędzie mają przypisane wagi

krawędź

nieuporządkowana para (niekoniecznie różnych) elementów zbioru wierzchołków

incydencja

relacja między wierzchołkami a łączącą je krawędzią grafu; mówimy, że dwa sąsiednie wierzchołki połączone pewną krawędzią są incydentne z tą krawędzią

izomorfizm

właściwość grafów polegająca na tym, że między grafami występuje wzajemnie jednoznaczna odpowiedniość wierzchołków; liczba krawędzi łączących dane dwa wierzchołki jednego grafu jest równa liczbie krawędzi łączących odpowiadające im wierzchołki drugiego grafu

lista sąsiedztwa

zestaw $| V |$ uporządkowanych list, gdzie lista o indeksie $i$ jest listą wszystkich sąsiadów wierzchołka $i$

macierz

dwuwymiarowa tablica elementów (zwykle liczbowych), licząca $n$ wierszy i $m$ kolumn

macierz incydencji

macierz zerojedynkowa $M$ rozmiaru $| V | \times | E |$ , dla której każda krawędź grafu musi mieć unikatowy indeks; wyraz $m_{i,e}$ jest równy $1$ , o ile krawędź o indeksie $e$ jest incydentna do wierzchołka $i$

macierz sąsiedztwa

macierz zerojedynkowa $A$ rozmiaru $| V | \times | V |$ , w której wyraz $a_{i,j}$ jest równy $1$ , jeśli wierzchołki $i$ oraz $j$ są sąsiednie, a $0$ w przeciwnym przypadku; macierz sąsiedztwa jest symetryczna dla grafów nieskierowanych

stopień wierzchołka

liczba krawędzi incydentnych z danym wierzchołkiem

typ generyczny

klasa lub interfejs sparametryzowany względem typów podanych przy deklaracji; do określenia parametrów typu używamy nawiasów ostrych (<>); typy generyczne umożliwiają napisanie ogólnej definicji, która działa z różnymi typami, pozwalając tym samym na ponowne użycie kodu bez konieczności definiowania nowych definicji klas lub interfejsu działających na innym typie zmiennych

waga krawędzi

wartość przypisana krawędzi grafu

wierzchołek

element należący do zbioru wierzchołków

Wprowadzenie

Film samouczek

Grafy nieskierowane

Macierz sąsiedztwa

Lista sąsiedztwa

Macierz incydencji

Grafy skierowane

Macierz sąsiedztwa

Lista sąsiedztwa

Macierz incydencji

Słownik