Przeczytaj

W materiale omówimy, w jaki sposób odczytuje się lub wyznacza wartości dodatnie oraz wartości ujemne funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej a także wyznaczymy argumenty, dla których te wartości są przyjmowane.

Już wiesz

Jeżeli wierzchołkiem paraboli, będącej wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2} + b x + c$ , gdzie $a \neq 0$ , jest punkt o współrzędnych $(p, q)$ , to:

dla $a > 0$ zbiorem wartościzbiór wartości funkcjizbiorem wartości funkcji jest przedział $⟨q, \infty)$ ,
dla $a < 0$ zbiorem wartościzbiór wartości funkcjizbiorem wartości funkcji jest przedział $(- \infty, q⟩$ .

Do wyznaczenia wartości dodatnich oraz wartości ujemnych funkcji kwadratowej posłużymy się wzorem lub wykresem.

Argumenty funkcji, których wartości są równe $0$ , odpowiadają pierwszym współrzędnym punktów należących do paraboli, będącej wykresem tej funkcji kwadratowej. Punkty te leżą na osi $X$ .

Jeżeli funkcja kwadratowa ma miejsca zerowe, to:

funkcja ta przyjmuje wartości dodatnie dla argumentów będących odciętymi punktów wykresu tej funkcji, które leżą powyżej osi $X$ . Druga współrzędna tych punktów jest dodatnia;
funkcja ta przyjmuje wartości ujemne dla argumentów będących odciętymi punktów wykresu tej funkcji, które leżą poniżej tej osi. Druga współrzędna tych punktów jest ujemna.

W przypadku określania wartości ujemnych oraz wartości dodatnich funkcji kwadratowej możemy wyróżnić następujące możliwości:

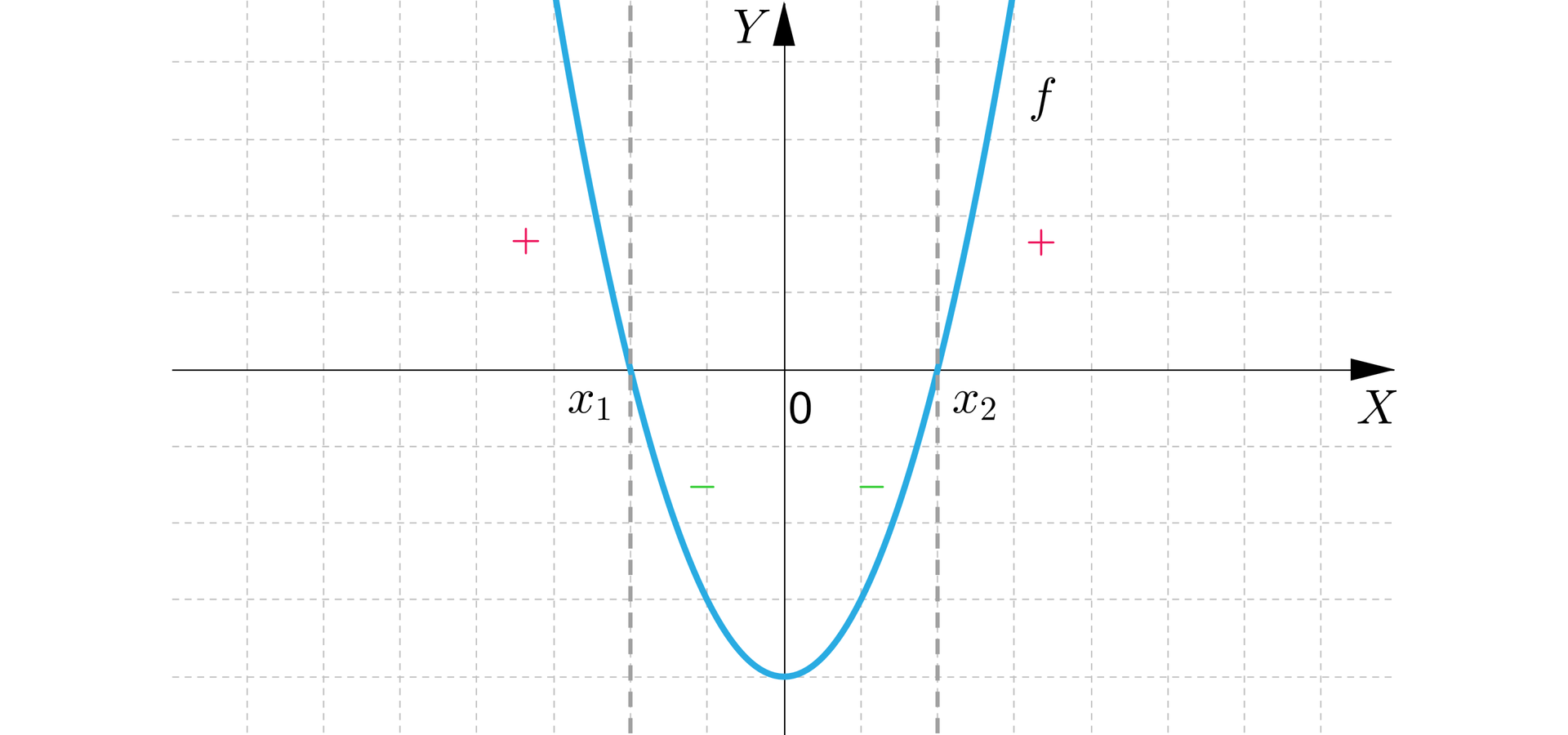
I. Jeżeli ramiona paraboli, która jest wykresem funkcji kwadratowej, są skierowane do góry, $q$ jest drugą współrzędną wierzchołka paraboli, funkcja ma dwa miejsca zerowe $x_{1}$ i $x_{2}$ oraz $x_{1} < x_{2}$ , to:

funkcja przyjmuje wartości ujemne należące do przedziału $⟨q, 0)$ dla $x \in (x_{1}, x_{2})$ ,
funkcja przyjmuje wartości dodatnie należące do przedziału $(0, \infty)$ dla $x \in (- \infty, x_{1}) \cup (x_{2}, \infty)$ .

R16vOSOrZbswH

Ilustracja przedstawia poziomą oś X oraz pionową oś Y. Na rysunku zaznaczono także wykres funkcji kwadratowej będącą parabolą z ramionami skierowanymi do góry i z wierzchołkiem zawierającym się w pionowej osi Y pod osią X. Wykres funkcji ma dwa miejsca zerowe, pierwsze w punkcie nawias x indeks dolny jeden koniec indeksu średnik zero koniec nawiasu oraz drugie w punkcie nawias x indeks dolny dwa koniec indeksu średnik zero koniec nawiasu.

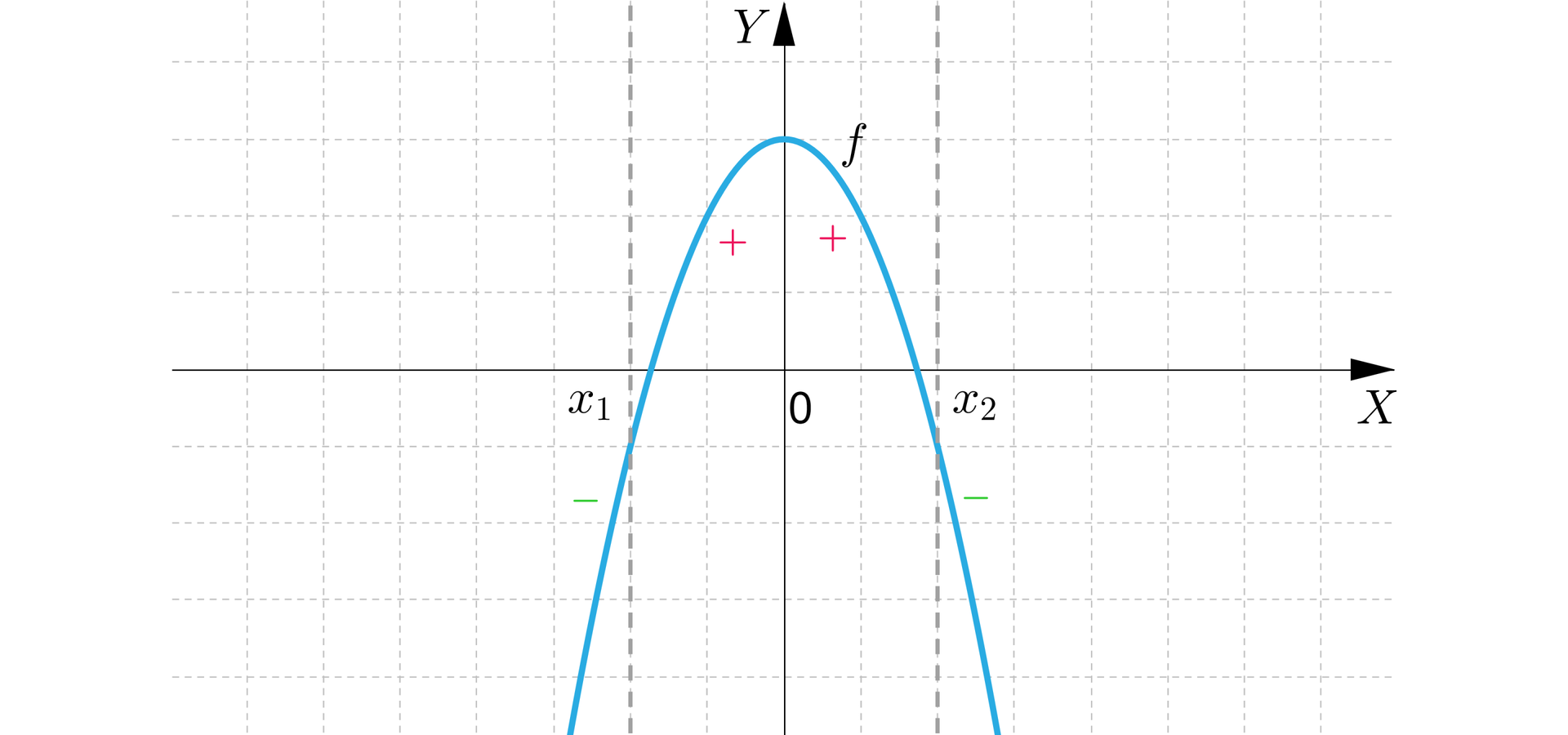
II. Jeżeli ramiona paraboli, która jest wykresem funkcji kwadratowej, są skierowane do dołu, $q$ jest drugą współrzędną wierzchołka paraboli, funkcja ma dwa miejsca zerowe $x_{1}$ i $x_{2}$ oraz $x_{1} < x_{2}$ , to:

funkcja przyjmuje wartości dodatnie należące do przedziału $(0, q⟩$ dla $x \in (x_{1}, x_{2})$ ,
funkcja przyjmuje wartości ujemne należące do przedziału $(- \infty, 0)$ dla $x \in (- \infty, x_{1}) \cup (x_{2}, \infty)$ .

RJo2s5dP0deu7

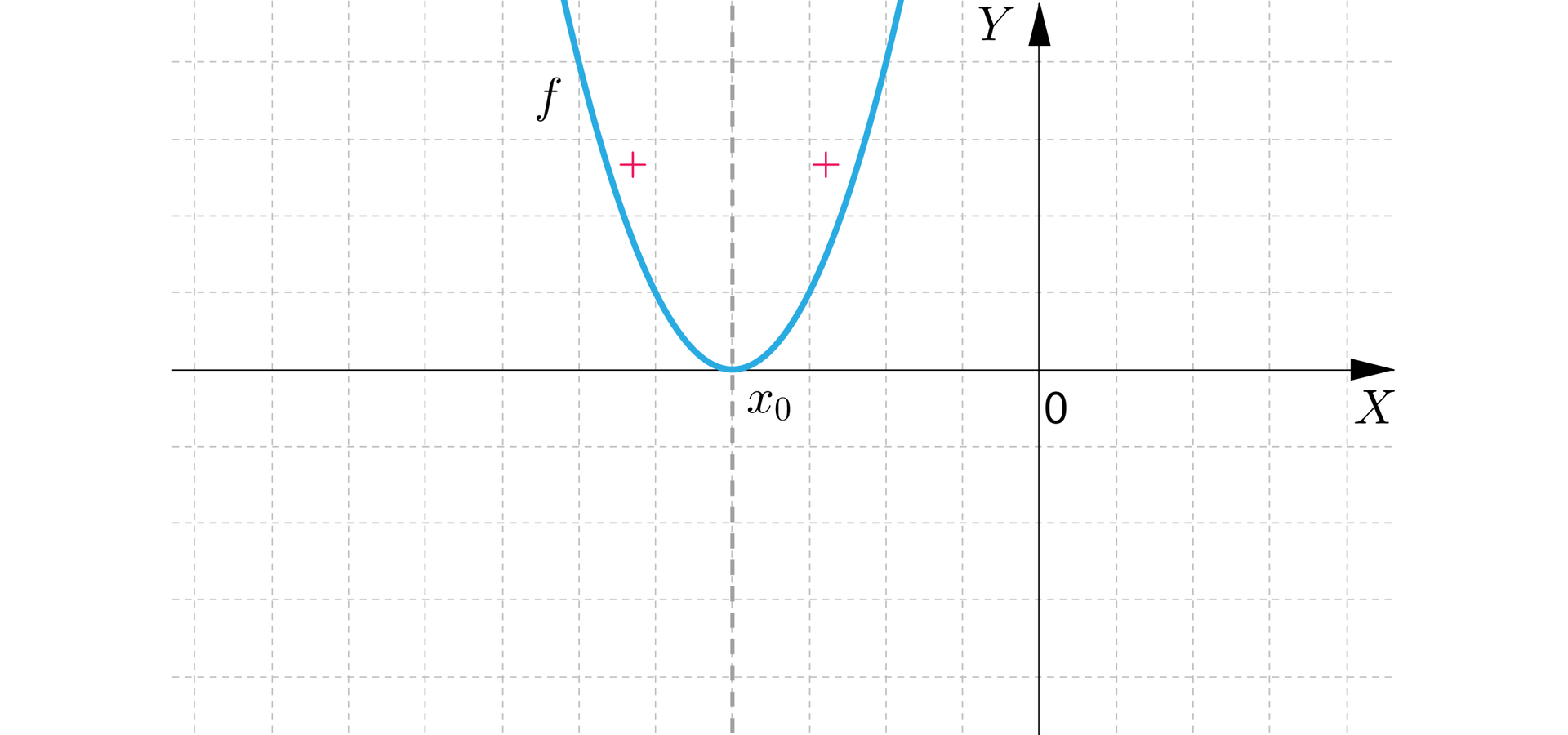
III. Jeżeli ramiona paraboli, która jest wykresem funkcji kwadratowej, są skierowane do góry, $q$ jest drugą współrzędną wierzchołka paraboli, funkcja ma jedno miejsce zerowe $x_{0}$ , to:

funkcja przyjmuje tylko wartości dodatnie należące do przedziału $(0, \infty)$ dla $x \in (- \infty, x_{0}) \cup (x_{0}, \infty)$ .

R1LFT4jOD7lfo

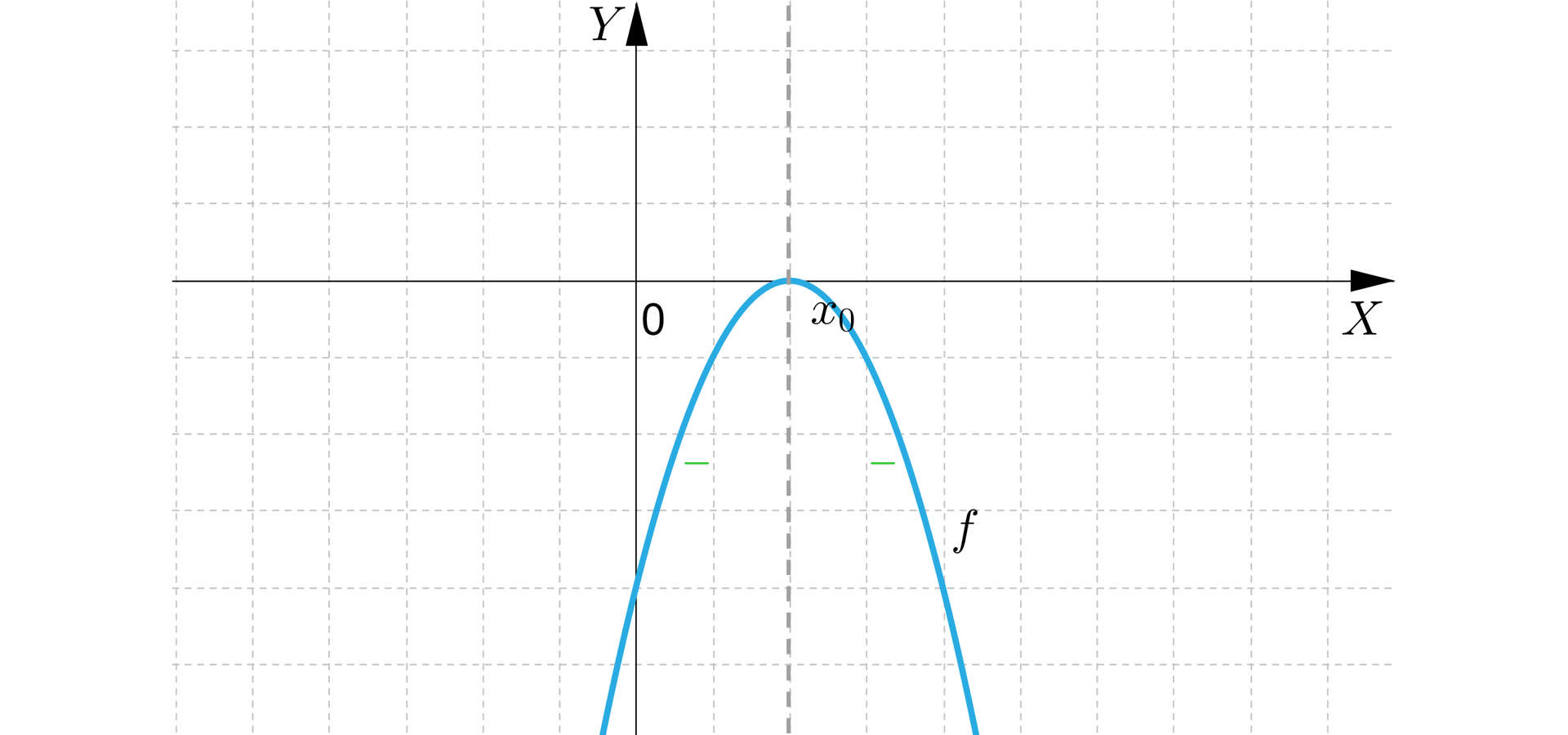
IV. Jeżeli ramiona paraboli, która jest wykresem funkcji kwadratowej, są skierowane do dołu, $q$ jest drugą współrzędną wierzchołka paraboli, funkcja ma jedno miejsce zerowe $x_{0}$ , to:

funkcja przyjmuje tylko wartości ujemne należące do przedziału $(- \infty, 0)$ dla $x \in (- \infty, x_{0}) \cup (x_{0}, \infty)$ .

R11LRmuHl1bjT

V. Jeżeli ramiona paraboli, która jest wykresem funkcji kwadratowej, są skierowane do góry, $q$ jest drugą współrzędną wierzchołka paraboli, funkcja nie ma miejsc zerowych, to:

,funkcja przyjmuje wartości dodatnie należące do przedziału $⟨q, \infty)$ dla $x \in ℝ,$
funkcja nie przyjmuje wartości ujemnych..

RgWMr5ZgXl49A

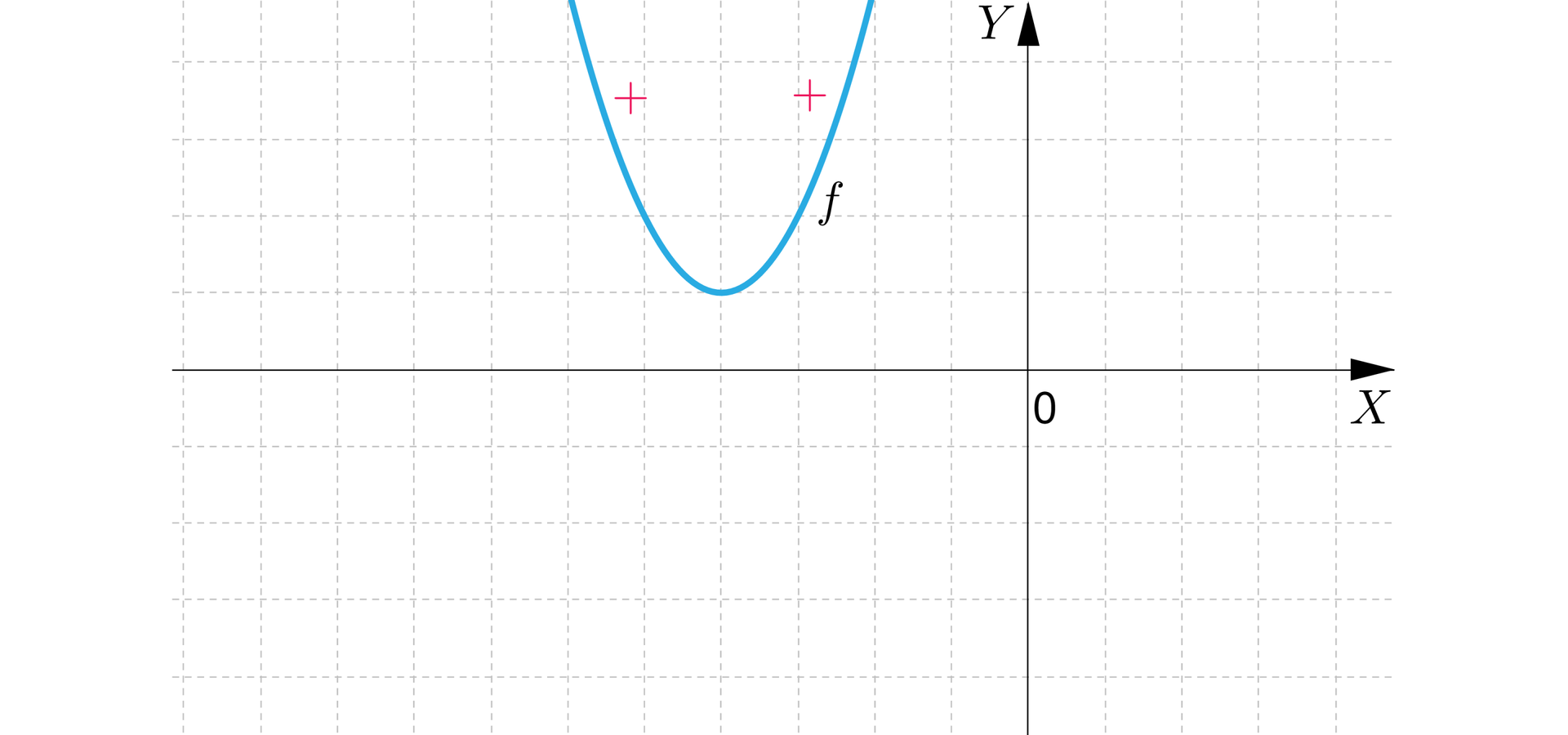
VI. Jeżeli ramiona paraboli, która jest wykresem funkcji kwadratowej, są skierowane do dołu, $q$ jest drugą współrzędną wierzchołka paraboli, funkcja nie ma miejsc zerowych, to:

wartości ujemne funkcji znajdują się w przedziale $(- \infty, q⟩$ dla $x \in ℝ,$
funkcja nie przyjmuje wartości dodatnich.

R1OghYbfczMPh

Przykład 1

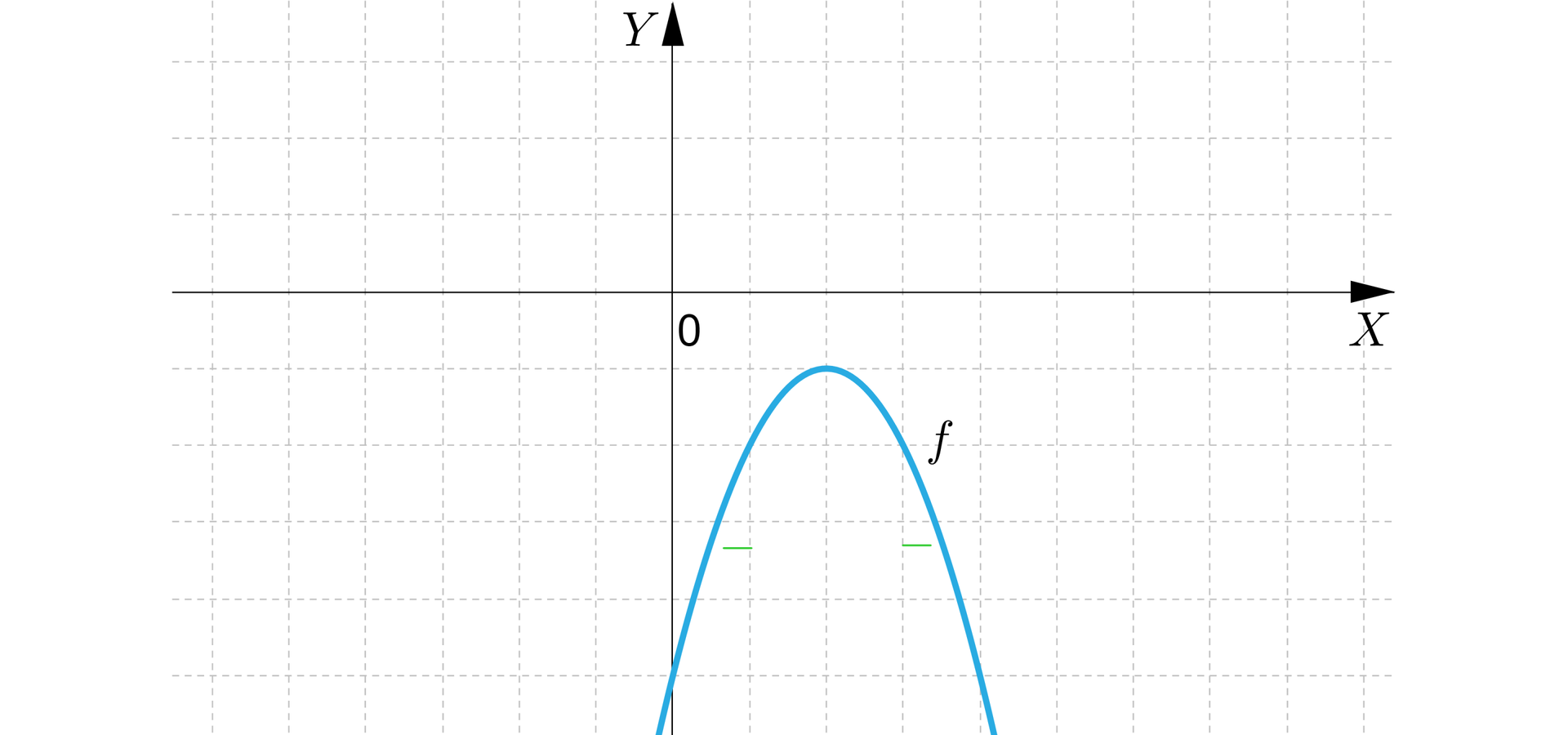
Określimy, dla jakich argumentów funkcja $f$ , której wykres przedstawiono na poniższym rysunku, przyjmuje wartości dodatnie, a dla jakich ujemne.

RZPlPBghG9iBy

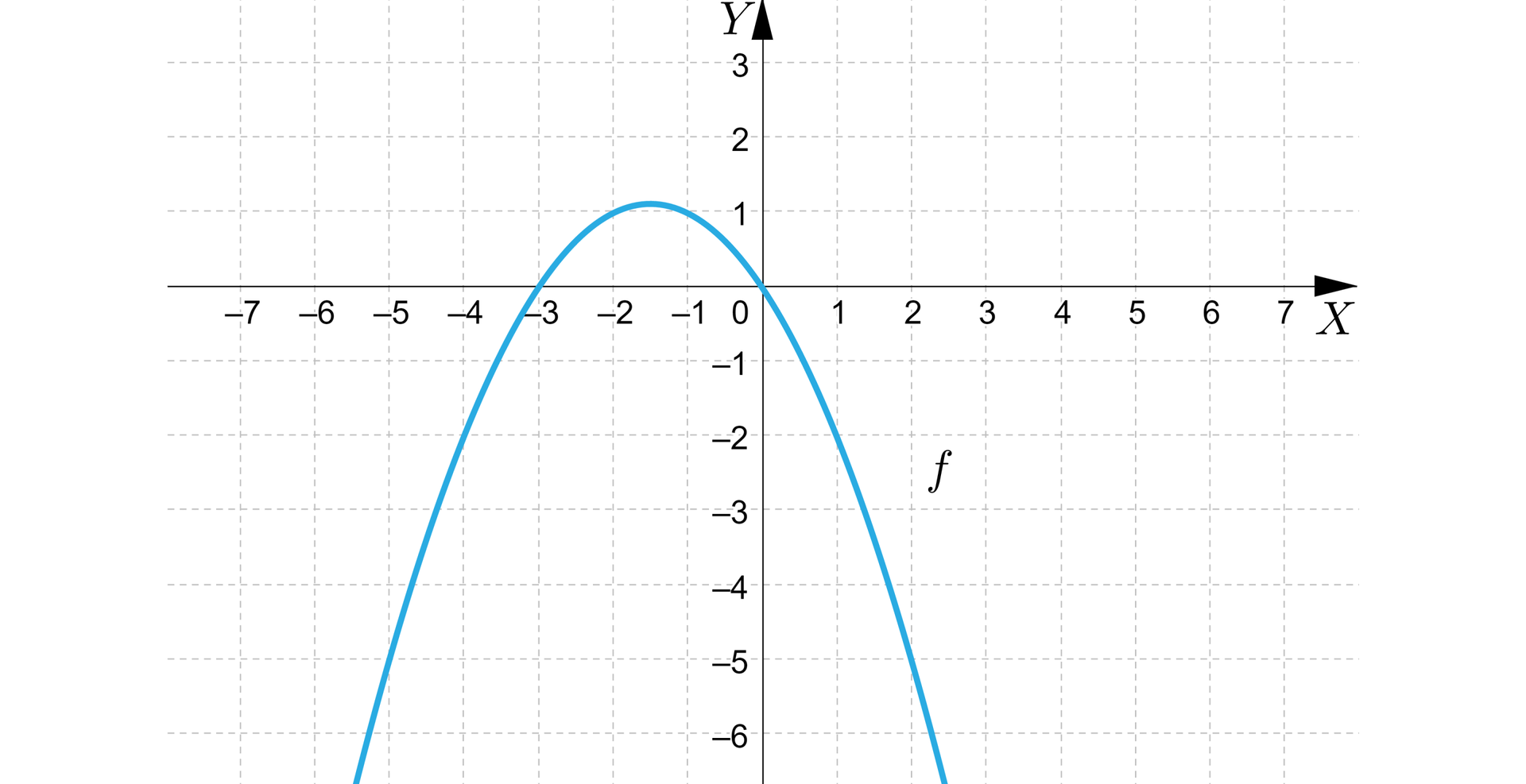
Ilustracja przedstawia poziomą oś X od minus siedmiu do siedmiu i pionowa oś Y od minus sześciu do trzech. Na rysunku zaznaczono także wykres funkcji kwadratowej będącą parabolą z ramionami skierowanymi w dół i z wierzchołkiem w punkcie nawias minus jeden przecinek pięć średnik jeden koniec nawiasu. Wykres funkcji posiada dwa miejsca zerowe, pierwsze w punkcie nawias minus trzy średnik zero koniec nawiasu oraz drugie w punkcie nawias zero średnik zero koniec nawiasu.

Rozwiązanie:

Funkcja $f$ przyjmuje wartości:

dodatnie dla argumentów należących do przedziału $(- 3, 0)$ ,
ujemne dla argumentów należących do przedziału $(- \infty, - 3) \cup (0, \infty)$ .

Rij4JlhbYemQi

Ilustracja przedstawia poziomą oś X od minus siedmiu do siedmiu i pionowa oś Y od minus trzech do sześciu. Na rysunku zaznaczono także wykres funkcji kwadratowej będącą parabolą z ramionami skierowanymi do góry i z wierzchołkiem w punkcie nawias dwa średnik minus jeden przecinek trzy koniec nawiasu. Wykres funkcji posiada dwa miejsca zerowe, pierwsze w punkcie nawias zero średnik zero koniec nawiasu oraz drugie w punkcie nawias cztery średnik zero koniec nawiasu.

Rozwiązanie:

Funkcja $f$ przyjmuje wartości:

dodatnie dla argumentów należących do przedziału $(- \infty, 0) \cup (4, \infty)$ ,
ujemne dla argumentów należących do przedziału $(0, 4)$ .

Jeżeli funkcja kwadratowa jest określona za pomocą pewnego wzoru, wówczas możemy wyznaczyć jej miejsca zerowe (o ile istnieją) i określić argumenty, dla których funkcja przyjmuje wartości dodatnie oraz ujemne.

Przykład 2

Wyznaczymy, dla jakich argumentów funkcja kwadratowa $f$ określona wzorem $f (x) = - x^{2} + 2 x$ przyjmuje wartości dodatnie, a dla jakich wartości ujemne.

Rozwiązanie:

Wzór funkcji $f$ możemy zapisać w postaci:

$f (x) = - x (x - 2)$ .

Miejscami zerowymi funkcji $f$ są liczby $0$ i $2$ .

Ponieważ $a = - 1 < 0$ , zatem ramiona paraboli, która jest wykresem tej funkcji, są skierowane do dołu.

Wobec tego funkcja $f$ przyjmuje wartości:

ujemne dla $x \in (- \infty, 0) \cup (2, \infty)$ ,
dodatnie dla $x \in (0, 2)$ .

Przykład 3

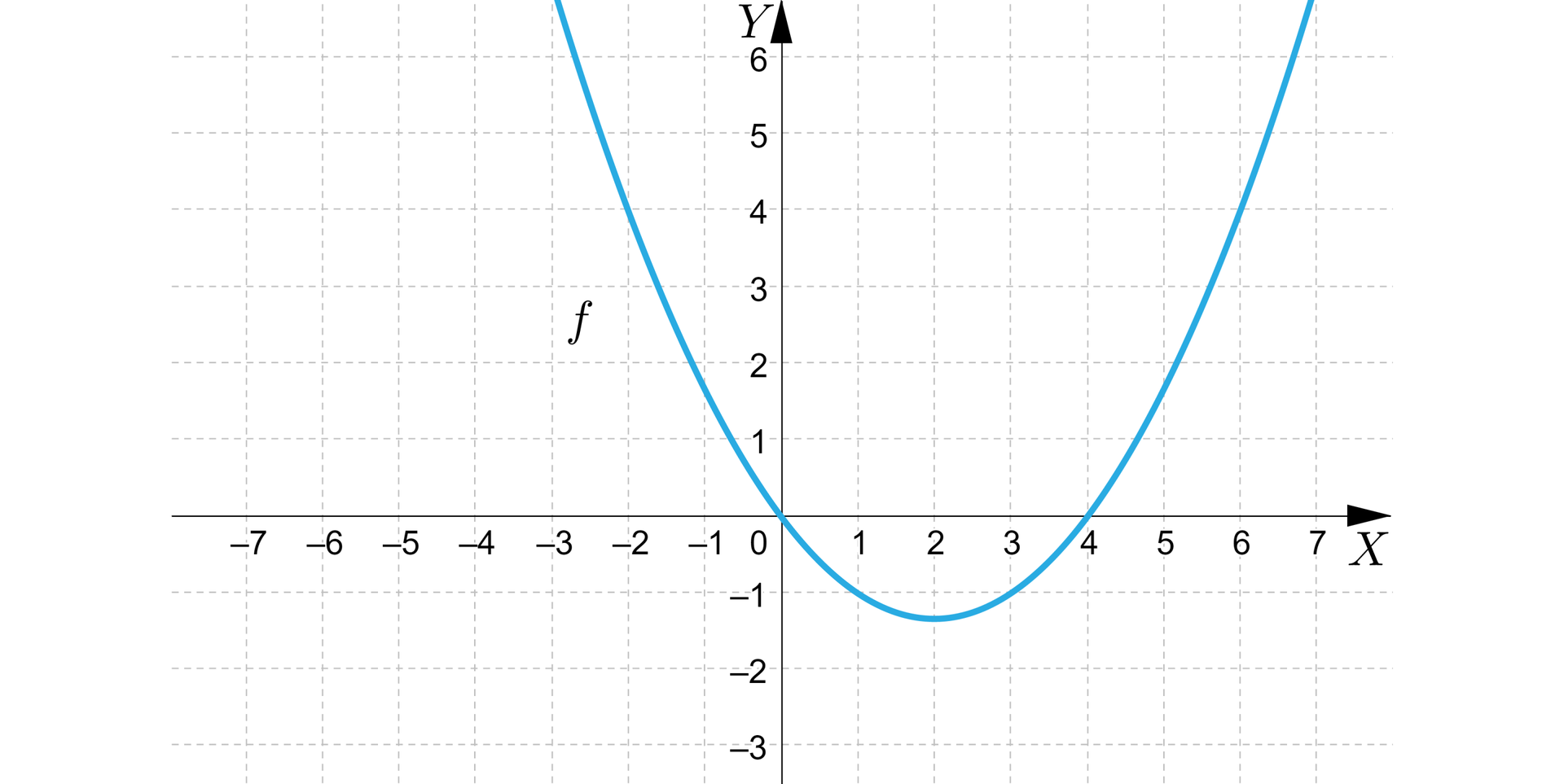
Na podstawie wykresu odczytamy wartości ujemne oraz dodatnie funkcji kwadratowej $f$ oraz określimy argumenty, dla których te wartości są przyjmowane.

R1AC40Ax4HU1e

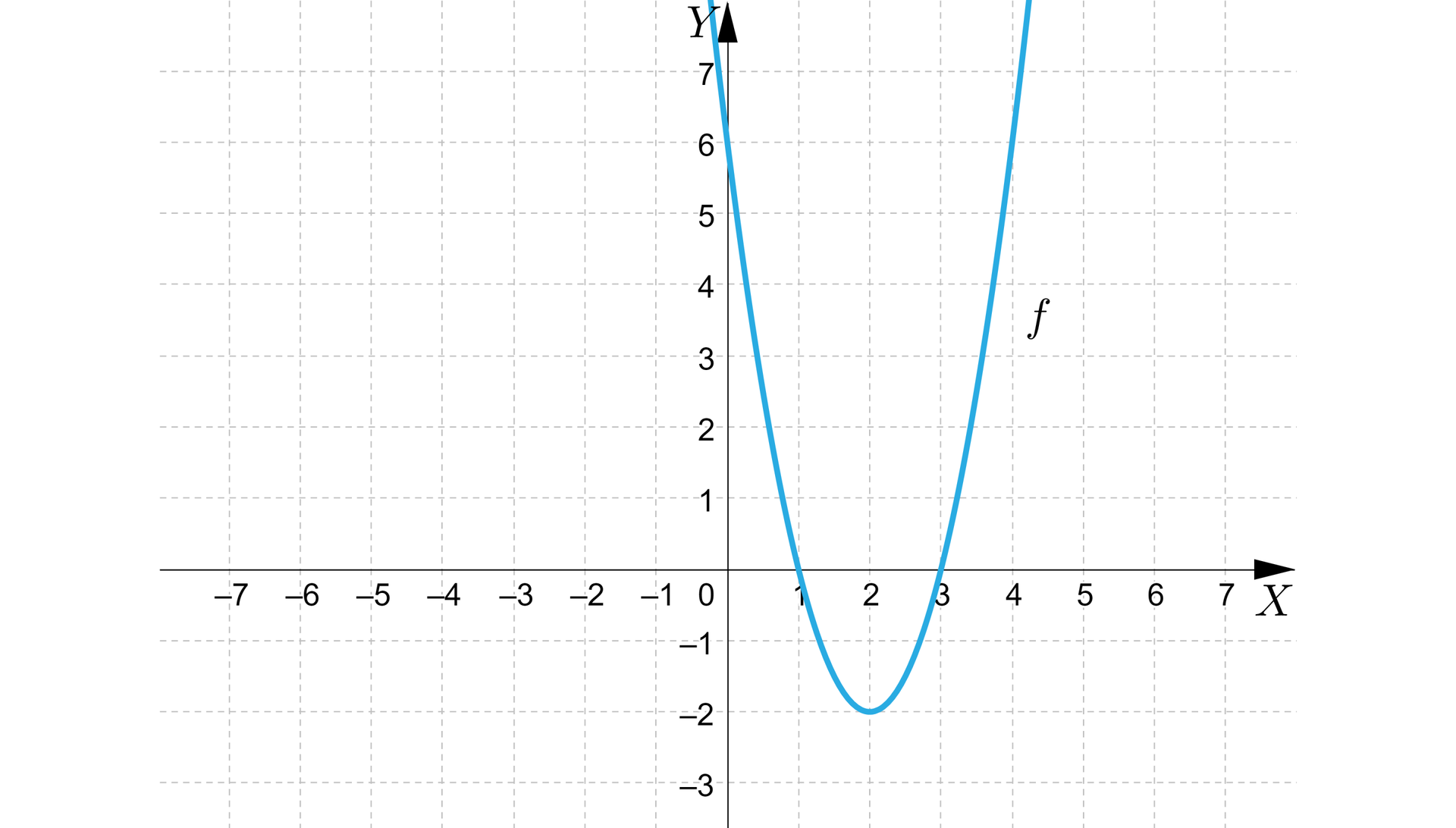
Rozwiązanie:

Z wykresu odczytujemy, że:

funkcja $f$ przyjmuje wartości ujemne należace do przedziału $⟨- 2, 0)$ dla argumentów $x \in (1, 3)$ ,
funkcja $f$ przyjmuje wartości dodatnie należące do przedziału $(0, \infty)$ dla argumentów $x \in (- \infty, 1) \cup (3, \infty)$ .

Umiejętność odczytywania argumentów, dla których funkcja kwadratowa przyjmuje wartości ujemne lub dodatnie, pozwala na rozwiązywanie nierówności kwadratowych typu $f (x) > 0$ lub $f (x) < 0$ .

Przykład 4

Dana jest funkcja kwadratowa $f$ . Wyznaczymy rozwiązania nierówności $f (x) > 0$ oraz $f (x) < 0$ .

a) $f (x) = - 3 x^{2}$

b) $f (x) = x^{2} - 5 x + 6$

Rozwiązanie:

a) Miejscem zerowym funkcji $f$ jest liczba $0$ a ramiona paraboli, która jest wykresem tej funkcji, są skierowane do dołu.

Zatem:

$f (x) > 0$ dla $x \in \emptyset$ ,
$f (x) < 0$ dla $x \in ℝ ∖ \{0\}$ .

b) Miejscami zerowymi funkcji $f$ są liczby $2$ i $3$ a ramiona paraboli, która jest wykresem tej funkcji, są skierowane do góry.

Zatem:

$f (x) < 0$ dla $x \in (2, 3)$ ,
$f (x) > 0$ dla $x \in (- \infty, 2) \cup (3, \infty)$ .

Przykład 5

Określimy, dla jakich argumentów funkcja kwadratowa $f$ określona wzorem $f (x) = x^{2} - 4 |x|$ przyjmuje wartości niedodatnie.

Rozwiązanie:

Zauważmy, że:

$f (x) = x^{2} - 4 |x| = {\begin{cases} x^{2} - 4 x, d l a x \geq 0 \\ x^{2} + 4 x, d l a x < 0 \end{cases}$

Funkcja $f$ ma trzy miejsca zerowe: $(- 4)$ , $0$ , $4$ .

Wykres funkcji $f$ przedstawia się następująco:

R1cRPWy6TYssI

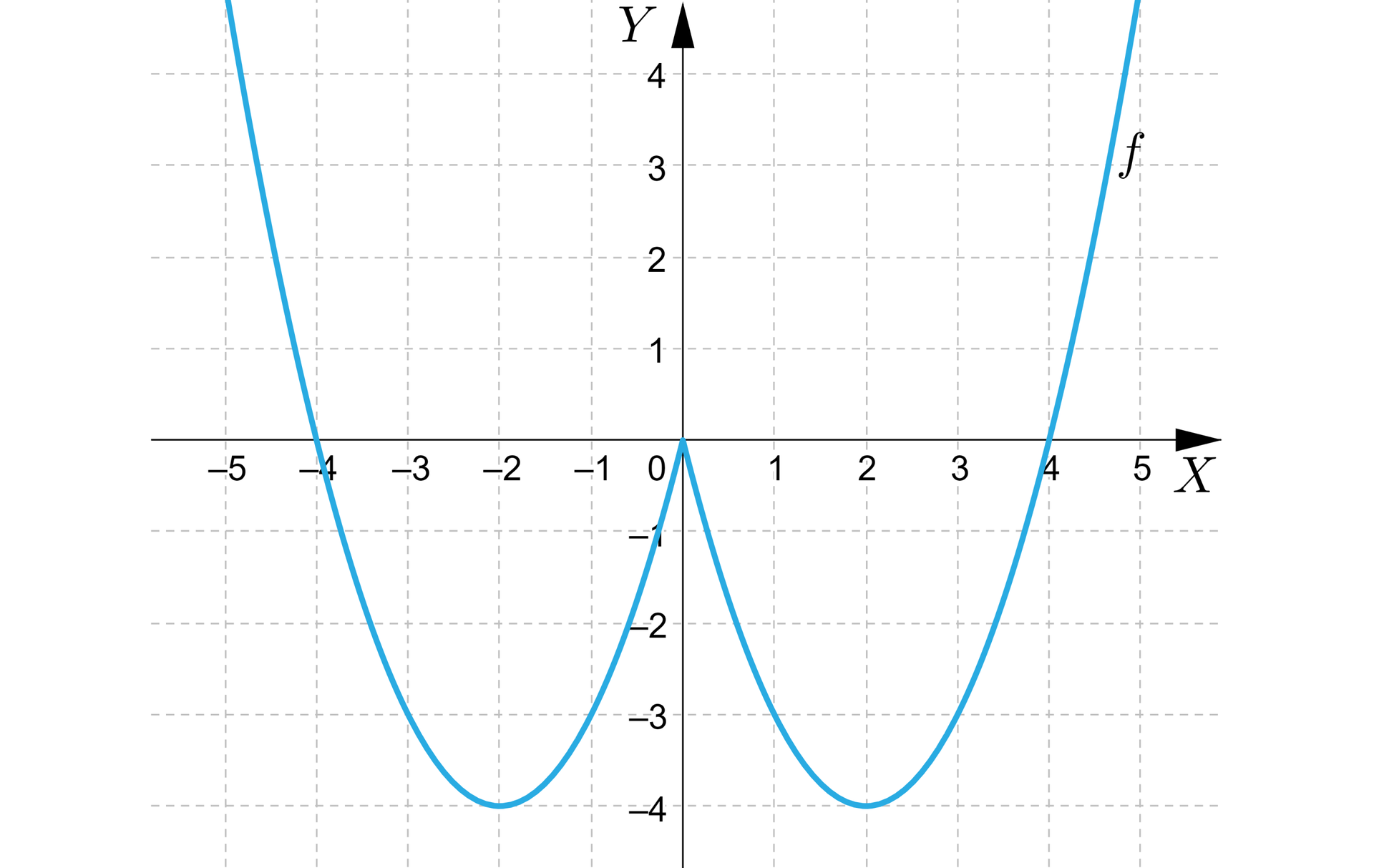
Ilustracja przedstawia poziomą oś X od minus siedmiu do siedmiu i pionowa oś Y od minus trzech do sześciu. Na rysunku zaznaczono także wykres dwóch funkcji kwadratowych będącymi parabolami obie z ramionami skierowanymi do góry. Pierwsza z nich posiada wierzchołek w punkcie nawias minus dwa średnik minus cztery koniec nawiasu. Wykres funkcji posiada dwa miejsca zerowe, pierwsze w punkcie nawias minus cztery średnik zero koniec nawiasu oraz drugie w punkcie nawias zero średnik zero koniec nawiasu. Druga parabola posiada wierzchołek w punkcie nawias dwa średnik minus cztery koniec nawiasu i także ma dwa miejsca zerowe, pierwsze w punkcie nawias zero średnik zero koniec nawiasu oraz drugie w punkcie nawias cztery średnik zero koniec nawiasu. Obie funkcje łączą się w punkcie nawias zero średnik zero koniec nawiasu.

Z wykresu odczytujemy, że:

$f (x) \leq 0$ dla $x \in ⟨- 4, 4⟩$ .

Przykład 6

Wyznaczymy dziedzinę funkcji $f$ określonej wzorem $f (x) = \sqrt{- x^{2} + 16}$ .

Rozwiązanie:

Rozpatrzmy pomocniczo funkcję $g$ określoną wzorem $g (x) = - x^{2} + 16$ .

Zauważmy, że do wyznaczenia dziedziny funkcji $f$ wystarczy określić, dla jakich argumentów funkcja $g$ przyjmuje wartości nieujemne.

Wzór funkcji $g$ zapisujemy w postaci:

$g (x) = - x^{2} + 16 = (4 + x) \cdot (4 - x)$ .

Miejscami zerowymi funkcji $g$ są liczby $(- 4)$ oraz $4$ .

Ponieważ $a = - 1 < 0$ , zatem ramiona paraboli, która jest wykresem funkcji $g$ są skierowane do dołu.

Wobec tego funkcja $g$ przyjmuje wartości nieujemne dla $x \in ⟨- 4, 4⟩$ .

Zatem otrzymany przedział jest dziedziną funkcji $f$ .

Słownik

funkcja kwadratowa

funkcja określona na zbiorze $ℝ$ wzorem

f (x) = a x^{2} + b x + c

gdzie $a, b, c \in ℝ$ oraz $a \neq 0$

zbiór wartości funkcji

zbiór wszystkich tych liczb, które można otrzymać w wyniku obliczenia wartości funkcji dla wszystkich jej argumentów

Wprowadzenie

Schemat interaktywny

Słownik