Przeczytaj

Już wiesz

Jak przesuwać wykres funkcji $y = f (x)$ wzdłuż osi $X$ o $p$ jednostek ( $p > 0$ ). Wówczas w wyniku przesunięcia:
- w prawo otrzymamy wykres funkcji $y = f (x - p)$ ,
- w lewo otrzymamy wykres funkcji $y = f (x + p)$ .

Jak zmienia się argument we wzorze danej funkcji, gdy przesuwamy wykres w prawo, a jak, gdy przesuwamy w lewo, wzdłuż osi $X$ .

Przykład 1

Naszkicujemy wykres funkcji $g$ , stosując odpowiednie przesunięcie wykresu funkcji $f (x) = |x|$ . Podamy miejsca zerowemiejsce zerowe funkcjimiejsca zerowe funkcji $g$ .

a) $g (x) = |x - 3|$

Wiemy już, że wzór funkcji $y = f (x - 3)$ oznacza przesunięcie w prawoprzesunięcie w prawoprzesunięcie w prawo o $3$ jednostki, wzdłuż osi $X$ wykresu funkcji $y = f (x)$ .

Rozpoczynamy od sporządzenia wykresu funkcji $f (x) = |x|$ , a następnie przesuwamy go (zgodnie z wcześniejszym ustaleniem) o $3$ jednostki w prawo, otrzymując wykres funkcji $g (x) = |x - 3|$ .

RDQbunkhTGQgK2

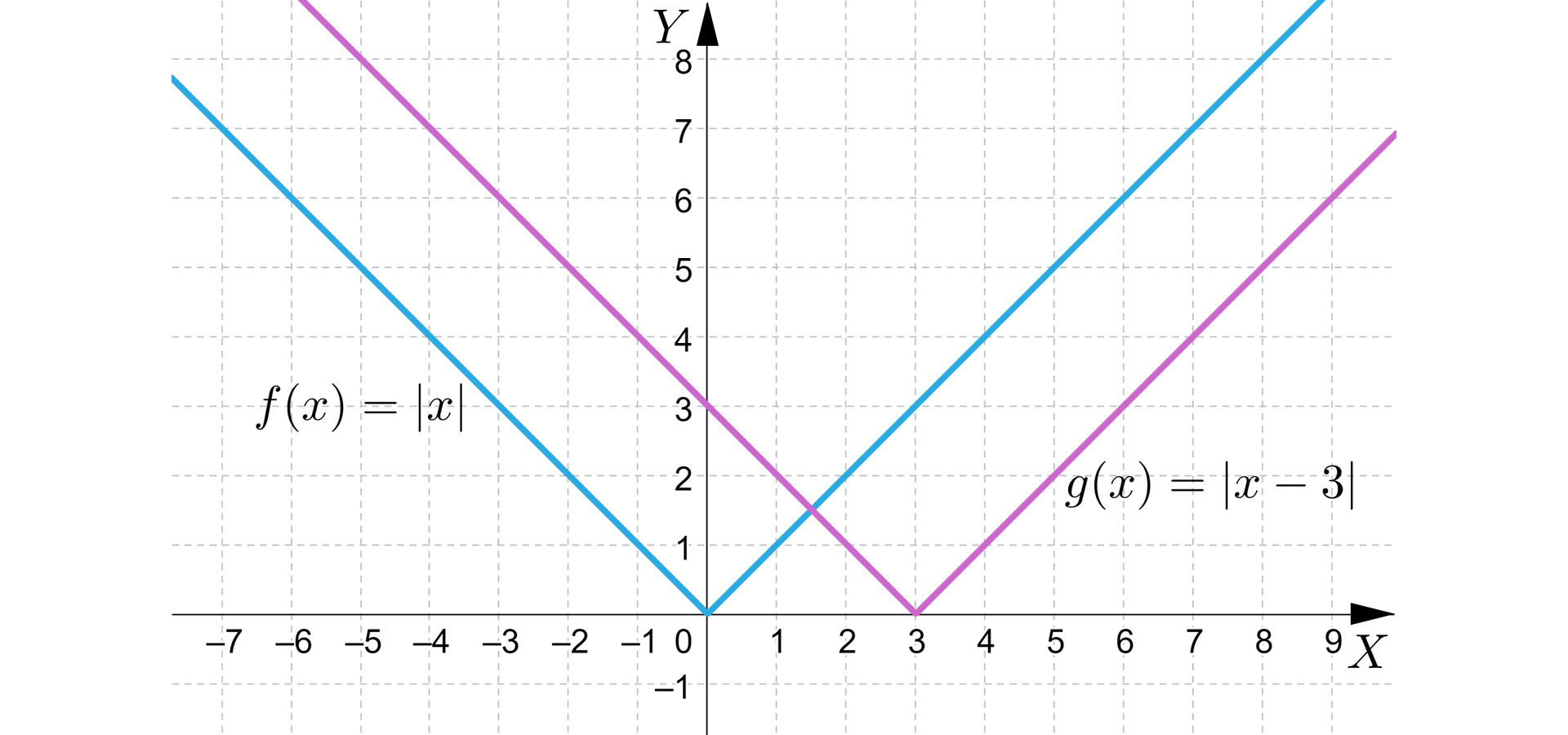
Na rysunku przedstawiony jest układ współrzędnych z poziomą osią X od minus jedenastu do pięciu oraz z pionową osią Y od minus jeden do ośmiu. W układzie zaznaczono dwa wykresy funckji w postaci łamanych. Pierwszy wykres funckji maleje do początku układu współrzędnych przechodząc przez punkty -2,2 oraz -1,1 a następnie rośnie przechodząc przez punkty o współrzędnych 1,1 i 2,2. Wykres funckji opisany jest wzorem fx=x. Drugi wykres funckji maleje do punktu 3,0 przechodząc przez punkty -2,5 oraz -1,4 a następnie rośnie przechodząc przez punkty o współrzędnych 5,2 i 6,3. Wykres funckji opisany jest wzorem fx=x-3.

Zwróćmy uwagę, że miejscem zerowym funkcji $f (x) = |x|$ jest $x = 0$ . Wykres funkcji $g (x) = |x - 3|$ otrzymaliśmy w wyniku przesunięcia wykresu funkcji $f$ o $3$ jednostki w prawo, więc i punkt wspólny wykresu i osi odciętych został przesunięty o $3$ jednostki w prawo. Zatem miejscem zerowym funkcji $g$ jest $x = 3$ .

b) $g (x) = |x + 5|$

Postępując analogicznie, jak w przykładzie a)- rozpoczynamy pracę od przypomnienia, że wzór $y = f (x + 5)$ oznacza przesunięcie w lewoprzesunięcie w lewoprzesunięcie w lewo o $5$ jednostek, wzdłuż osi $X$ wykresu funkcji $y = f (x)$ .

Sporządzamy wykres funkcji $f (x) = |x|$ , przesuwamy go o $5$ jednostek w lewo, wzdłuż osi $X$ .

RvHwtWzvNNS0b

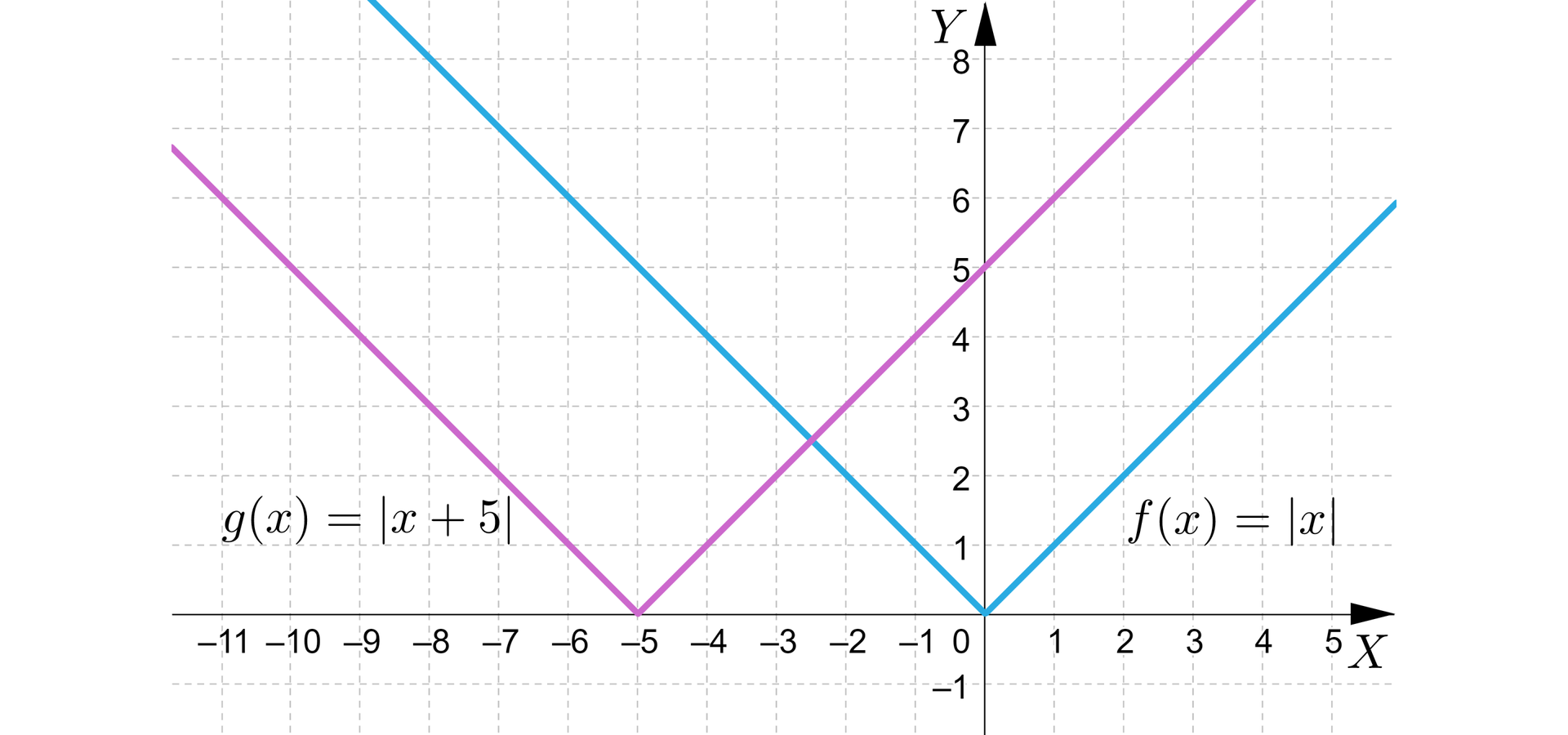
Miejscem zerowym funkcji $g$ jest $x = - 5$ , co ma swoje uzasadnienie w przesunięciu w lewo o $5$ jednostek odpowiedniego punktu wykresu funkcji $f$ .

Przykład 2

RJhGjWyw9KiTn2

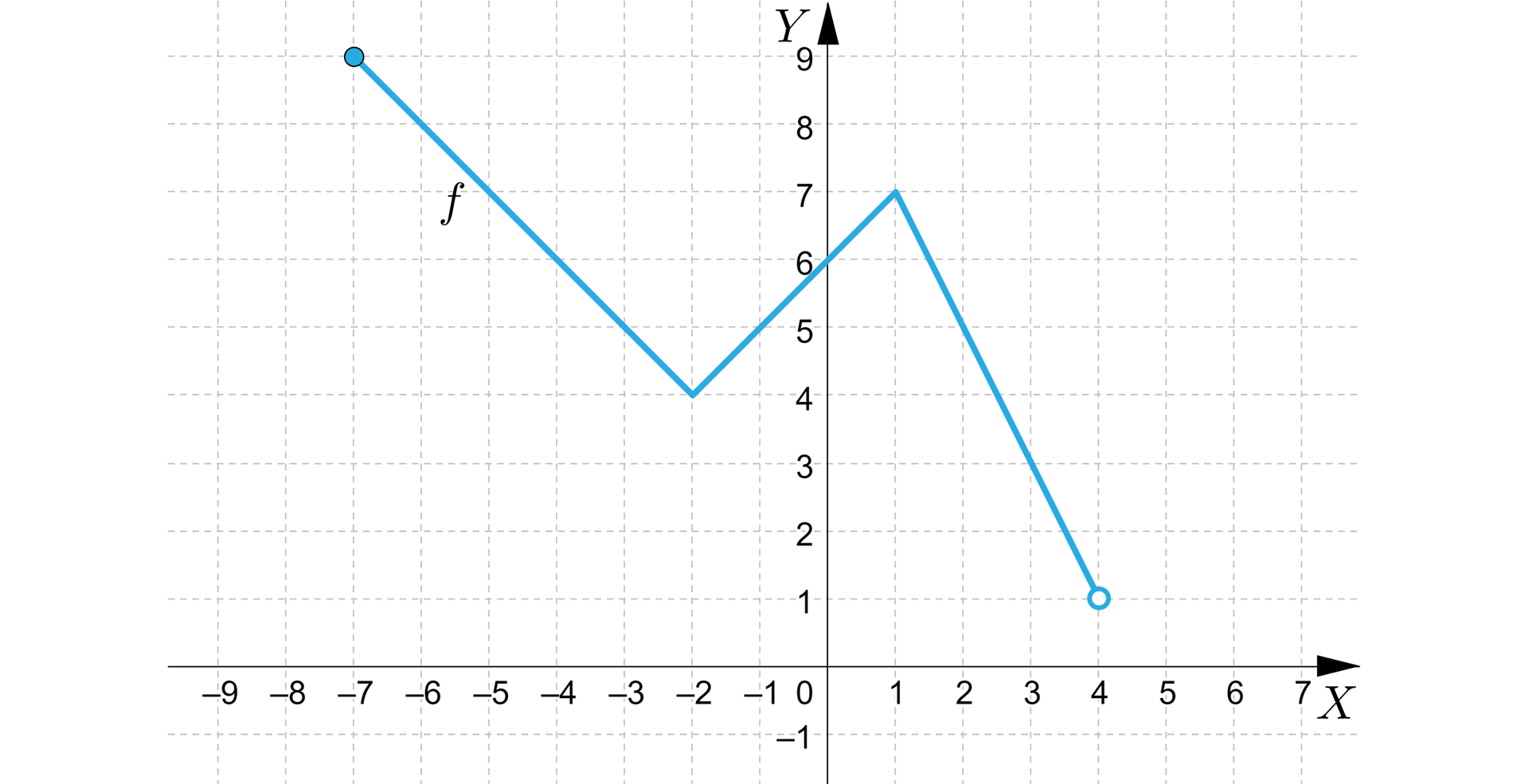
Na rysunku przedstawiony jest układ współrzędnych z poziomą osią X od minus dziewięciu do siedmiu oraz z pionową osią Y od minus jeden do dziewięciu. W układzie zaznaczono wykres funkcji w postaci łamanej, która zaczyna się w punkcie należącym do wykresu o współrzędnych -8,9. Następnie wykres funkcji maleje do punktu o współrzędnych -2,4, a potem rośnie do punktu o współrzędnych 1,7. Ostatecznie wykres funkcji maleje do punktu nie należącego do wykresu o współrzędnych 4,1.

Na powyższym rysunku przedstawiono wykres funkcji $f : ⟨- 7, 4) \to (1, 9⟩$ . Naszkicujemy wykres funkcji $g (x) = f (x - 4)$ i podamy jej dziedzinędziedzina funkcjidziedzinę oraz zbiór wartościzbiór wartości funkcjizbiór wartości.

Zaczynamy od interpretacji wzoru $g (x) = f (x - 4)$ , który oznacza przesunięcie w prawoprzesunięcie w prawo o $4$ jednostki, wzdłuż osi $X$ danego wykresu.

RMr6ctL8ST5FA

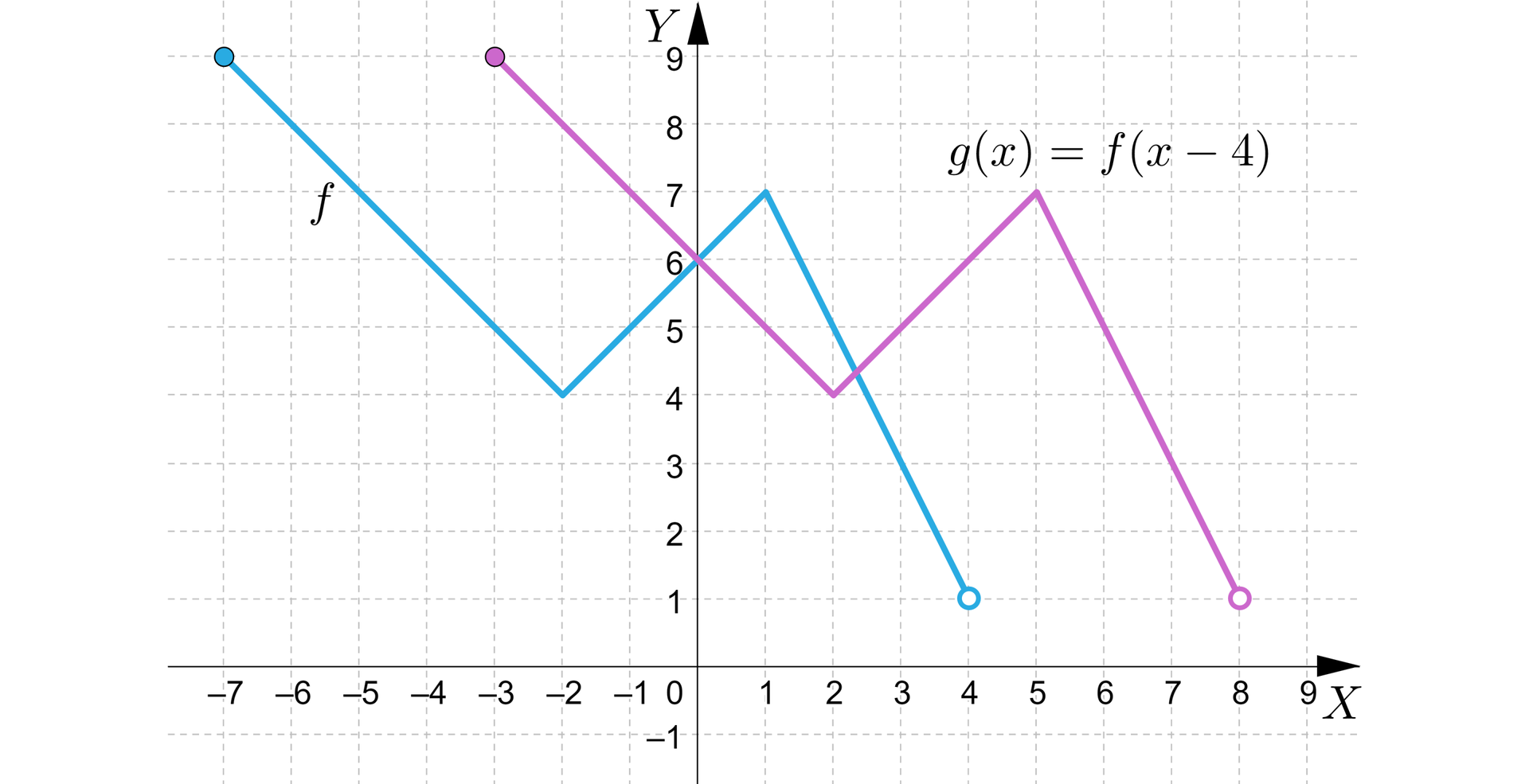
Z wykresu odczytamy dziedzinę oraz zbiór wartości funkcji $g$ .

$D_{g} = ⟨- 3, 8)$

$Z W_{g} = (1, 9⟩$

Przykład 3

Uzupełnimy tabelę, mając własności funkcji $f$ .

Funkcja	Dziedzina	Miejsca zerowe
$f (x)$	$D_{f} = ⟨- 5, 2⟩ \cup \{4, 5, 6\}$	$- 3, 1, 5$
$g (x) = f (x + 7)$
$g (x) = f (x - 6)$

Rozwiązanie rozpoczynamy od wyjaśnienia wzoru $g (x) = f (x + 7)$ . Wiemy już, że oznacza on przesunięcie w lewoprzesunięcie w lewoprzesunięcie w lewo o $7$ jednostek wykresu danej funkcji, co ma przełożenie na przesunięcie o $7$ jednostek w lewo każdego punktu wykresu.

Zatem: $D_{g} = ⟨- 12, - 5⟩ \cup \{- 3, - 2, - 1\}$ , zaś miejscami zerowymi tej funkcji są liczby: $- 10$ , $- 6$ , $- 2$ .

Podobnie postępujemy w przypadku funkcji $g (x) = f (x - 6)$ . Wzór ten oznacza, że wykres danej funkcji należy przesunąć w prawoprzesunięcie w prawoprzesunąć w prawo o $6$ jednostek, czyli każdemu argumentowi funkcji, odpowiada liczba o 5 większa. Z powyższego wynika, że $D_{g} = ⟨1, 8⟩ \cup \{10, 11, 12\}$ , miejscami zerowymi funkcji są liczby: $3$ , $7$ , $11$ .

Funkcja	Dziedzina	Miejsca zerowe
$f (x)$	$D_{f} = ⟨- 5, 2⟩ \cup \{4, 5, 6\}$	$- 3, 1, 5$
$g (x) = f (x + 7)$	$D g = ⟨- 12, - 5⟩ \cup \{- 3, - 2, - 1\}$	$- 10, - 6, - 2$
$g (x) = f (x - 6)$	$D_{g} = ⟨1, 8⟩ \cup \{10, 11, 12\}$	$3, 7, 11$

Przykład 4

Dany jest wykres funkcji $f$ .

RZKtzPCFWrZo12

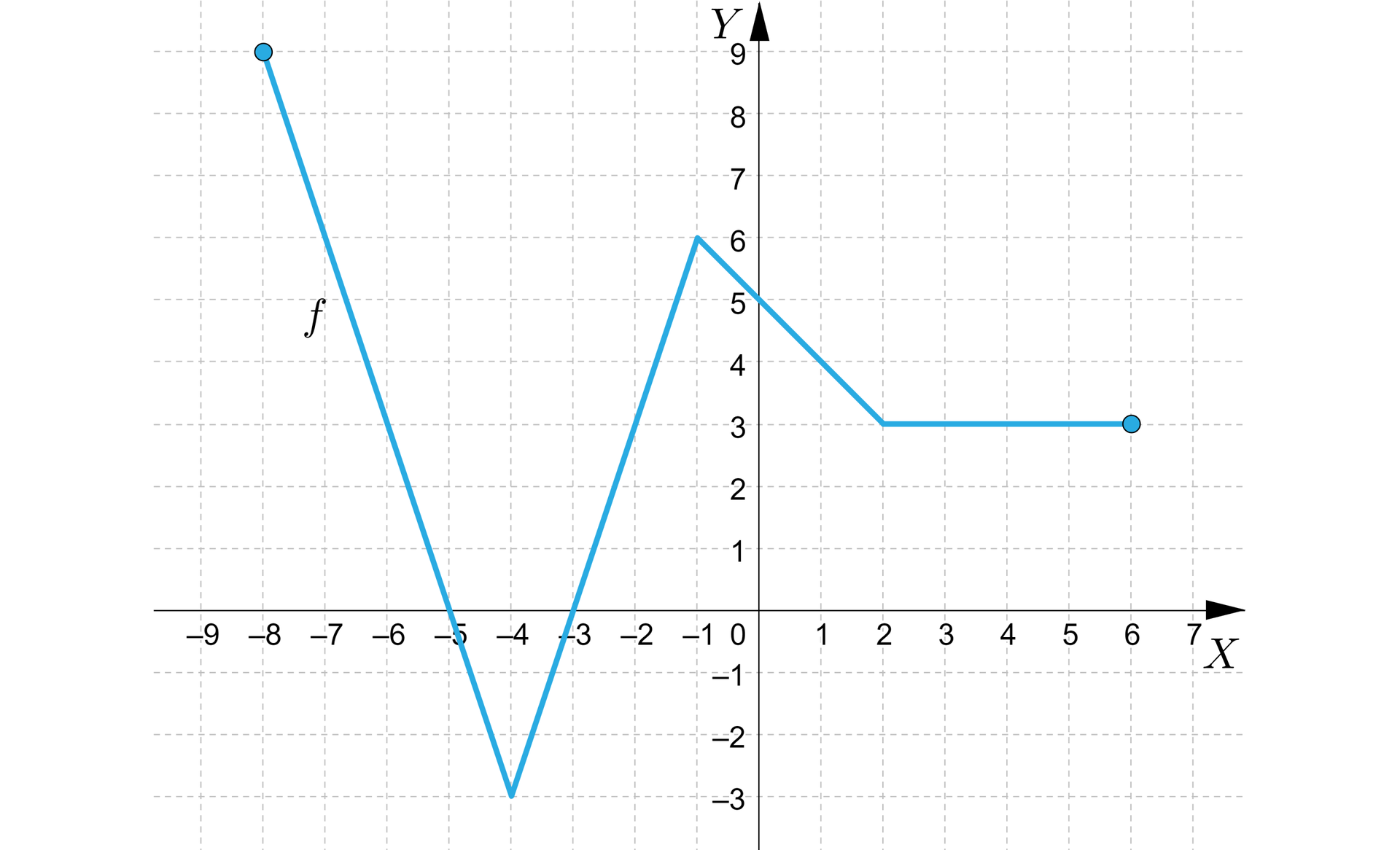
Na rysunku przedstawiony jest układ współrzędnych z poziomą osią X od minus dziewięciu do siedmiu oraz z pionową osią Y od minus trzech do dziewięciu. Wykres funkcji jest w postaci łamanej, który zaczyna się w punkcie należącym do wykresu funkcji o współrzędnych -8,9. Następnie wykres funkcji maleje do punktu o współrzędnych -4,-3 a potem rośnie do punktu (-1,6). Dalej wykres funkcji maleje do punktu (2,3) i ostatecznie od podanego punktu wykres funkcji jest stały do punktu o współrzędnych (6,3) , który należy do wykresu funkcji.

Wyznaczymy dziedzinędziedzina funkcjidziedzinę, zbiór wartościzbiór wartości funkcjizbiór wartości, miejsca zerowemiejsce zerowe funkcjimiejsca zerowe, maksymalne przedziały monotoniczności danej funkcji oraz funkcji:

a) $g (x) = f (x - 1)$

b) $g (x) = f (x + 2)$

Rozwiązanie rozpoczniemy od wypisania wszystkich informacji na temat funkcji $f$

$D_{f} = ⟨- 8, 6⟩$
$Z W_{f} = ⟨- 3, 9⟩$
miejsca zerowe funkcji $f$ : $- 5$ , $- 3$
maksymalne przedziały monotoniczności:
funkcja maleje w przedziałach $⟨- 8, - 4⟩, ⟨- 1, 2⟩$
funkcja rośnie w przedziale $⟨- 4, - 1⟩$
funkcja jest stała w przedziale $⟨2, 6⟩$ .

RqP3Agoyk9xxo

ad.a) Wyznaczymy własności funkcji

g (x) = f (x - 1)

, pamiętając o tym, że wzór ten oznacza przesunięcie w prawo danego wykresu funkcji

D_{g} = <mfenced open="<" close=">"> - 7, 7

miejscami zerowymi funkcji

g

są liczby:

4

2

maksymalne przedziały monotoniczności funkcji

g

funkcja maleje w przedziałach:

<mfenced open="<" close=">"> - 7, - 3, <mfenced open="<" close=">"> 0, 3

funkcja rośnie w przedziale

<mfenced open="<" close=">"> - 3, 0

funkcja jest stała w przedziale

<mfenced open="<" close=">"> 3, 6

ad a)
Wyznaczymy własności funkcji $g (x) = f (x - 1)$ , pamiętając o tym, że wzór ten oznacza przesunięcie w prawo o $1$ jednostkę danego wykresu funkcji

D_{g} = "⟨"- 7, 7"⟩"

Z W_{g} = "⟨"- 3, 9"⟩"

miejscami zerowymi funkcji

g

są liczby:

- 4

- 2

maksymalne przedziały monotoniczności funkcji

g

funkcja maleje w przedziałach:

"⟨"- 7, - 3"⟩", "⟨"0, 3"⟩"

funkcja rośnie w przedziale

"⟨"- 3, 0"⟩"

funkcja jest stała w przedziale

"⟨"3, 7"⟩"

ad b)
Wyznaczymy własności funkcji $g (x) = f (x + 2)$ , pamiętając o tym, że wzór ten oznacza przesunięcie w lewo o $2$ jednostki danego wykresu funkcji

D_{g} = "⟨"- 10, 4"⟩"

Z W_{g} = "⟨"- 3, 9"⟩"

miejscami zerowymi funkcji

g

są liczby:

- 7

- 5

maksymalne przedziały monotoniczności funkcji

g

funkcja maleje w przedziałach:

"⟨"- 10, - 6"⟩", "⟨"- 3, 0"⟩"

funkcja rośnie w przedziale

"⟨"- 6, - 3"⟩"

funkcja jest stała w przedziale

"⟨"0, 4"⟩"

Przykład 5

Dany jest wykres funkcji $f$ .

R3QqUCYEoykCd2

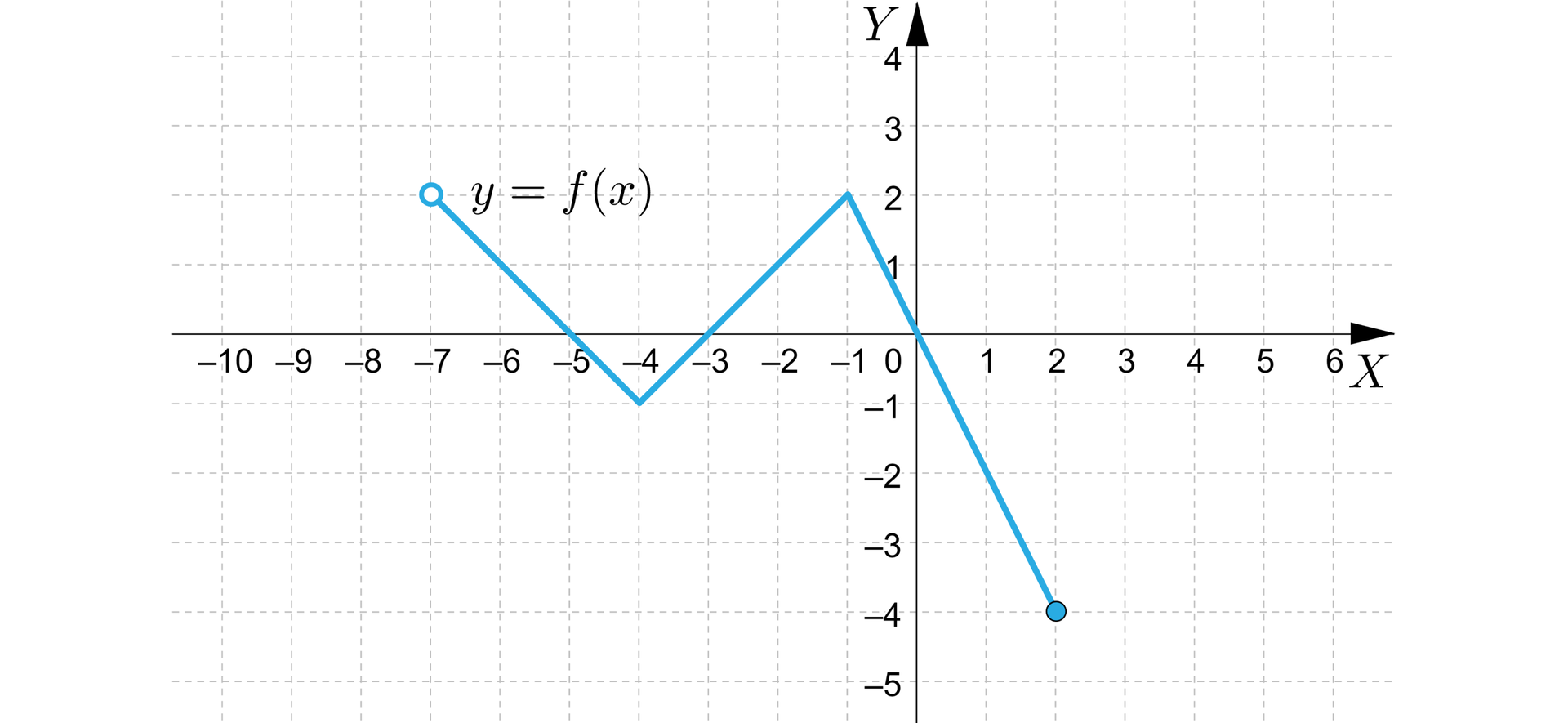
Na rysunku przedstawiony jest układ współrzędnych z poziomą osią X od minus dziesięciu do sześciu oraz z pionową osią Y od minus pięciu do dwóch. Wykres funkcji jest w postaci łamanej, który zaczyna sie w punkcie nie należącym do wykresu funkcji o współrzędnych -7,2. Następnie wykres funkcji maleje do punktu o współrzędnych -4,-1 a potem rośnie do punktu (-1,2). Dalej wykres funkcji maleje do punktu o współrzędnych (2,-4)</math, który należy do wykresu funkcji.

Wyznaczymy argumenty, dla których:

a) $f (x + 3) \geq 0$ ,

b) $f (x - 4) < 0$ .

ad a) Na początku ustalimy argumenty, dla których $f (x) \geq 0$ .

$f (x) \geq 0 \Leftrightarrow x \in (- 7, - 5⟩ \cup ⟨- 3, 0⟩$

$f (x + 3)$ oznacza przesunięcie w lewoprzesunięcie w lewoprzesunięcie w lewo o $3$ jednostki odpowiedniego wykresu, zatem

$f (x + 3) \geq 0 \Leftrightarrow x \in (- 10, - 8⟩ \cup ⟨- 6, - 3⟩$

ad b) Podobnie jak w przykładzie a), ustalamy argumenty dla których $f (x) < 0$ .

$f (x) < 0 \Leftrightarrow x \in (- 5, - 3) \cup (0, 2⟩$

$f (x - 4)$ oznacza przesunięcie w prawoprzesunięcie w prawoprzesunięcie w prawo o $4$ jednostki wykresu funcji f, zatem

$f (x - 4) < 0 \Leftrightarrow x \in (- 1, 1) \cup (4, 6⟩$ .

Ważne!

Przesunięcie wykresu funkcji $y = f (x)$ wzdłuż osi $X$ nie ma wpływu na:

zbiór wartości funkcji,
najmniejszą, największą wartość funkcji (o ile istnieją).

Słownik

przesunięcie w prawo

wzór $y = f (x - p)$ , gdzie $p > 0$ określa przesunięcie wykresu funkcji $y = f (x)$ w prawo o $p$ jednostek, wzdłuż osi $X$

przesunięcie w lewo

wzór $y = f (x + p)$ , gdzie $p > 0$ określa przesunięcie wykresu funkcji $y = f (x)$ w lewo o $p$ jednostek, wzdłuż osi $X$

dziedzina funkcji

dziedzina funkcji liczbowej określonej za pomocą wzoru - zbiór wszystkich liczb, dla których wzór funkcji ma sens liczbowy; z wykresu dziedzinę funkcji odczytujemy na osi $X$

zbiór wartości funkcji

zbiór wartości funkcji liczbowej - zbiór wszystkich tych liczb, które można otrzymać w wyniku obliczenia wartości funkcji dla wszystkich jej argumentów; z wykresu funkcji zbiór wartości odczytujemy na osi $Y$

miejsce zerowe funkcji

argument dla którego funkcja przyjmuje wartość $0$ ; mając wykres funkcji odczytujemy odciętą punktu przecięcia wykresu funkcji z osią $X$

Wprowadzenie

Symulacja interaktywna

Słownik