Przeczytaj
Diagram aktywności
Diagram przypadków użycia (omówiony w e‑materiale Programowanie obiektowe – projekt, etap IProgramowanie obiektowe – projekt, etap I) umożliwia odczytanie, co dany użytkownik może zrobić. Natomiast diagram aktywności pokazuje, jak można to osiągnąć.
Przeanalizujmy diagram obrazujący czynność wsiadania kierowcy do samochodu.

Diagram przedstawia kolejne kroki omawianej czynności. Zwróćmy uwagę, że:
czarna kropka oznacza początek aktywności (stosujemy tylko jedno takie oznaczenie),
strzałki wyznaczają następstwo akcji,
grot strzałki wskazuje kierunek, zgodnie z którym należy odczytywać diagram,
ramka z zaokrąglonymi rogami oznacza czynność lub akcję, którą należy w danym momencie wykonać,
akcja to pojedyncza, atomowa i niepodzielna operacja,
czynność to grupa zagregowanych akcji,
czarna kropka z pierścieniem oznacza koniec czynności.
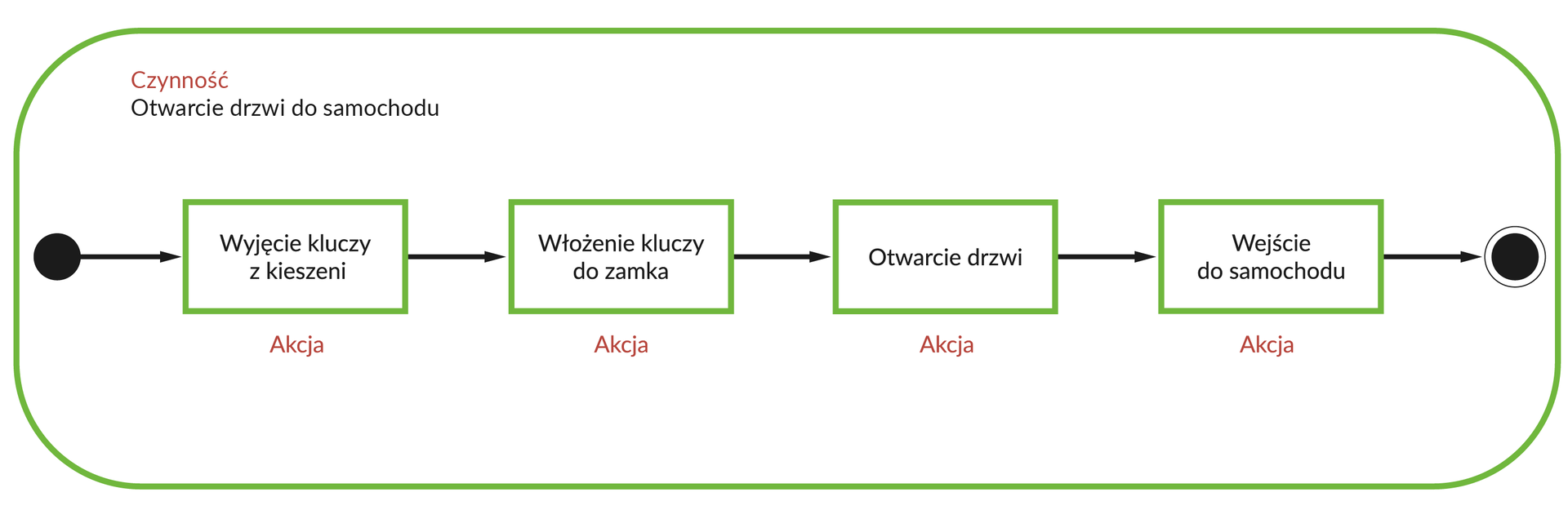
Czynność otwarcia drzwi składa się zatem z czterech, wykonywanych kolejno pojedynczych akcji.
W diagramie aktywności możemy stosować również bloczek rozgałęzienia, który ma postać deltoidu:

Bloczek ten pozwala sterować przebiegiem aktywności w zależności od stanu systemu. Domyślnie ma dwa wyjścia i zachowuje się podobnie jak operator warunkowy if‑else. Obydwa wyjścia oznaczają sytuacje przeciwne, jak w przedstawionym przykładzie – zamek w drzwiach może być albo otwarty, albo zamknięty i domyślnie nie ma trzeciego możliwego rozwiązania. Jeżeli jest zamknięty, przechodzimy do akcji wyjęcia kluczy z kieszeni, a jeżeli otwarty, przechodzimy bezpośrednio do akcji otwarcia drzwi.
Diagram aktywności przypomina programowanie. Obrazuje czynności, jakie muszą wystąpić po kolei w danym systemie, abyśmy mogli otrzymać końcowy wynik, który będzie zgodny z naszymi oczekiwaniami.
Za pomocą deltoidu oznaczamy również złączenie. Na przedstawionym przykładzie widzimy rozgałęzienie z wyborem środka lokomocji. W pierwszym przypadku akcja to Jazda autobusem, w drugim – Jazda samochodem. Po zakończeniu każdej z tych akcji strzałki łączą się w bloku złączenia, co oznacza, że dalszy ciąg podróży do szkoły będzie przebiegać tak samo w obu przypadkach.

Należy doprecyzować, że bloczek złączenia inicjuje dalsze działanie za każdym razem, gdy dotrze do niego sterowanie, nie czekając na sterowanie ze wszystkich węzłówwęzłów. Nie można więc za jego pomocą budować zależności współbieżnych.
Współbieżność to sytuacja, gdy akcje lub czynności dzieją się jednocześnie.
Rozwidlenie (fork), podobnie jak scalenie (join), oznaczamy za pomocą długiej kreski.
Współbieżność nie definiuje nam kolejności wykonywania działań, a jedynie informuje, że dzieją się one w tym samym czasie. Ponieważ nie ma znaczenia, w jakiej kolejności zostaną wykonane, nie powinny być od siebie zależne. Przyjrzyjmy się temu na przykładzie innej sytuacji:

W przedstawionym przykładzie po rozpoczęciu czynności powstają dwa ciągi akcji. Pierwszy składa się z jednej akcji (Wyjęcie makaronu z szafki), a drugi z dwóch (Wstawienie wody oraz Posolenie wody). Oba mogą być wykonywane niezależnie i nawet jednocześnie, bo nieistotne jest, czy najpierw wyjmiemy z szafki makaron, czy wstawimy wodę na kuchenkę. Natomiast akcja wsypania makaronu do wody rozpocznie się dopiero wtedy, gdy wszystkie wcześniejsze akcje zostaną zakończone. Ważne jest jedynie, że odbywają się one w tym samym momencie.
W pierwszych komputerach procesy nie mogły być współbieżne, a akcje wykonywały się po kolei. We współczesnych procesorach czynności dzieją się – z punktu widzenia użytkownika – jednocześnie. Dzięki temu może działać więcej niż jeden program. W tym samym czasie możemy mieć uruchomioną grę, przeglądarkę, odtwarzacz muzyki oraz setki procesów, które rywalizują o zasoby naszego procesora. Jednowątkowe i jednordzeniowe procesory wykonują de facto jedną operację na raz. Oznacza to, że aby mogły jednocześnie działać różne programy, czas pracy procesora musi być dzielony pomiędzy nie. Każdy proces otrzymuje do dyspozycji określony czas, w jakim jest realizowany, po czym procesor zaczyna obsługę kolejnego procesu. Oczywiście im więcej uruchomionych procesów, tym większe obciążenie procesora, a co za tym idzie – wolniejsze wykonywanie programów. Procesory wielowątkowe i wielordzeniowe potrafią natomiast realizować wiele procesów w tym samym czasie, bez konieczności przełączania się pomiędzy nimi. Każdy proces realizowany jest w oddzielnym wątku. Obecnie najpopularniejsze są procesory dwu- i czterordzeniowe. Oznacza to, że procesor zbudowany jest z dwóch fizycznych rdzeni (mówiąc w dużym uproszczeniu: z dwóch oddzielnych procesorów, połączonych jednak w jeden układ). Dodatkowo każdy rdzeń, dzięki wykorzystaniu techniki wielowątkowości (ang. multithreading) potrafi obsługiwać jednocześnie wiele wątków. Dzięki temu np. procesor czterordzeniowy może realizować aż osiem wątków w tym samym czasie – ma więc ośmiokrotnie większą wydajność niż identyczny procesor jednordzeniowy z jednym wątkiem. Jeśli chcesz samodzielnie zgłębić temat budowy procesora, sięgnij do odpowiedniej literatury, np. Organizacja i architektura systemu komputerowego Williama Stallingsa.
W diagramie aktywności istnieje również możliwość przenoszenia obiektów pomiędzy czynnościami.

W diagramie wybraliśmy obiekt (Makaron), a następnie przekazaliśmy go do kolejnej czynności, jaką jest Ugotowanie makaronu. Zakładamy, że Wybór makaronu ma wpływ na końcowy wynik całej czynności.
Kolejnymi elementami diagramu są konektory, czyli małe okrągłe bloczki, umożliwiające łączenie oddalonych od siebie obiektów. Konektory są uzupełniającymi składnikami diagramu aktywności, poprawiającymi jego czytelność.
Można powiedzieć, że konektory to swego rodzaju „portale” dla sterowania.

W diagramie aktywności można uwzględnić jeszcze sygnały oraz tory pływackie (swimlines). Te pierwsze (przedstawiane jako przerywane linie ze strzałkami) obrazują przesyłanie informacji pomiędzy różnymi wykonawcami danej czynności. Tory pływackie (w postaci ramek) pokazują, które z czynności przypisane są danemu wykonawcy.

W przestawionym przykładzie tory pływackie to okienka oznaczone jako Program 1 i Program 2. Bloczki w okienku Program 1 wykonywane są przez Program 1, a bloczki w Program 2 wykonywane są przez Program 2. Tory pływackie mogą mieć fragmenty wspólne – jeśli tor nazwiemy: Program 1, Program 2, oznaczać to będzie, że daną akcję lub czynność mogą wykonać obydwa programy. Program 1 oraz Program 2 możemy nazywać aktorami.
Bloczek z napisem Uruchom program służy do przesyłania sygnału, który może mieć więcej niż jedno wyjście. W przykładzie stworzyliśmy nowy węzeł sterowania. Oznacza to, że obie czynności wykonywane są asynchronicznie – w przeciwieństwie do opisanej wcześniej współbieżności, która wykonuje się synchronicznie. Przerywana strzałka oznacza, że wysyłany jest sygnał, a nie, że węzeł sterowaniawęzeł sterowania przechodzi w prawo.
Okrąg ze znakiem X oznacza zakończenie węzła sterowania. Należy pamiętać, że każdy węzeł musi się gdzieś kończyć – w przeciwnym razie będzie on sformułowany niepoprawnie. Węzeł może zakończyć się czynnością lub właśnie takim „martwym punktem”.
Diagram pakietów
Przyjrzyjmy się diagramowi pakietów. Składa się on z pakietów, których elementami mogą być między innymi:
inne pakiety,
klasyklasy.
Istnieje wiele innych elementów, które mogą się w diagramie pakietów znaleźć, jednak wymienione dwa są najistotniejsze.
W klasach wpisanych w diagram pakietu nie definiujemy metod. Jest to spowodowane faktem, że do definiowania klas wykorzystujemy diagram klas, który stworzymy na podstawie diagramu pakietów.
Istnieje kilka różnych, równoważnych notacji tych diagramów, jednak omówimy tylko jedną konwencję.
Jeśli chcesz poznać inne notacje, poszukaj w internecie informacji o diagramach pakietów. Rzetelne materiały na ten temat można znaleźć na stronach uczelni wyższych oferujących kierunki informatyczne, ponieważ prowadzi się tam przedmioty związane z projektowaniem oprogramowania. Bardzo dobre omówienia diagramów (wraz z przykładami) znajdziesz między innymi na stronach Akademii Górniczo‑Hutniczej czy Polsko‑Japońskiej Akademii Technik Komputerowych.
Diagram pakietów charakteryzuje wyraźne oddzielenie od siebie poszczególnych komponentów oprogramowania. Przykładowo: Pies i Buda to nazwy pakietów. Jeśli wymienimy cały pakiet Pies na innego Psa, to ten będzie wiedział, jak posługiwać się Budą. Analogicznie, jeśli wymienimy Budę, to Pies również sobie poradzi.

Takie właśnie jest założenie diagramu pakietów – podzielenie programu na kilka komunikujących się ze sobą pakietów, które są niezależne.
Dzięki takiemu podziałowi możemy edytować jedną z funkcji w programie bez obawy, że popsujemy coś w innym miejscu, które jest pośrednio zależne od tej funkcji.

Zamówienie oraz Realizacja zamówienia to klasy, zatem – jak już wcześniej wspomnieliśmy – nie definiujemy ich metod. Zakładamy, że klasa stanowi kompletną całość.
W diagramie pakietów możemy zaznaczać również zależności pomiędzy poszczególnymi klasami, jednak należy to robić tylko w ramach poszczególnych pakietów. Warto dodać, że te elementy także powinniśmy uwzględnić w diagramie klas.
Pomiędzy poszczególnymi pakietami mogą istnieć inne zależności. W tym e‑materiale omówimy tylko podstawowe dziedziczenie, które działa analogicznie do dziedziczenia klas.

Przedstawiony zapis oznacza, że Pakiet A dziedziczy po Pakiecie B, przejmując wszystkie klasy, jakie były w nim umieszczone. Dodatkowo możemy definiować zakres wzajemnej widoczności pakietów, jednak w tym wypadku nie będziemy tego robić, ponieważ nie jest to kluczowe.
Omawiając poszczególne diagramy, wspomnieliśmy niektóre elementy jedynie pobieżnie. Wynika to z faktu, że diagramy można rozbudowywać, ale nie przy każdym projekcie zachodzi taka potrzeba.
Warto pamiętać, że inżynieria oprogramowaniainżynieria oprogramowania, a dokładniej: projektowanie oprogramowania, jest bardzo złożonym procesem. Nie sposób omówić wszystkich jego aspektów, nie tracąc jednocześnie z oczu głównego celu tej serii e‑materiałów, jakim jest stworzenie gry.
Projekt Snake
Zacznijmy od diagramu aktywności. Gracz wykonuje pewne czynności, które mogą być katalizatorami innych zależności, dlatego też schemat będzie większy od poprzednich. Skupmy się na tym, co poszczególne akcje gracza spowodują lub będą mogły powodować.

Dla uproszczenia tworzymy czynność Pojawienie się węża, której użyjemy w kolejnych diagramach. Składa się ona z dwóch kolejno wykonywanych akcji: pojawienia się głowy węża na środku ekranu oraz skierowania głowy węża „na północ”.

Tworzenie diagramu jest procesem. Jesteśmy w stanie ocenić, czy czegoś w nim brakuje, dopiero gdy go skończymy (lub po przejściu do rysowania kolejnej czynności). Jeśli się zorientujemy, że czegoś w diagramie nie uwzględniliśmy, powinniśmy go poprawić. Diagram aktywności przypomina pod tym względem programowanie.
Diagram przedstawiający czynność poruszania się węża nie uwzględnia zatrzymania ruchu, gdy zostanie włączona pauza. Błąd ten wymaga korekty.
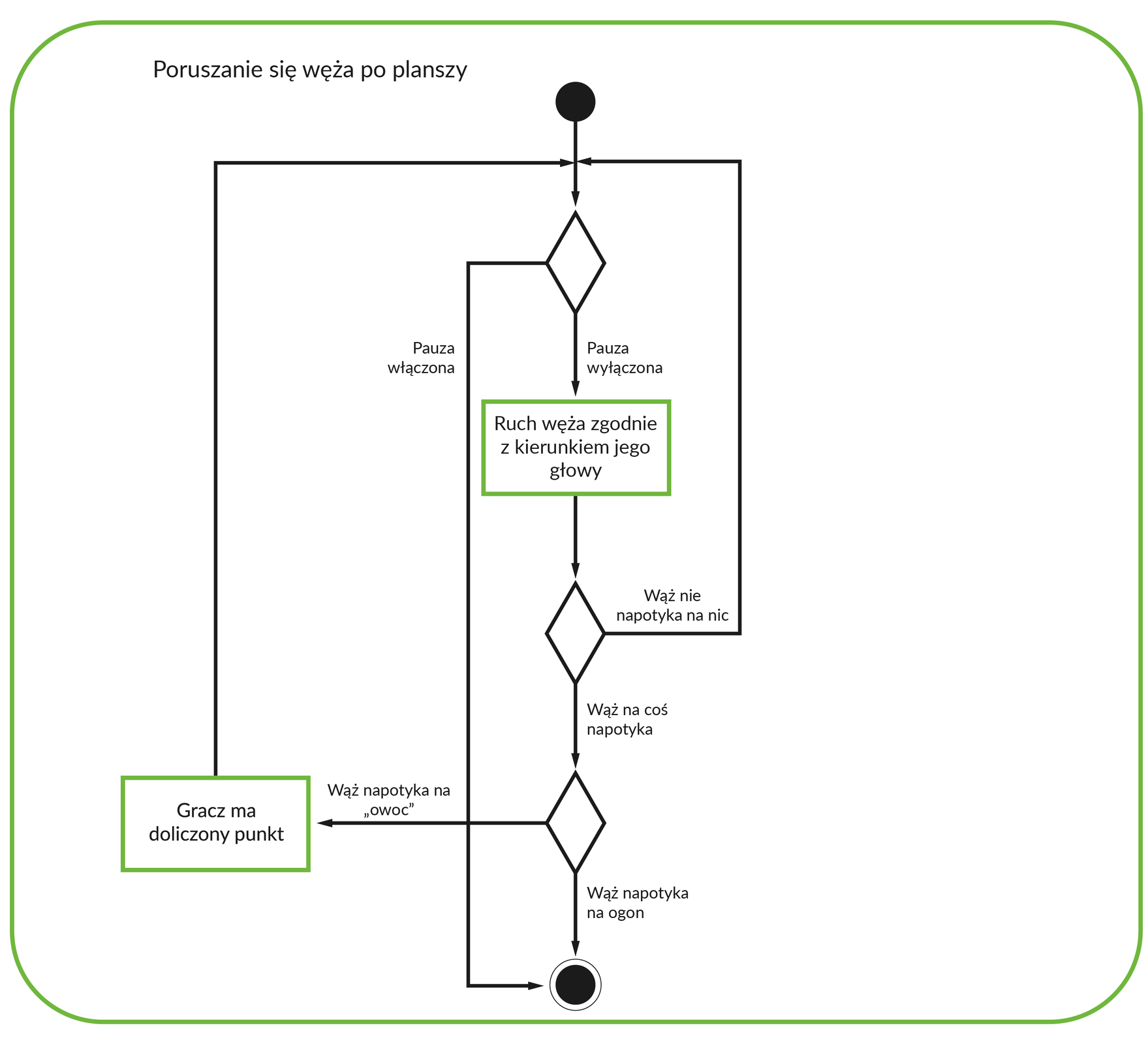
Zapisaliśmy kilka czynności, na podstawie których możemy stworzyć kod. Diagram aktywności możne przywodzić na myśl pseudokod zapisany w formie schematu blokowego – jednak to nie jest to samo i należy o tym pamiętać.

Kolejny diagram prezentuje rozgrywkę z uwzględnieniem współbieżnego sterowania. W grze Snake wąż nie oczekuje, aż klikniemy przycisk. Porusza się niezależnie od naszych akcji.

Diagram wyjaśnia funkcjonowanie rozgrywki, uwzględniając aktywności zarówno użytkownika, jak i samej gry. Przejdźmy do stworzenia diagramu pakietów. Będzie on prosty, ponieważ sama gra ma nieskomplikowaną strukturę.

Na koniec warto zaznaczyć, że wszystkie trzy pakiety powinny mieć swobodny dostęp do siebie nawzajem.
Słownik
proces polegający na stosowaniu podejścia inżynierskiego do tworzenia oprogramowania; wiedza techniczna, które obejmuje każdą fazę życia oprogramowania – od zaprojektowania go, przez implementację, konserwację, a ostatecznie powstanie gotowego produktu
blok kodu definiujący lub częściowo definiujący zachowania oraz dopuszczalny stan obiektów
miejsce, z którego dalej wykonuje się dane akcje bądź czynności i się je śledzi; pierwszy węzeł sterowania pojawia się na samym początku diagramu aktywności