Przeczytaj

Doświadczenie losowe kilkuetapowe wygodnie jest zilustrować za pomocą drzewa doświadczenia losowego (drzewa stochastycznego). Możemy w ten sposób graficznie przedstawić przebieg i wyniki doświadczenia.

Rysunek rozpoczynamy od punktu, zwanego startem (korzeniami drzewa). Wyniki kolejnych etapów doświadczenia to węzły. Odcinki, które łączą dwa kolejne węzły to krawędzie. Każdy końcowy węzeł to wierzchołek drzewa (zatem drzewo może mieć kilka wierzchołków!). Kolejne krawędzie łączące początek drzewa z jednym z wierzchołków to gałąź drzewa. Każdej gałęzi odpowiada jeden wynik doświadczenia wieloetapowego.

Przykład 1

Zbudujemy drzewo stochastyczne dla rzutu monetą.

R11dVnZa4Y532

Schemat składa się z trzech punktów. Punkt pierwszy to start. Odchodzą od niego w dół dwa ukośne rozgałęzienia, które podpisano słownie jako krawędź, a liczbowo jako 0,5., gdyż liczby te określają prawdopodobieństwo dla danej drogi. Lewe rozgałęzienie, czyli krawędź prowadzi do drugiego punku opisanego jako O. Prawe rozgałęzienie prowadzi do punktu opisanego jako R. O oraz R są wierzchołkami.

Drzewo składa się z dwóch gałęzi, odpowiadających wynikom $O$ (orzeł), $R$ (reszka). Na każdej gałęzi zapisane jest prawdopodobieństwo zajścia danego zdarzenia (czyli wyrzucenia orła bądź reszki).

Przykład 2

Budujemy drzewo stochastyczne dla dwukrotnego rzutu monetą.

R1M0SHPILYhEF

Schemat składa się z siedmiu wierzchołków i sześciu krawędzi. Opisuje on dwa rzuty monetą i przebiega przez wszystkie możliwości, jednak ścieżkę nas interesującą oznaczono innym kolorem. Z górnego wierzchołka odchodzą dwie krawędzie o prawdopodobieństwie 0,5. Jest to pierwszy rzut, w którym możemy wylosować orła albo reszkę.Lewa krawędź prowadzi do wierzchołka O, czyli do orła i rozgałęzia się dalej na dwie możliwości w drugim rzucie: po lewej O o prawdopodobieństwie 0,5, po prawej R z takim samym prawdopodobieństwem. Z pierwszego wierzchołka prawa krawędź prowadzi do wierzchołka R - jest to pierwszy rzut - i dalej z wierzchołka R mamy kolejne rozgałęzienie z jednakowym prawdopodobieństwem 0,5 na lewo na wierzchołek O, na prawo na wierzchołek R. Mamy więc cztery możliwości losowań: pierwsza: orzeł, orzeł, druga orzeł reszka, trzecia i ta jest wyróżniona kolorem: reszka, orzeł, czwarta reszka, reszka. Od podpisu reszka, orzeł poprowadzono w dół pionową strzałkę do obliczeń. Obliczono tu prawdopodobieństwo losowania najpierw reszki, a następnie orła. Można to zapisać wzorem: p=0,5·0,5=0,25

Aby obliczyć prawdopodobieństwo na przykład wyrzucenia za pierwszym razem reszki, a za drugim orła (na rysunku tą sytuację ilustruje gałąź pomarańczowa), mnożymy liczby zapisane przy pomarańczowych krawędziach.

Przykład 3

W urnie znajdują się cztery kule fioletowe i sześć niebieskich. Wyciągamy losowo jedną kulę, zapisujemy jej kolor i z powrotem wrzucamy do urny. Następnie wyciągamy losowo drugą kulę. Obliczymy prawdopodobieństwo, że za pierwszym razem wyciągniemy kulę niebieską, a za drugim fioletową.

Zilustrujemy przebieg doświadczenia za pomocą drzewa.

R6n1bMqSBds5d

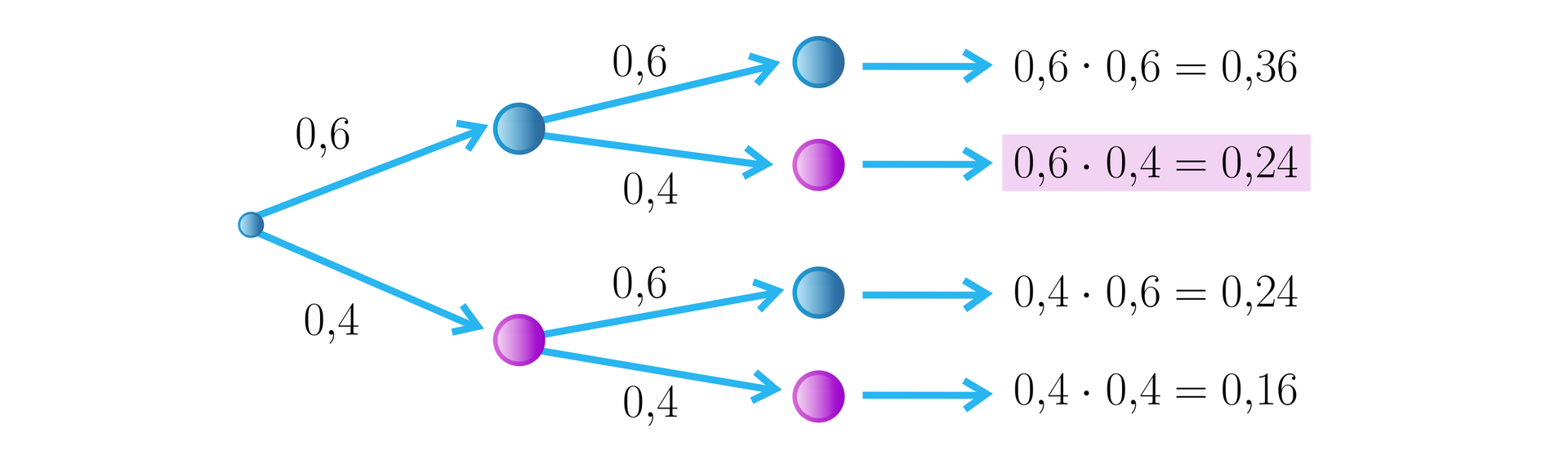
Schemat poziomy przedstawia cztery możliwe ścieżki losowania dwuetapowego. Z wierzchołka odchodzą dwie krawędzie: górna biegnie do niebieskiej kulki i ma prawdopodobieństwo 0,6, dolna biegnie do fioletowej kulki i ma prawdopodobieństwo 0,4. Stąd odchodzą dwie kolejne krawędzie. Górna biegnie do niebieskiej kulki i ma prawdopodobieństwo 0,6, dolna biegnie do fioletowej kulki i ma prawdopodobieństwo 0,4. Najniżej położone rozgałęzienie, czyli losowanie fioletowa, fioletowa opisane jest równaniem: 0,4·0,4=0,16. Wyżej położona ścieżka z losowaniami fioletowa, niebieska jest opisana równaniem: 0,4·0,6=0,24. Idąc od pierwszego wierzchołka górnym rozgałęzieniem, kiedy z prawdopodobieństwem 0,6 losujemy niebieską kulką, mamy dalej kolejne rozgałęzienie – na fioletową kulkę niższe, z prawdopodobieństwem 0,4 oraz wyższe z prawdopodobieństwem 0,6 prowadzące do niebieskiej kulki. To niższe, gdy losowanie przebiega następująco: niebieska, fioletowa, opisane jest równaniem: 0,6·0,4=0,24 i wyróżnione jest kolorem. Najwyżej narysowane odgałęzienie to losowanie niebieska, niebieska opisane równaniem 0,6·0,6=0,36.

Przy każdej krawędzi zapisaliśmy prawdopodobieństwo zajścia danego zdarzenia. Zauważmy, że

$0, 36 + 0, 24 + 0, 24 + 0, 16 = 1$ ,

czyli suma prawdopodobieństw zapisanych przy wierzchołkach krawędzi wychodzących z jednego korzenia jest równa $1$ .

Zdarzenie: za pierwszym razem wylosowaliśmy kulę niebieską, a za drugim fioletową, zilustrowane jest za pomocą dwóch krawędzi tej samej gałęzi. Prawdopodobieństwo zdarzenia obliczamy, mnożąc liczby zapisane przy krawędziach tej gałęzi.

$p = 0, 6 \cdot 0, 4 = 0, 24$

Odpowiedź:

Prawdopodobieństwo, że za pierwszym razem wyciągniemy kulę niebieską, a za drugim fioletową, jest równe $0, 24$ .

Wiemy już, że prawdopodobieństwo zdarzenia jednoelementowego reprezentowanego przez daną gałąź jest równe iloczynowi prawdopodobieństw wypisanych obok krawędzi tej gałęzi. Ten sposób wyznaczania prawdopodobieństwa zdarzeń jednoelementowych w wieloetapowych doświadczeniach, nazywamy regułą mnożenia prawdopodobieństw dla drzewa stochastycznegoregułą mnożenia prawdopodobieństw dla drzewa stochastycznego.

Reguła mnożenia prawdopodobieństw dla drzewa stochastycznego

Reguła: Reguła mnożenia prawdopodobieństw dla drzewa stochastycznego

Prawdopodobieństwo zdarzenia jednoelementowego reprezentowanego przez daną gałąź drzewa, jest równe iloczynowi prawdopodobieństw przyporządkowanych krawędziom, z których składa się rozważana gałąź.

Jeżeli zbiór wszystkich zdarzeń elementarnych wieloetapowego doświadczenia składa się z $n$ elementów, to liczba gałęzi drzewa sporządzonego dla tego doświadczenia jest równa $n$ ( $n \in ℕ_{+}$ ).

Przykład 4

W urnie znajduje się $n$ ( $n \geq 2$ , $n \in ℕ$ ) kul pomarańczowych i $8$ kul zielonych. Losujemy dwie kule bez zwracania. Wiedząc, że prawdopodobieństwo wylosowania dwóch kul pomarańczowych jest równe $\frac{10}{23}$ , obliczymy ile jest wszystkich kul.

Tworzymy model graficzny doświadczenia.

R1BEicxTN7oay

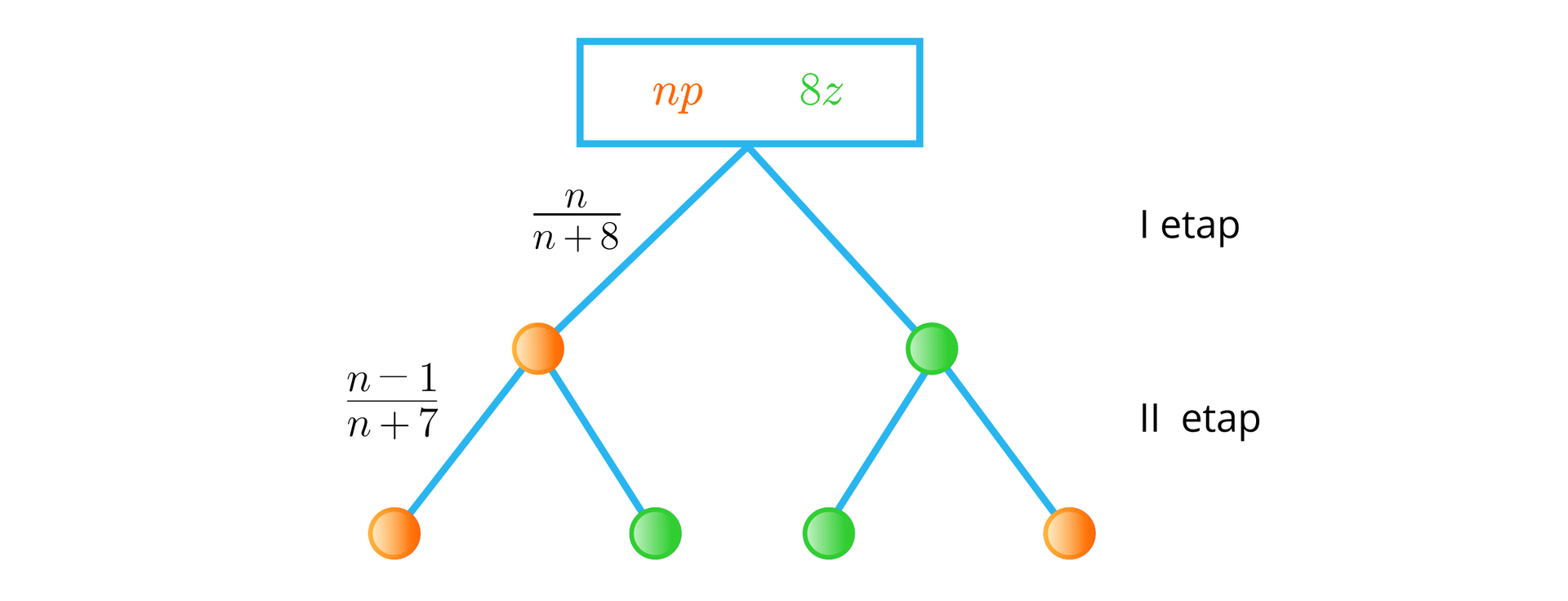
Pionowy schemat losowań zaczyna się w górnej części prostokątem, w który wpisano: np 8z. Stąd poprowadzono dwa odgałęzienia symbolizujące pierwszy etap losowania. Prawa odnoga prowadzi do zielonej kulki, a w kolejnym etapie z tej kulki odchodzą dwa kolejne odgałęzienia na zieloną i pomarańczową kulkę. Etap drugi przebiega następująco. Idąc lewą ścieżką od prostokąta, w pierwszym etapie krawędź prowadzącą do pomarańczowej kulki mamy opisaną jako nn+8. Krawędź ta prowadzi do kulki zielonej i pomarańczowej, przy czym krawędź prowadząca do pomarańczowej opisana jest następująco: n-1n+7.

Tym razem odpowiednie prawdopodobieństwa zapisaliśmy tylko przy interesujących nas krawędziach.

W urnie jest $n$ kul pomarańczowych. W $I$ etapie losujemy kulę pomarańczową spośród $n + 8$ wszystkich kul znajdujących się w urnie.

Teraz w urnie jest już tylko $n + 7$ kul, w tym $n - 1$ pomarańczowych. W $II$ etapie losujemy więc kulę pomarańczową spośród $n + 7$ kul.

Odczytujemy z drzewa, że prawdopodobieństwo wylosowania dwóch kul pomarańczowych jest równe

$\frac{n}{n + 8} \cdot \frac{n - 1}{n + 7}$ .

Na podstawie treści zadania zapisujemy równanie (patrz: reguła mnożenia prawdopodobieństw dla drzewa stochastycznegoreguła mnożenia prawdopodobieństw dla drzewa stochastycznego):

$\frac{n}{n + 8} \cdot \frac{n - 1}{n + 7} = \frac{10}{23}$

Przekształcamy zapisane równanie, otrzymując równanie kwadratowe.

$23 n^{2} - 23 n = 10 \cdot (n^{2} + 15 n + 56)$

$13 n^{2} - 173 n - 560 = 0$

Rozwiązujemy równanie.

$\sqrt{∆} = 243$

$n_{1} = \frac{173 - 243}{26} < 0$ – nie spełnia warunków zadania

$n_{2} = \frac{173 + 243}{26} = 16$

Obliczamy ile jest wszystkich kul: $16 + 8 = 24$ .

Odpowiedź:

W urnie są $24$ kule.

Nie zawsze prawdopodobieństwo danego zdarzenia jest reprezentowane przez jedną gałąź. Korzystamy wtedy z reguły sum.

Reguła sum dla drzewa stochastycznego

Reguła: Reguła sum dla drzewa stochastycznego

Prawdopodobieństwo zdarzenia opisanego przez kilka gałęzi drzewa jest równe sumie prawdopodobieństw otrzymanych zgodnie z regułą mnożenia dla tych gałęzi.

Przykład 5

Rzucamy dwiema monetami. Jeżeli wpadnie co najmniej jeden orzeł – losujemy osobę z klasy $IV A$ . W przeciwnym wypadku losujemy osobę z klasy $IV B$ . W klasie $IV A$ jest ośmiu chłopców i są dwie dziewczyny, w klasie $IV B$ jest dwunastu chłopców i osiem dziewcząt. Obliczymy prawdopodobieństwo wylosowania chłopca.

Tworzymy model graficzny doświadczenia.

R99HHGR3vaVHh

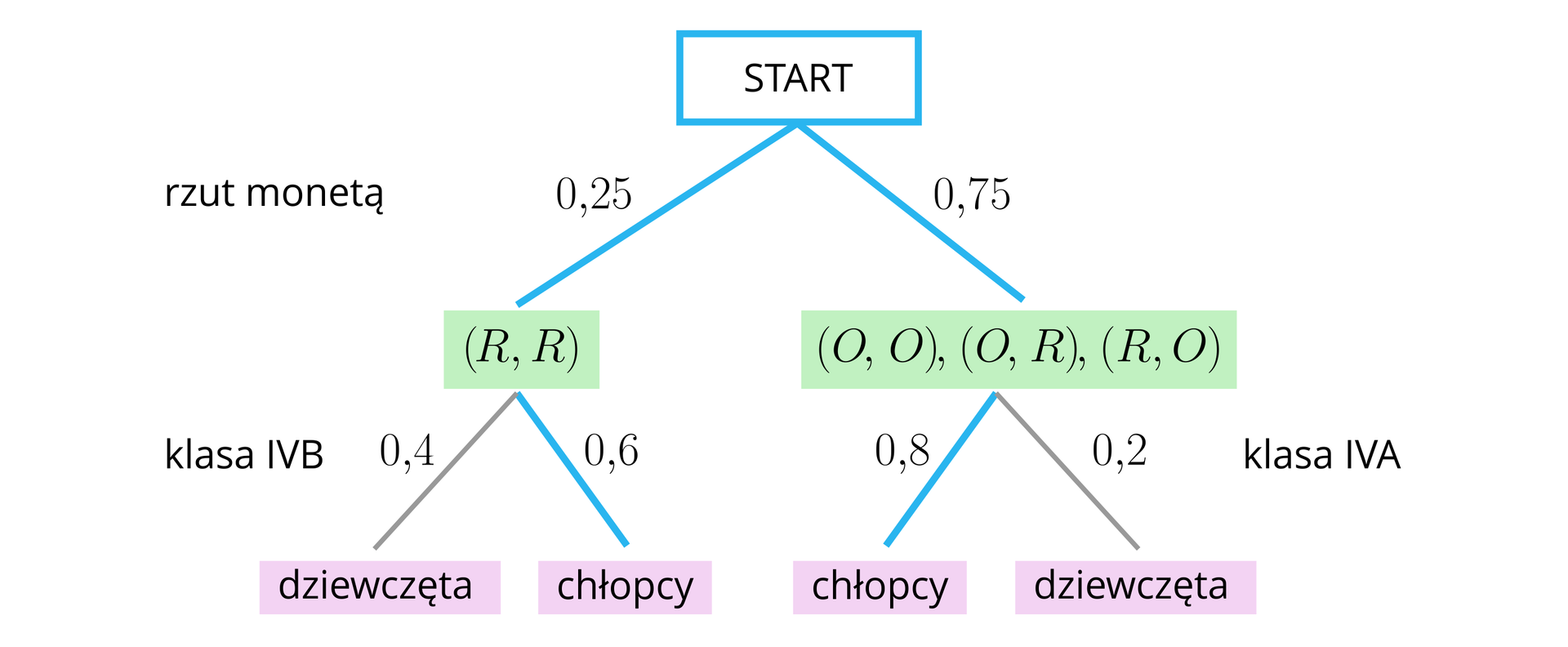
Model graficzny rozpoczyna się napisem START, od którego odchodzą dwie krawędzie: lewa opisana jako 0,25 do wierzchołka (R, R) i prawa opisana jako 0,75 do wierzchołka (O, O), (O, R), (R, O). Jest to część modelu opisująca rzut monetą. Dalsze odgałęzienia opisują wybór z klas. Z wierzchołka (R, R) mamy dwie możliwości: wybór dziewcząt z klasy czwartej B z prawdopodobieństwem 0,4 oraz wybór chłopców z klasy czwartej B z prawdopodobieństwem 0,6. Z wierzchołka z co najmniej jednym orłem, czyli (O, O), (O, R), (R, O), mamy kolejne dwie możliwości: wybór chłopców z klasy czwartej A z prawdopodobieństwem 0,8 oraz wybór dziewcząt z klasy czwartej A z prawdopodobieństwem 0,2.

Zaznaczamy na niebiesko gałęzie, na których opisane jest interesujące nas zdarzenie. Żeby obliczyć prawdopodobieństwo zdarzenia $A$ – wylosowano chłopca, najpierw mnożymy liczby zapisane wzdłuż niebieskich krawędzi na każdej z gałęzi, a następnie dodajemy otrzymane liczby.

$P (A) = 0, 25 \cdot 0, 6 + 0, 75 \cdot 0, 8 = 0, 15 + 0, 6 = 0, 75$

Odpowiedź:

Prawdopodobieństwo wylosowania chłopca jest równe $0, 75$ .

W przypadku, gdy doświadczenie składa się z kilku etapów, na drzewie stochastycznym można zaznaczać tylko gałęzie obrazujące rozpatrywane doświadczenie.

Przykład 6

Prawdopodobieństwo, że jutro będzie padał śnieg jest równe $0, 3$ . W każdym innym dniu, jeśli pada śnieg, prawdopodobieństwo, że będzie padał śnieg następnego dnia jest równe $\frac{3}{5}$ . Jeśli śnieg nie pada prawdopodobieństwo, że śnieg będzie padać następnego dnia jest równe $\frac{1}{10}$ . Obliczymy prawdopodobieństwo, że śnieg będzie padać popojutrze.

Jeśli prawdopodobieństwo tego, że śnieg będzie padał następnego dnia, jest równe $\frac{3}{5}$ , czyli $(0, 6)$ , to prawdopodobieństwo tego, że śnieg nie będzie padał jest równe $1 - 0, 6 = 0, 4$ .

Jeśli śnieg nie pada w danym dniu, prawdopodobieństwo, że śnieg będzie padać następnego dnia jest równe $\frac{1}{10} = 0, 1$ , to prawdopodobieństwo tego, że śnieg nie będzie padał jest równe $1 - 0, 1 = 0, 9$ .

Sporządzamy drzewo prawdopodobieństwa, na którym zaznaczymy tylko przydatne gałęzie.

R1cuybWo6GQRO

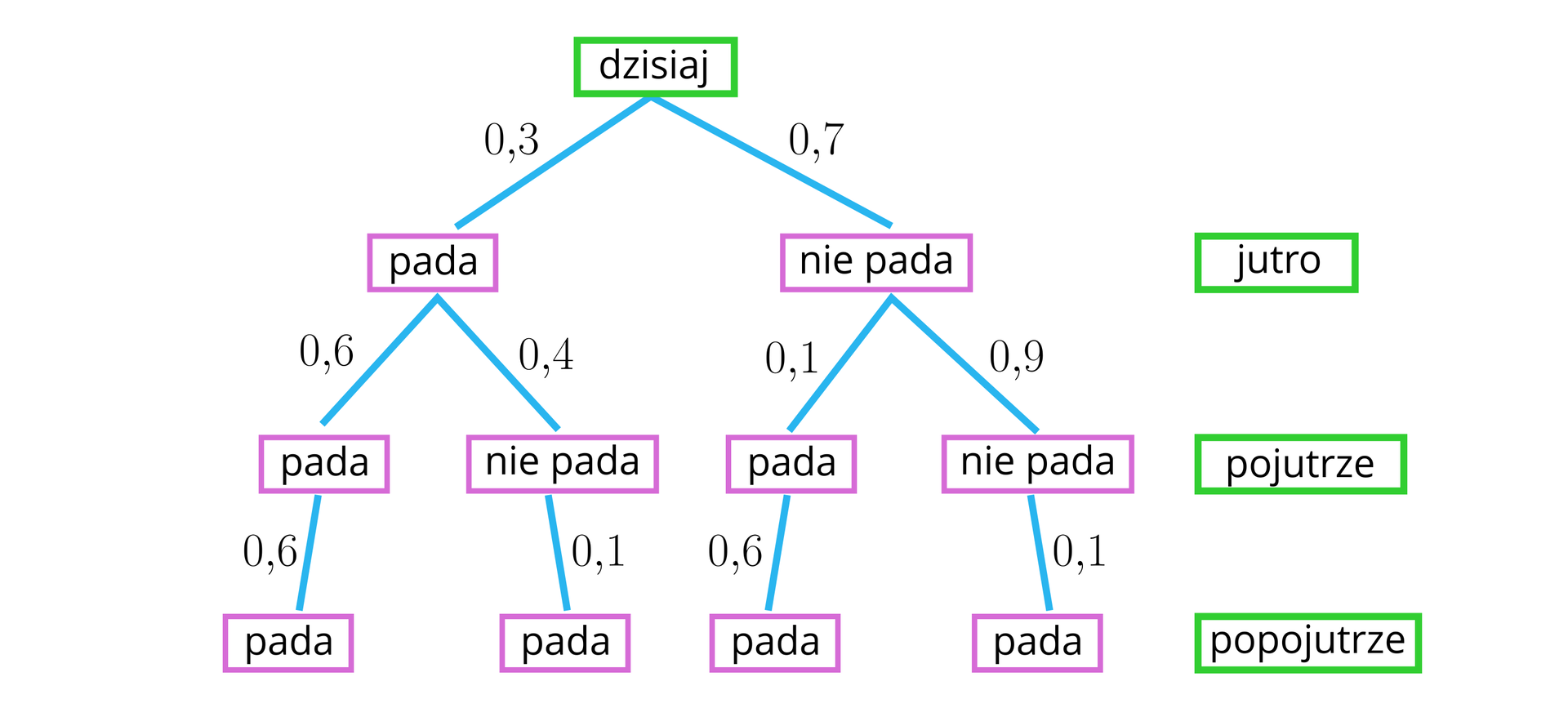
Drzewo rozpoczyna się nagłówkiem dzisiaj, od którego odchodzą dwie gałęzie dotyczące jutrzejszej pogody: pada z prawdopodobieństwem 0,3 i nie pada z prawdopodobieństwem 0,7. Jeśli jutro będzie padać, to pojutrze będzie padać z prawdopodobieństwem 0,6 i nie będzie padać z prawdopodobieństwem 0,4. Jeśli pojutrze będzie padać, to popojutrze będzie padać z prawdopodobieństwem 0,6, jeśli nie będzie, to popojutrze będzie padać z prawdopodobieństwem 0,1. Teraz zajmijmy się drugim rozgałęzieniem. Jeśli jutro nie będzie padać, to mamy dwie kolejne gałęzie: pojutrze będzie padać z prawdopodobieństwem 0,1 i wtedy popojutrze będzie padać z prawdopodobieństwem 0,6 i jeśli pojutrze nie będzie padać, to z prawdopodobieństwem 0,9 i wtedy popojutrze będzie padać z prawdopodobieństwem 0,1.

Obliczając prawdopodobieństwo, skorzystamy z reguły sum.

$p = 0, 3 \cdot 0, 6 \cdot 0, 6 + 0, 3 \cdot 0, 4 \cdot 0, 1 + 0, 7 \cdot 0, 1 \cdot 0, 6 + 0, 7 \cdot 0, 9 \cdot 0, 1$

$p = 0, 225$

Odpowiedź:

Prawdopodobieństwo tego, że popojutrze będzie padał śnieg jest równe $p = 0, 225$ .

Słownik

reguła mnożenia prawdopodobieństw dla drzewa stochastycznego

prawdopodobieństwo zdarzenia jednoelementowego reprezentowanego przez daną gałąź drzewa, jest równe iloczynowi prawdopodobieństw przyporządkowanych krawędziom, z których składa się rozważana gałąź

Wprowadzenie

Infografika

Słownik