Przeczytaj

Promień okręgu opisanego na trójkącie prostokątnym

Wiemy, że w okręgu miara kąta wpisanego jest dwa razy mniejsza od miary kąta środkowego opartego na tym samym łuku. Prostą konsekwencją tego twierdzenia jest wniosek, iż każdy kąt wpisany oparty na półokręgu jest prosty, a w konsekwencji, że przeciwprostokątna dowolnego trójkąta prostokątnego jest średnicą okręgu opisanego na tym trójkącie.

R9wluGmsbug5G

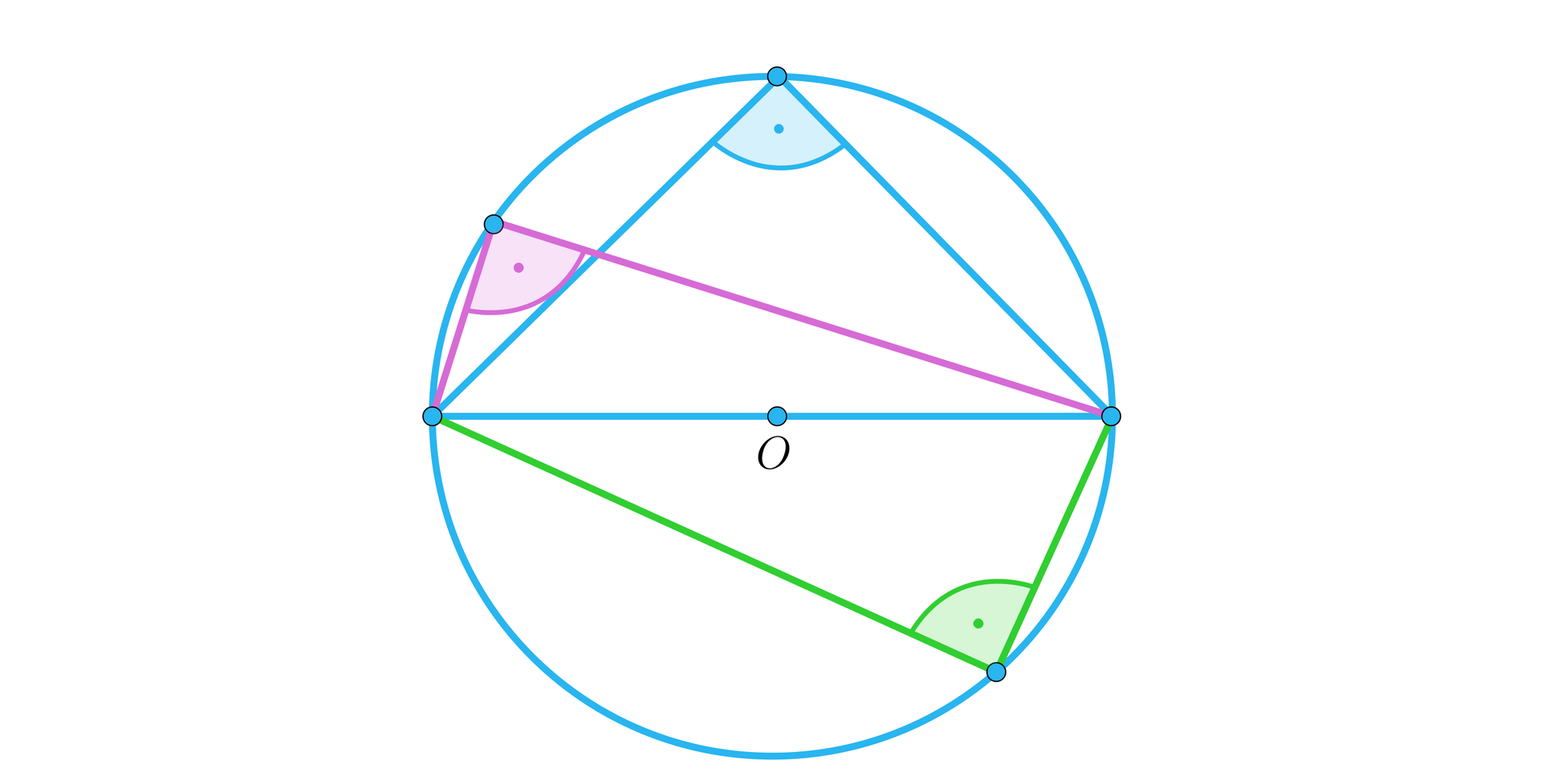
Ilustracja przedstawia okrąg o środku w punkcie O opisany na trzech trójkątach prostokątnych, które posiadają wspólną przeciwprostokątną, a ich wierzchołki przy kącie prostym leżą w różnych częściach okręgu. — Trójkąty rozpięte na średnicy okręgu.

o okręgu opisanym na trójkącie prostokątnym

Twierdzenie: o okręgu opisanym na trójkącie prostokątnym

Promień $R$ okręgu opisanego na trójkącie prostokątnym o przeciwprostokątnej $c$ ma długość równą $R = \frac{1}{2} c$ .

Promień okręgu wpisanego w trójkąt prostokątny

Rozważmy trójkąt prostokątny $A B C$ o przeciwprostokątnej $A B$ . Przez $P$ , $Q$ , $R$ oznaczmy punkty, w których okrąg o środku $O$ i promieniu $r$ , wpisany w ten trójkąt, jest styczny do odpowiednich boków trójkąta, jak na rysunku.

RyyD22eVRNEbf

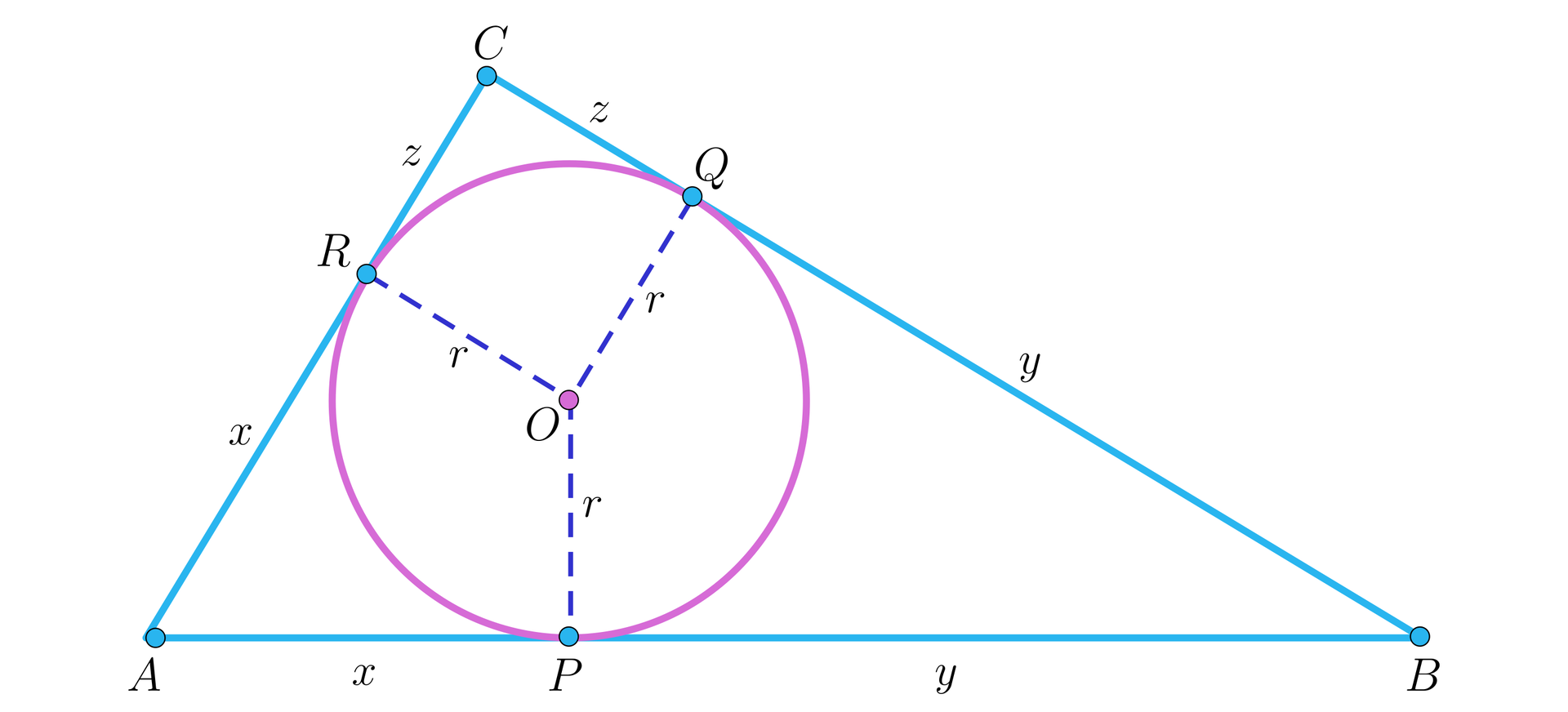
Ilustracja przedstawia okrąg o środku O wpisany w trójkąt prostokątny ABC. Punkty styczności okręgu z ramionami trójkąta to R, Q i P. Odcinek AR i AP mają długość x, odcinki CR i CQ mają długość z, a odcinki BP i BQ mają długość y. Odcinki PO,RO, QO mają długość r. — Promień okręgu wpisanego.

Z zasadniczego twierdzenia planimetriizasadnicze twierdzenie planimetriizasadniczego twierdzenia planimetrii (twierdzenia o odcinkach stycznych) wynika równość odpowiednich odcinków, co pozwala przyjąć oznaczenia: $|A P| = |A R| = x$ , $|B P| = |B Q| = y$ oraz $|C Q| = |C R| = z$ .

Czworokąt $C R O Q$ jest kwadratem, zatem $z = r$ .

Przyjmijmy: $|A B| = c$ , $|B C| = a$ , $|A C| = b$ . Wtedy: $|A B| = c = x + y$ , $|B C| = a = y + z$ , $|A C| = b = x + z$ , stąd $c = x + y = (b - z) + (a - z)$ . Zatem $c = a + b - 2 z$ , czyli $z = \frac{a + b - c}{2}$ . Ale $z = r$ , stąd promień okręgu wpisanego w trójkąt prostokątny o przeciwprostokątnej $c$ i przyprostokątnych $a$ , $b$ ma długość $r = \frac{a + b - c}{2}$ .

Ostatnia równość pozwala sformułować poniższe twierdzenie.

o sumie średnic

Twierdzenie: o sumie średnic

Suma długości przyprostokątnych w trójkącie prostokątnym jest równa sumie długości średnic dwóch okręgów: opisanego i wpisanego w ten trójkąt.

Dowód

Niech $R$ , $r$ oznaczają odpowiednio promień okręgu opisanego i promień okręgu wpisanego w trójkąt prostokątny o przeciwprostokątnej $c$ i przyprostokątnych $a$ , $b$ . Wtedy $r = \frac{a + b - c}{2}$ . Ponieważ $c = 2 R$ , więc $r = \frac{a + b - 2 R}{2}$ . Stąd $2 r = a + b - 2 R$ , czyli $2 R + 2 r = a + b$ . Co było do udowodnienia.

Przykład 1

Wyznaczymy teraz pole trójkąta prostokątnego w zależności od długości promieni $R$ , $r$ okręgów opisanego i wpisanego w ten trójkąt.

Rozwiązanie

Na wstępie przyjmijmy, że przyprostokątne trójkąta mają długości $a$ , $b$ , a pole tego trójkąta oznaczmy przez $P$ .

Wiemy, że $2 R + 2 r = a + b$ . Podnosząc stronami zapisaną równość do kwadratu otrzymujemy $4 R^{2} + 8 R r + 4 r^{2} = a^{2} + 2 a b + b^{2}$ .

Ale $a^{2} + b^{2} = c^{2} = {(2 R)}^{2} = 4 R^{2}$ oraz $\frac{1}{2} a \cdot b = P$ , czyli $a \cdot b = 2 P$ .

Zatem $4 R^{2} + 8 R r + 4 r^{2} = 4 R^{2} + 4 P$ . Stąd $P = r^{2} + 2 R r$ .

Przykład 2

Rozważmy trójkąt prostokątny opisany na okręgu o promieniu $r$ i wpisany w okrąg o promieniu $R = 3 r$ . Wyznaczymy długości przyprostokątnych $a$ , $b$ tego trójkąta.

Rozwiązanie

Ponieważ $r = \frac{a + b - c}{2}$ oraz $c = 2 R = 2 \cdot (3 r) = 6 r$ , więc $a + b = 8 r$ . Korzystając z wyniku uzyskanego w Przykładzie 1. możemy zapisać, że $\frac{1}{2} a b = r^{2} + 2 \cdot (3 r) r$ . Stąd $a b = 14 r^{2}$ .

Możemy teraz zapisać układ równań z niewiadomymi $a$ , $b$ : $\{\begin{cases} a b = 14 r^{2} \\ a + b = 8 r \end{cases}$ .

Z drugiego z równań wynika, że $b = 8 r - a$ , stąd $a \cdot (8 r - a) = 14 r^{2}$ . Rozwiążemy teraz równanie kwadratowe z niewiadomą $a$ i parametrem $r$ postaci $a^{2} - 8 r \cdot a + 14 r^{2} = 0$ .

Jego wyróżnik jest równy $∆ = 64 r^{2} - 4 \cdot 14 r^{2} = 8 r^{2}$ .

Stąd $a_{1} = \frac{8 r + 2 \sqrt{2} r}{2} = (4 + \sqrt{2}) r$ , $a_{2} = \frac{8 r - 2 \sqrt{2} r}{2} = (4 - \sqrt{2}) r$ .

Odpowiednio $b_{1} = 8 r - a_{1} = 8 r - (4 + \sqrt{2}) r = (4 - \sqrt{2}) r$ oraz $b_{2} = 8 r - a_{2} = 8 r - (4 - \sqrt{2}) r = (4 + \sqrt{2}) r$ .

Pozostaje zauważyć, że trójkąt spełniający warunki zadania jest wyznaczony jednoznacznie: jedna z jego przyprostokątnych ma długość $(4 - \sqrt{2}) r$ , a druga $(4 + \sqrt{2}) r$ .

Stosunek długości promienia okręgu opisanego na trójkącie do długości promienia wpisanego w dany trójkąt prostokątny

Z nierówności Euleratwierdzenie Euleranierówności Eulera wynika, że jeśli $R$ jest promieniem okręgu opisanego na dowolnym trójkącie, a $r$ jest promieniem okręgu wpisanego w ten trójkąt, to $R \geq 2 r$ , gdzie równość zachodzi tylko dla trójkąta równobocznego. Zatem $\frac{R}{r} \geq 2$ . Warto zbadać iloraz promieni tych okręgów w przypadku trójkąta prostokątnego. W szczególności pozwoli to stwierdzić, że problem postawiony w Przykładzie 2. był dobrze określony. Rozważmy trójkąt prostokątny równoramienny o przeciwprostokątnej $c$ . Wtedy $c = 2 R$ , a każda z przyprostokątnych ma długość $a = \frac{c}{\sqrt{2}} = \frac{2 R}{\sqrt{2}} = R \cdot \sqrt{2}$ . Promień okręgu wpisanego jest więc równy $r = \frac{R \sqrt{2} + R \sqrt{2} - 2 R}{2} = R (\sqrt{2} - 1)$ . Zatem iloraz $\frac{R}{r}$ ma wartość $\frac{R}{R (\sqrt{2} - 1)} = \sqrt{2} + 1$ i jest to najmniejsza wartość, jaką może przyjąć ten iloraz w przypadku trójkąta prostokątnego. Prawdziwe jest zatem następujące twierdzenie.

o ilorazie promieni okręgów w trójkącie prostokątnym

Twierdzenie: o ilorazie promieni okręgów w trójkącie prostokątnym

Niech $R$ będzie promieniem okręgu opisanego na trójkącie prostokątnym, a $r$ niech będzie promieniem okręgu wpisanego w ten trójkąt. Wtedy $\frac{R}{r} \geq \sqrt{2} + 1$ .

Z powyższych rozważań wynika w szczególności, że w trójkącie prostokątnym o przeciwprostokątnej $c$ najmniejsza odległość między środkiem okręgu opisanego na tym trójkącie i środkiem okręgu wpisanego w ten trójkąt jest równa $\frac{(\sqrt{2} - 1) \cdot c}{2}$ .

Słownik

twierdzenie Eulera

w trójkącie kwadrat odległości między środkami okręgów opisanego i wpisanego w ten trójkąt jest równy $R^{2} - 2 R r$ , gdzie $R$ , $r$ są odpowiednio promieniami tych okręgów

zasadnicze twierdzenie planimetrii

odcinki stycznych poprowadzone do danego okręgu z punktu leżącego na zewnątrz okręgu, wyznaczone przez ten punkt i punkty styczności, mają równe długości

Wprowadzenie

Symulacja interaktywna

Promień okręgu opisanego na trójkącie prostokątnym

Promień okręgu wpisanego w trójkąt prostokątny

Stosunek długości promienia okręgu opisanego na trójkącie do długości promienia wpisanego w dany trójkąt prostokątny

Słownik