Przeczytaj
Przedstawianie funkcji wykładniczej warto zacząć od prostego przykładu.
Niektóre szczepy bakterii podwajają rozmiar swojej kolonii co godzinę, o ile umożliwiają to warunki środowiskowe. Zakładając idealne warunki, liczebność populacji w ciągu kilkunastu godzin od umieszczenia pierwszej bakterii w środowisku przedstawia poniższa tabela.
Liczba godzin od | Rozmiar populacji bakterii |
|---|---|
Kolejne wartości w tabeli odpowiadają zatem liczbom , , itd.
Wprowadźmy następującą definicję.
Funkcję zadaną wzorem
gdzie jest pewną dodatnią stałą, nazywamy funkcją wykładniczą.
Nazwa tej charakterystycznej funkcji wynika z opisującego ją wzoru - argument pojawia się tam w roli wykładnikawykładnika potęgi .
Przyjrzyjmy się następującym wykresom.
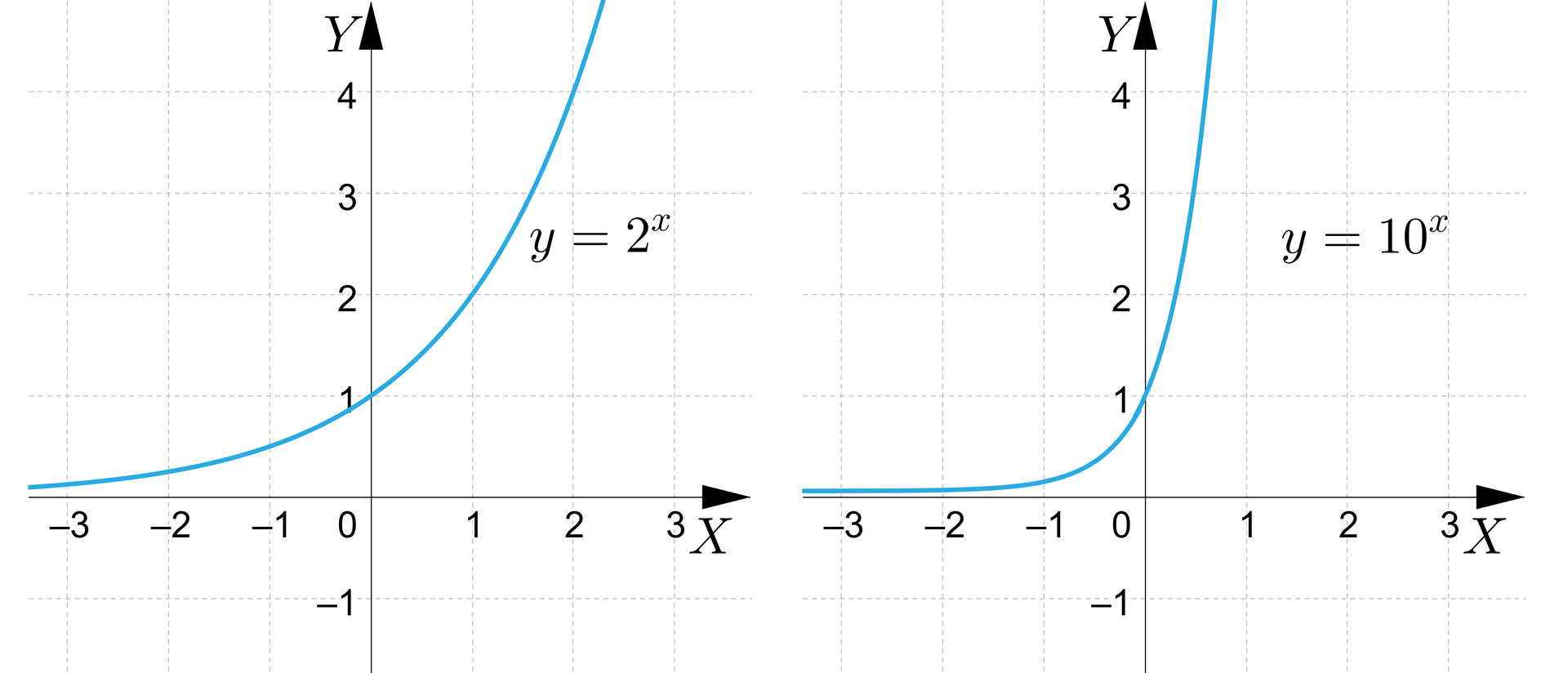
Wykresy tych funkcji są zbliżone do siebie kształtem. Ten kształt okazuje się być typowy dla tych funkcji wykładniczych, których podstawapodstawa jest liczbą większą od . Przy takim założeniu rozpatrywana funkcja wykładnicza jest rosnąca.
Jak będzie jednak wyglądać funkcja wykładnicza, której podstawa jest liczbą z przedziału ? Przypomnijmy, że dla i dla dowolnej liczby rzeczywistej zachodzi równość:
Na postawie tej równości można oczekiwać, że funkcja wykładnicza, której podstawa jest mniejsza od ma wykres będący symetrycznym odbiciem względem osi pewnego wykresu funkcji wykładniczej o podstawie większej niż . Fakt ten zilustrowany został na poniższych wykresach.
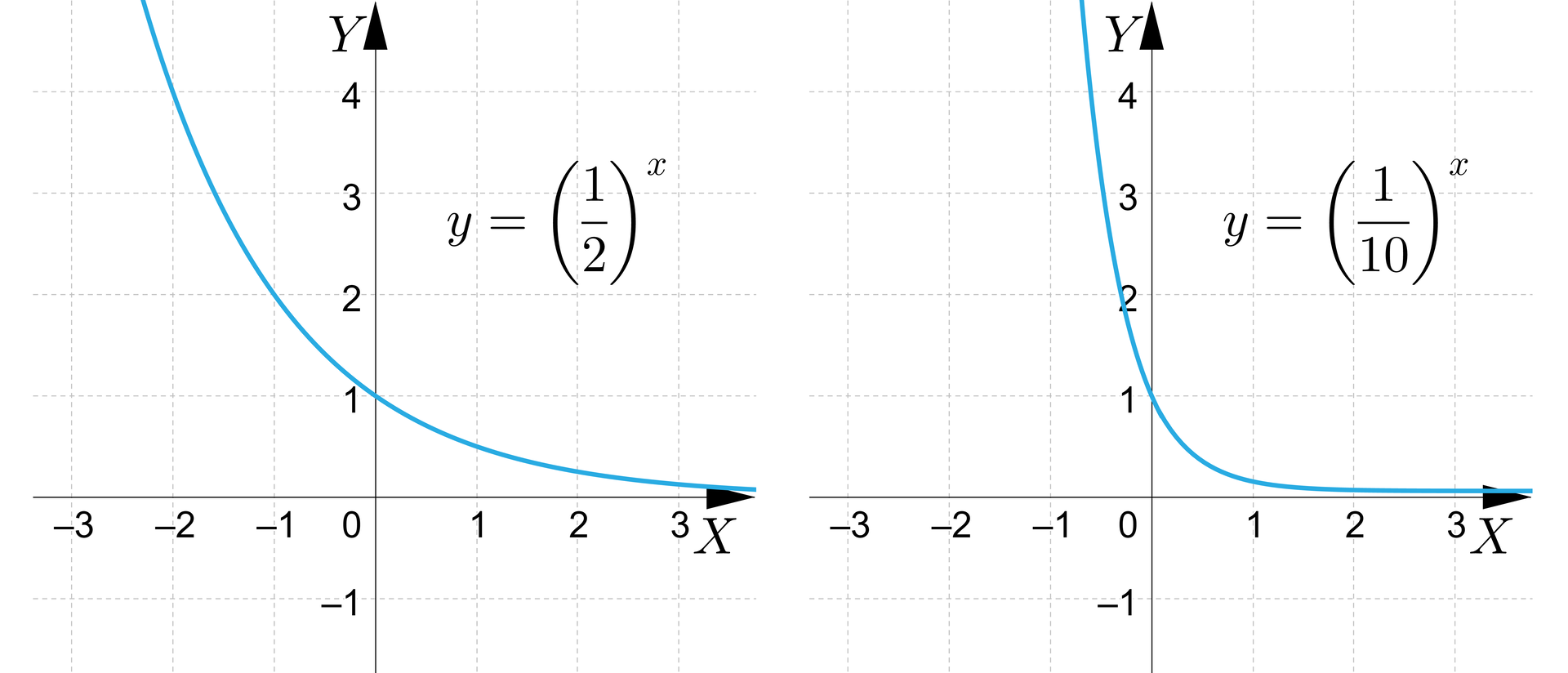
Funkcja wykładnicza bardzo często pojawia się przy matematycznych opisach pewnych naturalnych procesów zachodzących w przyrodzie. Ilustrują to poniższe przykłady.
Populacja muszki owocówki (zakładając nieograniczony dostęp do pożywienia) pięciokrotnie zwiększa swoją liczebność w ciągu jednego tygodnia. Zakładając, że kolonia muszek założona została przez pojedynczą parę owadów, obliczymy jaką liczebność będzie mieć populacja po upływie pięciu tygodni.
Rozwiązanie
Niech oznacza liczbę par muszek w populacji podczas n‑tego tygodnia obserwacji. Wówczas
oraz .
Idąc dalej, w drugim tygodniu populacja składa się z par muszek, zaś po upływie kolejnego tygodnia osiąga liczebność: par.
W czwartym tygodniu jest ich pięciokrotnie więcej, niż w tygodniu trzecim, co daje liczbę par muszek owocówek i w ostatnim tygodniu populacja osiąga wielkość par muszek.
Umieszczenie tych wartości na wspólnym wykresie sprawi, że uzyskamy wykres funkcji wykładniczej .

Ten przykład ilustruje nam, jak niezwykle szybki okazuje się być przyrost opisywany funkcją wykładniczą. Przyjrzyjmy się innemu zjawisku opisywanemu przez tę funkcję.
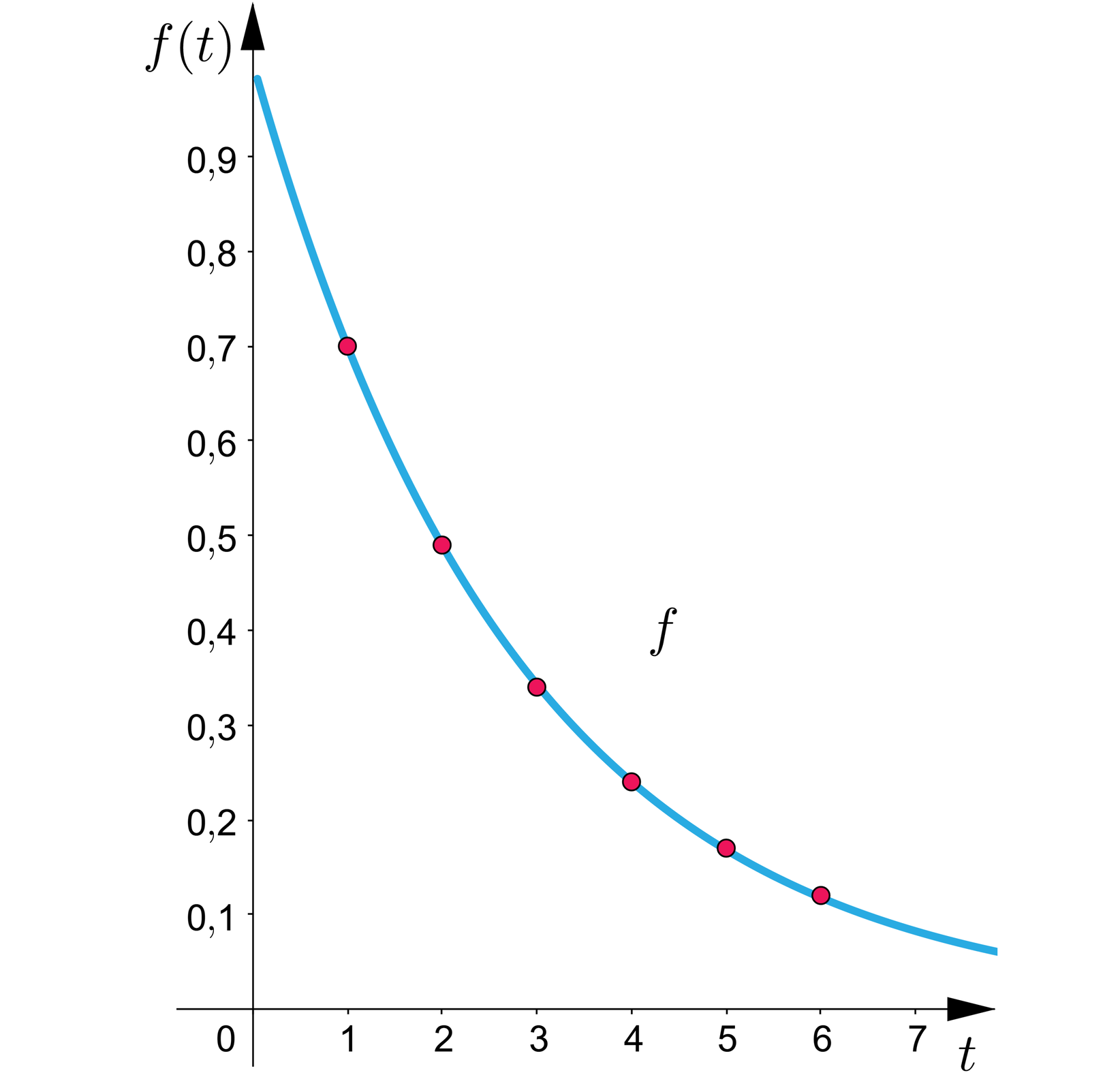
Pewien rodzaj pestycydów stosowany do ochrony roślin uprawnych przed szarańczą ulega rozkładowi w tempie wykładniczym zgodnie z następującą regułą:
ilość pestycydu obserwowana w zbieranych pod koniec danego miesiąca plonach maleje o względem ilości obserwowanej na koniec poprzedniego miesiąca.
Wiedząc, że maksymalne bezpieczne dla człowieka stężenie pestycydu w zbieranych plonach stanowi dawki nagromadzonej w wyniku oprysku, ustalimy po ilu miesiącach od zastosowania pestycydów można bezpiecznie zebrać plony.
Rozwiązanie
Niech opisuje początkową ilość pestycydu obserwowanego w świeżo spryskanych plonach. Przyjmując miesiąc za jednostkę czasu, wartość opisywać będzie ilość pestycydu obserwowaną w plonach po upływie miesięcy. Z treści zadania wynika, że ilość obserwowanego w zbiorach środka ochronnego zmniejsza się do wartości z końca poprzedniego miesiąca. Oznacza to, że
.
Naszym zadaniem jest znalezienie takiej wartości , dla której nie będzie przekraczać . W tym celu obliczamy kilka kolejnych wartości funkcji wykładniczej .
Mamy zatem:
;
;
;
;
.
Ilość pestycydów w plonach dopiero po upływie miesięcy od oprysku spadła poniżej granicznej wartości . Wykładniczy spadek ilości pestycydu obserwowanej w zebranych plonach ilustruje poniższy wykres.
Ostatnim, lecz nie mniej ważnym przykładem funkcji wykładniczej, z którym możemy się spotkać w codziennym życiu, jest oprocentowanie składane.
Bank oferuje lokatę z oprocentowaniem w skali roku. Jaką ilość pieniędzy będziemy mieli po upływie trzech lat (zaokrąglając do pełnych groszy), jeżeli wpłacimy na tę lokatę ?
Rozwiązanie
Zauważmy, że o ile po jednym roku lokata o wartości wzrośnie do wartości , o tyle po dwóch latach nie będzie ona wynosić . Dzieje się tak, ponieważ zarobione na lokacie groszy również będzie generować zyski w kolejnych latach.
Niech . Przypatrzmy się, jakie zyski wytworzy złotówka na takiej lokacie w ciągu dwóch i trzech lat.
Po upływie drugiego roku, na lokacie z pojedynczej złotówki będziemy mieć:
.
Analogicznie, na koniec trzeciego roku wartość złotówki zamrożonej na lokacie wyniesie .
Przemnożenie tej wartości przez kwotę ulokowanego , daje nam
.
Słownik
przy podnoszeniu liczby do potęgi (czyli wykonywaniu operacji ), liczbę potęgowaną nazywamy podstawą
przy podnoszeniu liczby do potęgi liczbę nazywamy wykładnikiem potęgi
sposób naliczania odsetek od zdeponowanego kapitału, w którym odsetki nagromadzone w poprzednich okresach uwzględniane są przy naliczaniu odsetek za okres bieżący