Przeczytaj
Przypomnijmy definicję walca.
Walcem nazywamy bryłę obrotową, która powstaje przez obrót prostokąta wokół osi zawierającej jeden z jego boków.
Pole powierzchni całkowitej walca o promieniu podstawy i wysokości obliczamy ze wzoru
Objętość walca
Niech będzie długością promienia podstawy walca, a jego wysokością.

Wówczas objętość walcawalca obliczamy ze wzoru
Ponieważ podstawa walca jest kołem, zatem objętość walca obliczamy ze wzoru
Wiadomo, że pole powierzchni całkowitej walca wynosi , a promień podstawy walca ma długość . Obliczymy objętość tego walca.
Rozwiązanie
Narysujmy walec i wprowadźmy oznaczenia, jak na rysunku.

Ponieważ promień podstawy walca a pole powierzchni całkowitej walca obliczamy ze wzoru , to do wyznaczenia długości wysokości walca rozwiązujemy równanie:
, czyli .
Wobec tego objętość walca wynosi:
.
Obliczymy, o ile procent zwiększyła się objętość walca, w którym promień podstawy oraz wysokość zwiększono o .
Rozwiązanie
Jeżeli jest długością promienia podstawy walca a jego wysokością, to objętość walca wyraża się wzorem:
.
Jeżeli długości promienia podstawy oraz wysokości walca zwiększymy o , wówczas wielkości te będą wynosiły odpowiednio , oraz , .
Zatem objętość walca będzie wynosiła .
Wobec tego objętość walca zwiększyła się o:
.
Śruba wykonana z mosiądzu ma kształt bryły przedstawionej na poniższym rysunku. Obliczymy masę tej śruby, jeżeli wiadomo, że stopu waży . W obliczeniach przyjmiemy, że .

Rozwiązanie
Zauważmy, że bryła z rysunku zbudowana jest z dwóch walców.
Wprowadźmy następujące oznaczenia:
– długość promienia mniejszego walca,
– długość promienia większego walca,
– długość wysokości mniejszego walca,
– długość wysokości większego walca.
Z rysunku odczytujemy, że:
,
,
,
.
Zatem objętość bryłyobjętość bryły wynosi:
.
Zatem masa tej śruby wynosi:
.
Prostokąt o boku długości i przekątnej długości obracamy wokół osi przechodzącej przez środki dłuższych boków. Obliczymy objętość otrzymanego walca.
Rozwiązanie
Narysujmy prostokąt oraz otrzymany walecwalec, jak na poniższych rysunkach.
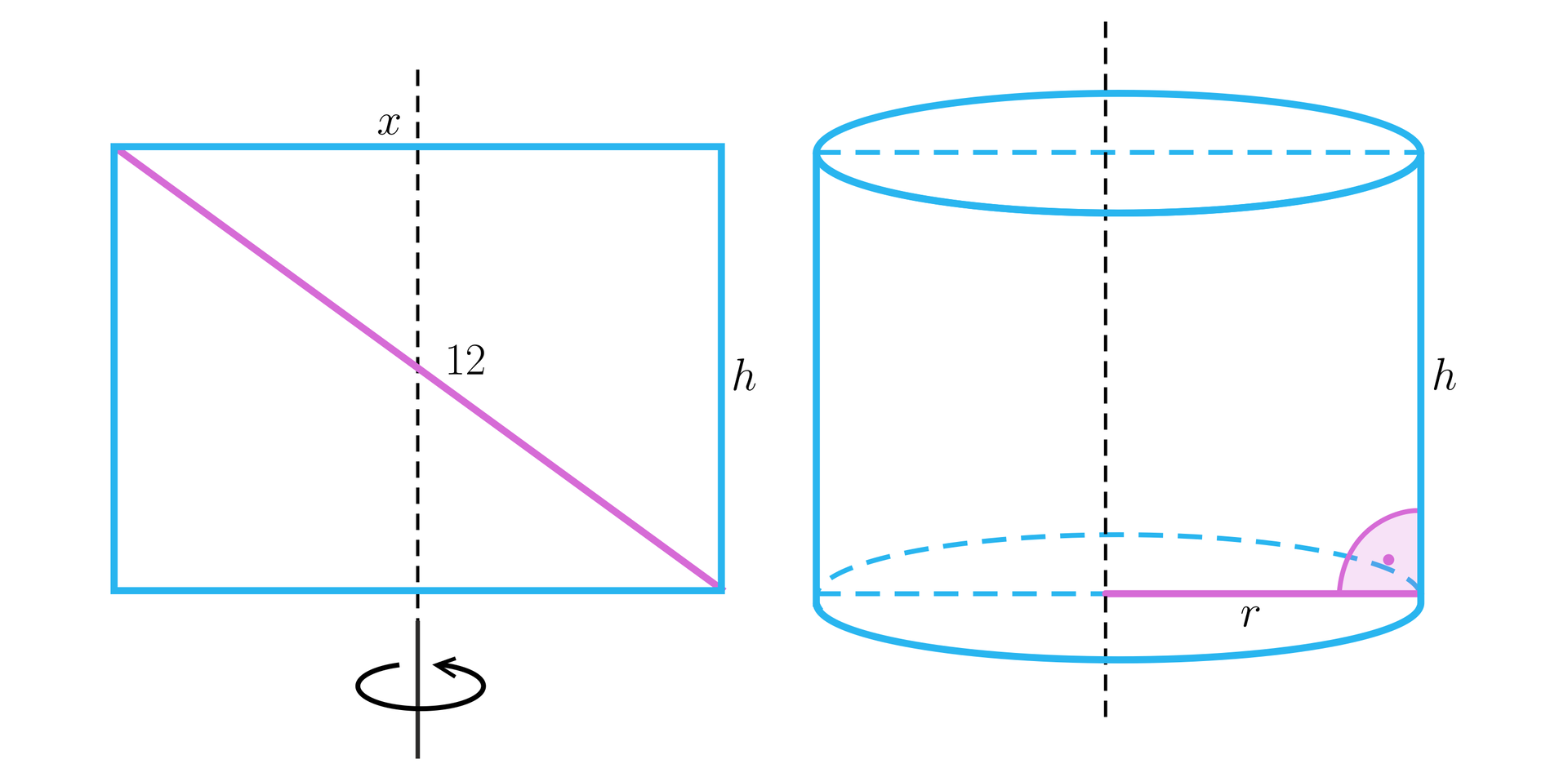
Jeżeli przez oznaczymy długość drugiego boku prostokąta, to do wyznaczenia wartości rozwiązujemy równanie, korzystając z twierdzenia Pitagorasa:
.
Jeżeli jest długością promienia podstawy walca, to , a wysokość walca .
Zatem objętość walca jest równa:
.
Obliczymy objętość walca z poniższego rysunku.

Rozwiązanie
Z rysunku odczytujemy, że promień podstawy .
Do wyznaczenia długości wysokości wykorzystamy twierdzenie Pitagorasa:
.
Wobec tego objętość bryły z rysunku wynosi:
.
Słownik
bryła obrotowa, która powstaje przez obrót prostokąta wokół osi zawierającej jeden z jego boków
ilość sześcianów jednostkowych, jakimi można wypełnić daną bryłę