Przeczytaj
Dane są trójkąty o bokach i kątach jak na poniższym rysunku.
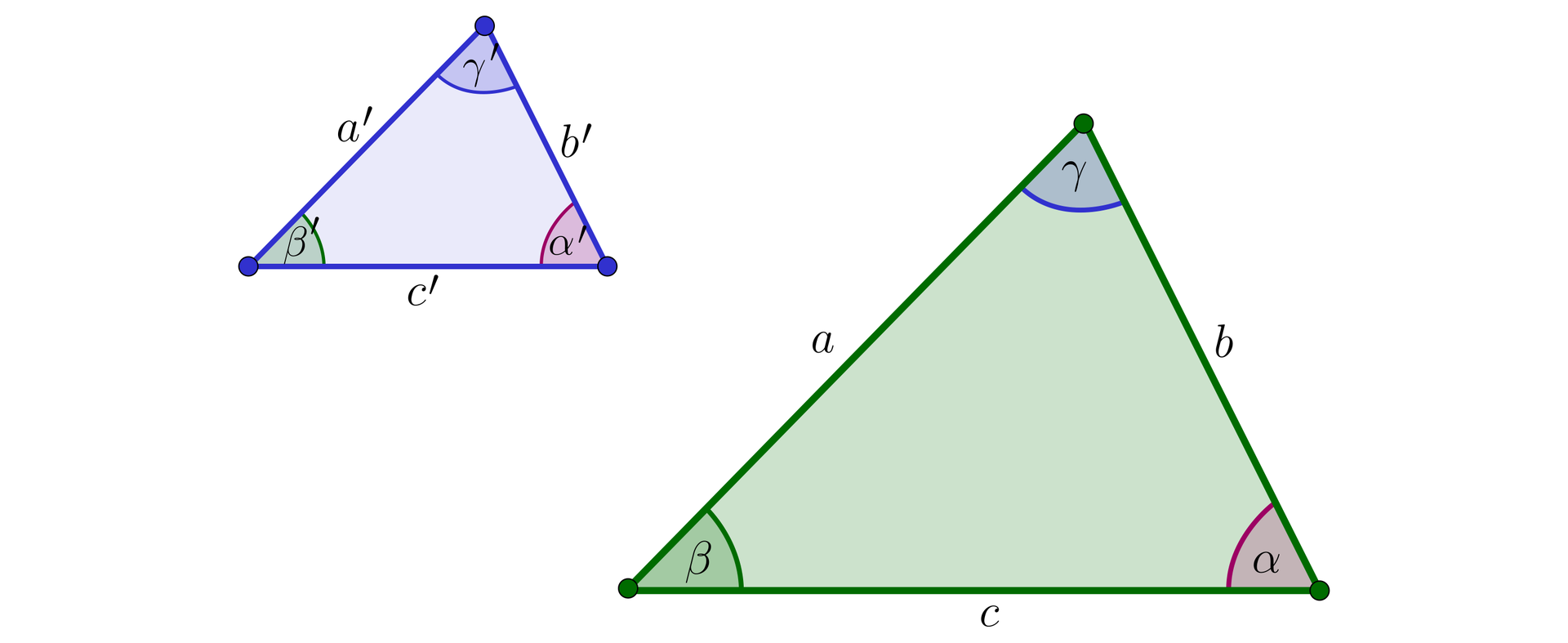
Jeśli zachodzi jedna z poniższych cech podobieństwa:
cecha bok – bok – bok (bbb): stosunki długości par odpowiednich boków są równe, czyli ,
cecha kąt – kąt – kąt (kkk): miary par odpowiednich kątów są równe, czyli , i ,
cecha bok – kąt – bok (bkb): stosunki długości dwóch par boków są równe i miary kątów między tymi bokami są równe, czyli np. i ,
to zachodzą też wszystkie pozostałe, a trójkąty oraz nazywamy podobnymi, co zapisujemy symbolicznie:
.
Stosunek nazywamy skalą tego podobieństwaskalą tego podobieństwa.
Zauważmy, że badając, czy dane dwa trójkąty są podobnepodobne na mocy cechy kkk, wystarczy sprawdzić równość tylko dwóch par kątów. Jeśli np. i , to korzystając z twierdzenia o sumie kątów w trójkącie otrzymujemy, że .
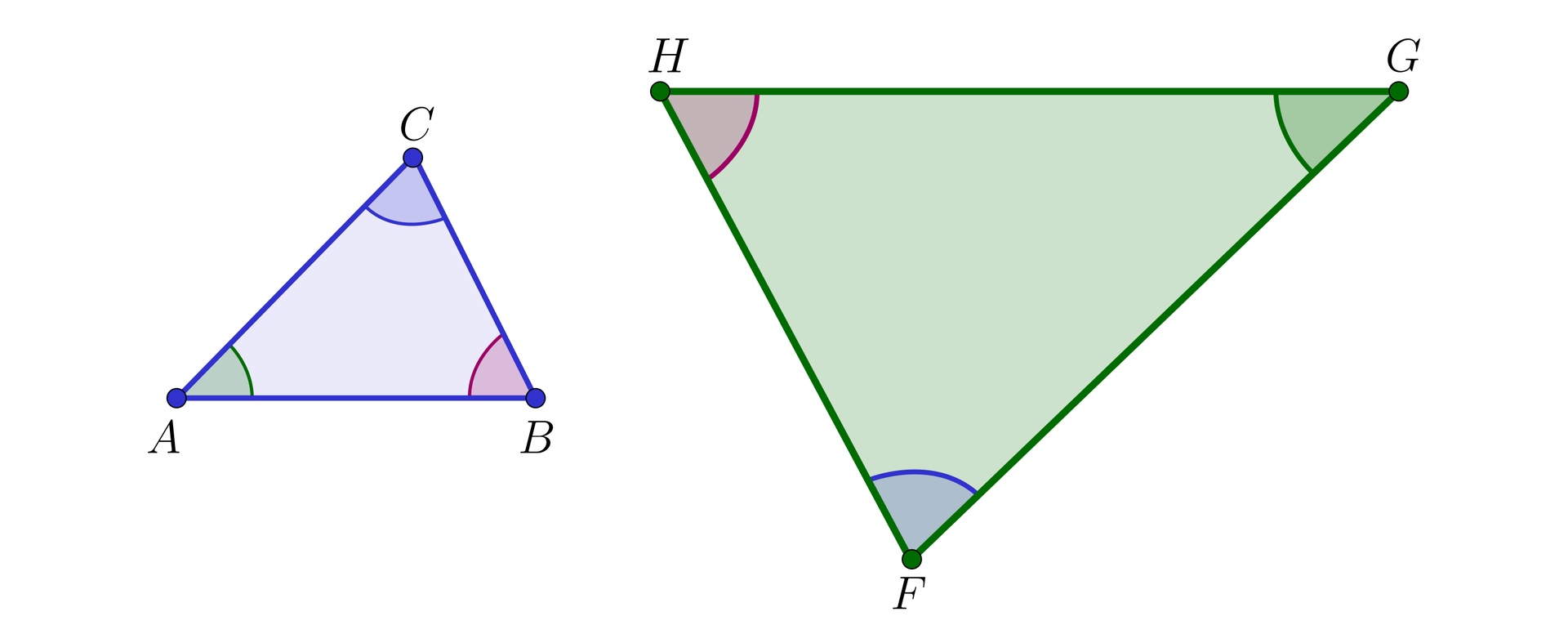
Pisząc o podobieństwiepodobieństwie trójkąta do trójkąta (zobacz rysunek poniżej), warto akcentować porządkiem wierzchołków, że:
kąt przy wierzchołku odpowiada kątowi przy wierzchołku ,
kąt przy wierzchołku – kątowi przy wierzchołku ,
a kąt przy wierzchołku – kątowi przy wierzchołku .
Wtedy informacja, że trójkąt jest podobny do trójkąta w skaliw skali będzie oznaczać, że:
,
,
oraz .
Jeśli dwa trójkąty oraz są podobnepodobne, to stosunek dowolnych dwóch boków w trójkącie jest taki sam jak stosunek odpowiadających im boków w trójkącie .
Na rysunku poniżej stosunek odcinka niebieskiego do zielonego jest taki sam w obu trójkątach podobnychpodobnych oraz .
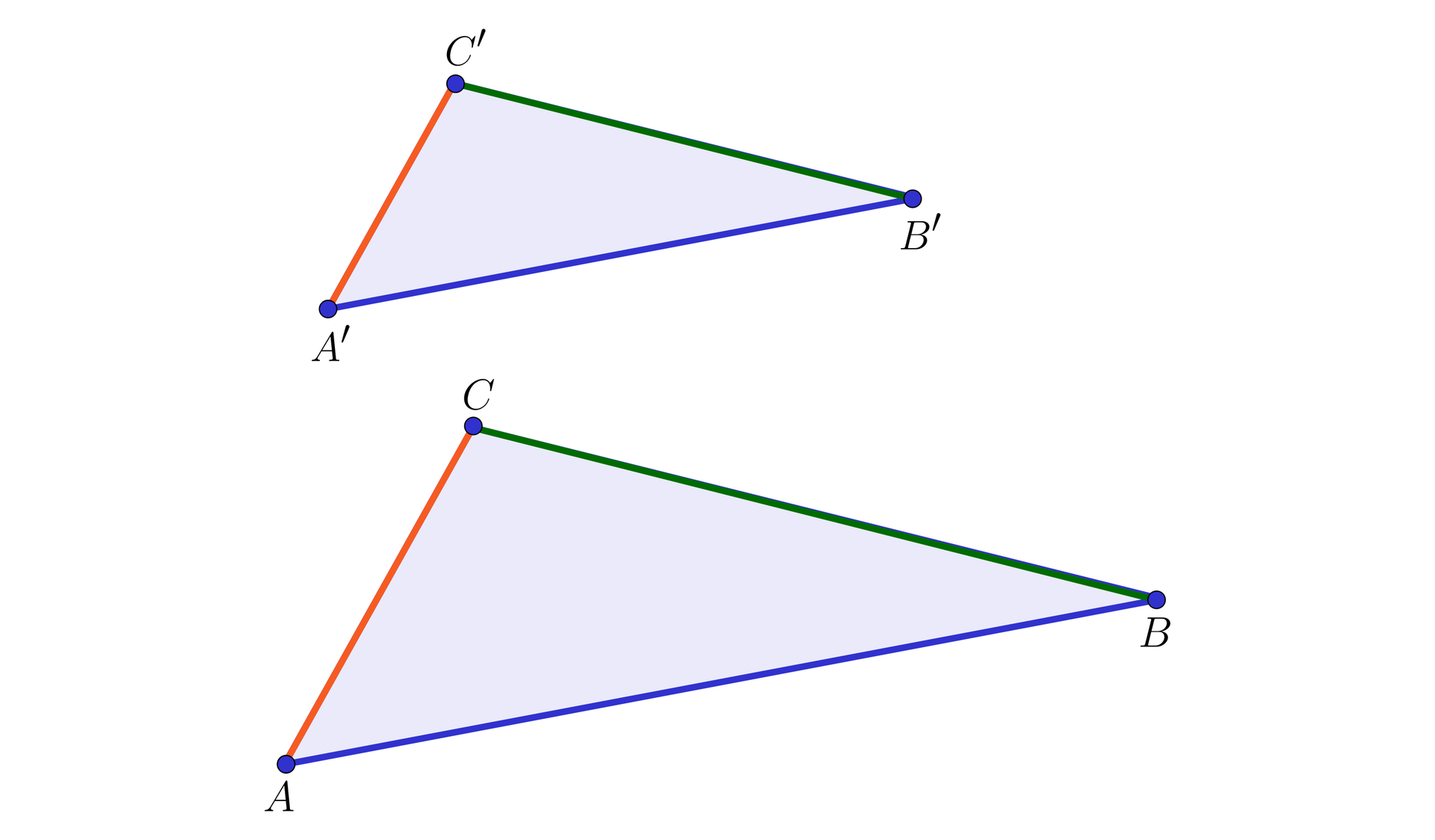
Wynika to stąd, że skoro na mocy podobieństwapodobieństwa trójkątów mamy
,
więc, korzystając z własności proporcji, uzyskujemy
.
Z powyższej uwagi będziemy korzystać równie często, jak z cech podobieństwa.
Na rysunku poniżej odcinki i są równoległe, a ponadto , oraz .
Obliczymy długość odcinka (oznaczamy ).

Rozwiązanie
Zauważamy, że ponieważ , więc równe są pary kątów odpowiadających:
,
.
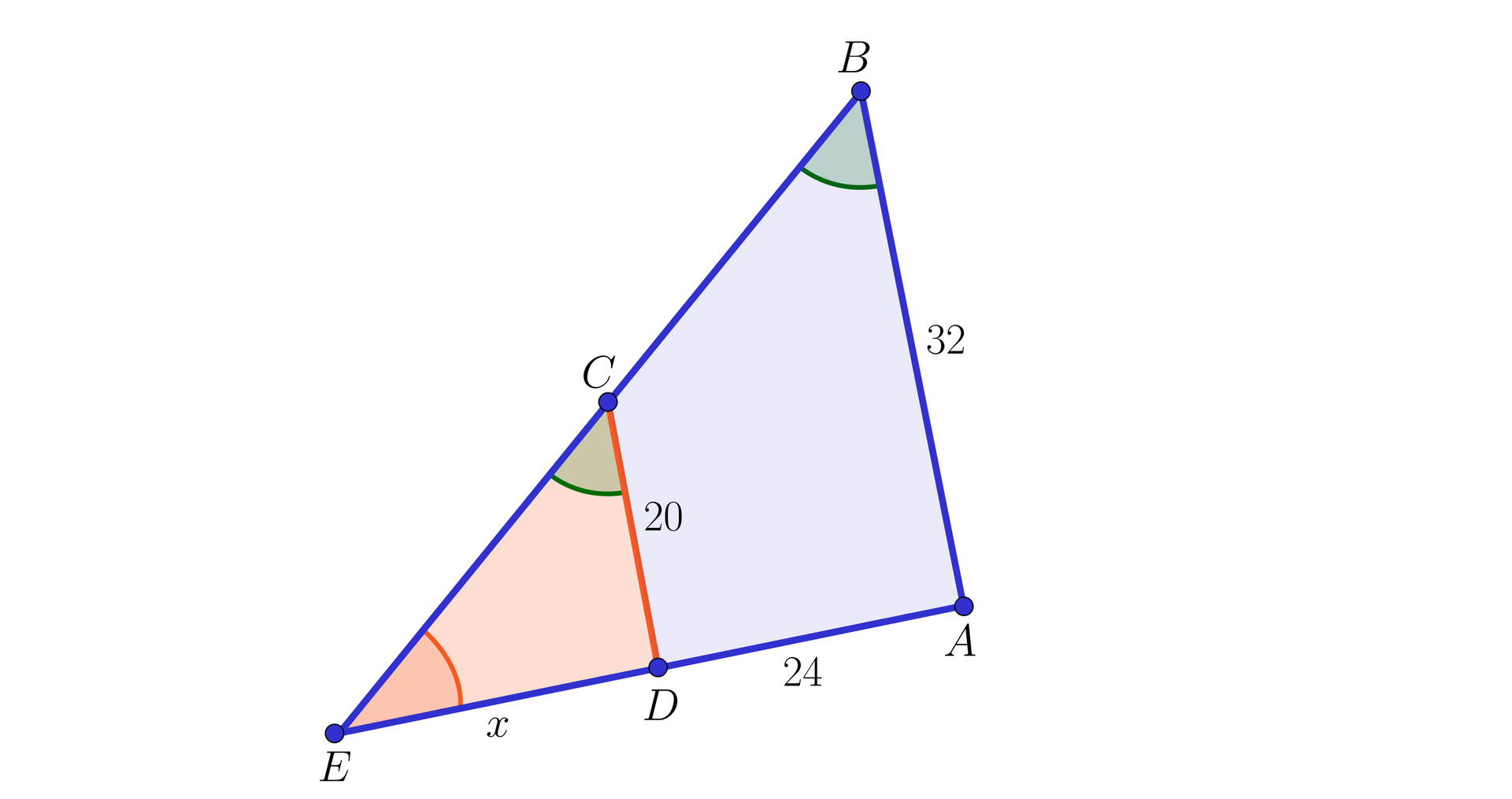
Zatem trójkąty oraz są podobnepodobne, na mocy cechy kkk. Stąd musi też zachodzić cecha podobieństwa bbb.
W szczególności: , to znaczy ,
a więc
czyli .
Odp. Długość odcinka jest równa .
a) W trójkącie równoramiennym wysokość poprowadzona z wierzchołka między ramionami przecina podstawę w punkcie , a wysokość poprowadzona z wierzchołka przecina ramię w punkcie (jak na poniższym rysunku).
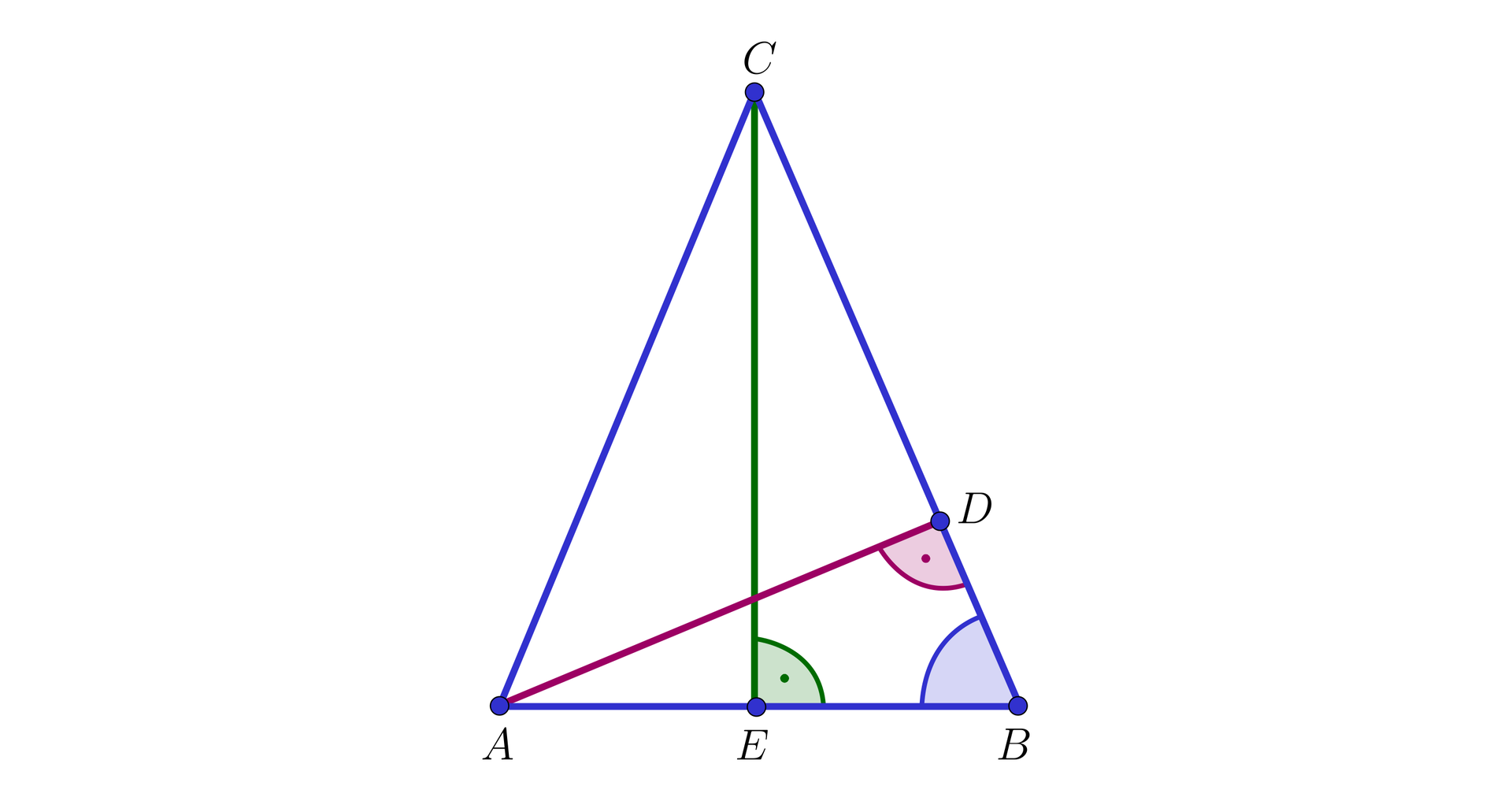
Wtedy trójkąty i są prostokątne i mają wspólny kąt przy wierzchołku , a więc są podobnepodobne, co wynika z cechy podobieństwa kkk. Oznacza to, że prawdziwa jest zależność
.
b) W trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego dzieli ten trójkąt na dwa mniejsze trójkąty, podobnepodobne do trójkąta . Wynika to z cechy podobieństwa kkk.
Przykładowo, trójkąt jest podobnypodobny do trójkąta , bowiem:
kąt przy wierzchołku w trójkącie jest prosty i równy kątowi przy wierzchołku w trójkącie ,
kąt przy wierzchołku jest wspólny dla trójkątów i .
Rp58ih9yISFfv 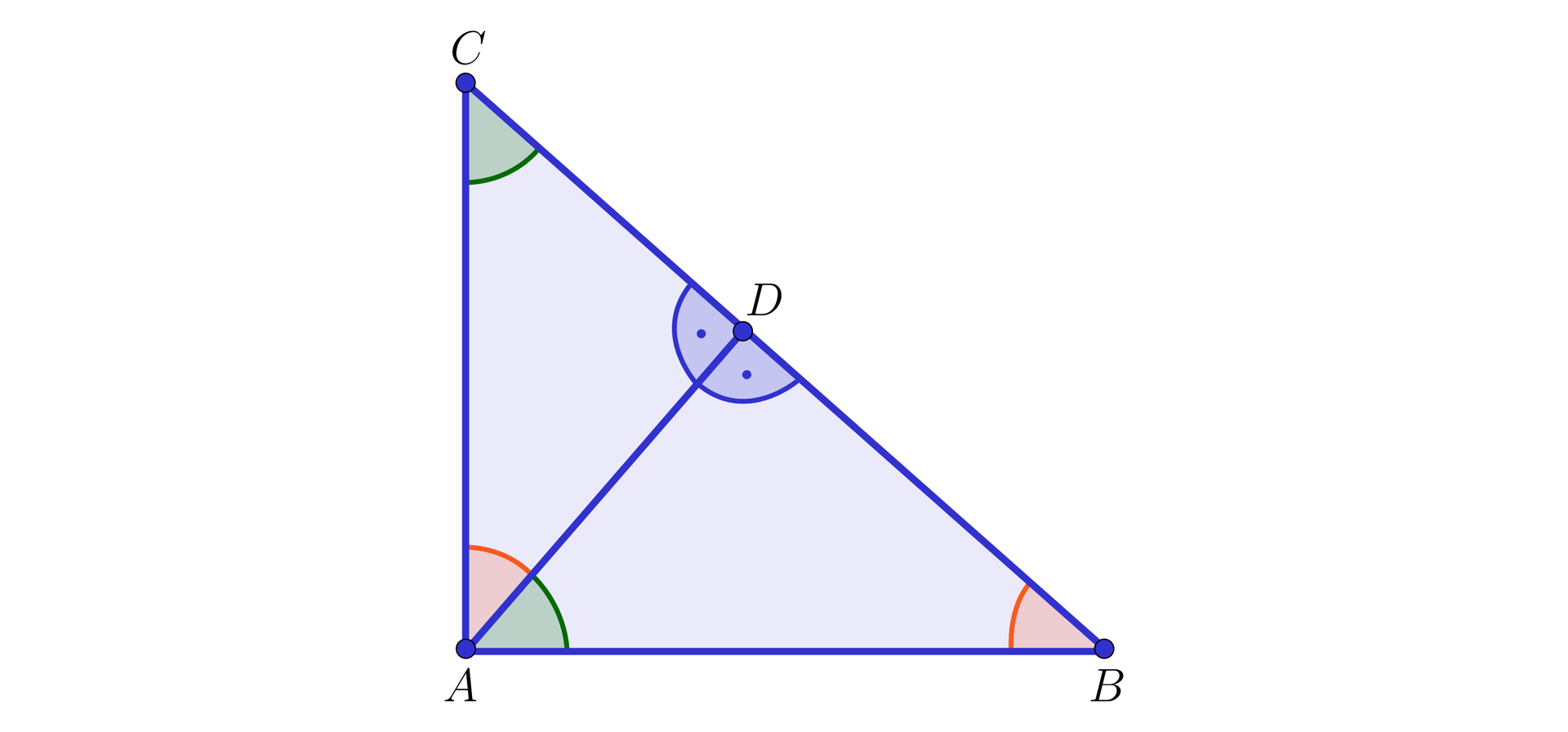
W analogiczny sposób wykazujemy, że trójkąt jest podobnypodobny do trójkąta .
Zauważmy też, że trójkąty oraz również są podobnepodobne (jest to przykład ogólnej prawidłowości: jeśli trójkąt jest podobnypodobny do trójkąta oraz trójkąt jest podobnypodobny do trójkąta , to trójkąty i też są podobnepodobne).
Z podobieństwapodobieństwa trójkątów oraz wynika, że , skąd dostajemy następujący przydatny wniosek:
w trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na takie odcinki oraz , że
.
W trójkącie połączono odcinkiem środki boków i . Trójkąty i są podobnepodobne na mocy cechy bkb, gdyż:
mają wspólny kąt przy wierzchołku oraz
(punkty i dzielą odcinki odpowiednio i na pół).
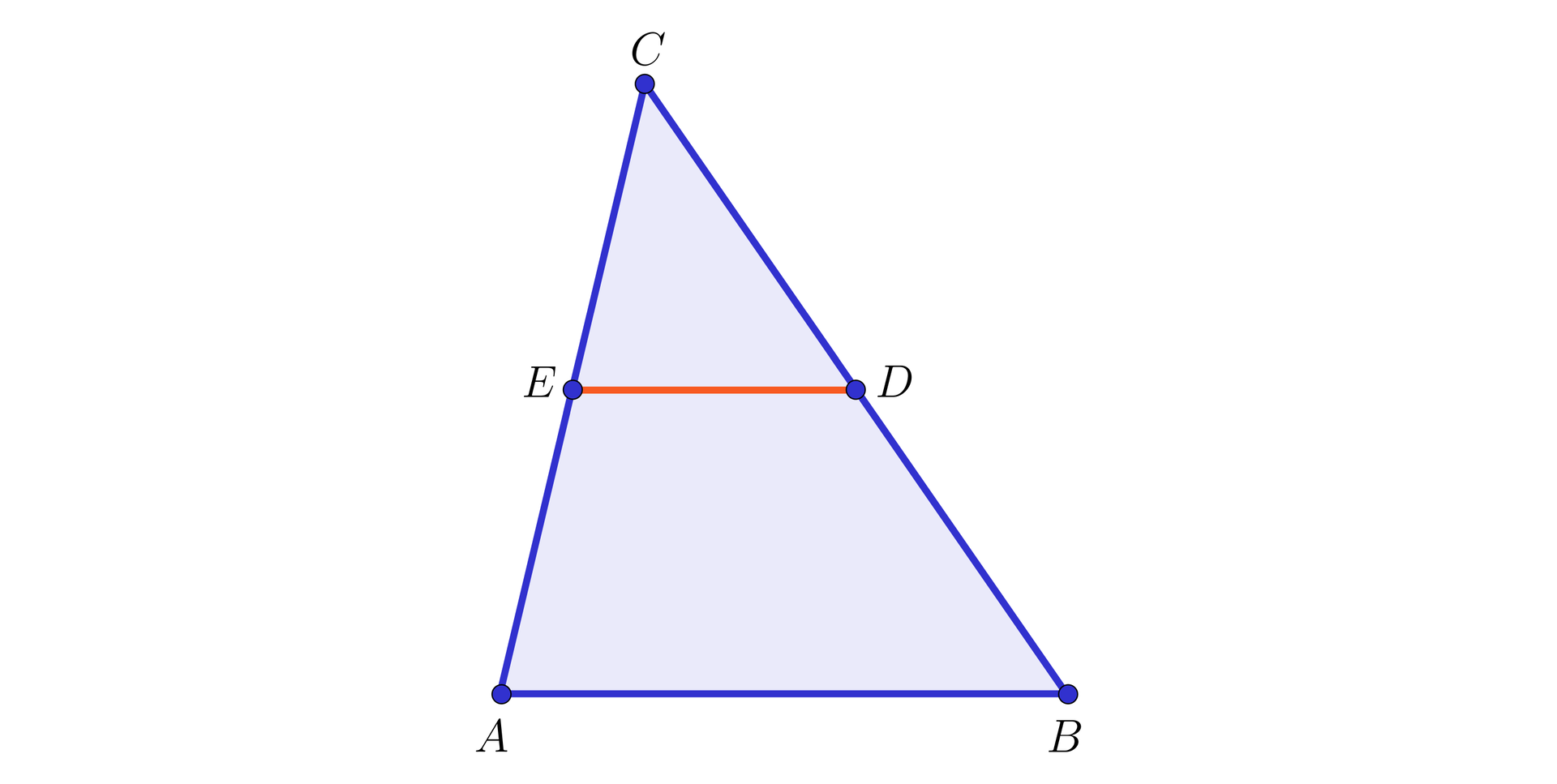
Zachodzi więc także cecha podobieństwapodobieństwa bbb i w konsekwencji: , czyli odcinek jest dwa razy dłuższy od odcinka .
Ponadto odcinek jest też równoległy do odcinka , ponieważ z cechy kkk wynika, że pary kątów odpowiadających (na rysunku poniżej zostały zaznaczone tym samym kolorem) są równe.
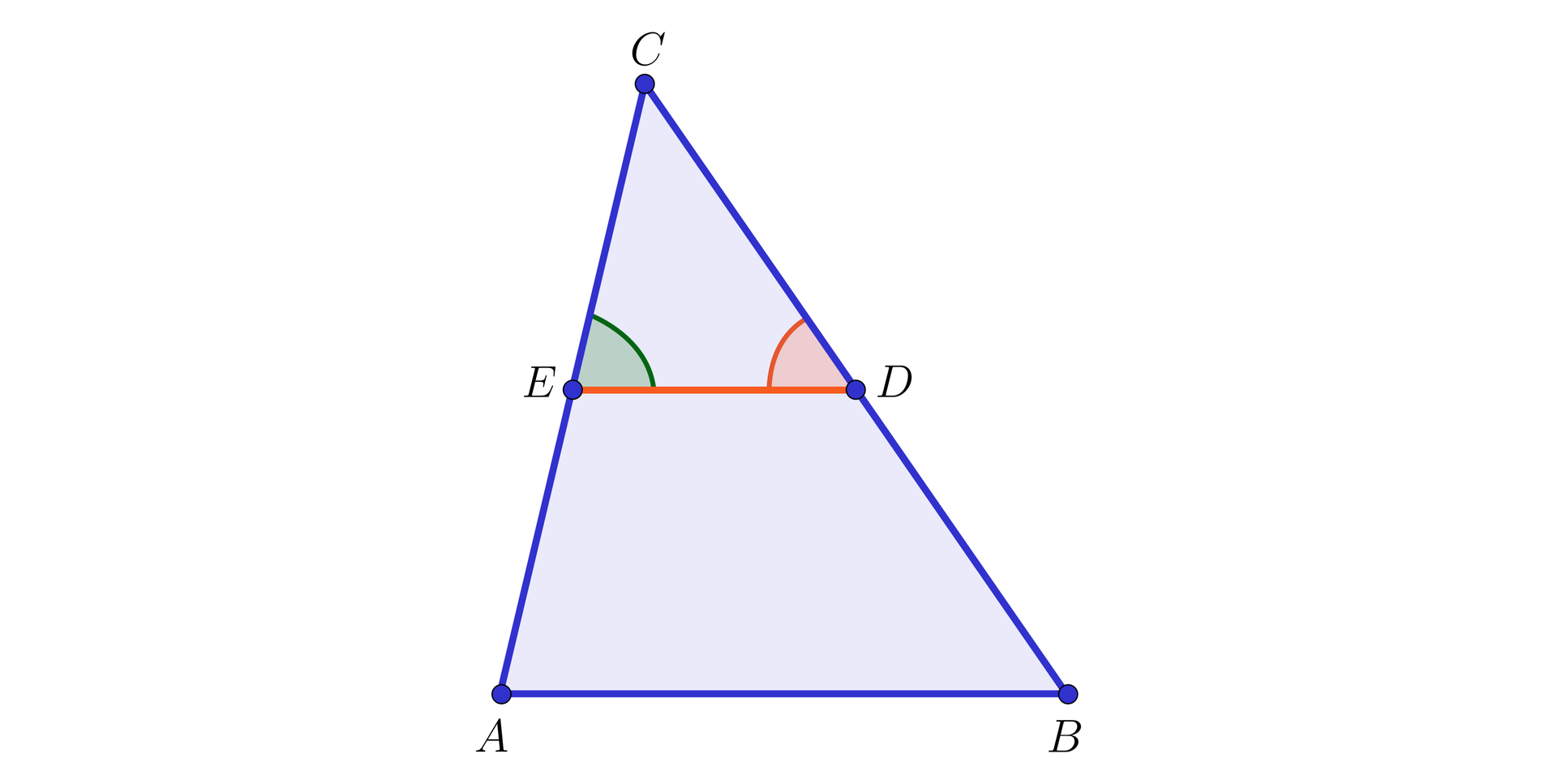
Otrzymujemy zatem poniższe twierdzenie.
Odcinek łączący środki dwóch boków w trójkącie jest równoległy do trzeciego boku i równy jego połowie .
Uwaga. Z twierdzenia o linii środkowej w trójkącieZ twierdzenia o linii środkowej w trójkącie wynika m. in. że środki boków dowolnego czworokąta są wierzchołkami równoległoboku (ten fakt bywa podawany jako twierdzenie Varignona).
Rozpatrzmy czworokąt , a środki jego kolejnych boków oznaczmy przez , , , (jak na poniższym rysunku).
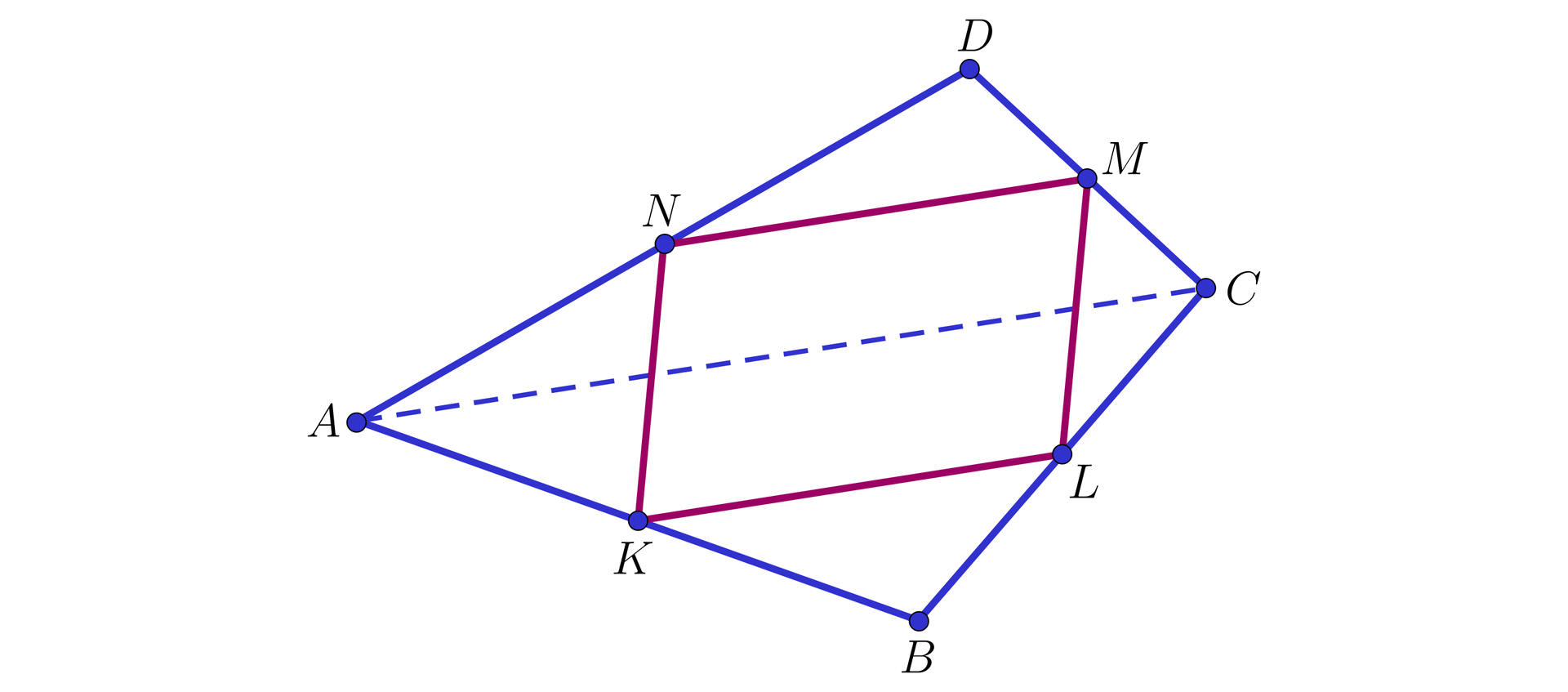
Dla dowodu wystarczy zauważyć, że:
odcinek to linia środkowa w trójkącie , skąd wynika, że oraz ,
odcinek to linia środkowa w trójkącie , skąd wynika, że oraz .
Wobec tego i , co oznacza, że czworokąt jest równoległobokiem. Koniec dowodu.
W przypadku szczególnych czworokątów dostajemy np., że:
środki boków dowolnego rombu są wierzchołkami prostokąta (co wynika stąd, że w rombie przekątne są prostopadłe),
środki boków dowolnego prostokąta są wierzchołkami rombu (co wynika stąd, że w prostokącie przekątne są równe),
środki boków trapezu równoramiennego są wierzchołkami rombu (co wynika stąd, że w trapezie równoramiennym przekątne są równe).
W trapezie poprowadzono przekątną i zaznaczono na niej punkt , dzielący ją na połowę. Następnie punkt połączono ze środkami boków i (jak na rysunku poniżej).

Stosując twierdzenie o linii środkowejtwierdzenie o linii środkowej w trójkątach i otrzymujemy, że:
oraz ,
oraz .
Zatem punkty , i leżą na jednej prostej, równoległej do obu podstaw trapezu, a więc
,
czyli odcinek jest równy połowie sumy odcinków i .
Zachodzi więc poniższe twierdzenie.
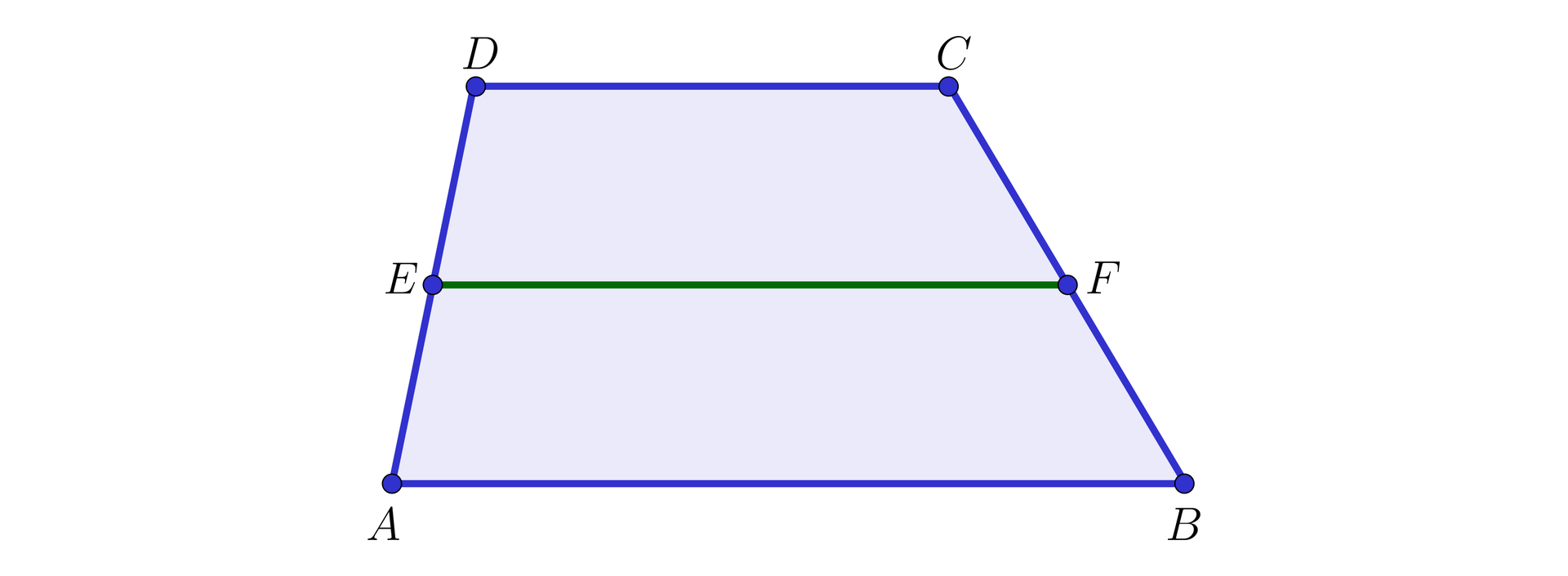
Odcinek łączący środki ramion trapezu jest równoległy do obu podstaw, a jego długość jest równa średniej arytmetycznej długości tych podstaw.
Jeżeli w trapezie , w którym , punkty oraz są środkami przekątnych - odpowiednio - i (jak na rysunku poniżej), to stosując twierdzenie o linii środkowej w trójkącietwierdzenie o linii środkowej w trójkącie otrzymujemy, że i .
Wykorzystując nastąpnie spostrzeżenia zapisane w poprzednim przykładzie dostajemy, że punkt leży na linii środkowej trójkąta , a więc
.

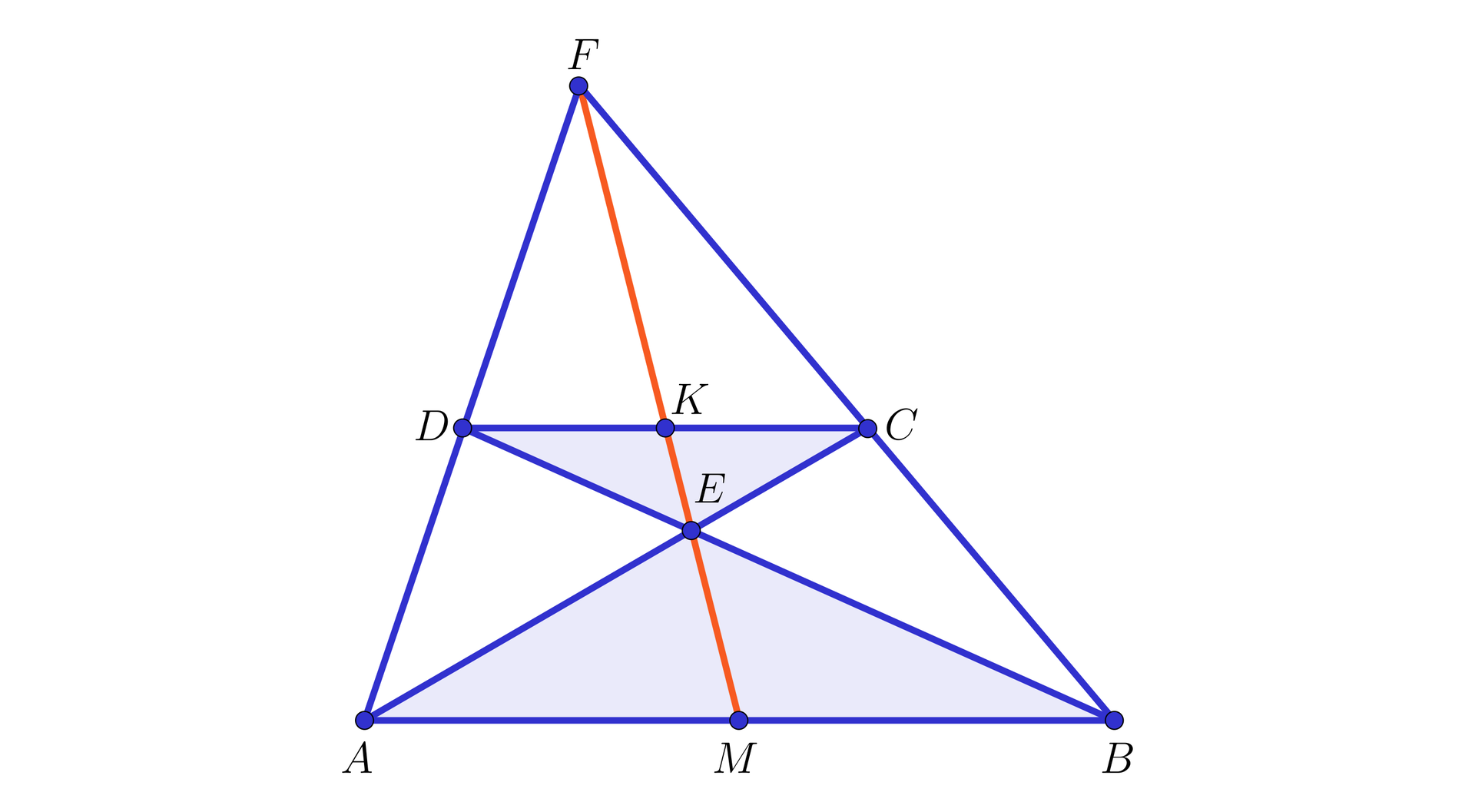
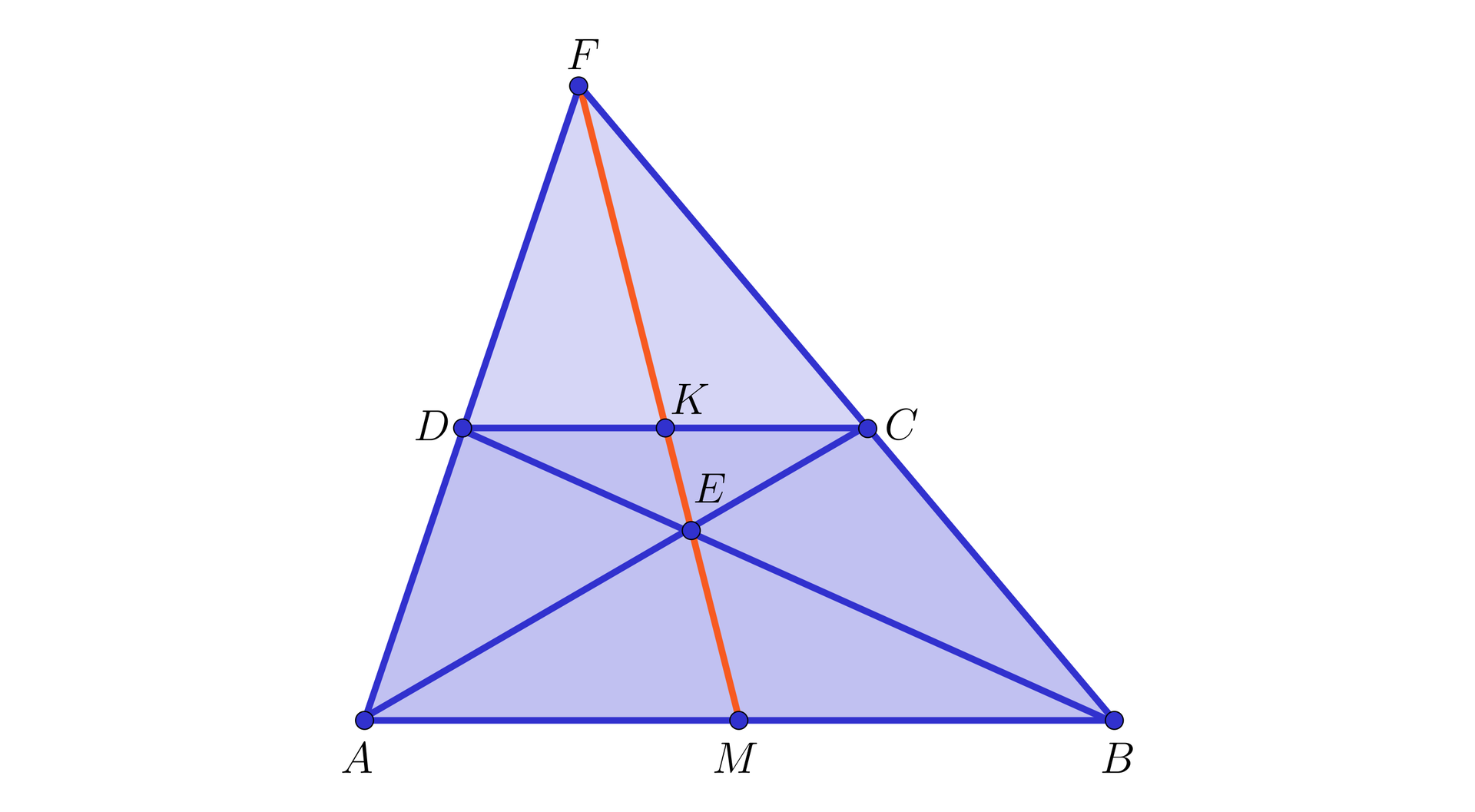
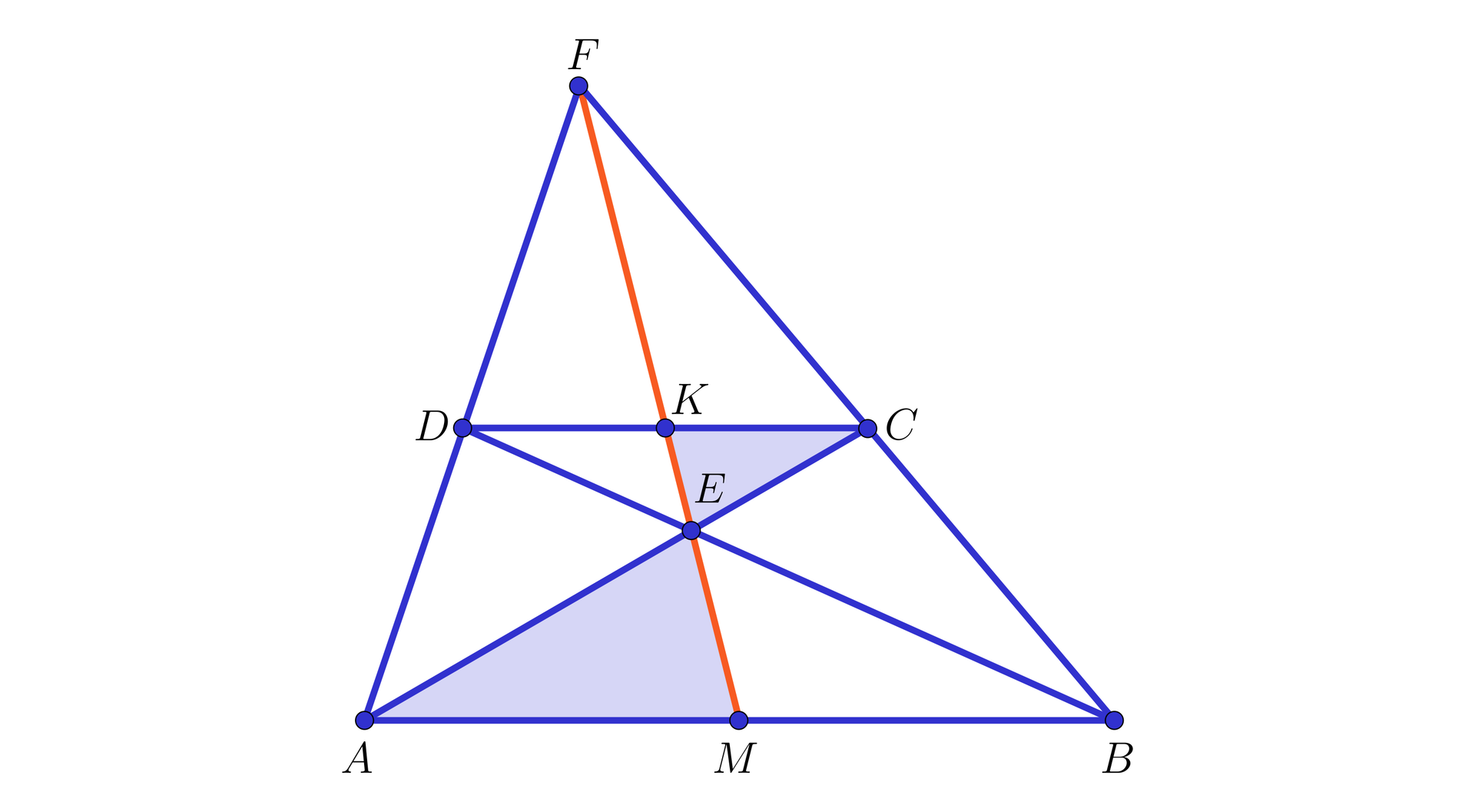
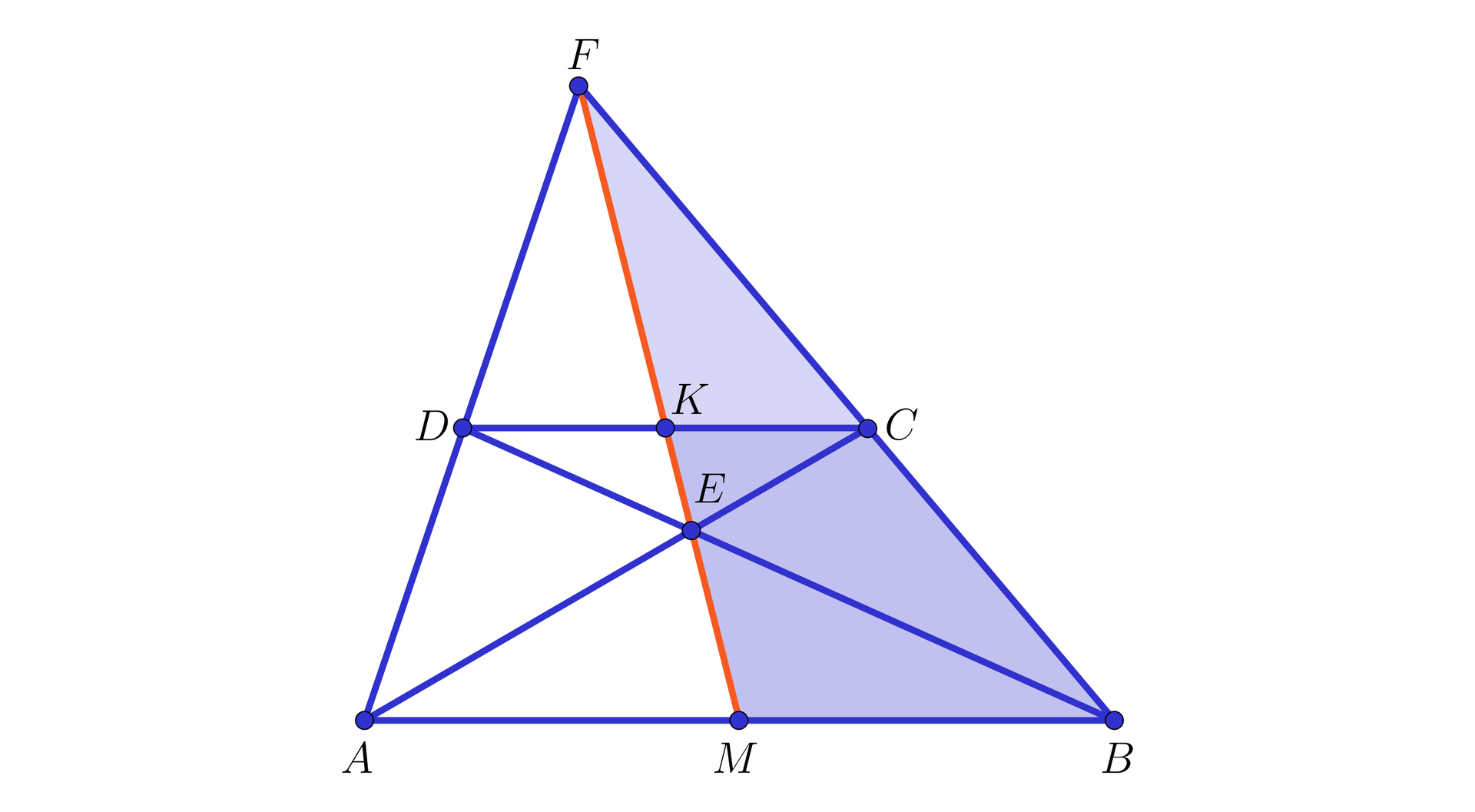
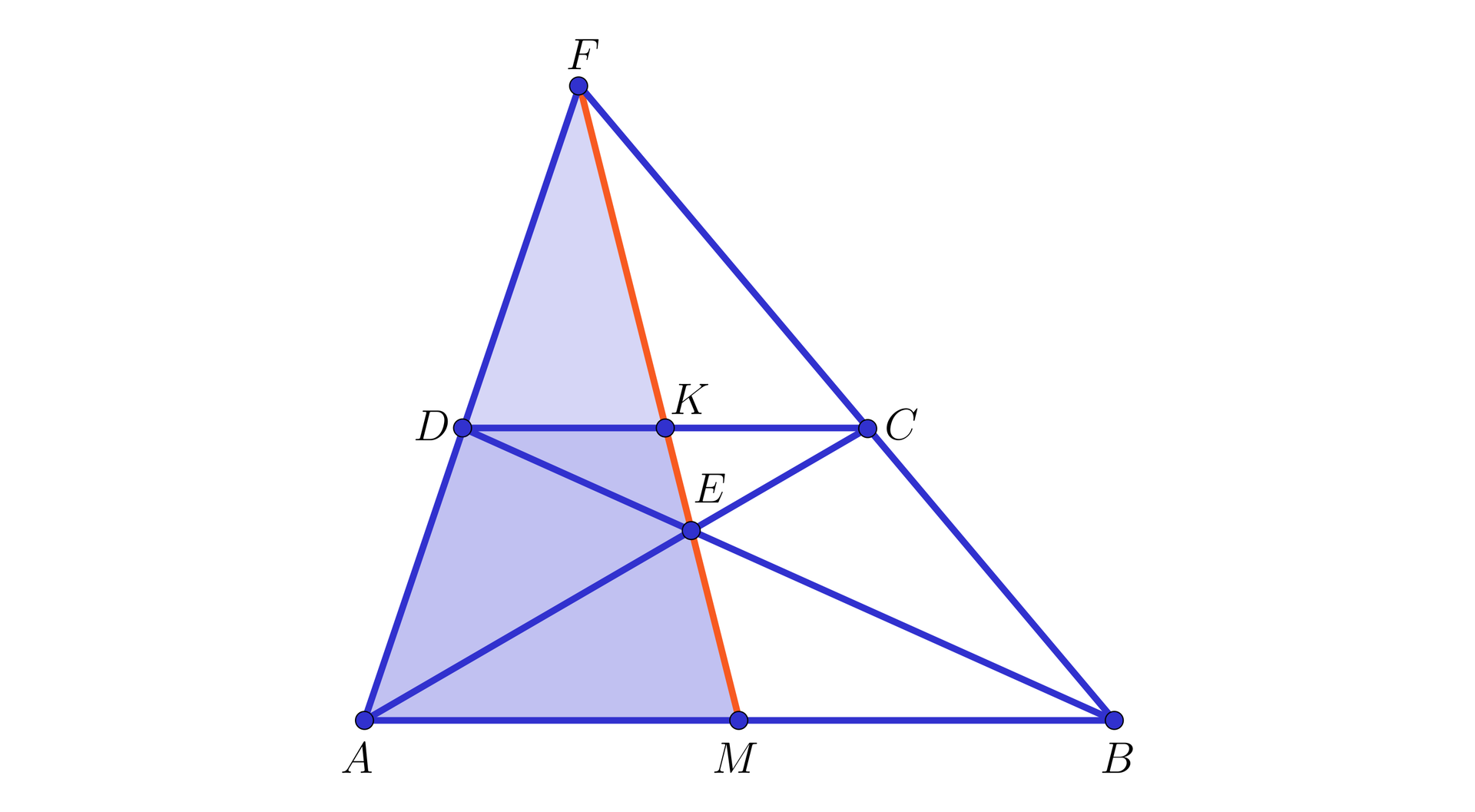
W trójkącie poprowadzono środkowe i , które przecięły się w punkcie .
Wykażemy, że oraz .
Z własności linii środkowejlinii środkowej w trójkącie wynika, że .
Zatem równe są pary kątów naprzemianległych: i oraz i (zobacz rysunek poniżej).
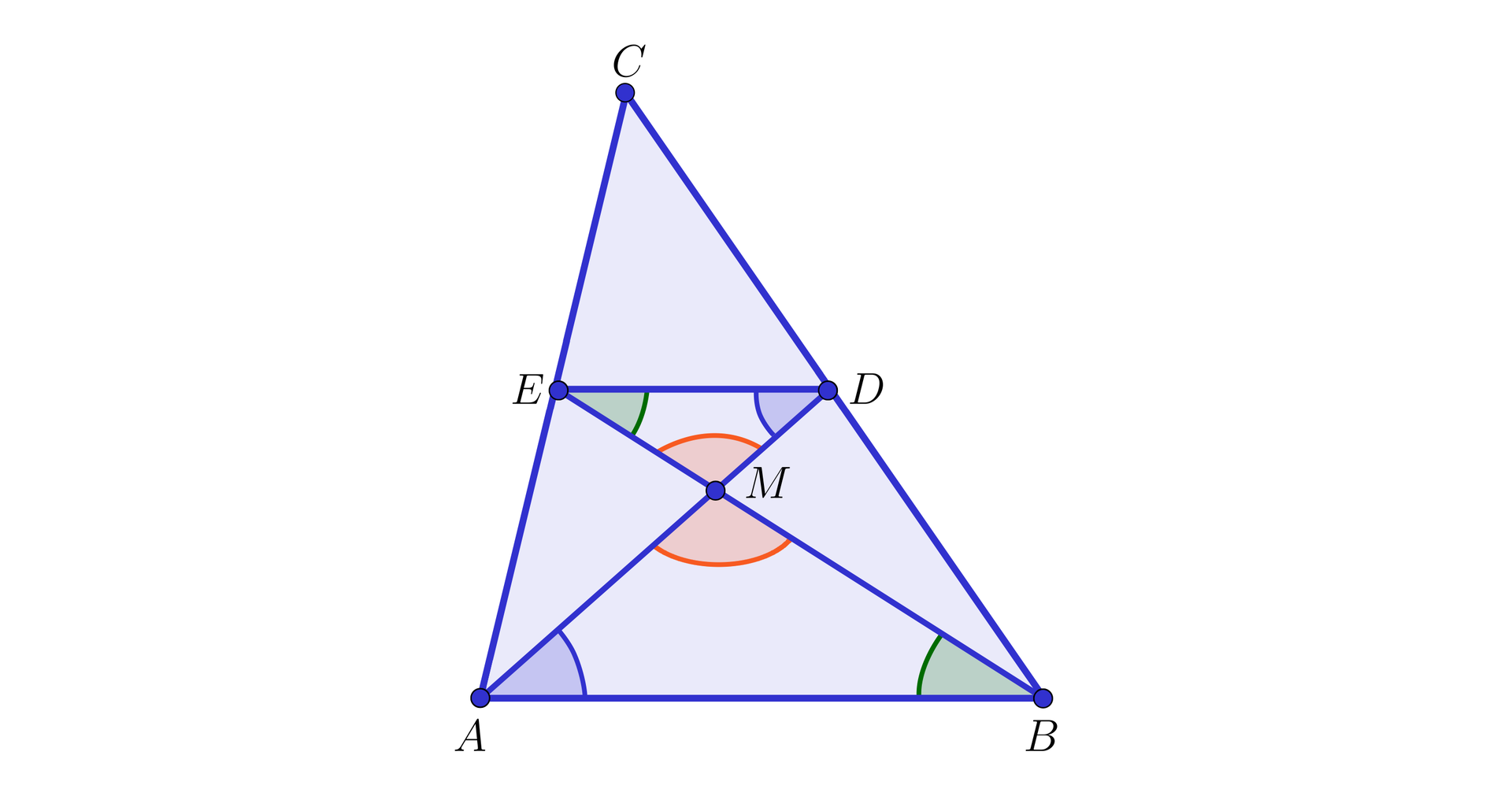
Oznacza to, że trójkąty i są podobnepodobne na mocy cechy kkk.
Ponieważ , więc skala podobieństwaskala podobieństwa tych trójkątów jest równa , skąd dostajemy, że oraz .
Możemy więc zapisać, że środkowe i przecinają się w takim punkcie , który dzieli każdą z nich w stosunku (licząc od wierzchołka).
Rozpatrując inną parę środkowych, np. i oraz rozumując podobnie, jak w przypadku pary środkowych i , otrzymamy wniosek, że środkowe i przecinają się w punkcie, który dzieli każdą z nich w stosunku (licząc od wierzchołka). Ponieważ jest punktem, który dzieli środkową w stosunku , licząc od wierzchołka, co oznacza, że jest to punkt, który leży również na środkowej .
Udowodniliśmy w ten sposób poniższe twierdzenie.
Środkowe w dowolnym trójkącie przecinają się w jednym punkcie, który dzieli każdą z nich w stosunku (licząc od wierzchołka).
Punkt, w którym przecinają sie środkowe trójkąta jest zwyczajowo nazywany środkiem ciężkości tego trójkąta.
Rozpatrzmy trapez, który nie jest równoległobokiem a w nim prostą, która przechodzi przez punkt przecięcia przekątnych i punkt przecięcia prostych zawierających nierównoległe boki.
Wykażemy, że ta prosta dzieli każdą z podstaw trapezu na połowy.
Dowód. Przyjmijmy, że podstawami trapezu są odcinki oraz i załóżmy, że .
Oznaczmy też (jak na poniższym rysunku):
przez – punkt przecięcia przekątnych i trapezu,
przez – punkt przecięcia prostych i ,
przez – punkt, w którym prosta przecina podstawę ,
przez – punkt, w którym prosta przecina podstawę .
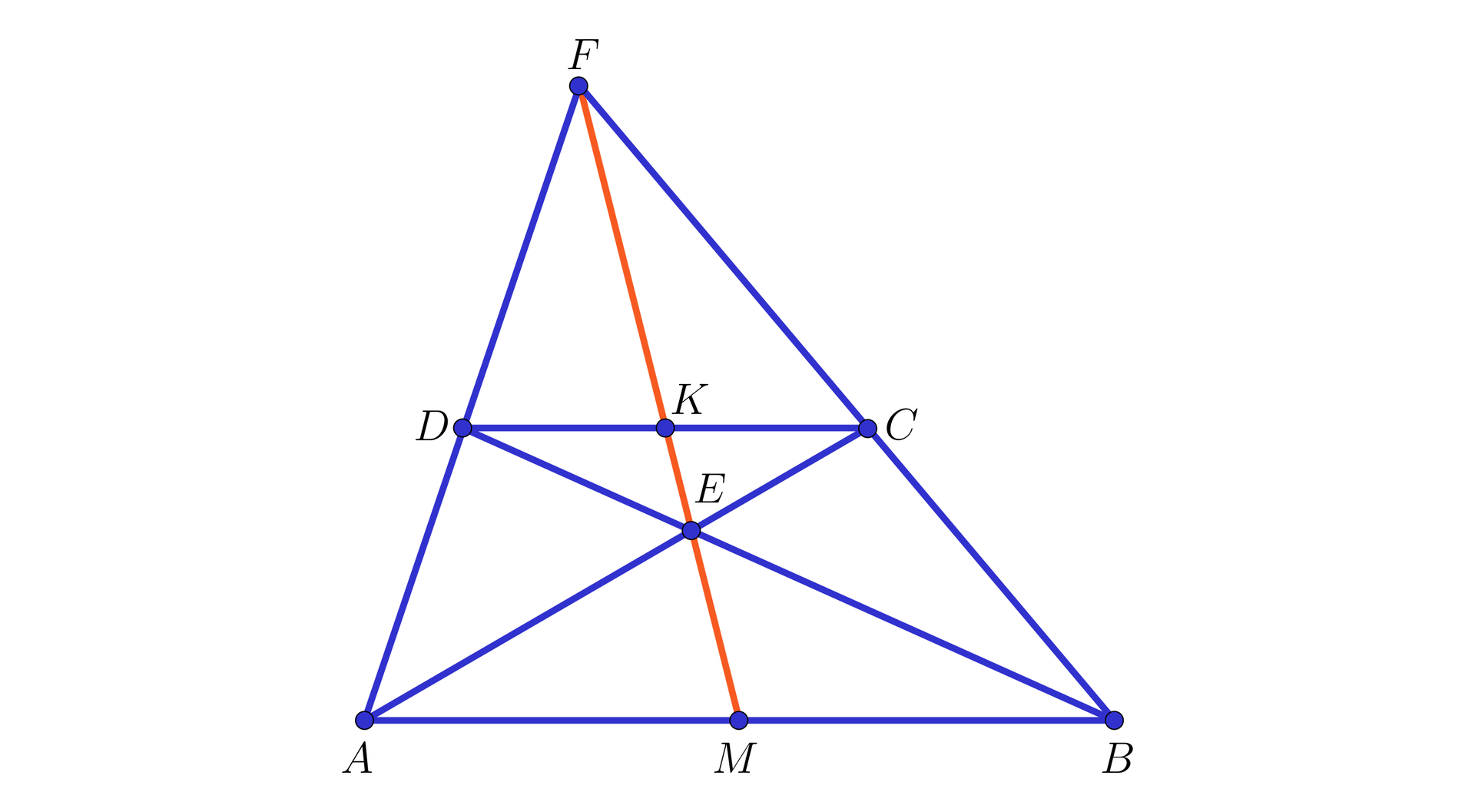
Znajdziemy teraz pary trójkątów podobnychtrójkątów podobnych i zapiszemy przydatne dla dowodu zależności między długościami ich boków.
W każdym z poniższych sześciu przypadków korzystamy z cechy kkk, wiedząc, że:
proste i są równoległe,
punkty , , , są współliniowe,
punkty , , są współliniowe,
punkty , , są współliniowe,
Oto te przypadki.
(1) (zobacz rysunek),
skąd wynika, że .
(2) (zobacz rysunek),
skąd wynika, że .
(3) (zobacz rysunek).
Wynika stąd, że
(4) (zobacz rysunek).

Wynika stąd, że
(5) (zobacz rysunek).
Wynika stąd, że ,
(6) (zobacz rysunek).
Wynika stąd, że .
Wykorzystując otrzymane zależności, udowodnimy na kilka sposobów tezę postawioną w zadaniu.
Z zależności (3), (1), (2) i (6) otrzymujemy:
, czyli , skąd wynika, że jest środkiem podstawy .
Z zależności (4), (1), (2) i (6) otrzymujemy:
, czyli , skąd wynika, że jest środkiem podstawy .
Z zależności (3), (1), (2) i (5) otrzymujemy:
, czyli , skąd wynika, że jest środkiem podstawy .
Z zależności (4), (1), (2) i (5) otrzymujemy:
, czyli , skąd wynika, że jest środkiem podstawy .
Z zależności (3) i (1) oraz (5) i (2) dostajemy kolejno:
, czyli ,
, czyli .
Wobec tego
.
Oznacza to, że jest środkiem boku .
Korzystając z zależności zapisanej wyżej (jako wniosek z (5) i (2)) otrzymujemy równość
, skąd .
Wobec tego jest środkiem boku .
W ten sposób dowód uznajemy za zakończony.
W kolejnych przykładach pokażemy, jak wykorzystać podobieństwo trójkątów w zadaniach obliczeniowych.
W trójkącie punkt jest środkiem boku , symetralna tego boku przecina bok w punkcie i przedłużenie boku w punkcie (jak na poniższym rysunku).
Wysokość jest równa , a punkt dzieli bok tak, że .
Obliczymy długość odcinka .
Rozwiązanie
Przyjmijmy, że , gdzie .
Wtedy z warunków zadania otrzymujemy, że , oraz .
Zauważmy, że:
ponieważ proste i są prostopadłe do prostej , więc trójkąty i są prostokątne i mają wspólny kąt przy wierzchołku . Zatem na mocy cechy kkk są to trójkąty podobnepodobne, a to oznacza, że , skąd ;
ponieważ proste i są prostopadłe do prostej , więc trójkąty i są prostokątne i mają wspólny kąt przy wierzchołku . Zatem na mocy cechy kkk są to trójkąty podobnepodobne, a to oznacza, że , skąd .
Wynika stąd, że .
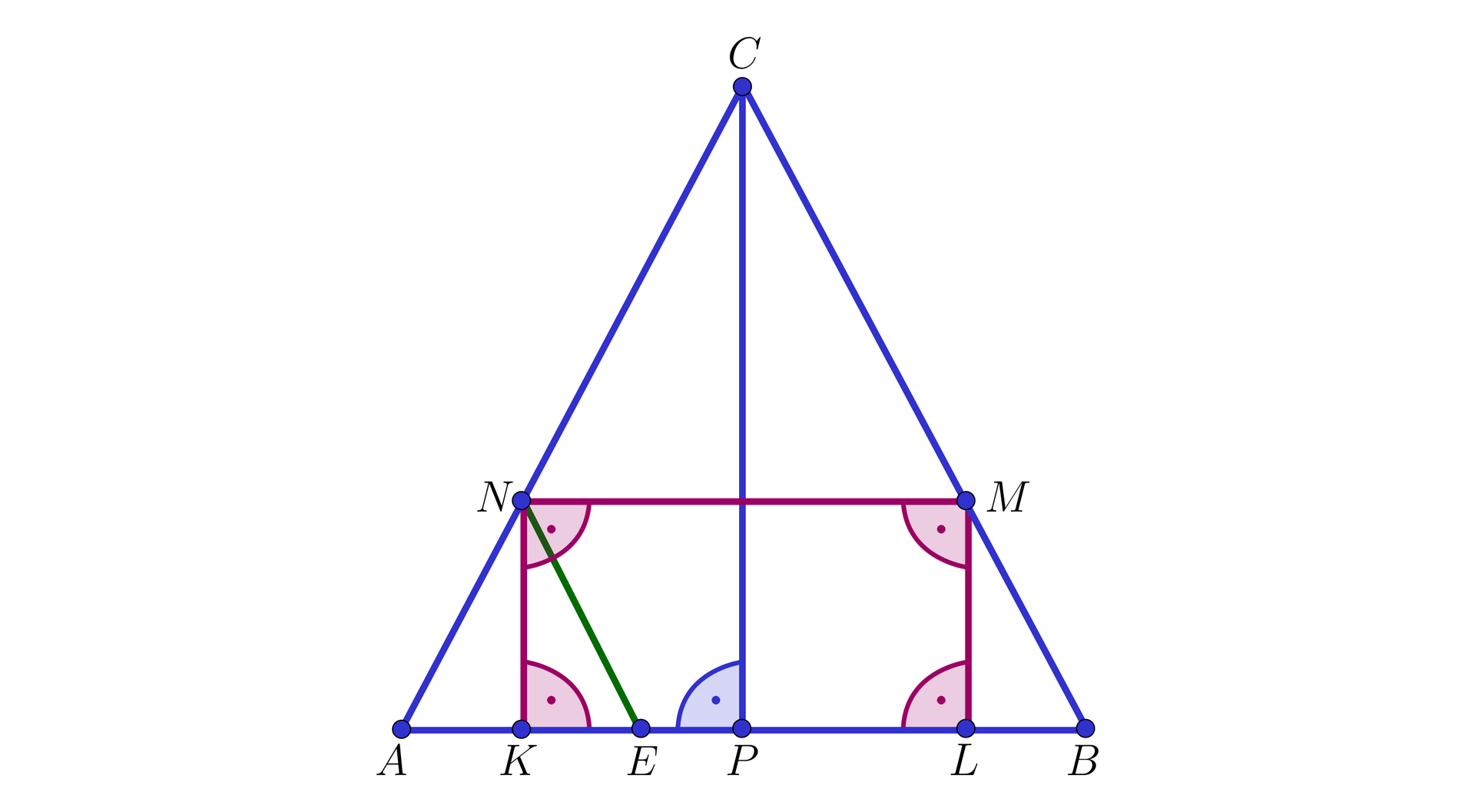
a) W trójkąt prostokątny o przyprostokątnych i wpisano prostokąt , w którym oraz , i (jak na poniższym rysunku).
Obliczymy długości boków tego prostokąta.
Rozwiązanie
Przyjmujemy, że . Wtedy z warunków zadania otrzymujemy:
, , oraz .
Zauważmy, że trójkąty i są prostokątne oraz mają wspólny kąt przy wierzchołku , więc są podobnepodobne na podstawie cechy kkk.
Zachodzi więc równość , skąd otrzymujemy .
Wobec tego
czyli .
Oznacza to, że boki prostokąta mają długości:
oraz .
b) W trójkąt równoramienny o podstawie i ramionach wpisano prostokąt , w którym oraz , i (jak na poniższym rysunku).

Obliczymy długości boków tego prostokąta.
Rozwiązanie
Przyjmujemy, że . Wtedy z warunków zadania otrzymujemy .
Oznaczmy przez środek boku .
Ponieważ trójkąt jest równoramienny, więc symetralna podstawy zawiera wysokość poprowadzoną z wierzchołka . Oznacza to, że .
Wobec tego:
,
w trójkącie z twierdzenia Pitagorasa otrzymujemy zależność , skąd obliczamy, że .
Dalszą część rozwiązania przeprowadzimy dwoma sposobami.
sposób. Oznaczmy przez taki punkt, że czworokąt jest równoległobokiem. Stąd i .
Ponieważ:
z własności trójkąta
A B C ∢ C A B = ∢ C B A ∢ N A E = ∢ N E A z własności prostokąta
K L M N M N ∥ A B E ∈ A B
Oznacza to, że:
trójkąt
A E N A E = A B - E B = 32 - 2 x K A E A K = K E = 1 2 E B = 1 2 32 - 2 x = 16 - x K N ⊥ A E
Wobec tego trójkąty
Otrzymujemy stąd zależność
Wynika stąd, że boki prostokąta
trójkąt
N M C N M ⊥ C P środek
Q N M C P K P = P L = N Q = Q M = x
Stąd czworokąty

Zauważmy, że trójkąty
Zachodzi więc równość
Oznacza to, że
czyli
Wobec tego boki prostokąta
W równoległoboku
Odcinki
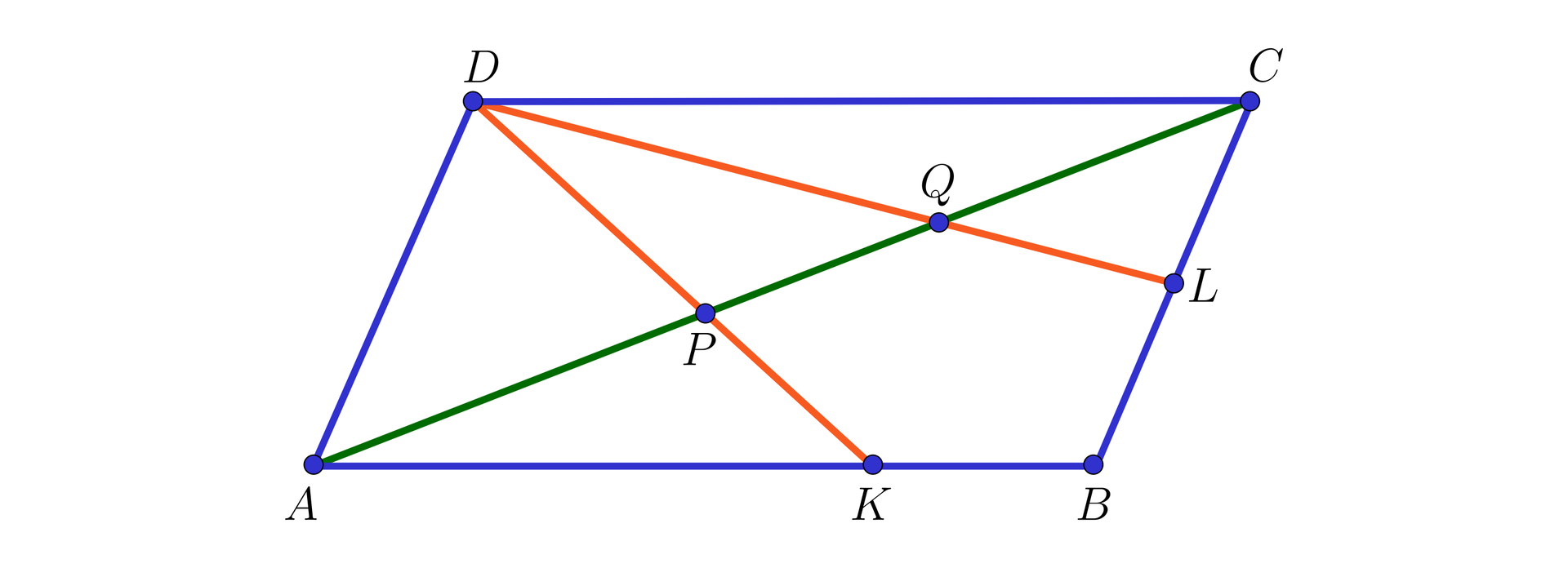
Obliczymy
Rozwiązanie
Przyjmijmy, że
Wtedy z warunków zadania otrzymujemy, że
Zauważmy, że:
(1) ponieważ proste
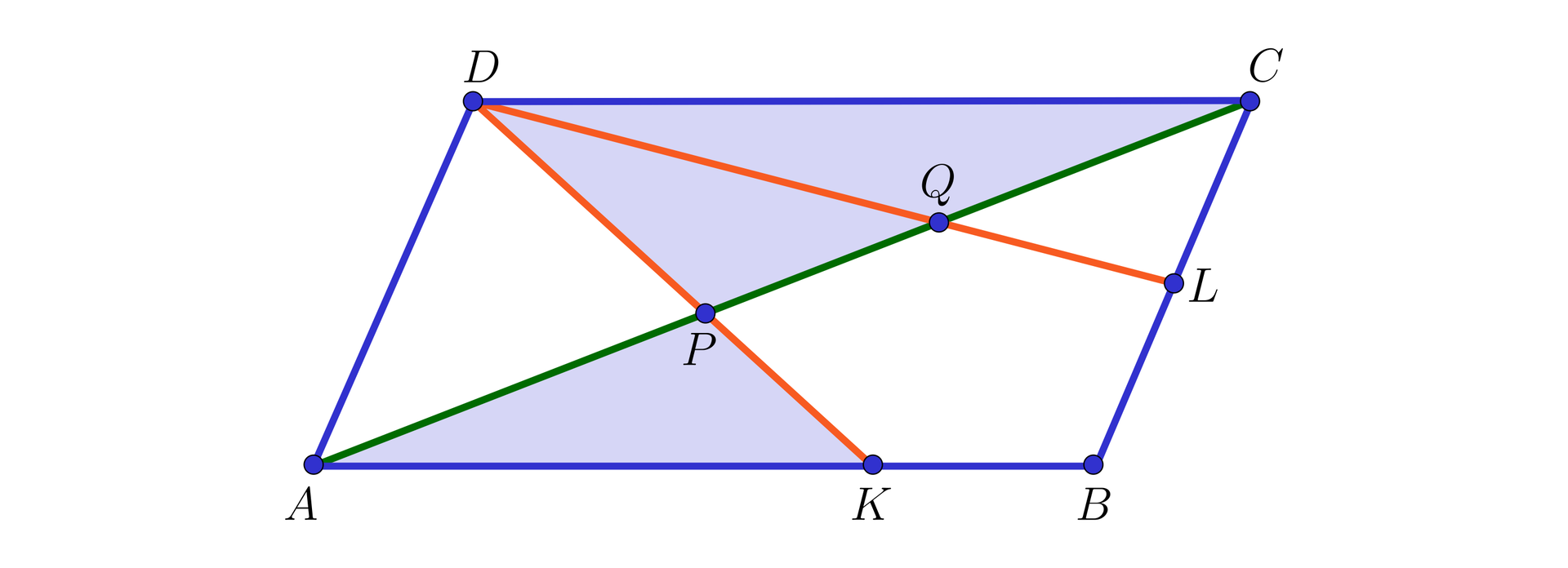
Stąd
Zatem
(2) ponieważ proste

Stąd
Zatem
Wynika stąd, że
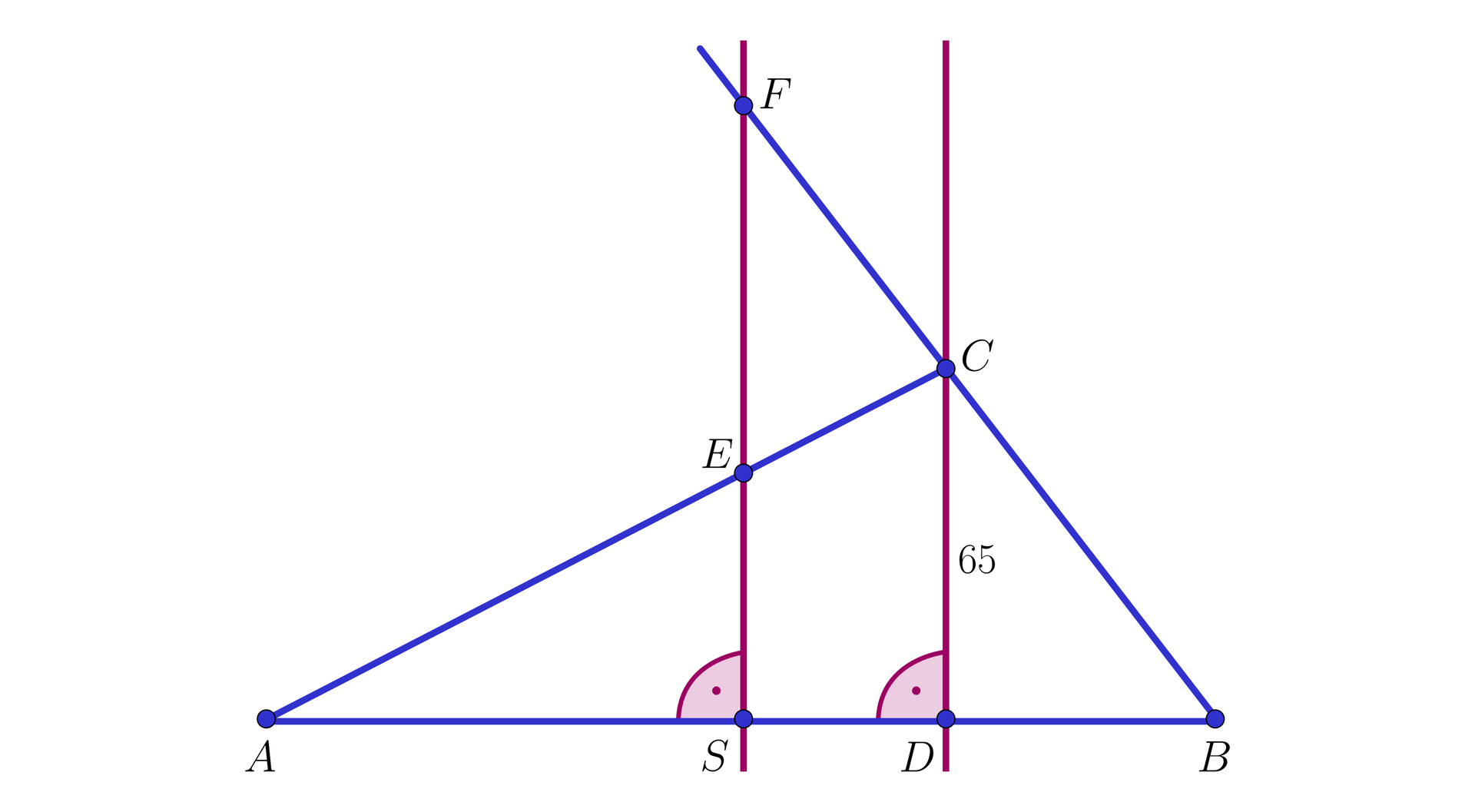
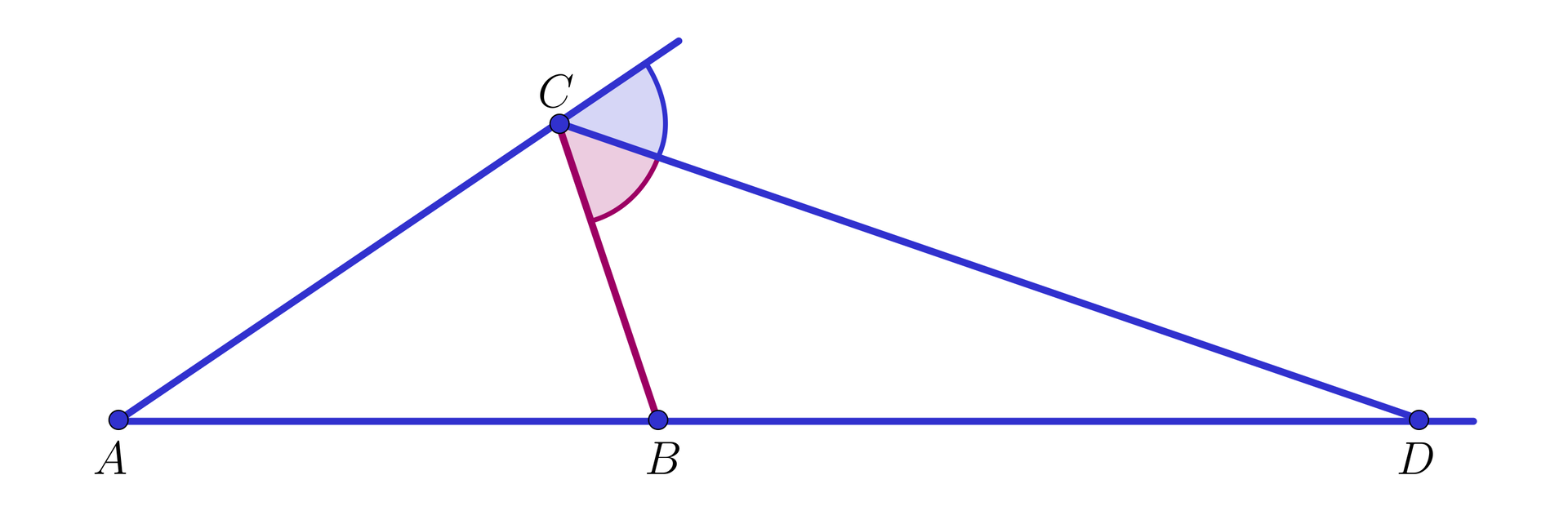
W trójkącie
Obliczymy długość odcinka dwusiecznej kąta
Rozwiązanie
Oznaczmy przez
Z treści zadania otrzymujemy, że
Poprowadźmy przez punkt
równoległą do
B C E A C równoległą do
A C F B C
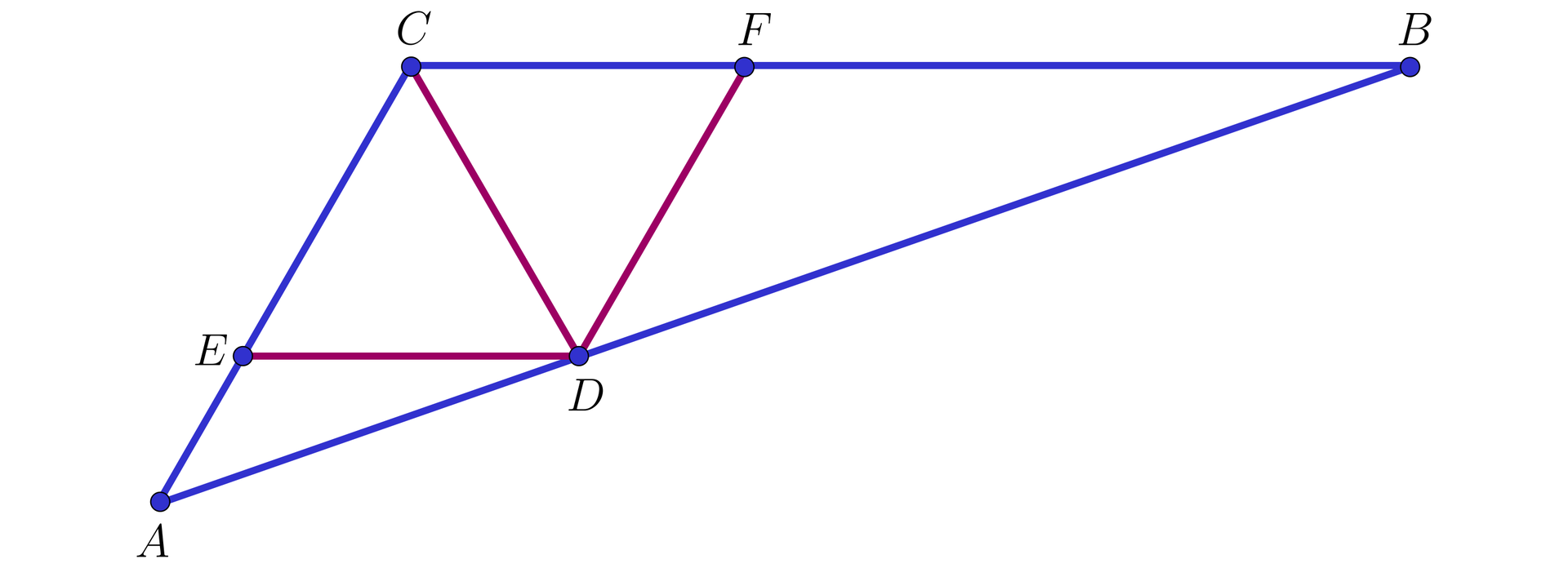
Zauważmy, że wtedy równe są dwie pary kątów naprzemianległych:
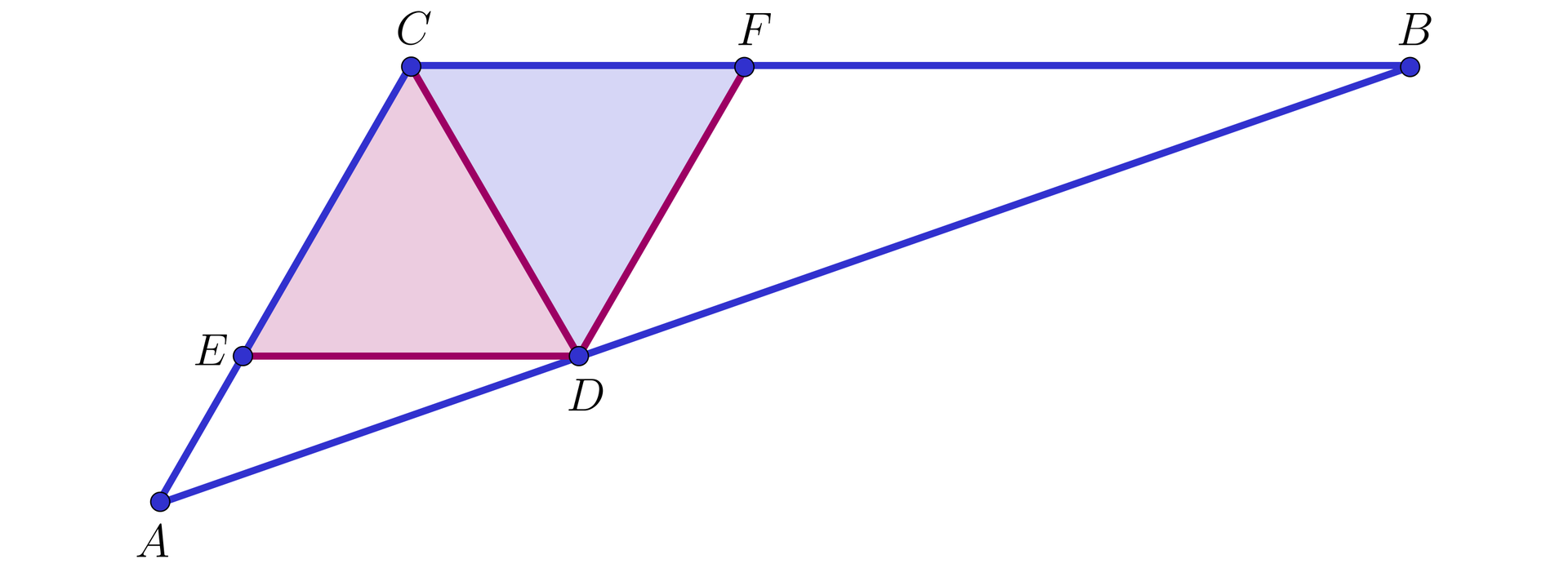
Oznaczmy szukaną długość odcinka
Wtedy
Zauważmy, że ponieważ proste
Wynika stąd, że prawdziwa jest równość
czyli
Oznacza to, że długość szukanego odcinka dwusiecznej kąta
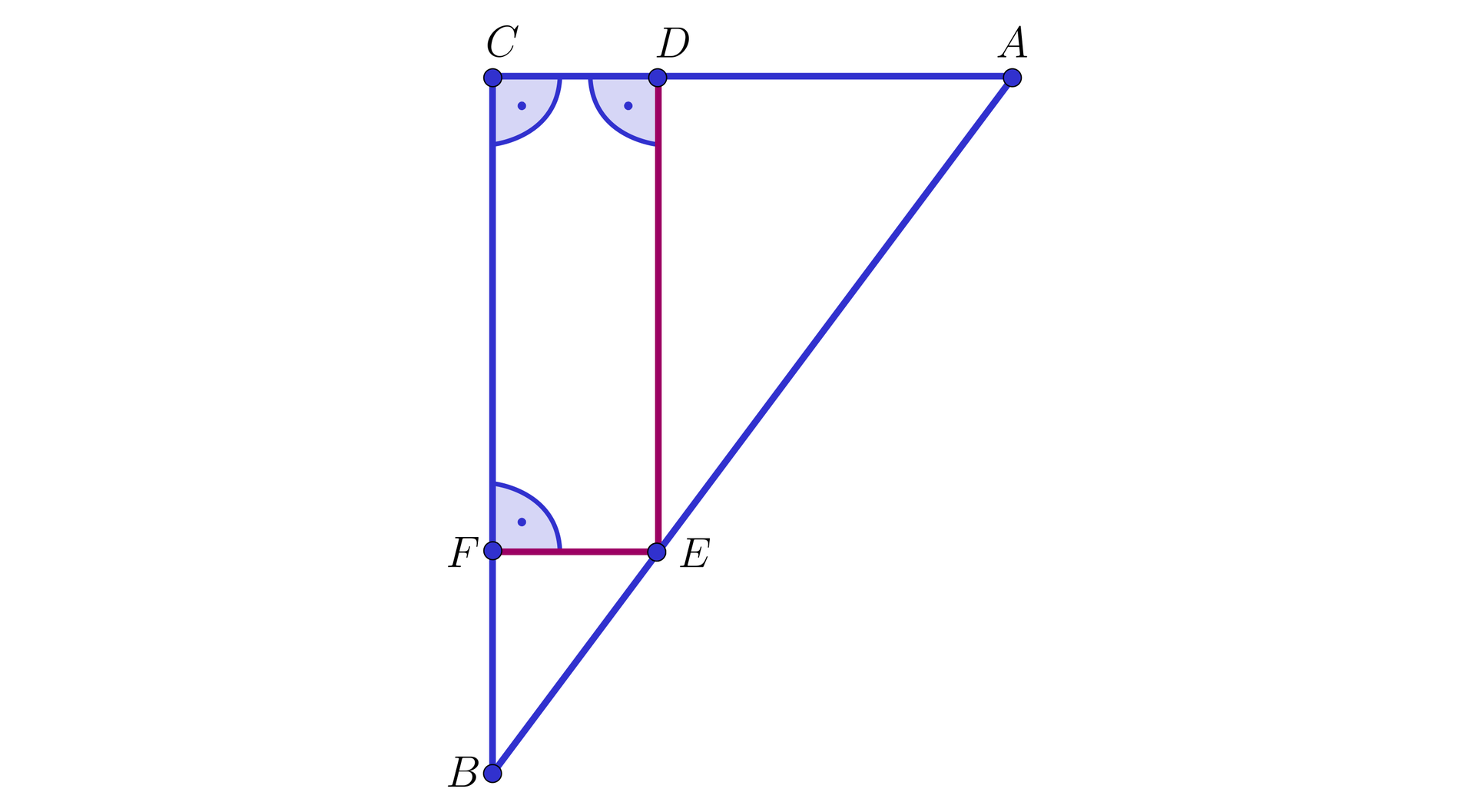
Uwaga. Do rozwiązania powyższego zadania z wykorzystaniem trójkątów podobnychpodobnych można też zastosować pomysł omówiony w poprzednim przykładzie. Wystarczy w tym celu wziąć pod uwagę taki punkt

Ponieważ
Ponadto, ponieważ proste
Wobec tego zachodzi równość
Zainteresowanym rozwijaniem swoich intuicji dotyczących wykorzystywania podobieństwa trójkątów polecamy jeszcze jeden pomysł na rozwiązanie rozpatrywanego zadania.
Weźmy mianowicie pod uwagę punkt
Nietrudno jest wtedy pokazać, że:
ten równoległobok jest rombem,
na jego przekątnej
C Q D trójkąty
C P Q B C Q

Pozostawiamy czytelnikowi zapisanie wynikających z powyższych spostrzeżeń takich zależności, które prowadzą do obliczenia szukanej długości .
Na zakończenie należy wspomnieć, że skuteczną metodą, która pozwala rozwiązać omawiane zadanie jest też zastosowanie wzoru na pole trójkąta z użyciem trygonometrii. Zapiszemy wtedy:
pole trójkąta
A B C P A B C = 1 2 · 2 · 4 · sin 120 ° = 2 3 pole trójkąta
A D C P A D C = 1 2 · 2 · C D · sin 60 ° = 3 2 C D pole trójkąta
B D C P B D C = 1 2 · 4 · C D · sin 60 ° = 3 C D
a ponieważ
skąd
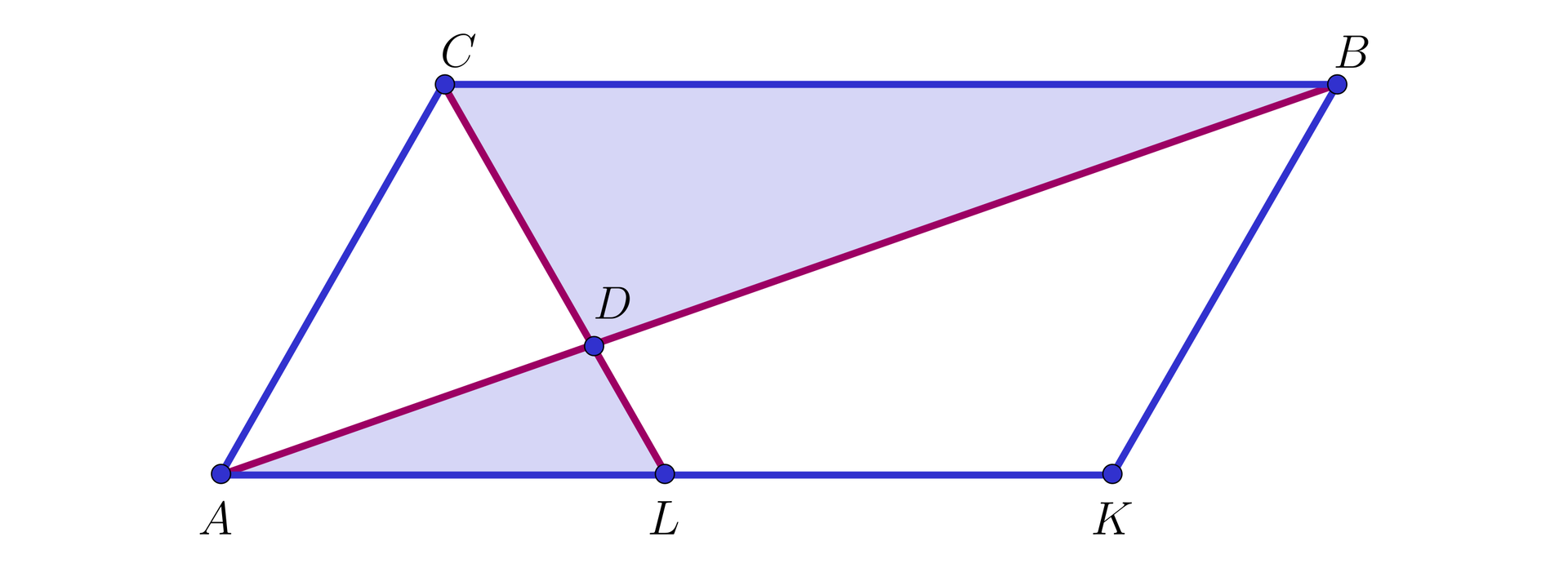
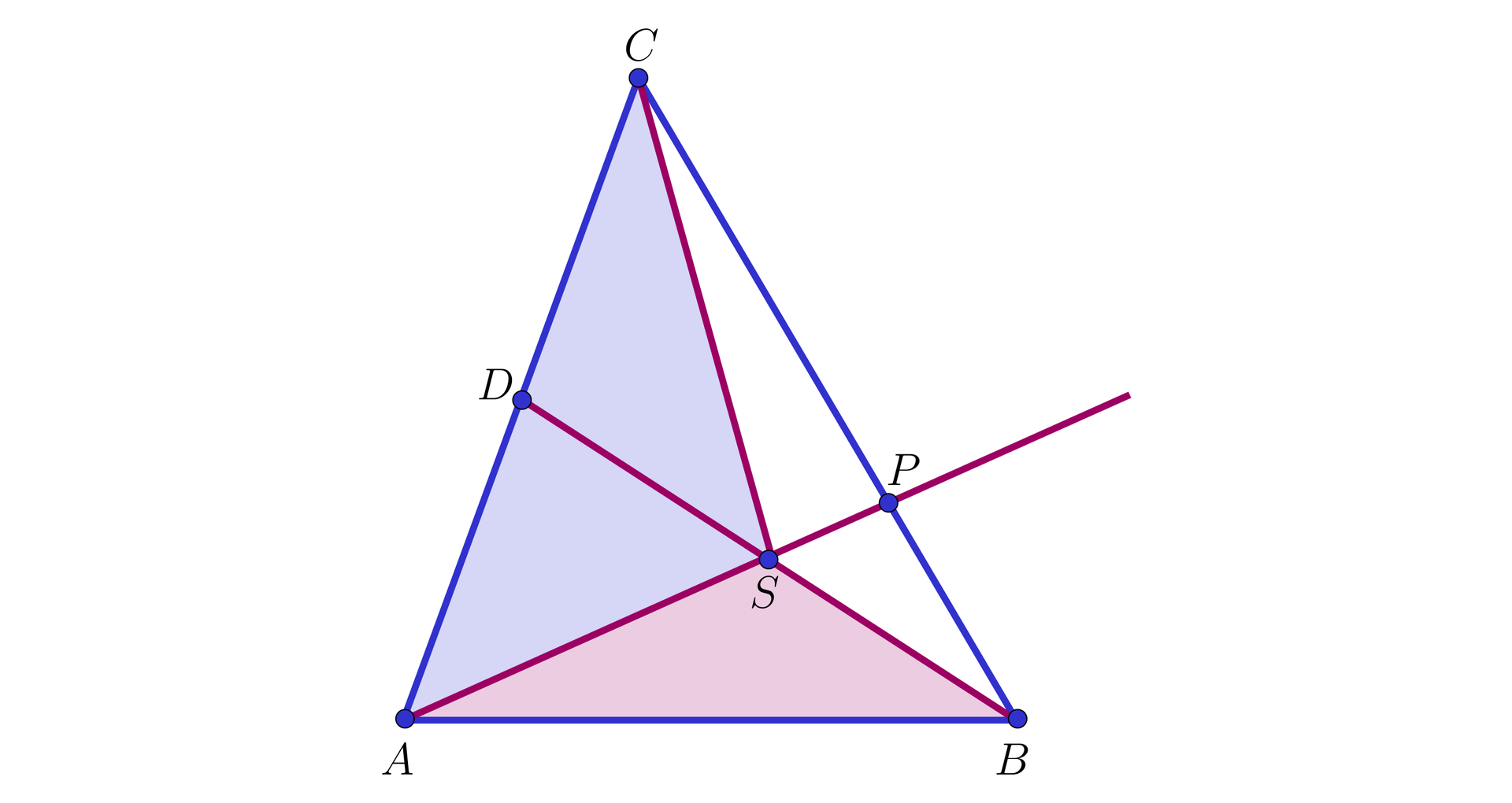
W trójkącie
Wykażemy, że
Rozwiązanie
I sposób. Rozpatrzmy trójkąt
Wówczas odcinek
Ponieważ
Wynika stąd, że
Ponieważ
Koniec dowodu.
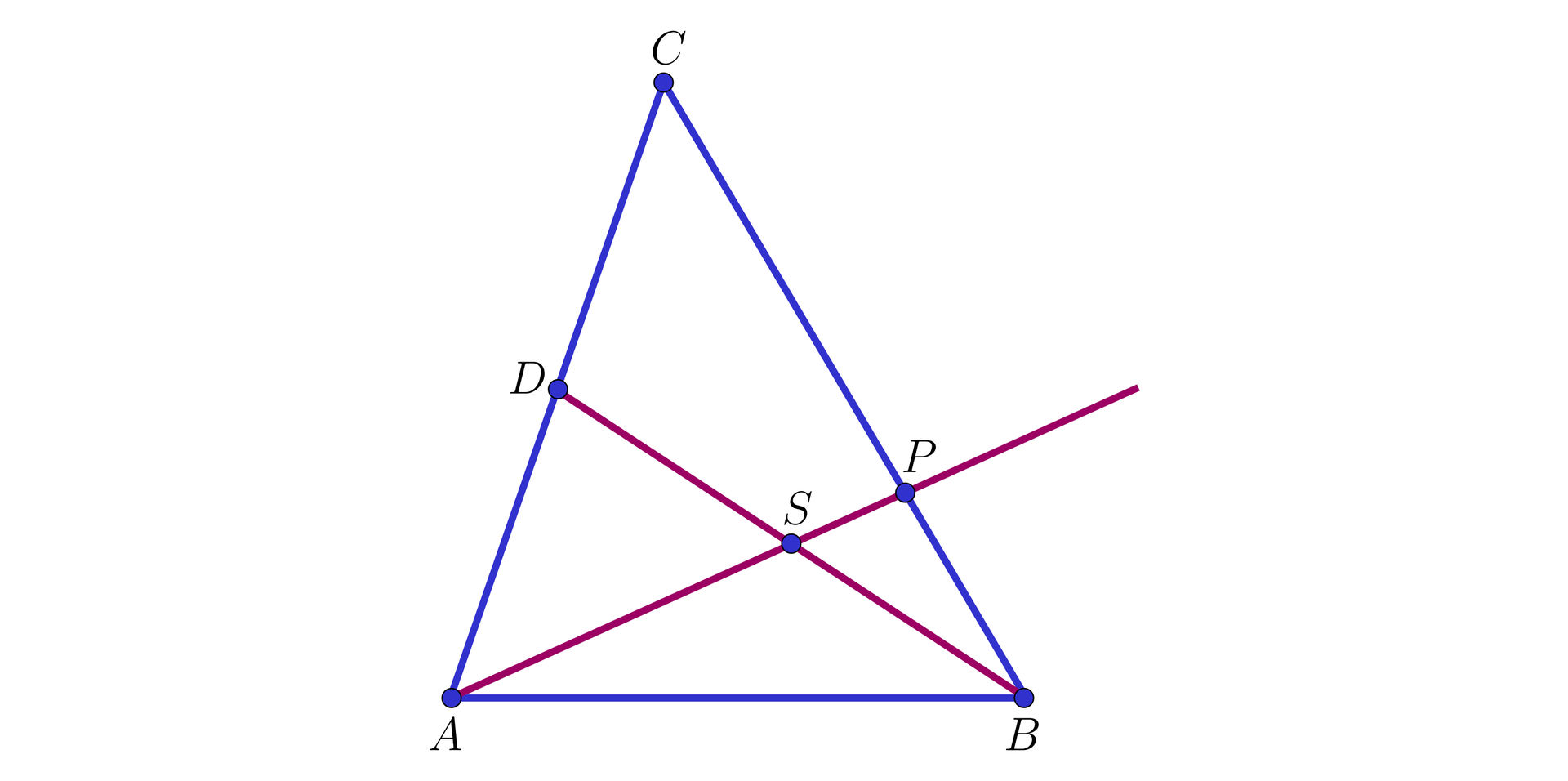
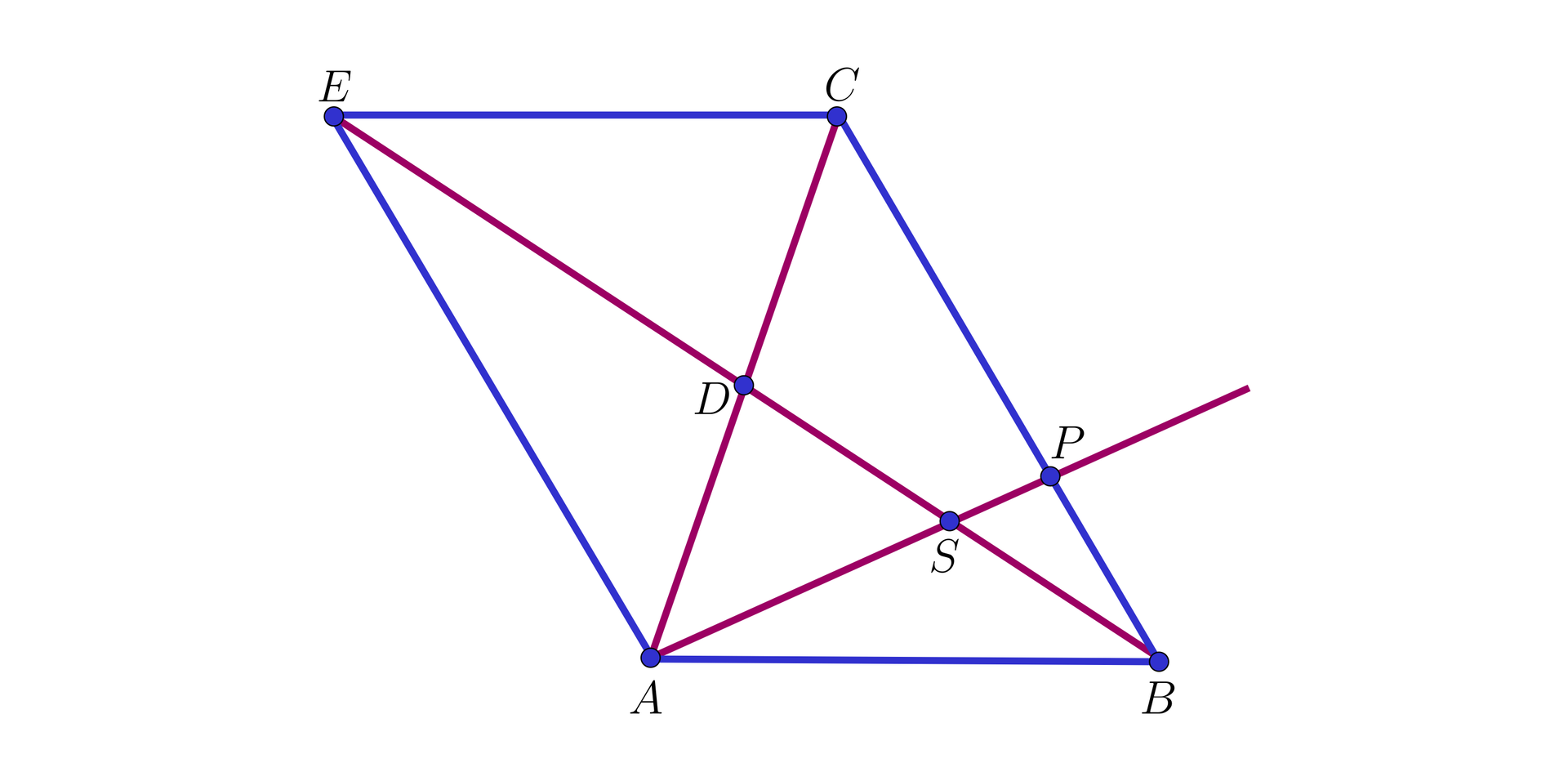
Uwaga. Jeżeli przez punkt
ta prosta przetnie ramię
C B A C B Q A D D C = P Q Q C C Q = P Q proste równoległe
D Q A P D B C B S S D = B P P Q B P = P Q
Otrzymane wnioski prowadzą bezpośrednio do tezy zadania.
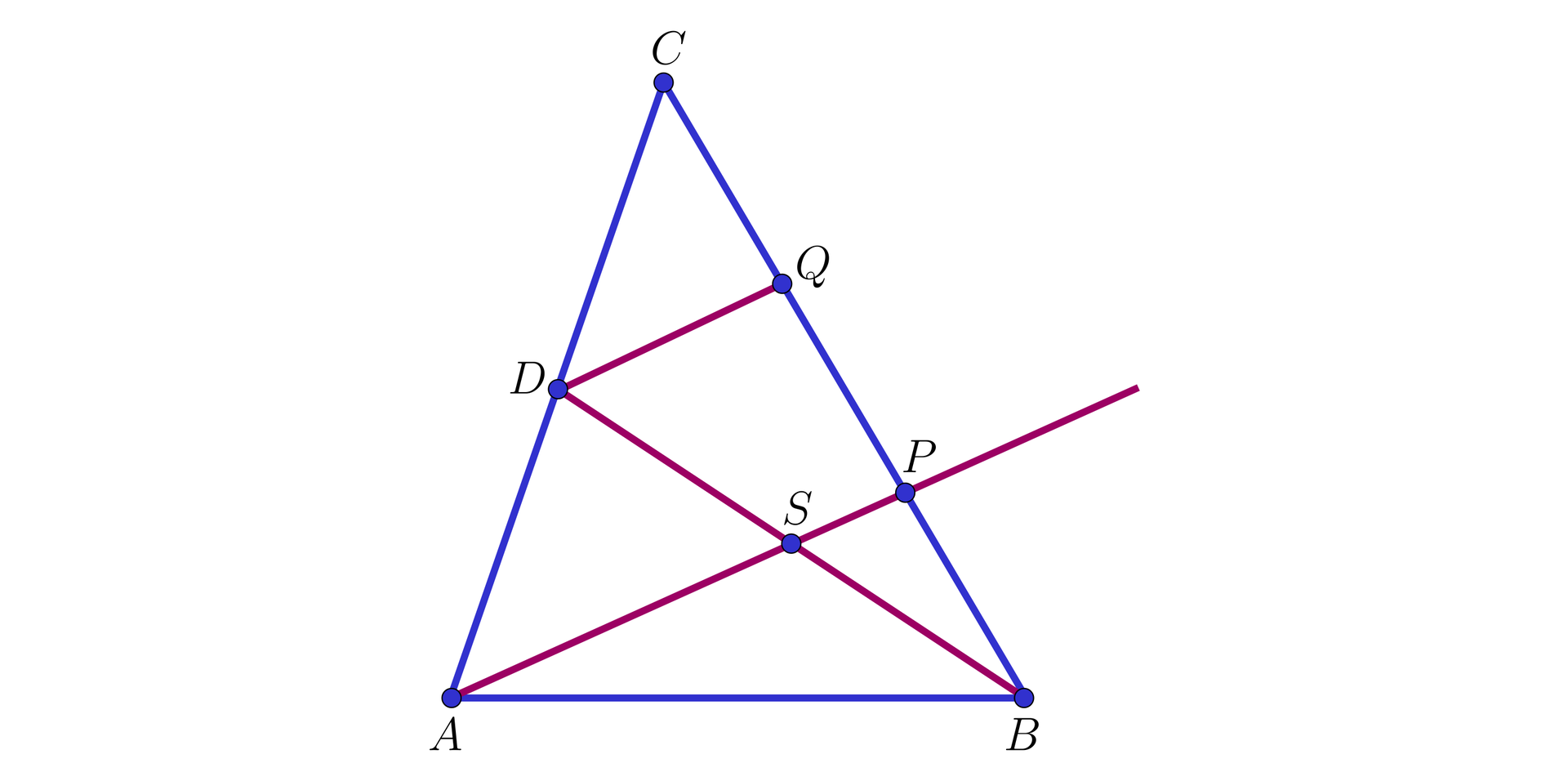
II sposób. Oznaczmy przez
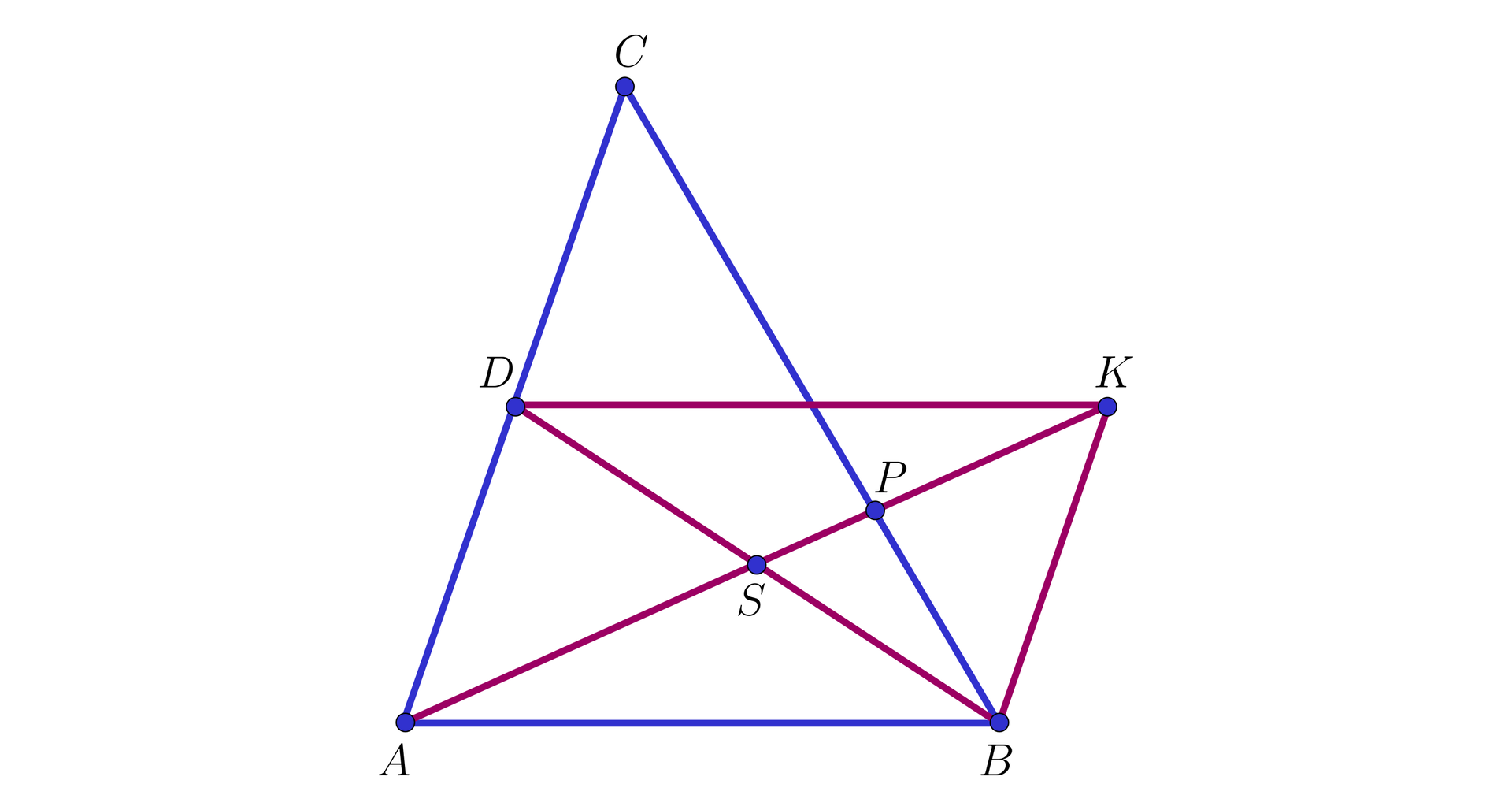
Zatem
Ponieważ
Ponieważ
Wynika stąd, że trójkąty
Oznacza to, że
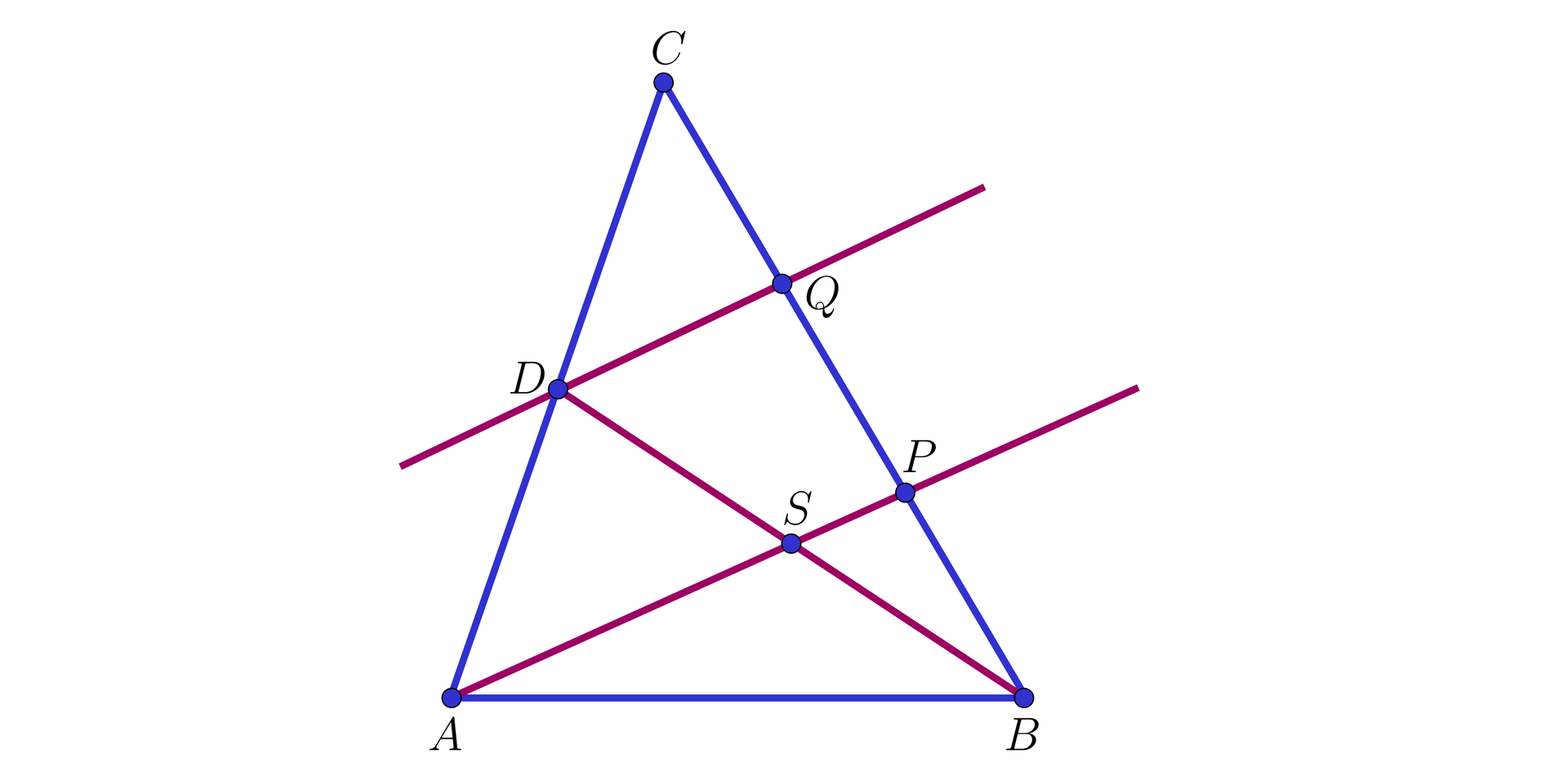
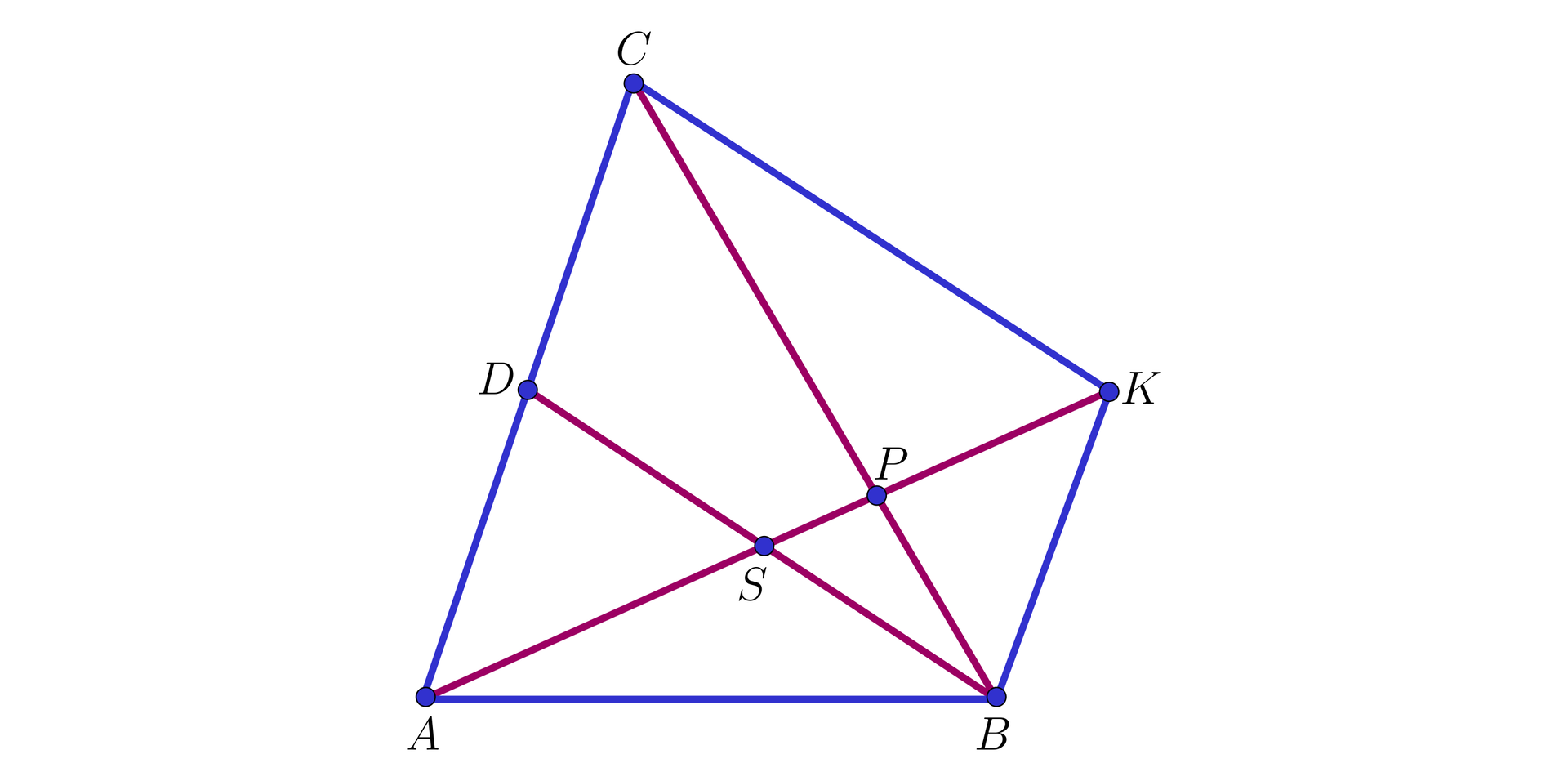
III sposób. Oznaczmy przez
Oznacza to, że
Oznaczmy długość odcinka
Ponieważ punkt
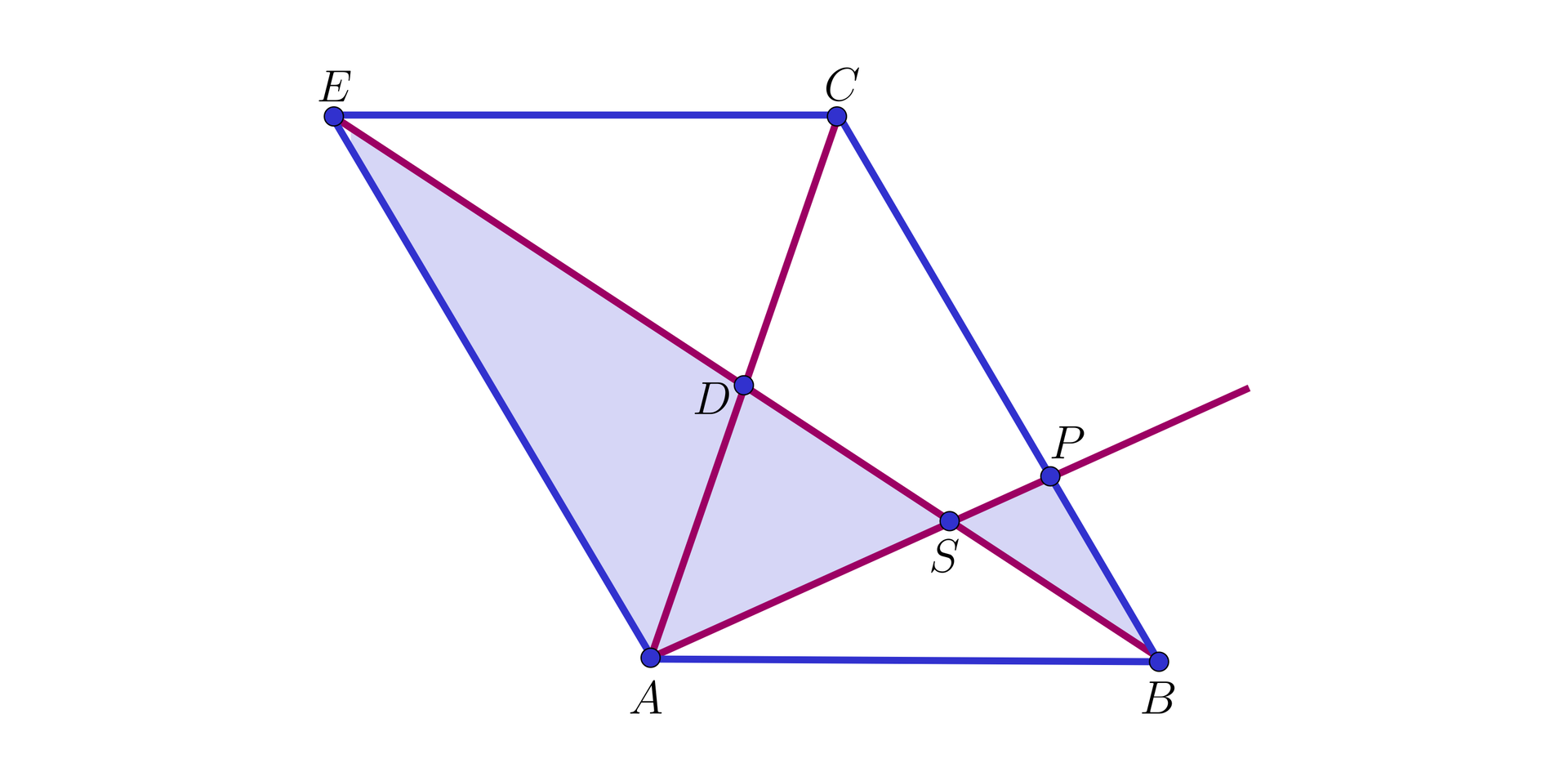
Wobec tego
więc
Koniec dowodu.
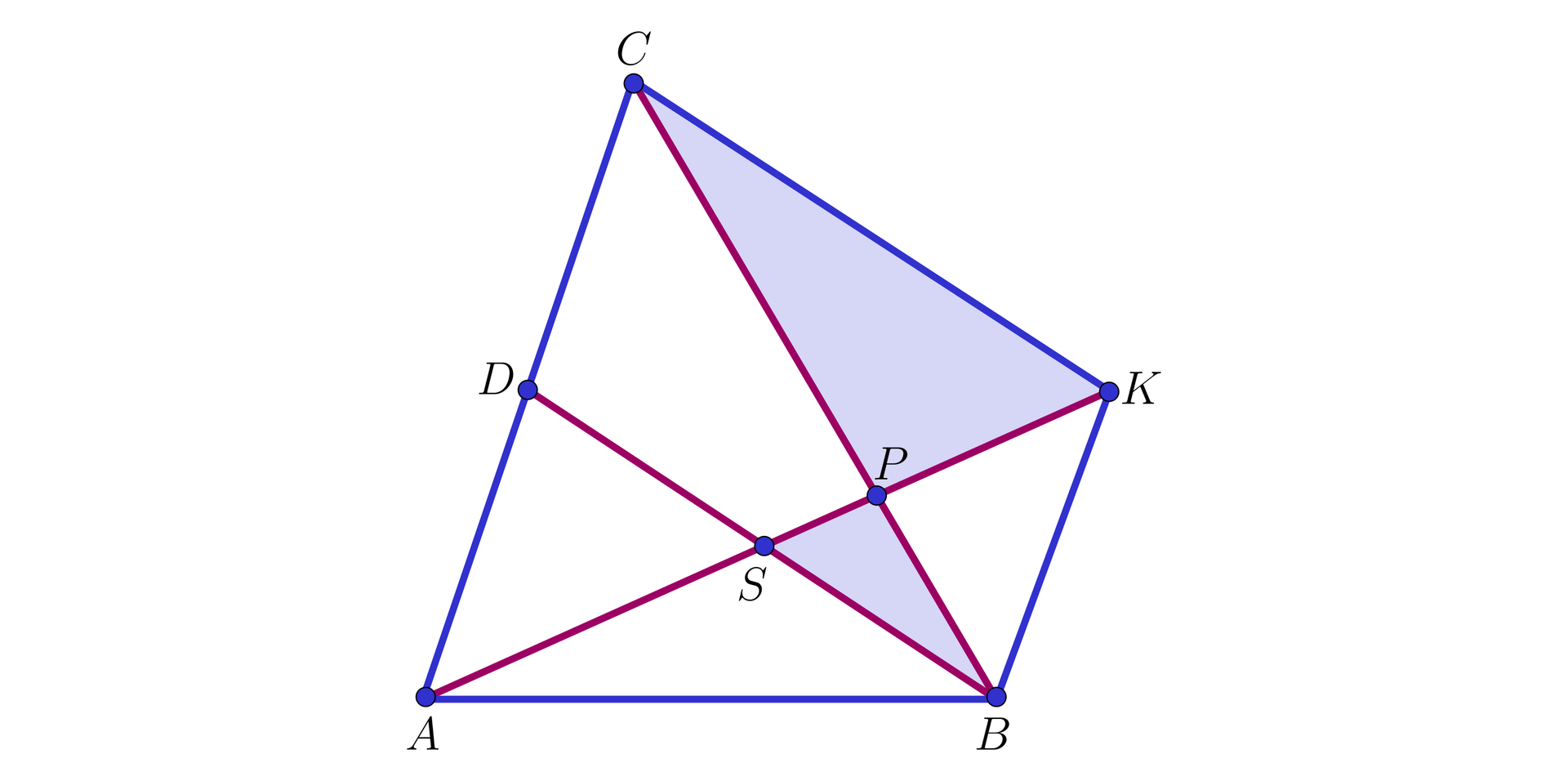
IV sposób. Przyjmijmy, że
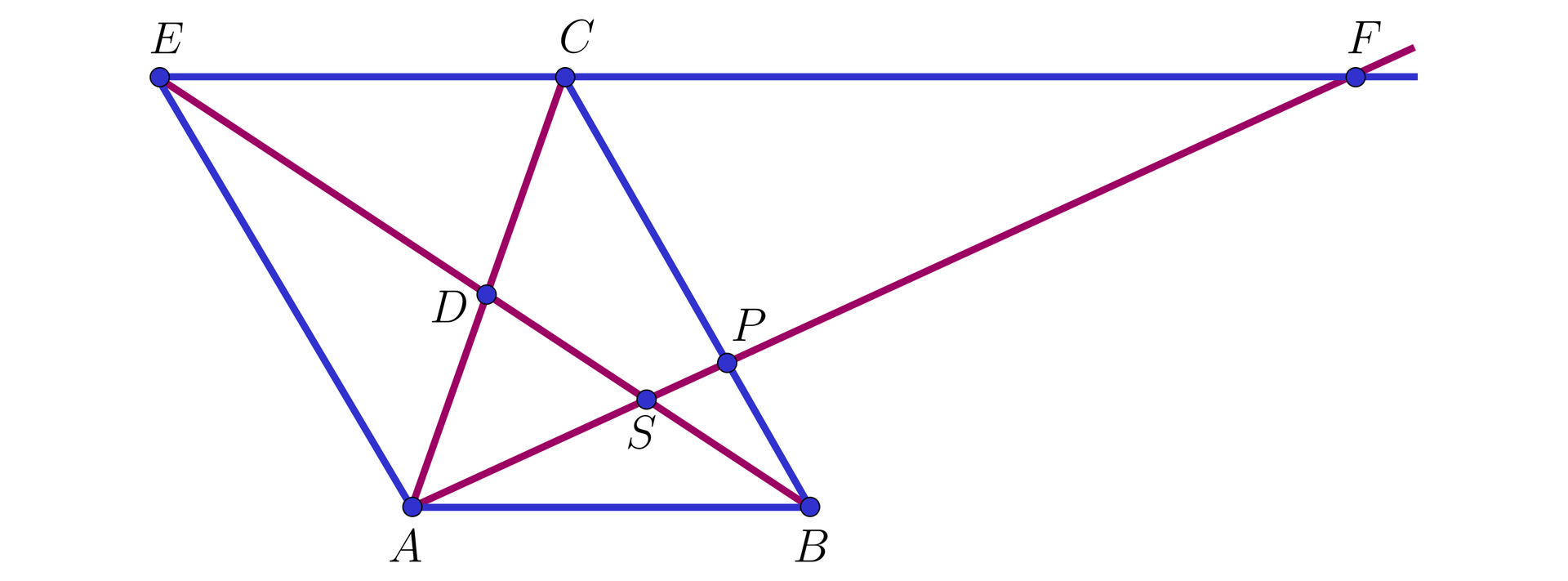
Wtedy czworokąt
Wobec tego trójkąty
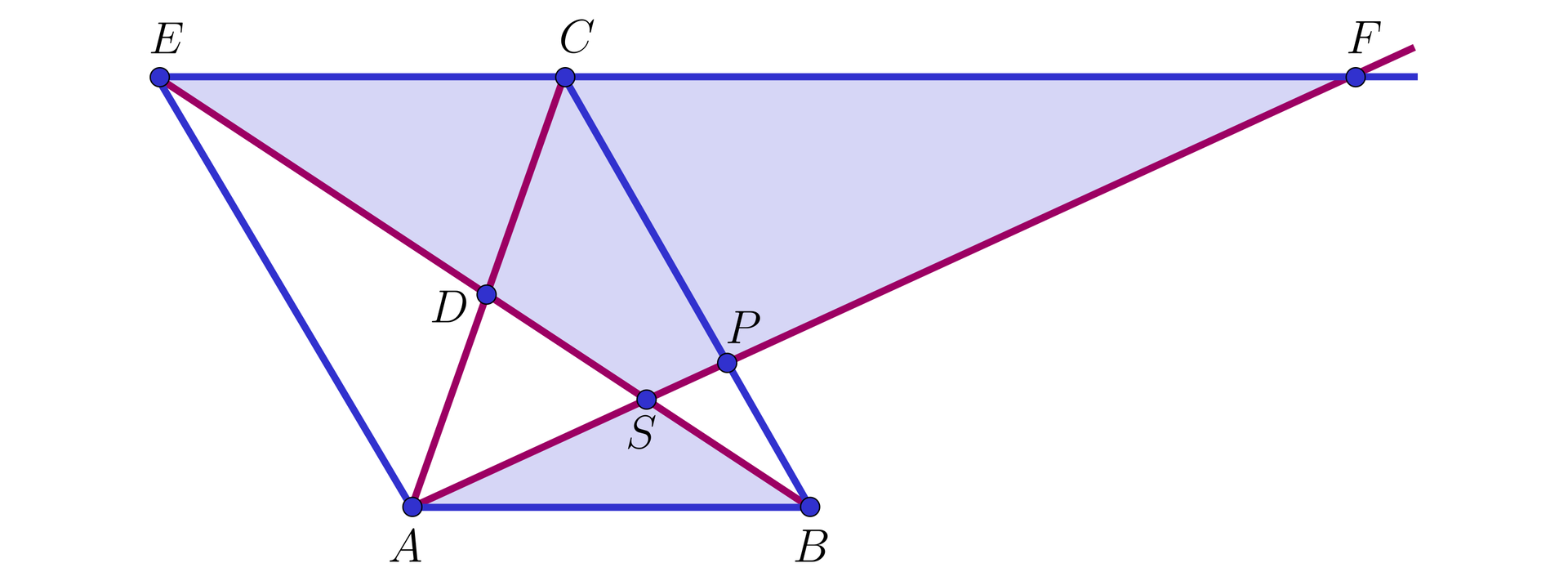
Stąd
Ponieważ
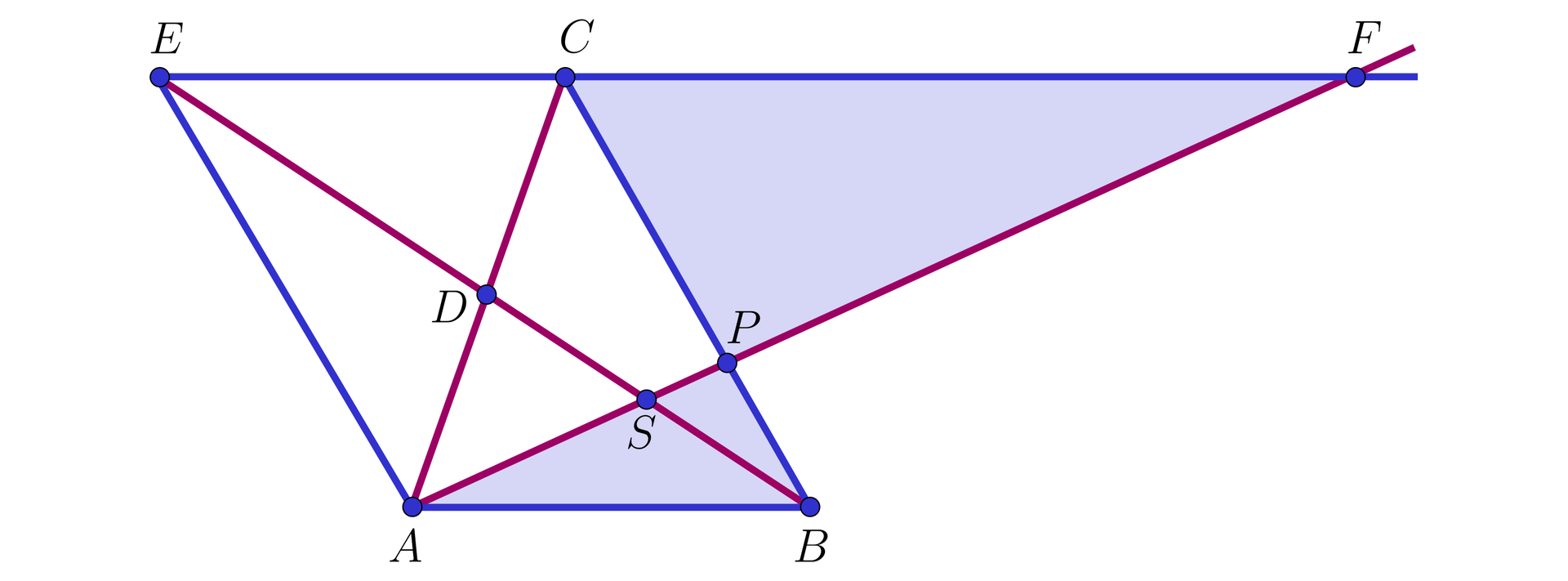
Zatem
Koniec dowodu.
Uwaga. W rozwiązaniu omawianego zadania można (i warto) zastosować znany lemat, który pozwala zapisać proporcję rozpatrywanych odcinków w zależności od pól odpowiednich trójkątów.
Prawdziwa jest mianowicie równość
Ponadto:
ponieważ
S A B D A B S A D S A ponieważ
S D A C S D S A C S D
Wynika stąd, że
Na zakończenie pokażemy, jak wykorzystać podobieństwo trójkątów w dowodach dwóch przydatnych twierdzeń.
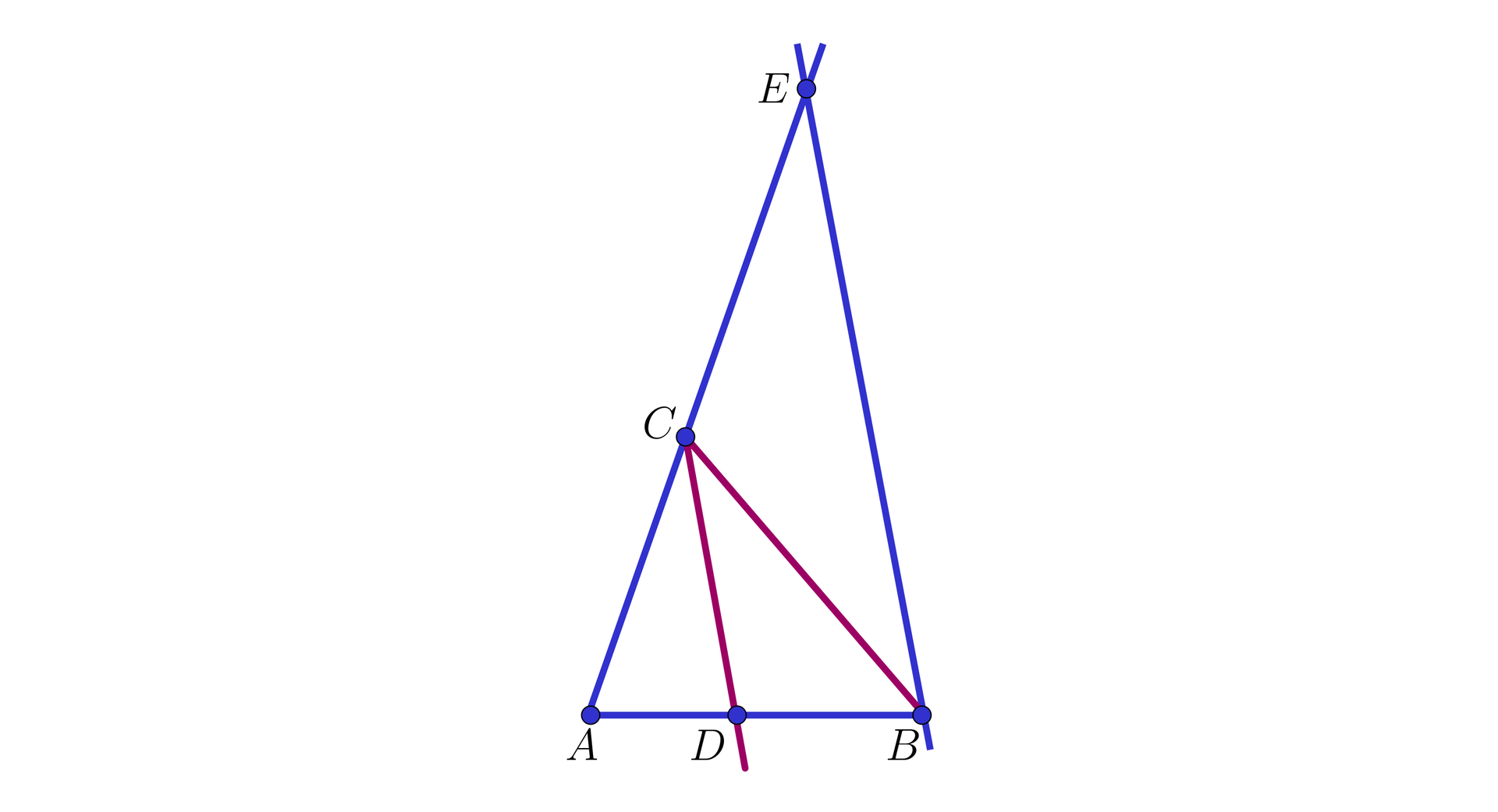
W trójkącie

Prawdziwa jest wtedy równość
Dowód
W szczególnym przypadku, gdy
Bez straty ogólności załóżmy więc, że
A 1 ∈ B C C A 1 = C A B 1 ∈ A C C B 1 = C B
a następnie oznaczmy:
przez
C A A C B A A 1 przez
C B A C B B B 1

Wówczas:
ponieważ w trójkącie
C A A 1 C A C A 1 A C A 1 A A 1 C C A ⊥ A A 1 A C A = C A A 1 ponieważ w trójkącie
C B B 1 C B C B 1 B C B 1 B B 1 C C B ⊥ B B 1 B C B = C B B 1
Wynika stąd, że
(1) trójkąty
(2) trójkąty
Uwzględniając zależności
Na podstawie (1) i (2) możemy zapisać równość
Koniec dowodu.
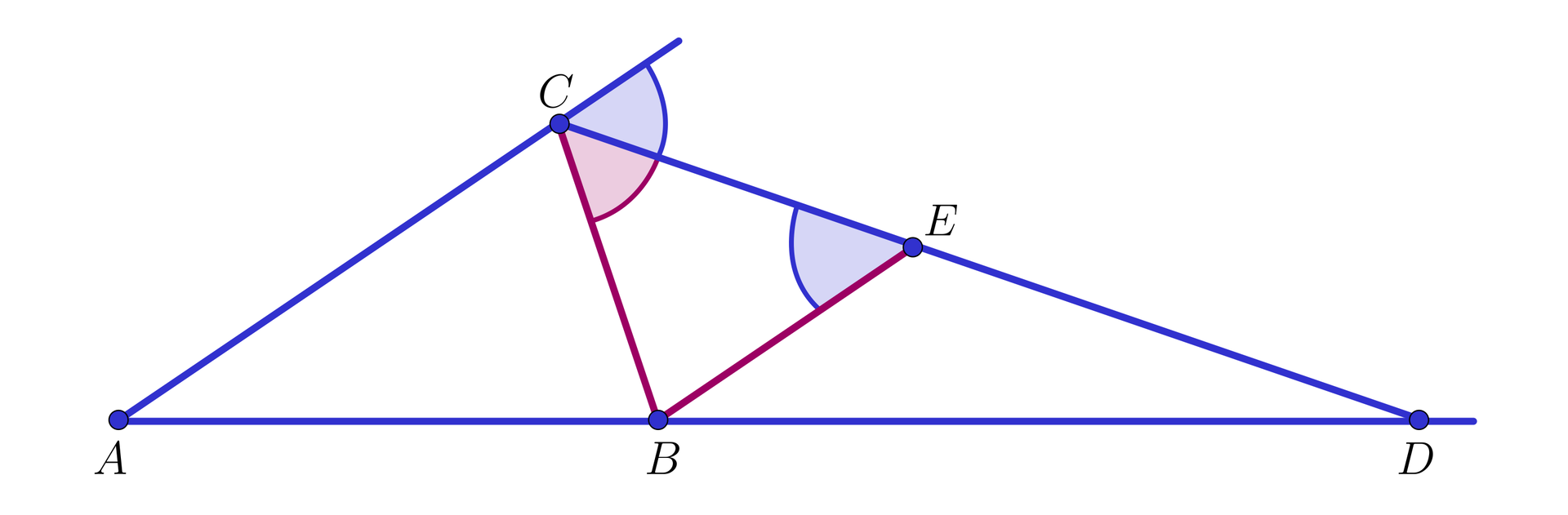
Uwaga
Zatem jeżeli przez punkt
Dla dowodu wystarczy więc udowodnić, że
W tym celu wykażemy, że równe są kąty
Zauważmy mianowicie, że ponieważ proste
równe są kąty odpowiadające
C E B A C D równe są kąty naprzemianległe
D C B C B E

Z założenia wiemy, że
Oznacza to, że w trójkącie
To spostrzeżenie kończy dowód.
Uwaga
ponieważ punkt
D A C B d D A D C A D C P A D C P B D C = 1 2 A C · d 1 2 B C · d = A C B C ponieważ punkty
A D B A D C B D C D h P A D C P B D C = 1 2 A D · h 1 2 B D · h = A D B D
Oznacza to, że
Koniec dowodu.
Uwaga
Stąd
czyli
W ten sposób udowodniliśmy następujące twierdzenie.
Dwusieczna kąta wewnętrznego w trójkącie dzieli przeciwległy bok na odcinki proporcjonalne do długości pozostałych boków tego trójkąta.
Uwaga. Prawdziwe jest następujące twierdzenie o dwusiecznej kąta zewnętrznego w trójkącie.
Dwusieczna kąta zewnętrznego w trójkącie przecina przedłużenie przeciwległego boku w punkcie, którego odległości od końców tego boku są proporcjonalne do długości pozostałych boków.
Zgodnie z oznaczeniami dla trójkąta widocznego na poniższym rysunku dostajemy wtedy równość
Dla dowodu wystarczy poprowadzić z wierzchołka
Czworokąt
Dowód
Zauważmy, że z własności kątów wpisanych opartych na łuku

Wynika stąd, że
Ponieważ
Powyżej udowodniliśmy, że
Zauważmy, że:
równe są kąty wpisane
∢ D A C = ∢ D B C ∢ D A C = ∢ E B C ponieważ czworokąt
A B C D ∢ A D C = 180 ° - ∢ A B C A B C D E C ∢ A B C = ∢ D E C ∢ A D C = 180 ° - ∢ D E C ∢ A D C = ∢ B E C
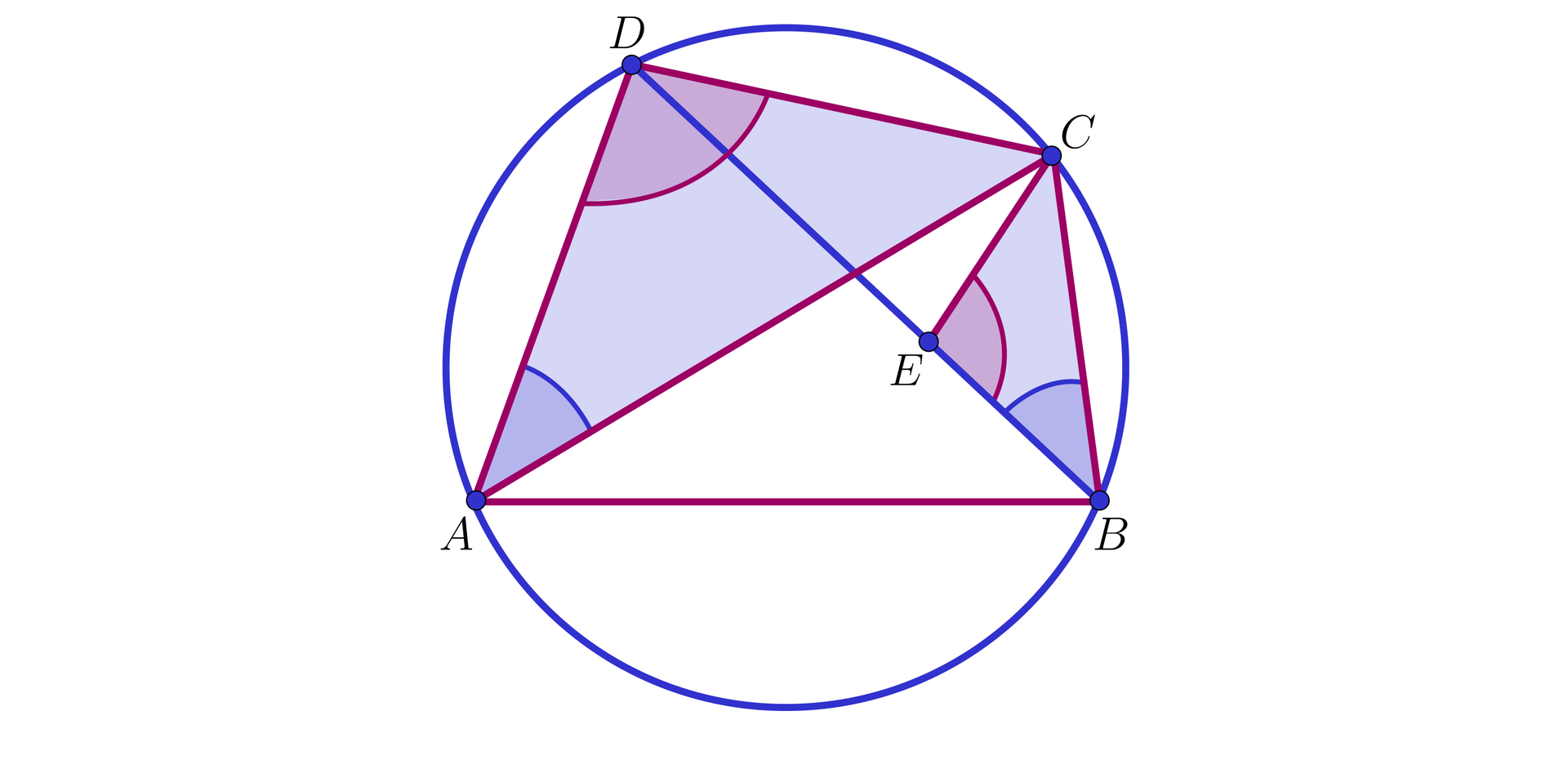
Oznacza to, że trójkąty
Wobec tego zachodzi równość
czyli
W ten sposób wykazaliśmy, że prawdziwe jest następujące twierdzenie.
Jeżeli czworokąt jest wpisany w okrąg, to iloczyn długości jego przekątnych jest równy sumie iloczynów par jego przeciwległych boków.
Uwaga. Prawdziwe jest również twierdzenie odwrotne.
Jeżeli w czworokącie iloczyn długości przekątnych jest równy sumie iloczynów par jego przeciwległych boków, to ten czworokąt da się wpisać w okrąg.
Słownik
trójkąty, w których zachodzi którykolwiek z równoważnych warunków:
cecha kkk: miary par odpowiednich kątów są równe,
cecha bbb: stosunki długości par odpowiednich boków są równe,
cecha bkb: stosunki długości dwóch par boków równe i miary kątów między tymi bokami są równe
stosunek długości pary odpowiadających sobie boków w trójkątach podobnych
odcinek łączący środki dwóch boków w trójkącie jest równoległy do trzeciego boku i równy jego połowie