Przekształcanie wzorów
Wzory matematyczne najczęściej zapisywane są za pomocą równości dwóch wyrażeń algebraicznych. Ich zadaniem jest ułatwienie obliczania niektórych wielkości, np. pola trójkąta objętości graniastosłupa czy prędkości w ruchu jednostajnym. W tym materiale będziemy przekształcać wzory, wyznaczając z nich potrzebne wielkości.
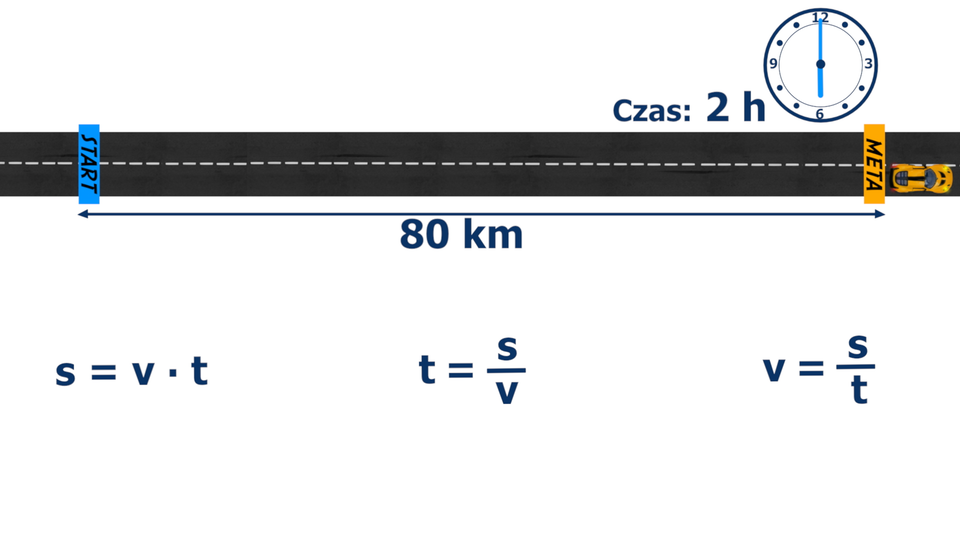
Film dostępny pod adresem /preview/resource/RoFxywga1lwcj
Animacja przedstawia w jaki sposób ze wzoru na prędkość wyznaczyć drogę i czas.
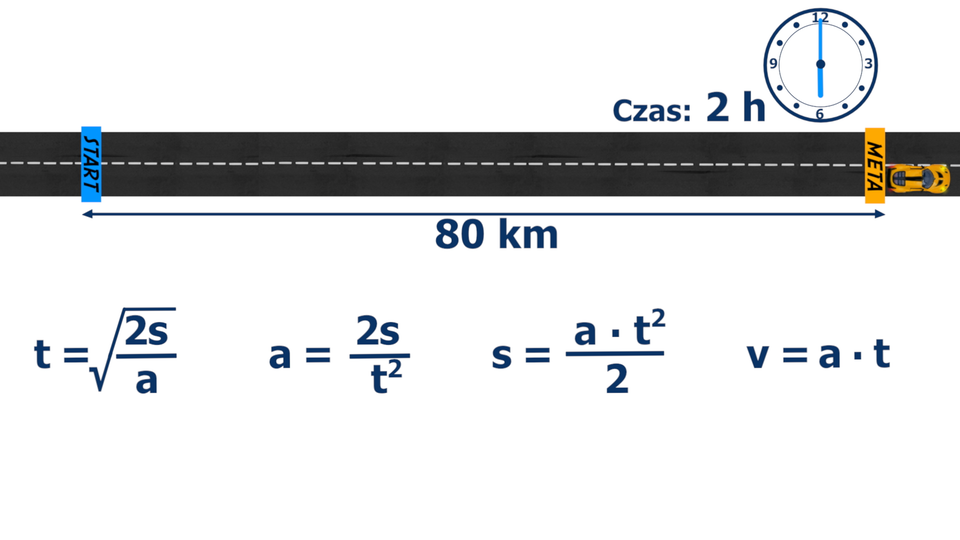
Film dostępny pod adresem /preview/resource/R14BfyWMmAEcJ
Animacja przedstawia jak przekształcić wzór na drogę w ruchu jednostajnie przyspieszonym tak, aby otrzymać wzór na czas i przyspieszenie.

Film dostępny pod adresem /preview/resource/R1WpXiHbGY1mB
Animacja przedstawia w jaki sposób wyznaczyć masę ciała ze wzoru na energię kinetyczną.
Połącz w pary wzór z jego opisem.
wzór na obwód prostokąta, wzór na obwód dowolnego trójkąta, wzór na obwód kwadratu, wzór na obwód trójkąta równobocznego, wzór na obwód trójkąta równoramiennego
| 3a | |
| 2a+b | |
| a+b+c | |
| 2a+2b | |
| 4a |
Przeciągnij i upuść.
, , ,
Jeśli , to ............
Jeśli , to ............
Jeśli , to ............
Jeśli , to ............
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
Z równania wyznacz , , .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
Z równania wyznacz i .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
Z równania wyznacz i .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Z podanego wzoru wyznacz zmienną . Przyjmij, że wszystkie zmienne są różne od zera.
Przeciągnij i upuść.
, , , , , , ,
......................................
......................................
......................................
......................................
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
Z równania wyznacz i .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
Z równania wyznacz i .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
Z równania wyznacz i .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14.
Zmienna wynosi 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. , założenie to 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. .
Z równania wyznacz
Zmienna wynosi 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. .
Z równania wyznacz
Zmienna wynosi 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. , założenie to 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. oraz 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. .
Z równania wyznacz
Zmienna wynosi 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. , założenie to 1. , 2. , 3. , 4. @@, 5. , 6. , 7. @@, 8. .
Zmienna wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. .
Z równania wyznacz .
Zmienna wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , założenie to 1. , 2. , 3. , 4. , 5. , 6. , 7. .
Z równania wyznacz
Zmienna wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. założenie to 1. , 2. , 3. , 4. , 5. , 6. , 7. .
Z równania wyznacz .
Zmienna wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , założenie to 1. , 2. , 3. , 4. , 5. , 6. , 7. .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Ze wzoru wyznacz .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Ze wzoru wyznacz .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Ze wzoru , wyznacz .
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Uszereguj równości w odpowiedniej kolejności, aby ze wzoru wyznaczyć . Podaj konieczne założenia.
Przeciągnij i upuść.
, , , , , , , ,
Start: ....................................
Przekształcenie 1: ....................................
Przekształcenie 2: ....................................
Przekształcenie 3: ....................................
Przekształcenie 4: ....................................
Koniec: ....................................
Założenia: ....................................
Do wzoru podstaw odpowiednio: i . Doprowadź wzór do najprostszej postaci. Wyznacz i oraz podaj konieczne założenia.
Wyszukaj w dostępnych źródłach informacje o zjawisku fizycznym, które opisane jest wzorem. Wyznacz z tego wzoru jedną ze zmiennych.