Pole trójkąta jest równe połowie iloczynu długości dwóch jego boków i sinusa kąta zawartego między tymi bokami.
Przy oznaczeniach takich jak na rysunku

R1Gy7Naw9FVQD1

Rysunek trójkąta rozwartokątnego A B C o bokach długości BC =a, CA =b i AB=c. Kąt rozwarty A C B ma miarę gamma.

Przystawanie trójkątów $\mathrm{ABC}$ i $\mathrm{DEF}$ wynika z każdej z następujących cech przystawania trójkątów:

• cecha przystawania bok‑bok‑bok ($\mathrm{bbb}$)

Trójkąty $\mathrm{ABC}$ i $\mathrm{DEF}$ są przystające wtedy i tylko wtedy, gdy długości boków jednego trójkąta są odpowiednio równe długościom boków drugiego trójkąta.

Rh59rNAjrG2AE1

Rysunek trójkątów przystających A B C oraz D E F z zaznaczonymi różnymi kolorami odpowiadającymi sobie bokami a, b, c.

• cecha przystawania bok‑kąt‑bok ($\mathrm{bkb}$)

Trójkąty $\mathrm{ABC}$ i $\mathrm{DEF}$ są przystające wtedy i tylko wtedy, gdy długości dwóch boków i kąt między tymi bokami w jednym trójkącie są odpowiednio równe dwóm bokom i kątowi między tymi bokami w drugim trójkącie

R1DNusYOOPlhg1

Rysunek trójkątów przystających A B C oraz D E F z zaznaczonymi różnymi kolorami odpowiadającymi sobie bokami a, b i kątem między nimi.

• cecha przystawania kąt‑bok‑kąt ($\mathrm{kbk}$)

Trójkąty $\mathrm{ABC}$ i $\mathrm{DEF}$ są przystające wtedy i tylko wtedy, gdy długości boku i miary kątów przyległych do tego boku w jednym trójkącie są odpowiednio równe długości boku i miarom kątów przyległych do tego boku w drugim trójkącie

R2eaIS7Kc87VQ1

Rysunek trójkątów przystających A B C oraz D E F z zaznaczonymi różnymi kolorami odpowiadającymi sobie kątami i bokiem między nimi.

Jeśli $\mathrm{a }$i $b$ są liczbami nieujemnymi, $n$ i $m$ są liczbami naturalnymi większymi od $1$, $k$ jest dodatnią liczbą naturalną, to

• $\sqrt[n]{a\bullet b}=\sqrt[n]{a}\bullet \sqrt[n]{b}$

• $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$ , $\mathrm{ b}\ne 0$

• ${\left(\sqrt[n]{a}\right)}^n=a$

• ${\left(\sqrt[n]{a}\right)}^k=\sqrt[n]{a^k}$

• $\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\bullet m]{a}$

Jeśli w powyższym twierdzeniu liczby $n$ i $m$ (stopnie pierwiastków) są nieparzyste, to twierdzenie pozostanie prawdziwe również dla ujemnych liczb podpierwiastkowych ($a$ lub $b$) .

Dla dowolnej liczby dodatniej$\mathrm{ a}$ i dowolnych liczb wymiernych $x$ i $y$ prawdziwe są równości

• $a^x\bullet a^y=a^{x+y}$ (wzór na iloczyn potęg o tych samych podstawach)

• $\frac{a^x}{a^{\mathrm{y }}} =a^{x-y}$ (wzór na iloraz potęg o tych samych podstawach)

• ${\left(a^x\right)}^y=a^{x\bullet y}$ (wzór na potęgę potęgi)

• Iloczyn potęg o tych samych podstawach

Dla dowolnej liczby rzeczywistej $a\ne 0$ i dowolnych liczb całkowitych $n$ i $m$ prawdziwa jest równość

R1WKxrD2CezmO1

Animacja

Animacja

Film dostępny na portalu epodreczniki.pl

Animacja

• Iloraz potęg o tych samych podstawach

Dla dowolnej liczby rzeczywistej $a\ne 0$ i dowolnych liczb całkowitych $n$ i $m$ prawdziwa jest równość

R1X2ngJpF9lV01

Animacja

Animacja

Film dostępny na portalu epodreczniki.pl

Animacja

• Potęga potęgi

Dla dowolnej liczby rzeczywistej $a\ne 0$ i dowolnych liczb całkowitych $n$ i $m$ prawdziwa jest równość

R1c65xKTWGhCm1

Animacja

Animacja

Film dostępny na portalu epodreczniki.pl

Animacja

• Iloczyn potęg o tych samych wykładnikach

Dla dowolnych liczb rzeczywistych $a\ne 0$ i  $b\ne 0$ i dowolnej liczby całkowitej $n$ prawdziwa jest równość

RSc0RT5yFz1P31

Animacja

Animacja

Film dostępny na portalu epodreczniki.pl

Animacja

• Iloraz potęg o tych samych wykładnikach

Dla dowolnych liczb rzeczywistych $a\ne 0$ i  $b\ne 0$ i dowolnej liczby całkowitej $n$ prawdziwa jest równość

RXdhHaVVnbedK1

Animacja

Animacja

Film dostępny na portalu epodreczniki.pl

Animacja

Zbiór tych wszystkich liczb rzeczywistych, dla których wzór funkcji ma sens liczbowy nazywamy dziedziną funkcji.

Funkcją $f$ ze zbioru $X$ w zbiór $Y$ nazywamy przyporządkowanie, które każdemu elementowi zbioru $X$ przyporządkowuje dokładnie jeden element zbioru $Y$.
Symbolicznie piszemy $f:X\to Y$. Czytamy „funkcja $f$ odwzorowuje zbiór $X$ w zbiór $Y$”.

• Zbiór $X$ nazywamy dziedziną funkcji, a jego elementy – argumentami funkcji $f$.

• Zbiór $Y$ nazywamy przeciwdziedziną funkcji. Każdy element $y$ zbioru $Y$, który został przyporządkowany co najmniej jednemu argumentowi $x$ nazywamy wartością funkcji $f$ dla argumentu $x$, co zapisujemy symbolicznie $y=f\left(x\right)$. Zbiór $Z$ tych elementów $y$ nazywamy zbiorem wartości funkcji.

Funkcja $\mathrm{f }$jest określona w przedziale $⟨a;b⟩$.
Jeżeli dla dowolnych $x_1,x_2\in ⟨a,b⟩$ takich, że $x_1<x_2$ spełniony jest warunek:

to mówimy, że funkcja $f$ jest malejąca w przedziale $⟨a,b⟩$.

R1JnFIXVvkgJp1

Animacja pokazuje wykres funkcji malejącej.

Animacja pokazuje wykres funkcji malejącej.

Film dostępny na portalu epodreczniki.pl

Animacja pokazuje wykres funkcji malejącej.

Jeśli funkcja, której dziedzinę można podzielić na rozłączne przedziały tak, aby w każdym z nich funkcja ta była monotoniczna, to powiemy, że jest ona monotoniczna przedziałami.

Jeżeli dla dowolnych $x_1,x_2\in ⟨a;b⟩$ takich, że $x_1<x_2$ spełniony jest warunek:

to mówimy, że funkcja $f$ jest niemalejąca w przedziale $⟨a,b⟩$.

Jeżeli dla dowolnych $x_1,x_2\in ⟨a;b⟩$ takich, że $x_1<x_2$ spełniony jest warunek:

To mówimy, że funkcja $f$ jest nierosnąca w przedziale $⟨a,b⟩.$

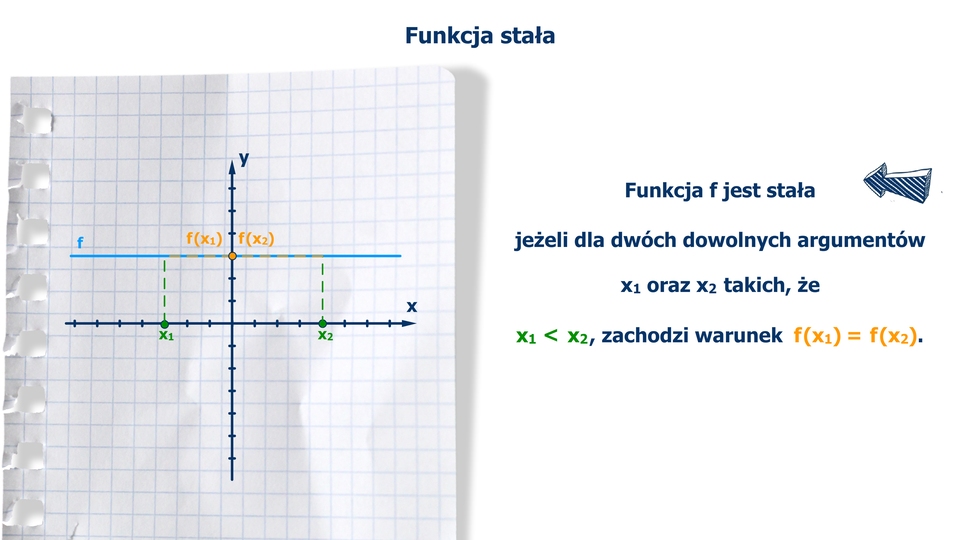
Jeżeli dla dowolnych $x_1,x_2\in ⟨a;b⟩$ takich, że $x_1<x_2$ spełniony jest warunek:

to funkcję $f$ nazywamy stałą w przedziale $⟨a,b⟩$.

RfC9W1bQ7Ip3m1

Animacja pokazuje wykres funkcji stałej.

Animacja pokazuje wykres funkcji stałej.

Film dostępny na portalu epodreczniki.pl

Animacja pokazuje wykres funkcji stałej.

• Kąty: $\alpha$ i ${\alpha }_1$, $\mathrm{ \beta }$ i ${\beta }_1,\mathrm{ \gamma }$ i ${\gamma }_1$ oraz $\delta$ i ${\delta }_1$nazywamy kątami odpowiadającymi.

• Kąty ${\alpha }_1$ i $\delta$ oraz ${\beta }_1$i $\gamma$ nazywamy kątami naprzemianległymi wewnętrznymi.

• Kąty $\beta$ i ${\gamma }_1$ oraz $\alpha$ i ${\delta }_1$ nazywamy kątami naprzemianległymi zewnętrznymi.

  RXoOkGDSnZ9A31

  Rysunek dwóch prostych k i l, które zostały przecięte trzecią prostą c. Pomiędzy tymi prostymi powstały kąty odpowiadające oraz kąty naprzemianległe.

  

• Kąty przyległe to dwa kąty, które mają jedno ramię wspólne, a pozostałe ramiona dopełniają się do prostej.

• Kąty wierzchołkowe to dwa kąty, które mają wspólny wierzchołek i przedłużeniem ramion jednego kąta są odpowiednie ramiona drugiego kąta.

  R17EFmv3QSulO1

  Rysunek dwóch prostych przecinających się. Między prostymi zaznaczone dwie pary kątów wierzchołkowych: alfa i beta oraz delta i gamma.

  

  Na przykład $\alpha$ i $\gamma$ na rysunku są kątami przyległymi. Pary kątów wierzchołkowych to $\alpha$ i $\beta$ oraz $\gamma$ i $\delta .$

Każdy argument, dla którego funkcja przyjmuje wartość $0$ nazywamy miejscem zerowym tej funkcji.

Jeżeli suma kwadratów długości dwóch boków trójkąta jest równa kwadratowi długości trzeciego boku, to trójkąt jest prostokątny.

Dwusieczne każdego z kątów w trójkącie przecinają się w jednym punkcie.
Punkt ten jest środkiem okręgu wpisanego w ten trójkąt.

RmHLgU2tM0aZa1

Rysunek trójkąta A B C, którego dwusieczne kątów przecinają się w jednym punkcie S. Punkt ten jest środkiem okręgu wpisanego w ten trójkąt.

Odcinki łączące środek $S$ okręgu wpisanego w trójkąt $\mathrm{ABC}$ z wierzchołkami tego trójkąta podzieliły trójkąt na trzy trójkąty $\mathrm{ABS}$, $\mathrm{BCS}$ i $\mathrm{ACS}$.
Wysokość każdego z tych trójkątów jest równa promieniowi okręgu wpisanego w trójkąt $\mathrm{ABC}$ (jak na rysunku).

RTFTlSi6QYHce1

Rysunek trójkąta A B C o bokach długości a, b i c. Dwusieczne kątów przecinają się w jednym punkcie S. Punkt ten jest środkiem okręgu, o promieniu r wpisanego w ten trójkąt.

Pole trójkąta $\mathrm{ABC}$ jest równe sumie pól trójkątów $\mathrm{BCS}$, $\mathrm{ACS}$ i $\mathrm{ABS}$

Wyprowadziliśmy w ten sposób wzór na pole trójkąta, w którym występują długości jego boków oraz promień okręgu wpisanego w ten trójkąt.

Kąty wierzchołkowe są równe.

Odcinek łączący środki ramion trapezu jest równoległy do podstaw tego trapezu, a jego długość jest równa średniej arytmetycznej długości podstaw trapezu.

RLFCoKQvm4KfS1

Animacja pokazuje w pięciu krokach dowód na podaną regułę. W trapezie A B C D z zaznaczono podstawę górną a i podstawą dolną b. Poprowadzono przekątną AC i oznaczono jej środek przez G. Następnie oznaczono przez E i F odpowiednio środki odcinków AD i BC. Zauważamy, że stosunek długości odcinków DC i EG wynosi 1 do 2. Odcinek EG jest linią środkową w trójkącie A C D, czyli jest równoległy do podstawy DC i równy 0,5a. Odcinek AB jest dwa razy dłuższy od odcinka GF, więc odcinek GF jest linią środkową w trójkącie A B C, czyli jest równoległy do podstawy AB i równy 0,5b. Odcinki EG i GF są częścią prostej równoległej do podstawy trapezu i przechodzącej przez punkt G, stąd długość linii środkowej w trapezie jest równa połowie sumy długości podstaw trapezu a i b.

Animacja pokazuje w pięciu krokach dowód na podaną regułę. W trapezie A B C D z zaznaczono podstawę górną a i podstawą dolną b. Poprowadzono przekątną AC i oznaczono jej środek przez G. Następnie oznaczono przez E i F odpowiednio środki odcinków AD i BC. Zauważamy, że stosunek długości odcinków DC i EG wynosi 1 do 2. Odcinek EG jest linią środkową w trójkącie A C D, czyli jest równoległy do podstawy DC i równy 0,5a. Odcinek AB jest dwa razy dłuższy od odcinka GF, więc odcinek GF jest linią środkową w trójkącie A B C, czyli jest równoległy do podstawy AB i równy 0,5b. Odcinki EG i GF są częścią prostej równoległej do podstawy trapezu i przechodzącej przez punkt G, stąd długość linii środkowej w trapezie jest równa połowie sumy długości podstaw trapezu a i b.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dot1EGQXY

Symetralne trzech boków trójkąta przecinają się w jednym punkcie.
Punkt ten jest środkiem okręgu opisanego na tym trójkącie.

R1DdQegoGHm371

Rysunek trójkąta A B C, którego symetralne przecinają się w jednym punkcie. Trójkąt jest wpisany w okrąg o środku w punkcie S.

W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej

R1NhwQt45irzA1

Rysunek trójkąta prostokątnego o przyprostokątnych długości a i b oraz przeciwprostokątnej c.

Pole trójkąta o bokach długości $a$, $b$, $c$ oraz promieniu $r$ okręgu wpisanego w ten trójkąt wyraża się wzorem

Gdy oznaczymy $\frac{a+b+c}{2}=p$, wzór przyjmuje postać $P=\mathrm{pr}$.

Pole wycinka koła o promieniu r i kącie $\alpha$ jest równe

Dla dowolnej liczby nieujemnej $a$ i liczby naturalnej $n$ większej od $1$ przyjmujemy

Funkcja $f$, opisująca zależność między dodatnimi wielkościami wprost proporcjonalnymi $x$ i $y$ nazywana jest proporcjonalnością prostą, a iloraz $\frac{y}{x}$ nazywamy współczynnikiem tej proporcjonalności. Oznaczając ten współczynnik przez $a$, zapisujemy funkcję $f$ wzorem

gdzie $x>0$.
Uwaga: Wprost z definicji wynika, że $a>0$.

Dwie zmienne wielkości dodatnie nazywamy wprost proporcjonalnymi, jeżeli iloraz tych wielkości jest stały.

Jeżeli trójkąt $\mathrm{A\text{'}B\text{'}C\text{'}}$ jest podobny do trójkąta $\mathrm{ABC}$ w skali podobieństwa $k$, to stosunek obwodów tych trójkątów jest równy skali podobieństwa, a stosunek ich pól jest równy kwadratowi skali podobieństwa

Wycinkiem koła nazywamy każdą z dwóch jego części wyznaczonych przez dwa promienie tego koła wraz z tymi promieniami. Kąt pomiędzy tymi promieniami nazywamy kątem wycinka.

R1Ln1hoIdTjvs1

Rysunek koła o środku S z zaznaczonym wycinkiem koła o kącie ASC =alfa.

Wykresem funkcji $f\left(x\right)=\mathrm{ax}$, gdzie $a$ to ustalona liczba rzeczywista, jest prosta o równaniu $y=\mathrm{ax}$.

Jeżeli liczbę dodatnią zaokrąglamy do ustalonego rzędu wielkości, np. do tysięcy, setek, dziesiątek, jedności, części dziesiątych, części setnych itd., to wszystkie cyfry stojące po prawej stronie ostatniej (licząc od strony lewej) cyfry znaczącej zastępujemy zerami. Z cyframi znaczącymi postępujemy następująco:

• gdy pierwsza cyfra z prawej strony ostatniej cyfry znaczącej jest mniejsza od $5$, to wszystkie cyfry znaczące pozostawiamy bez zmian,

• gdy pierwsza cyfra z prawej strony ostatniej cyfry znaczącej jest co najmniej równa $5$, a ostatnia cyfra znacząca jest mniejsza od $9$, to tę cyfrę zwiększamy o $1$, a wszystkie poprzednie cyfry znaczące pozostawiamy bez zmian. Jeśli natomiast ostatnią cyfrą znaczącą jest $9$, to zamiast niej piszemy cyfrę $0$ i tę samą procedurę stosujemy do poprzednich cyfr znaczących.