Sprawdź się
Uzupełnij tekst poprzez przeciągnięcie poprawnych odpowiedzi.
przystającego, tym samym, rozwartego, środkowego, ostrego, zewnętrznego, taki sam, odwrotnie proporcjonalny, przeciwny
Wycinkiem koła nazywamy część koła ograniczoną przez ramiona kąta ................................................ i łuk oparty na ................................................ kącie. Stosunek kąta środkowego do kąta pełnego jest ................................................, jak stosunek pola powierzchni wycinka kołowego do pola powierzchni całego koła.
Wskaż grafikę na której zaznaczony wycinek koła ma największe pole powierzchni.
- Opis ilustracji A
- Opis ilustracji B
- Opis poprawnej C
- Opis ilustracji D
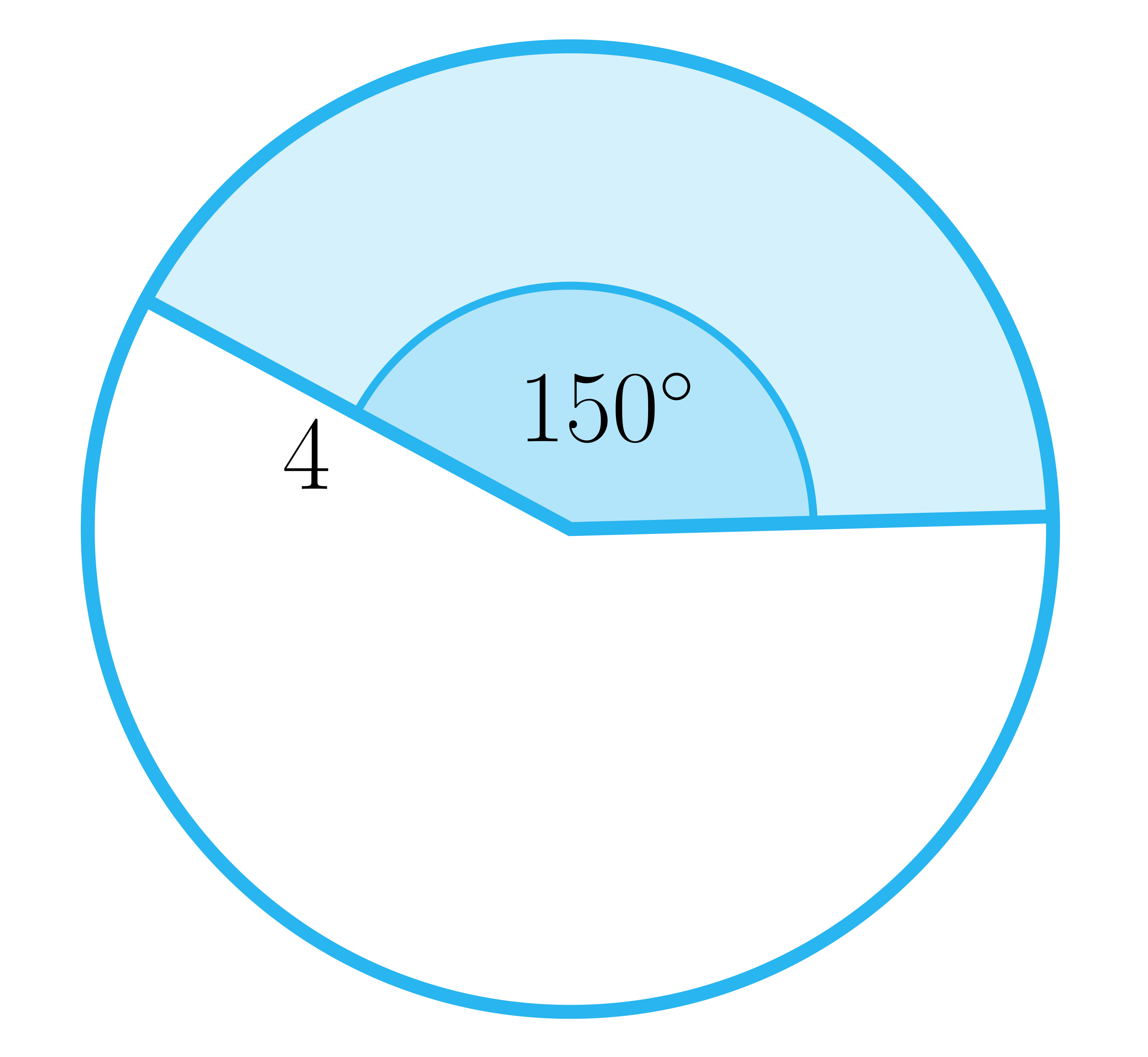

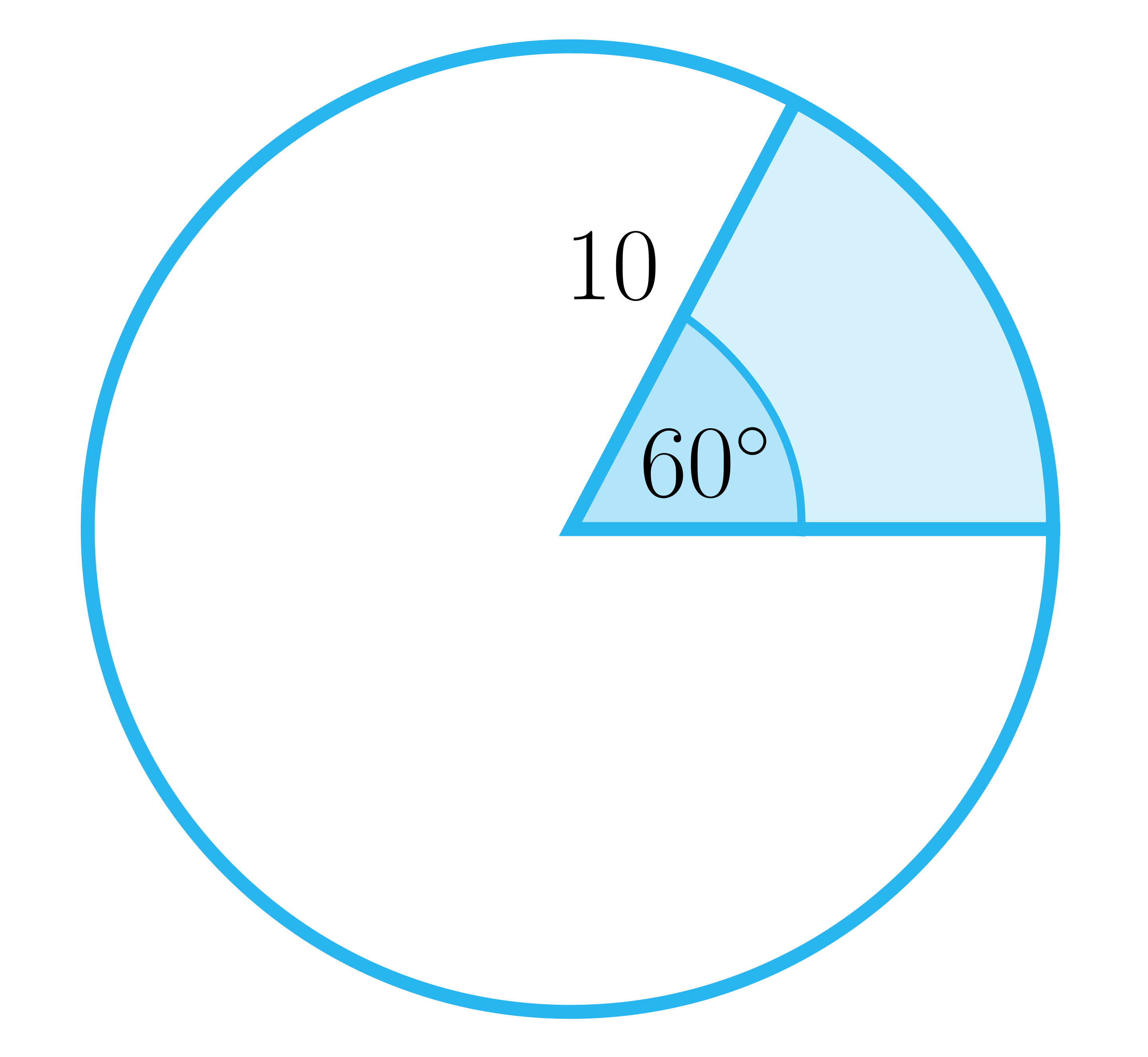

Zaznacz prawidłową odpowiedź. Jaką miarę ma kąt środkowy, jeśli pole powierzchni wycinka koła wynosi , zaś długość promienia tego okręgu wynosi ?
Zaznacz poprawną odpowiedź. Jakie pole powierzchni ma koło, w którym kątowi środkowemu odpowiada wycinek kołowy o powierzchni .
Pole wycinka kołowego wynosi i stanowi ono pola koła. Znajdź miarę kąta środkowego odpowiadającego temu wycinkowi oraz promień koła. Uzupełnij pola.
Kąt środkowy wyznaczający ten wycinek ma miarę .............
Rozważane koło ma promień ............ .
Z krótszych brzegów prostokąta wycięto dwa półkola, Każde z nich miało średnicę równą długości krótszego z boków, tj. . Dłuższy bok prostokąta ma długość .
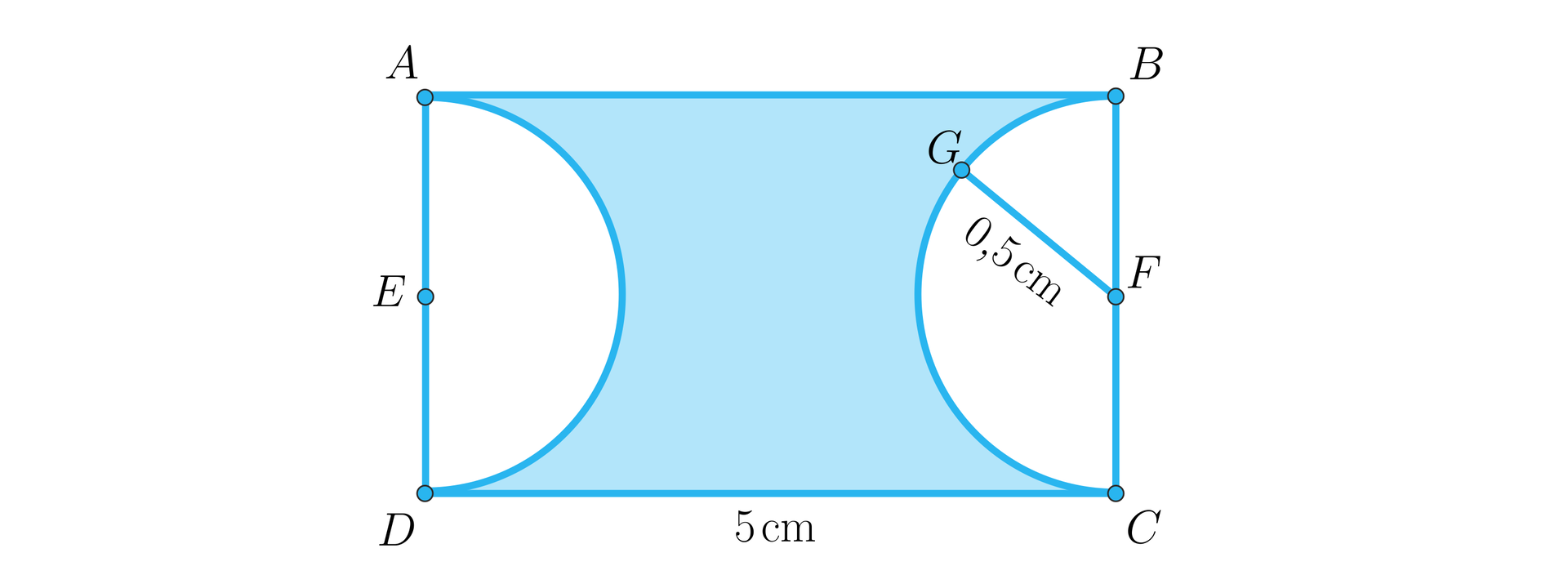
Oblicz pole zacieniowanego obszaru.
Zaznacz poprawną odpowiedź. W przeciwległych wierzchołkach kwadratu zostały narysowane koła, których promienie stanowiły boki tego kwadratu (których długość wynosi ). Pole powierzchni fragmentu kwadratu, który stanowi część wspólną wnętrz owych kół wyraża się wzorem:
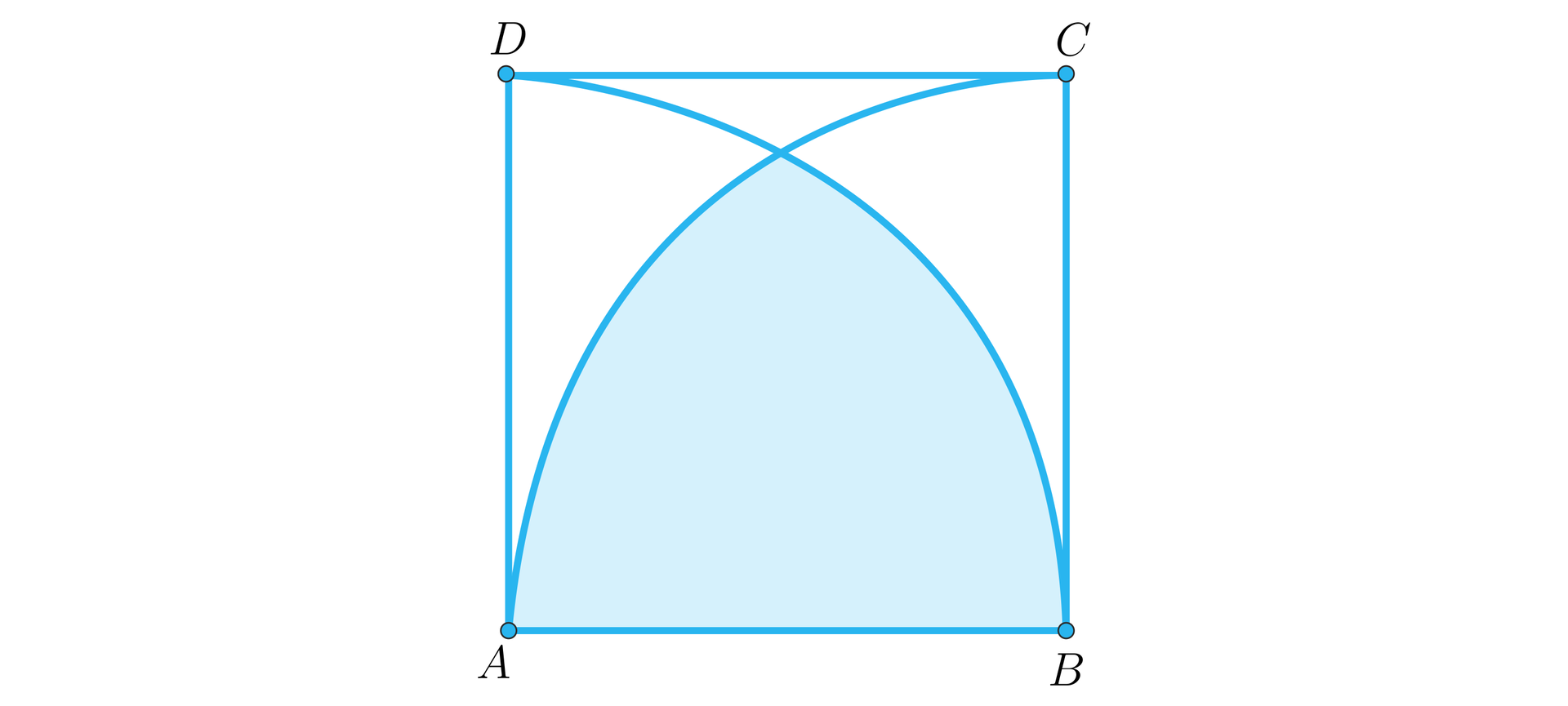
Oblicz pole zaznaczonego obszaru, jeśli czworokąt jest kwadratem o boku , zaś krzywe i są łukami okręgów o środkach w punktach odpowiednio i .
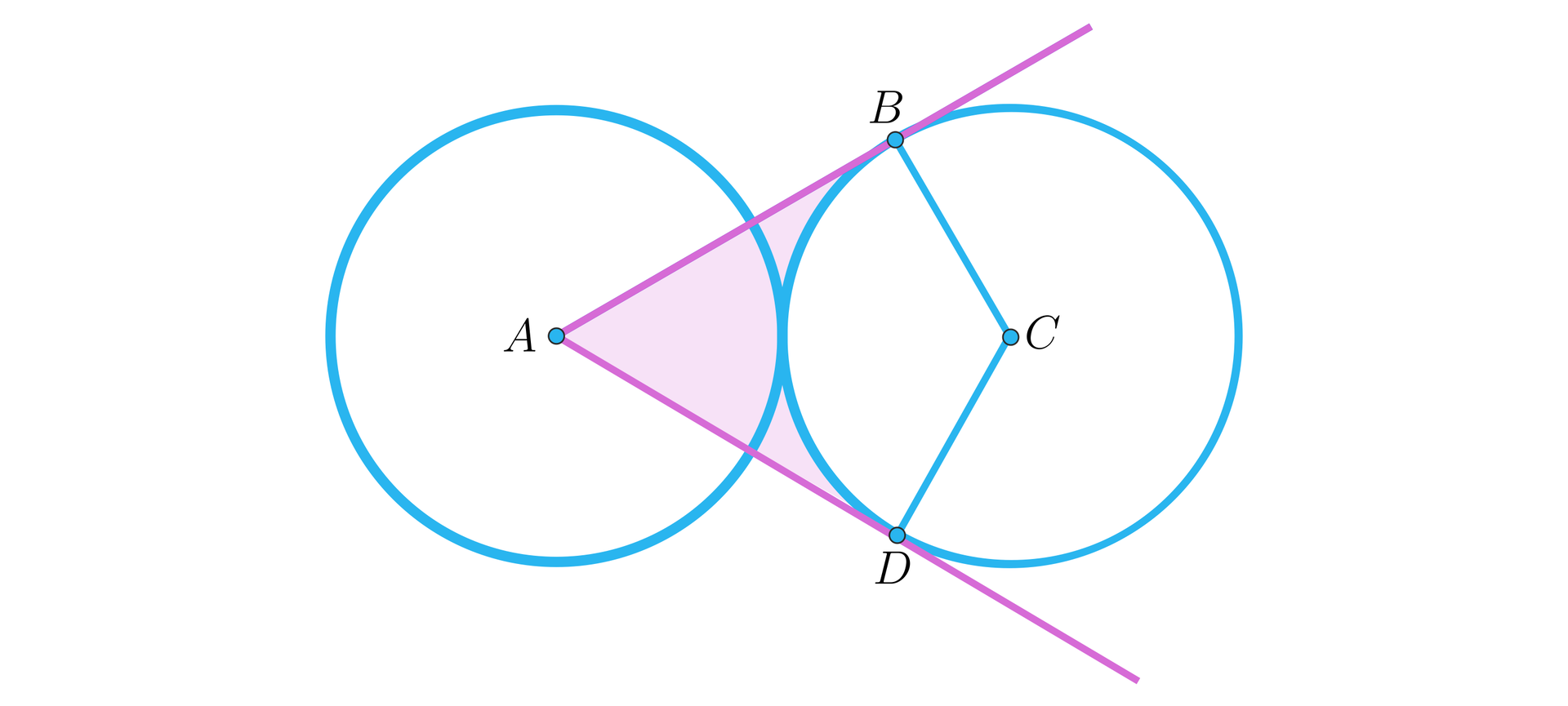
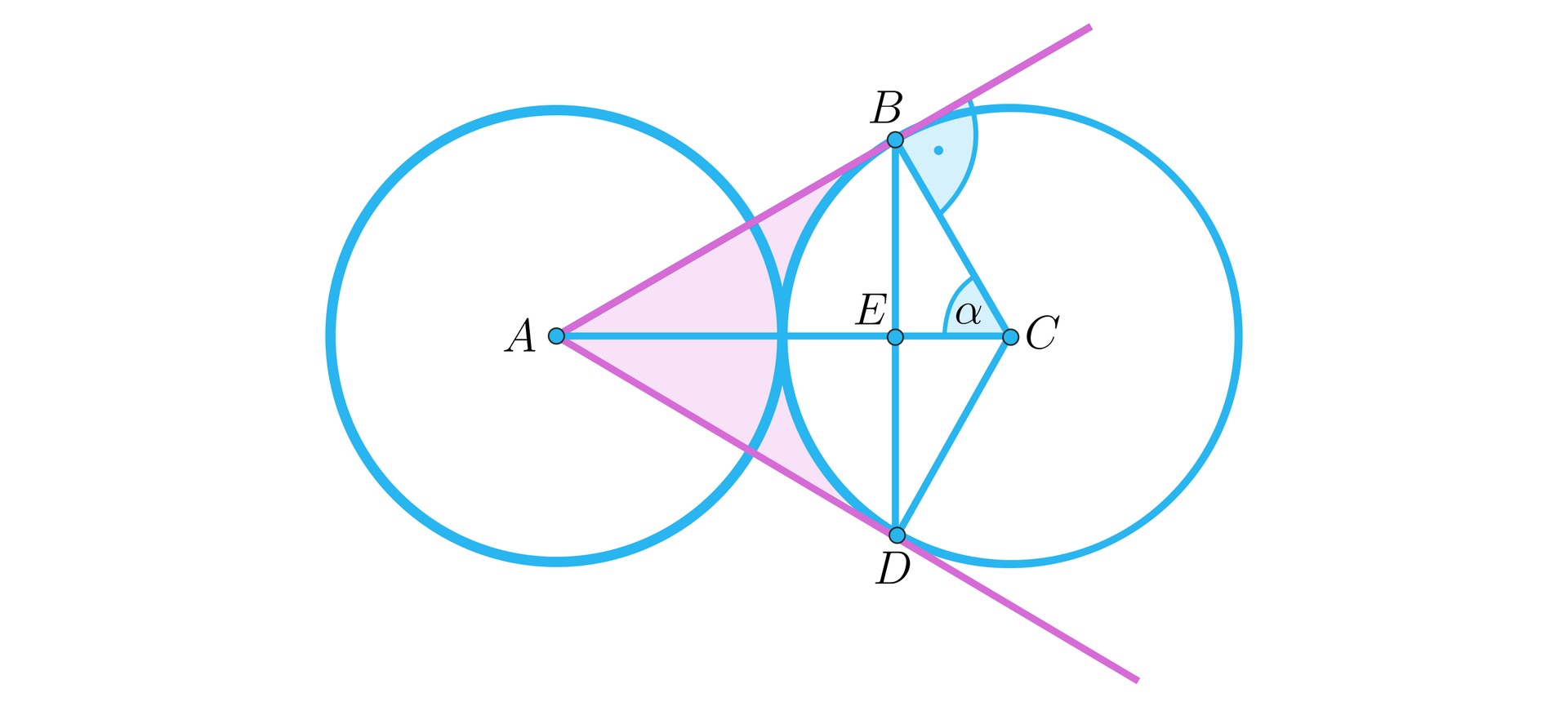
Okręgi o środkach w punktach i mają ten sam promień i są do siebie styczne. Ze środka pierwszego z nich poprowadzono półproste styczne do drugiego okręgu – punkty styczności oznaczono odpowiednio literami i . Oblicz pole zaznaczonego obszaru, wiedząc, że długość promienia w każdym z tych okręgów wynosi .