Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

RHdTuDwvbfEQK

R1RZTD9CVoews

R1JC1DJIpznvP1

Ćwiczenie 2

	Prawda	Fałsz
Prostokąt o długości $2 π r$ może być powierzchnią boczną jakiegoś walca.	□	□
Walec ma wysokość $4$ i promień równy $4$ . W siatce tego walca powierzchnia boczna będzie kwadratem..	□	□
W walcu o promieniu podstawy $\frac{3}{π}$ i wysokości $2 π$ powierzchnia boczna jest prostokątem o bokach, których długości są liczbami wymiernymi.	□	□
Jeżeli w siatce walca powierzchnia boczna jest kwadratem, to wysokość tego walca jest $π$ -krotnie dłuższa od promienia podstawy.	□	□

Ćwiczenie 3

Na którym z rysunku (jedna kratka, to jedna jednostka) przedstawiono siatkę walca znajdującego się poniżej:

RHdBZL3a732a1

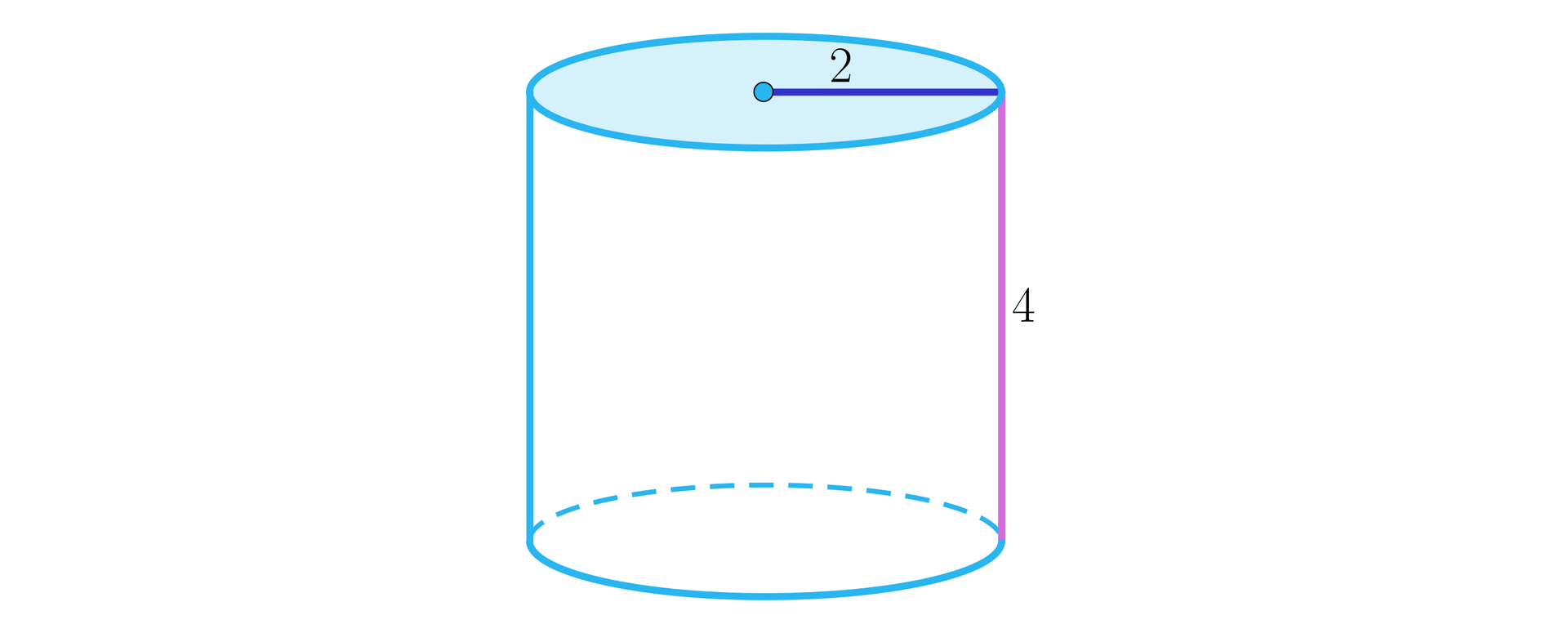
Ilustracja przedstawia walec o promieniu podstawy o długości dwa oraz wysokości o długości cztery.

R1I0rOaaKbh4i

Rk4kVFQ4cbDlZ

Ćwiczenie 4

R1LSmoUdI4SBQ

R1CR7Qm5LQjFv

Krótszy bok prostokąta# Możliwe odpowiedzi: 1. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa sześć., 2. Ilustracja przedstawia siatkę walca. Prostokąt ma wymiary równe cztery pi oraz trzy., 3. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa półtorej., 4. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równą trzy. Suma dwóch średnic okręgów oraz długości prostokąta wynosi siedem. Prosta przechodząca przez środki dłuższych boków prostokąta Możliwe odpowiedzi: 1. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa sześć., 2. Ilustracja przedstawia siatkę walca. Prostokąt ma wymiary równe cztery pi oraz trzy., 3. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa półtorej., 4. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równą trzy. Suma dwóch średnic okręgów oraz długości prostokąta wynosi siedem. Dłuższy bok prostokąta Możliwe odpowiedzi: 1. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa sześć., 2. Ilustracja przedstawia siatkę walca. Prostokąt ma wymiary równe cztery pi oraz trzy., 3. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa półtorej., 4. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równą trzy. Suma dwóch średnic okręgów oraz długości prostokąta wynosi siedem. Prosta przechodząca przez środki krótszych boków prostokąta Możliwe odpowiedzi: 1. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa sześć., 2. Ilustracja przedstawia siatkę walca. Prostokąt ma wymiary równe cztery pi oraz trzy., 3. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równy dwa, średnica okręgu jest równa półtorej., 4. Ilustracja przedstawia siatkę walca. Prostokąt ma długość równą trzy. Suma dwóch średnic okręgów oraz długości prostokąta wynosi siedem.

Ćwiczenie 5

Promień podstawy jest dwukrotnie krótszy od wysokości walca, którego siatkę przedstawiono poniżej.

RU8wZiAK2kY94

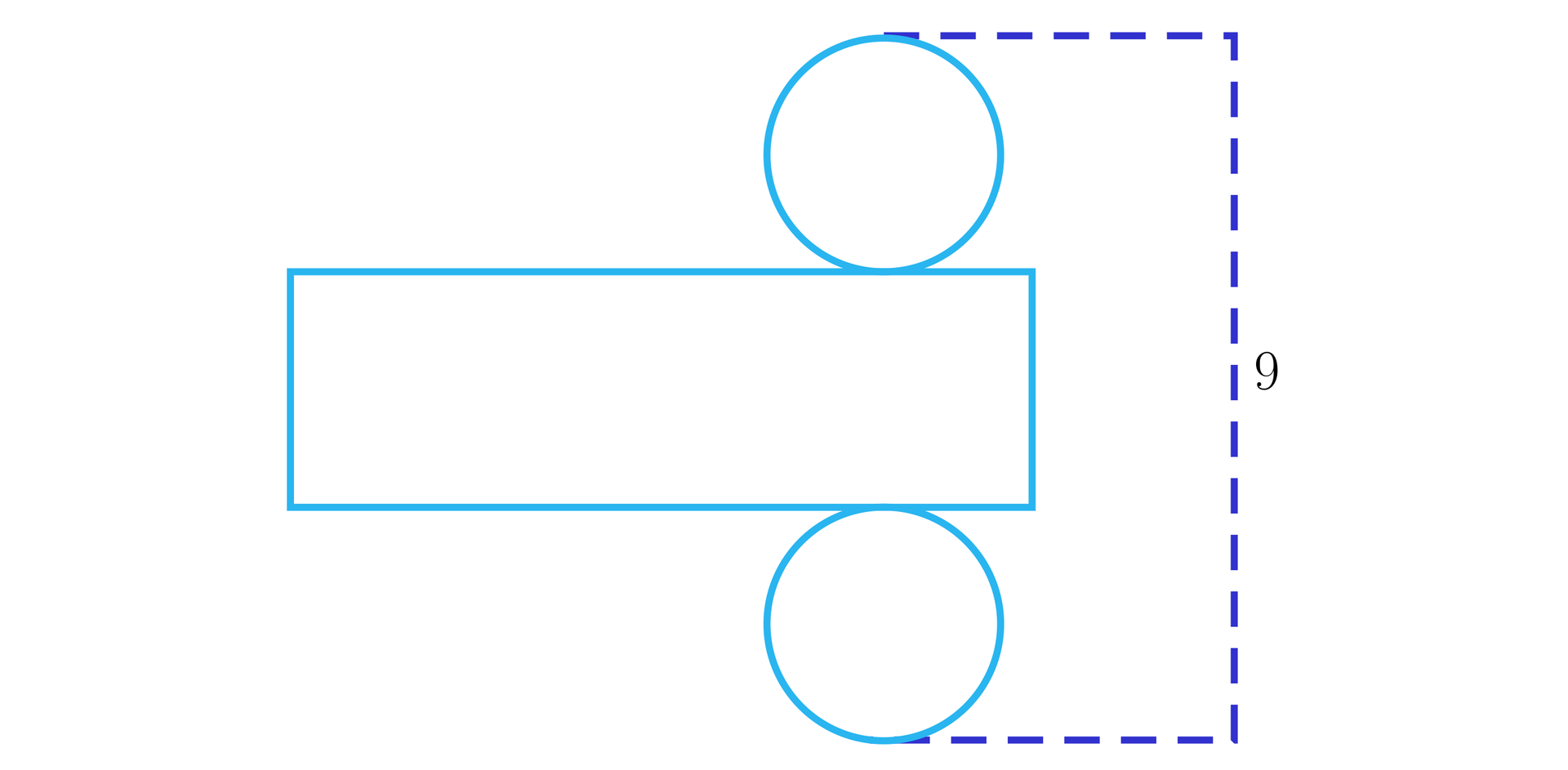
Ilustracja przedstawia siatkę walca składającą się z oraz dwóch kół stycznych do dłuższych przeciwległych boków prostokąta. Na ilustracji zaznaczony został także odcinek będący prostopadły do dłuższego boku prostokąta, łączący dwa krańcowe najbardziej oddalone od siebie punkty na obu okręgach. Odcinek ten ma długość dziewięć.

RQXh9S6A2iIip

Wybierz wszystkie zdania prawdziwe:

Średnica podstawy ma długość $3$ .
Dłuższy bok prostokąta będącego powierzchnią boczną walca ma długość $3 π$ .
Pole podstawy tego walca jest $4$ -krotnie mniejsze od pola prostokąta będącego powierzchnią boczną walca.
Dłuższy bok prostokąta będącego powierzchnią boczną walca ma długość $6 π$ .

R1cKuWkHxBvTD2

Ćwiczenie 6

W siatce walca o promieniu podstawy $r$ powierzchnia boczna jest kwadratem. Objętość tego walca wynosi wówczas:

$π r^{3}$
$2 π r^{2}$
$2 π^{2} r^{3}$
$2 π r^{2} + 4 π^{2} r^{2}$

Ćwiczenie 7

Promień podstawy jest $π$ -krotnie krótszy od wysokości walca, którego siatka znajduje się poniżej. Oblicz długość promienia podstawy i wysokość walca.

R1MvMgrA8NV0A

Powierzchnia boczna walca jest prostokątem o wymiarach $h \times 2 π r$ , a zatem biorąc pod uwagę dane z zadania: $π r \times 2 π r$ . Przekątna tego prostokąta ma długość $10$ .

Wyznaczymy $r$ z twierdzenia Pitagorasa: ${(π r)}^{2} + {(2 π r)}^{2} = 10^{2}$ . A zatem $r = \sqrt{\frac{100}{5 π^{2}}}$ i dalej $r = \frac{10 \sqrt{5}}{5 π} = \frac{2 \sqrt{5}}{π}$ . A to daje nam $h = r π = 2 \sqrt{5}$ .

$r = \frac{2 \sqrt{5}}{π}$

$h = 2 \sqrt{5}$

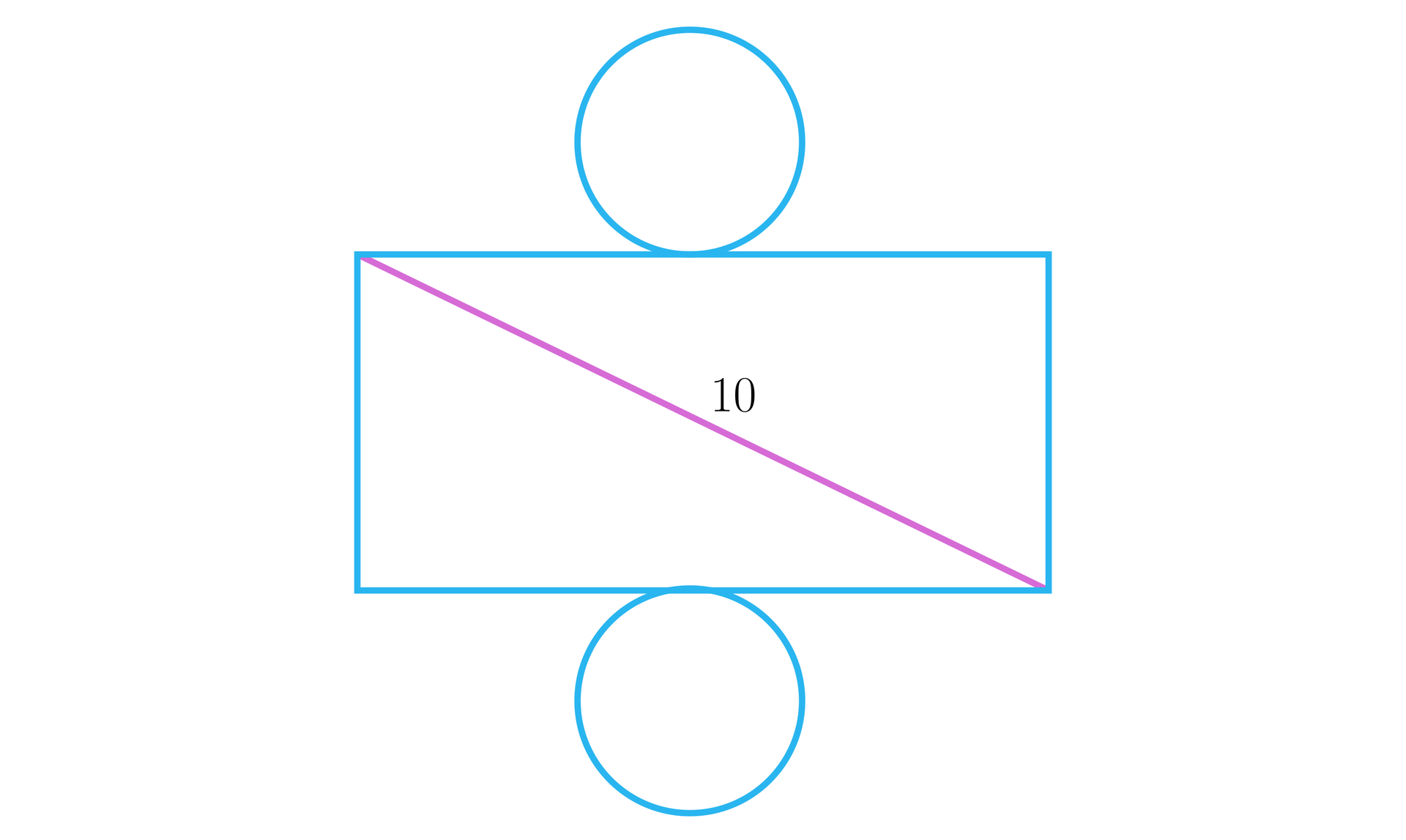
Ćwiczenie 8

Z siatki poniżej można zbudować walec. Długości przekątnych wynoszą odpowiednio $33, 4$ i $17, 6$ . Wysokość walca wynosi $4$ . Oblicz pole powierzchni tego walca. Przyjmij $π \approx 3, 14$ .

R45xU8irizlM5

Ilustracja przedstawia siatkę walca składającą się z równoległoboku oraz dwóch kół stycznych do dwóch dłuższych przeciwległych boków równoległoboku. Na ilustracji zaznaczono także dwie przekątne równoległoboku, a także kąt ostry alfa utworzony poprzez dwie przecinające się przekątne.

Obliczymy pole powierzchni bocznej tego walca ze wzoru: $P = \frac{1}{2} p q \sin α$ , gdzie $p$ , $q$ są przekątnymi równoległoboku będącymi przekątnymi tego walca, a $α$ kątem między nimi.

Mamy więc $P_{b} = \frac{1}{2} \cdot 33, 4 \cdot 17, 6 \cdot \sin 20 ° \approx 100, 52$ .

Obliczymy długość dłuższego boku równoległoboku ze wzoru na pole $P = a h$ . Stąd otrzymujemy $100, 52 = 4 a$ . A zatem $a = 25, 13$ . Oznaczmy przez $r$ promień podstawy tego walca. Otrzymujemy zatem $2 π r \approx 25, 13$ . Czyli $r \approx 4$ .

A zatem pole powierzchni tego walca wynosi około $P_{c} \approx 100, 52 + 2 \cdot 3, 14 \cdot 16 = 201$ .

Pole powierzchni $P_{c} \approx 201$ .

Aplet

Dla nauczyciela