Sprawdź się
Oblicz objętość ostrosłupa prawidłowego czworokątnego, jeśli jego przekrój pionowy jest trójkątem o podstawie o długości równej długości krawędzi kwadratowej podstawy bryły i trójkąt posiada wspólny górny wierzchołek z bryłą. Przekrój ma podstawę o długości i ramiona o długości każde.
Przyjrzyj się rysunkowi i uzupełnij zdania. Przeciągnij odpowiednie słowa.
Oblicz pole powierzchni ostrosłupa prawidłowego czworokątnego, jeżli jego przekrojem pionowym opartym na przekątnej kwadratowej podstawy jest trójkąt prostokątny równoramienny. Przekątna podstawy ma długość , wysokość bryły wynosi .
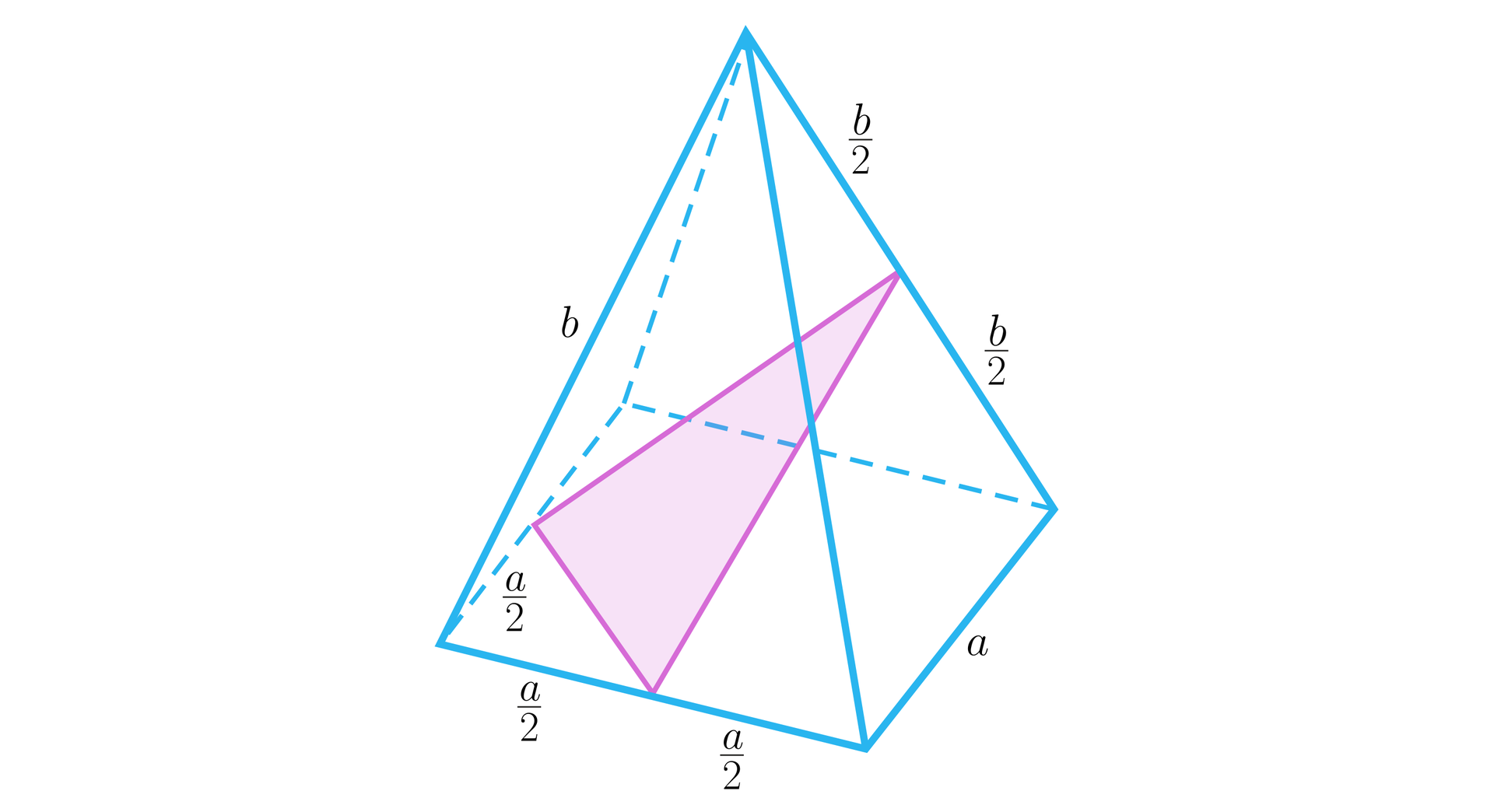
b. Przekrój ostrosłupa prawidłowego czworokątnego przechodzący przez środki krawędzi wychodzących z jednego wierzchołka podstawy jest 1. kwadratem, 2. trapezem, 3. trójkątem, 4. trójkątem, 5. kwadratem, 6. trapezem.
c. Przekrój ostrosłupa prawidłowego czworokątnego przechodzący przez krawędź podstawy i środki przeciwległych krawędzi bocznych jest 1. kwadratem, 2. trapezem, 3. trójkątem, 4. trójkątem, 5. kwadratem, 6. trapezem.
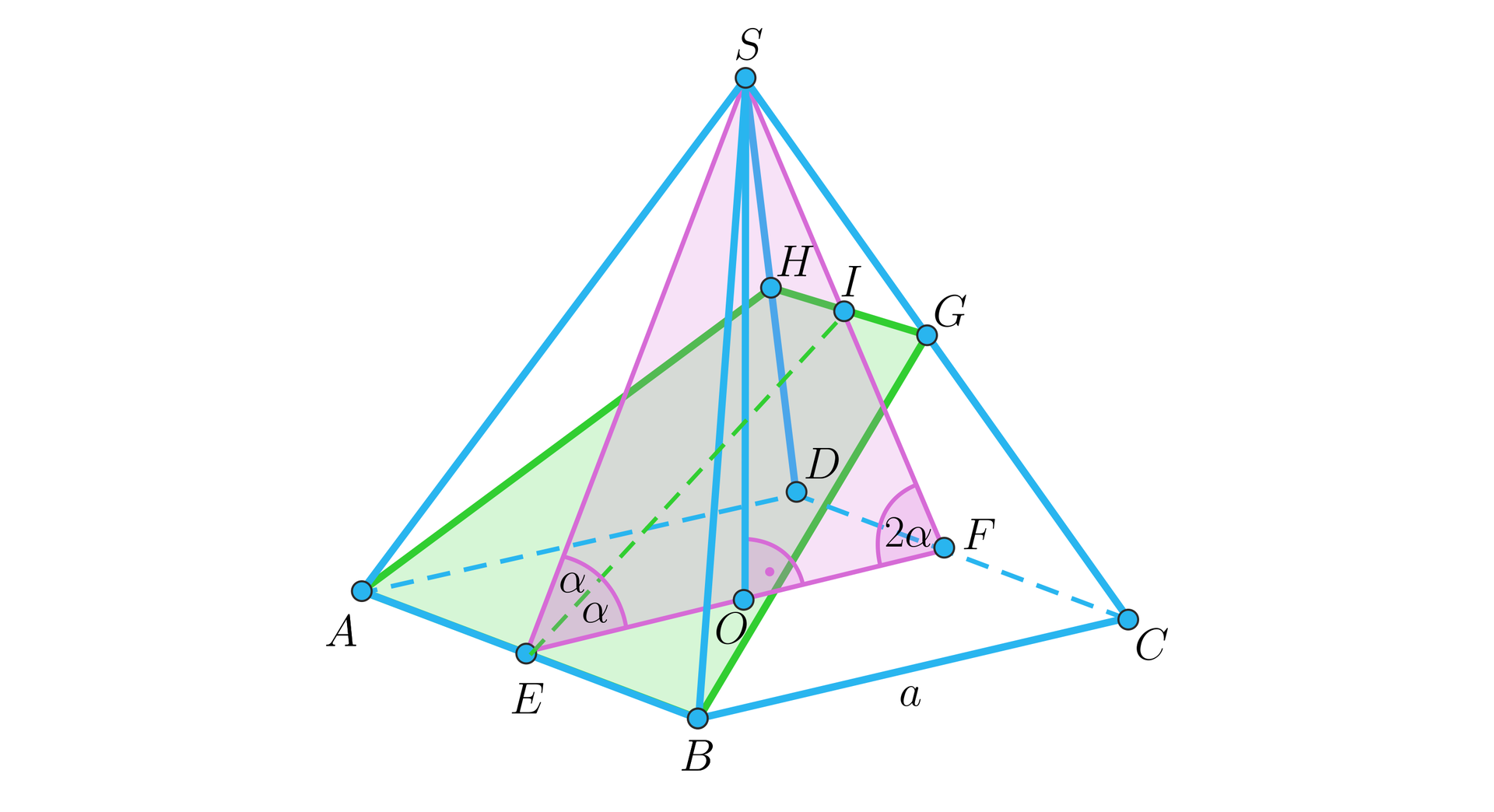
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem . Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.
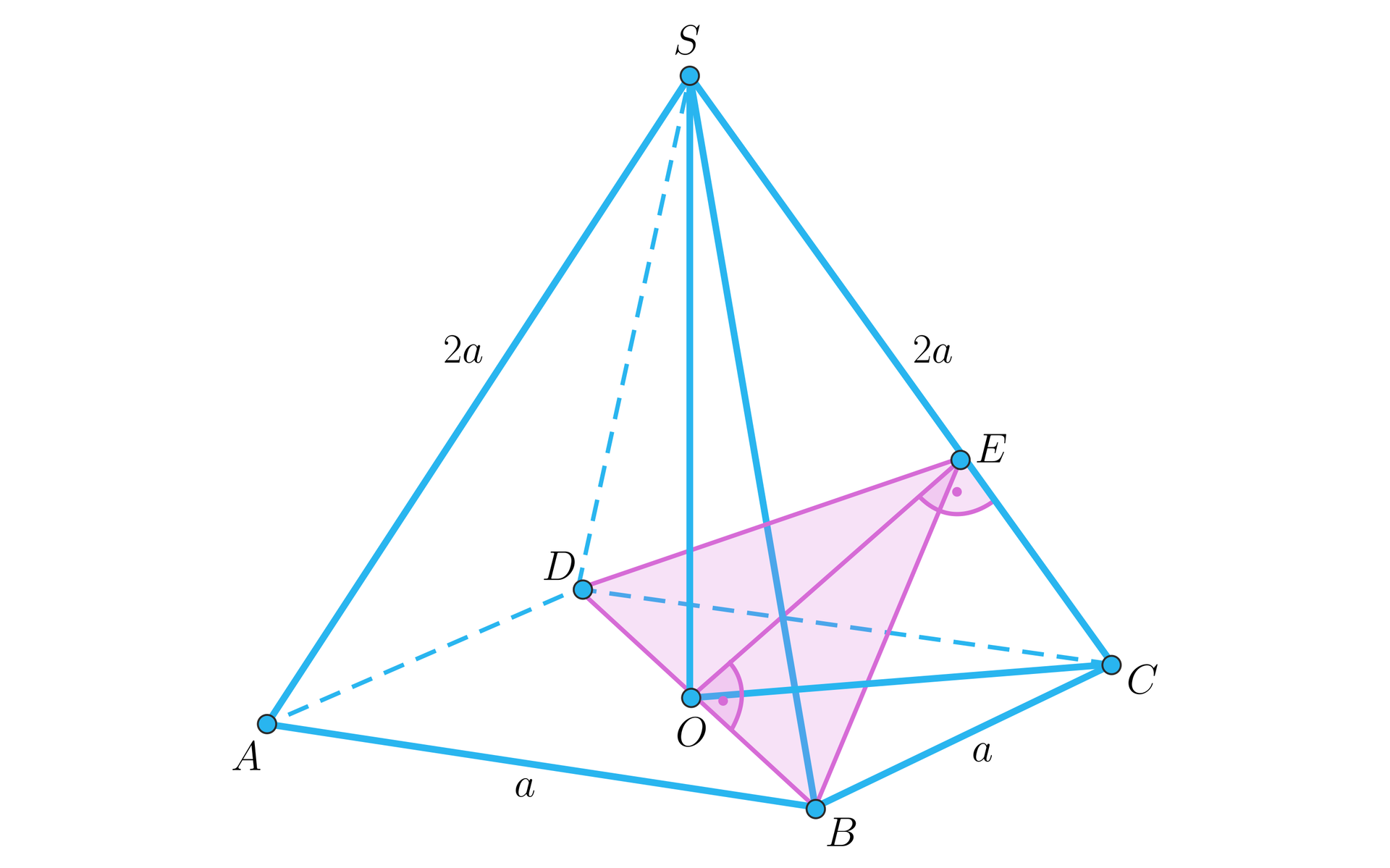
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość , zaś jego krawędź boczna jest dwa razy dłuższa. Wyznacz najmniejsze możliwe pole przekroju tego ostrosłupa płaszczyzną przechodzącą przez przekątną podstawy.