Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

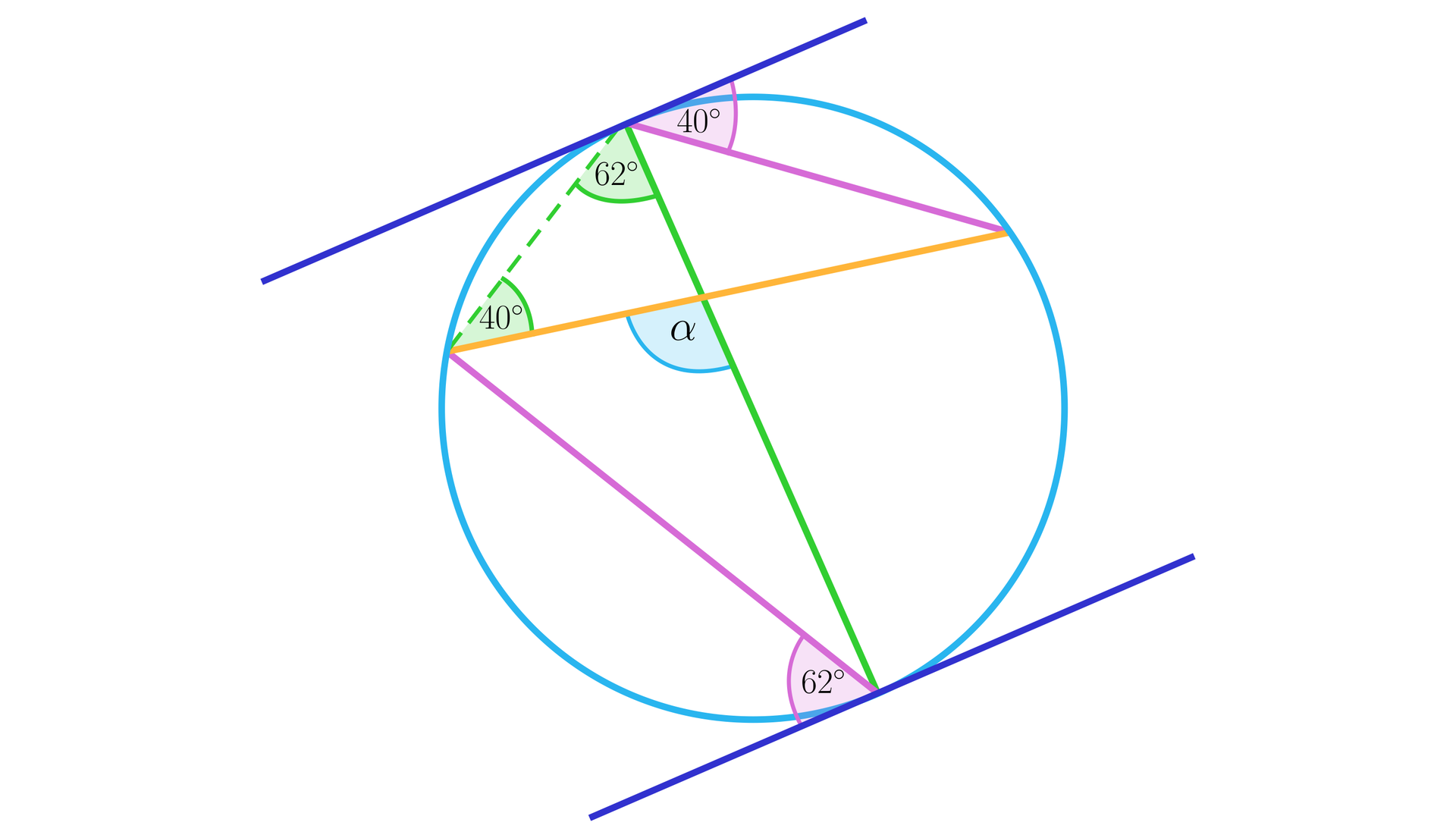
Na rysunku podane są miary dwóch kątów dopisanych. Wyznacz miarę kąta $α$ między odpowiednimi cięciwami tego okręgu.

R9jbHRcBFuR6B

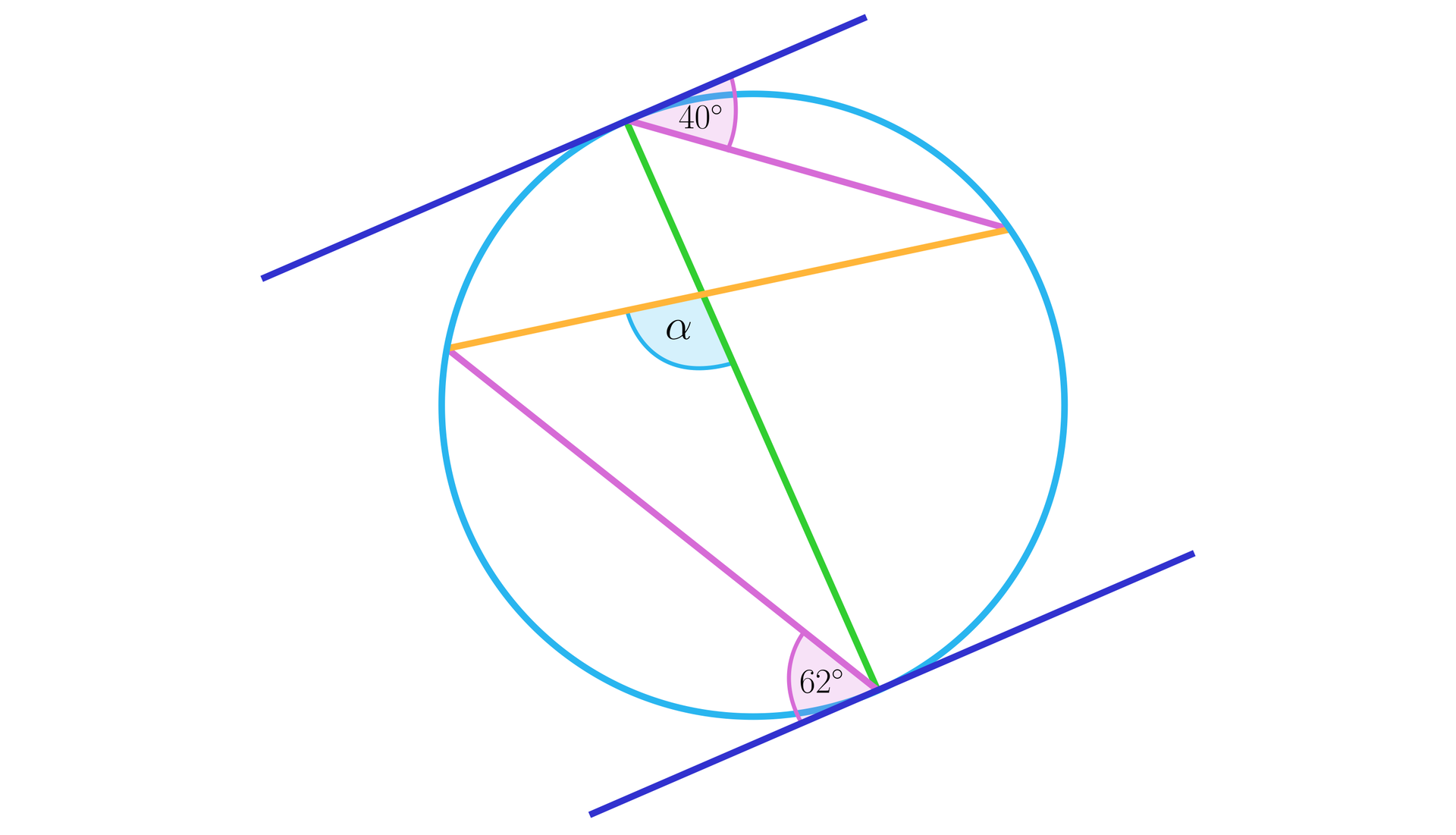
Ilustracja przedstawia okrąg wraz z jego dwiema stycznymi. Prosta leżąca powyżej jest nachylona do cięciwy A B krótszej od średnicy pod kątem 40 stopni. Prosta poniżej jest nachylona do cięciwy C D krótszej od średnicy pod kątem 62 stopni, przy czym druga z cięciw jest dłuższa. Proste połączono odcinkiem A D o końcach w punktach styczności. Odcinek ten przecięto czwartą cięciwą B C łączącą prawy koniec pierwszej cięciwy, czyli punkt B i lewy koniec drugiej cięciwy, czyli punkt C. Cięciwa B C przecina cięciwę A D w punkcie P. Zaznaczono kąt alfa będący kątem C P D.

Zaznaczmy na rysunku miary kątów, które są równe odpowiednim kątom dopisanym.

RQb2Qfq8gc9VF

Ilustracja przedstawia okrąg i dwie jego styczne z treści zadania. W okręgu wykreślono cięciwy A B, C D, A D oraz B C i zaznaczono szukany kąt alfa znajdujący się w przecięciu cięciw A D oraz B C, czyli kąt C P D, gdzie P jest punktem przecięcia cięciw. W rozwiązaniu dorysowano linią przerywaną cięciwę A C i oznaczono kąty: kąt C A P tożsamy z kątem C A D ma miarę 62 stopni. Kąt A C P tożsamy z kątem A C B ma miarę 40 stopni.

Wtedy kąt $α$ , jako kąt zewnętrzny w trójkącie, ma miarę $α = 40 ° + 62 ° = 102 °$ .

Ćwiczenie 2

Kąt, jaki tworzą sieczne, ma miarę równą $40 °$ , a zaznaczony na rysunku kąt dopisany ma miarę $30 °$ .

R1PpIT6UtAGf0

Ilustracja przedstawia okrąg i jego styczną w punkcie A. W okręgu wykreślono trzy cięciwy. Cięciwa A B krótsza od średnicy jest nachylona do stycznej pod kątem 30 stopni. Następnie mamy cięciwę B C krótszą od średnicy. Linią przerywaną narysowano cięciwę C A i oznaczono kąt ostry A C B jako alfa. Następnie narysowano cięciwę D A i kąt ostry D A C oznaczono jako beta. Linią przerywaną przedłużono cięciwy C B oraz D A w kierunku ich zwężania. Proste pokrywające cięciwy przecięły się pod kątem 40 stopni.

Oblicz miarę każdego z kątów $α$ i $β$ .

Z twierdzenia o kącie zewnętrznym w trójkącie wynika, że przy przyjętych oznaczeniach mamy: $β = α + 40 °$ .

Ale kąt $α$ jest równy mierze danego kąta dopisanego, stąd $α = 30 °$ oraz $β = 70 °$ .

Ćwiczenie 3

Dany jest okrąg opisany na trójkącie. Kąty trójkąta mają odpowiednio miary $α$ , $β$ oraz $γ$ , a miary wybranych kątów dopisanych, których wierzchołki pokrywają się z wierzchołkami trójkąta, są podane na rysunku. Jakie będą miary kątów $α$ i $β$ ?

RZQJGkryQ2pjS

Ilustracja przedstawia okrąg i trzy jego styczne. Punkty styczności wyznaczyły następujące cięciwy: A B, B C oraz C A. Styczne w punktach A i B są blisko siebie i przecinają się blisko okręgu. Styczna w punkcie C leży naprzeciw pozostałych stycznych. Na rysunku zaznaczono sześć kątów. Kąt między styczną w punkcie A i cięciwą A B wynosi 39 stopni, a kąt leżący obok niego i mający z nim wspólny wierzchołek, czyli kąt wpisany B A C oznaczono jako alfa. Kąt między prostą styczną w punkcie B i cięciwą B C wynosi 71 stopni, a kąt leżący obok niego i mający z nim wspólny wierzchołek, czyli kąt C B A oznaczono jako beta. Kąt między styczną w punkcie C i cięciwą C A wynosi 70 stopni, a kąt leżący obok niego, mający z nim wspólny wierzchołek, czyli kąt A C B oznaczono jako gamma.

Rwa7kNbSyn1xg

Ćwiczenie 4

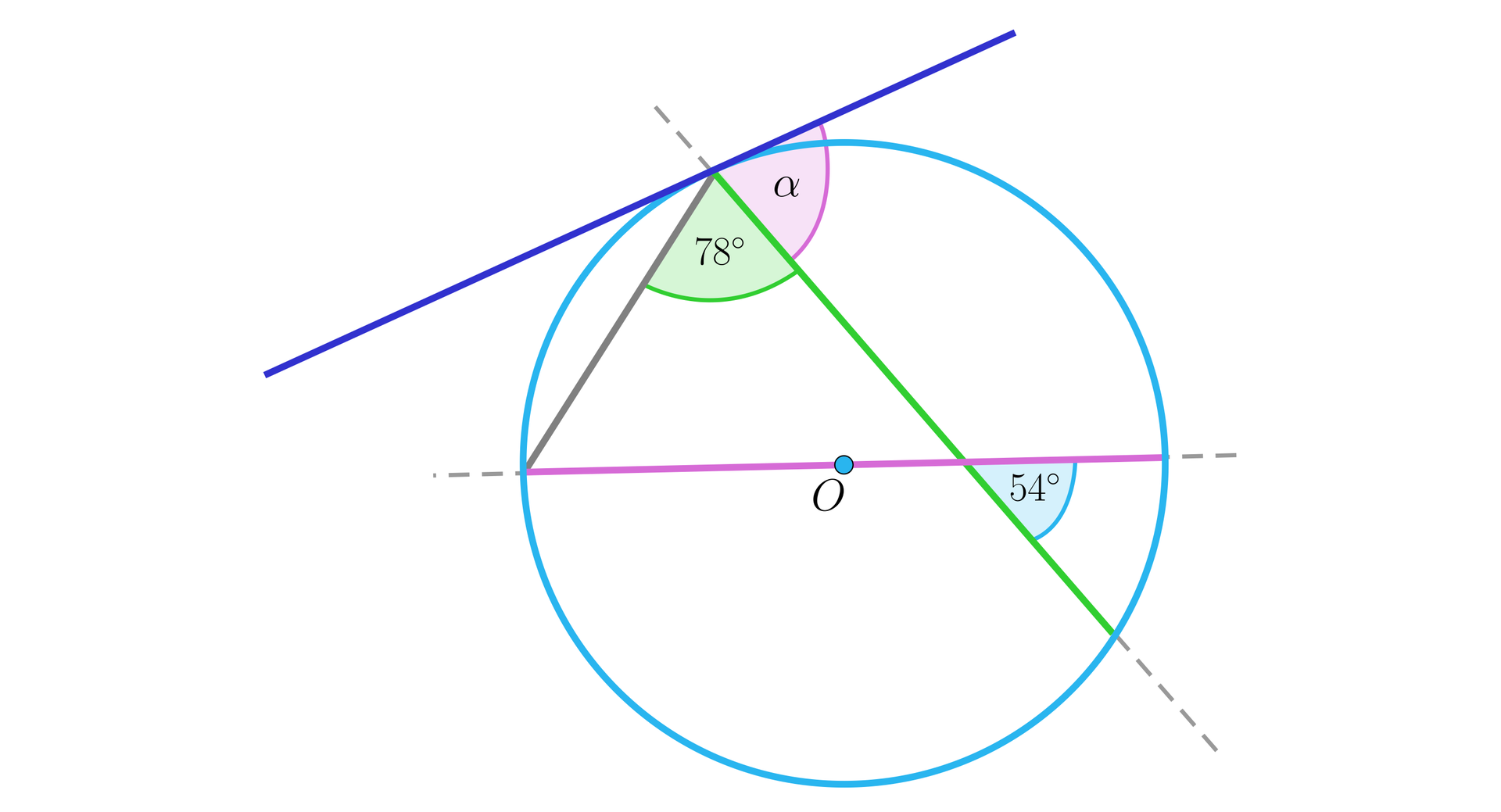
Sieczne danego okręgu przecinają się pod kątem $54 °$ . Kąt wpisany, którego wierzchołek pokrywa się z wierzchołkiem kąta dopisanego ma miarę $78 °$ , jak na rysunku. Jaką miarę ma kąt dopisany $α$ ?

R18W4iMcGpPjQ

Ilustracja przedstawia okrąg o środku w punkcie O. Zaznaczono średnicę A B okręgu oraz dwie cięciwy o wspólnym końcu: cięciwę A C oraz C D. Cięciwa C D jest dłuższa i przecina się ze średnicą A B w punkcie P pod kątem 4 stopnie. Kąt między styczną w punkcie C a cięciwą C D to kąt ostry alfa. Kąt wpisany A C D ma miarę 78 stopni.

RGYtI4iaNWoFW

Ćwiczenie 5

RGsKEt5yuZqrM

R1I6YA2gwVR7y

Ćwiczenie 6

W danym okręgu poprowadzono cięciwę, której końce podzieliły okrąg na dwa łuki. Stosunek długości tych łuków ma się do siebie tak, jak $3 : 5$ . Oblicz miary kątów dopisanych, których wierzchołkami są końce poprowadzonej cięciwy.

Zauważmy, że stosunek miar kątów środkowych opartych na danej cięciwie ma się tak, jak $3 : 5$ .

Zatem kąty te mają miary odpowiednio równe $135 °$ oraz $225 °$ .

Kąty dopisane mają miary dwa razy mniejsze, zatem są one odpowiednio równe $67 ° 30'$ oraz $112 ° 30'$ .

Uwaga:

Łatwo zauważyć, że kąty dopisane o wierzchołkach w końcach danej cięciwy są sobie odpowiednio równe.

Ćwiczenie 7

Dłuższy bok prostokąta $A B C D$ jest średnicą okręgu o promieniu $r$ , jak na rysunku.

RVqC2NZM0ULSc

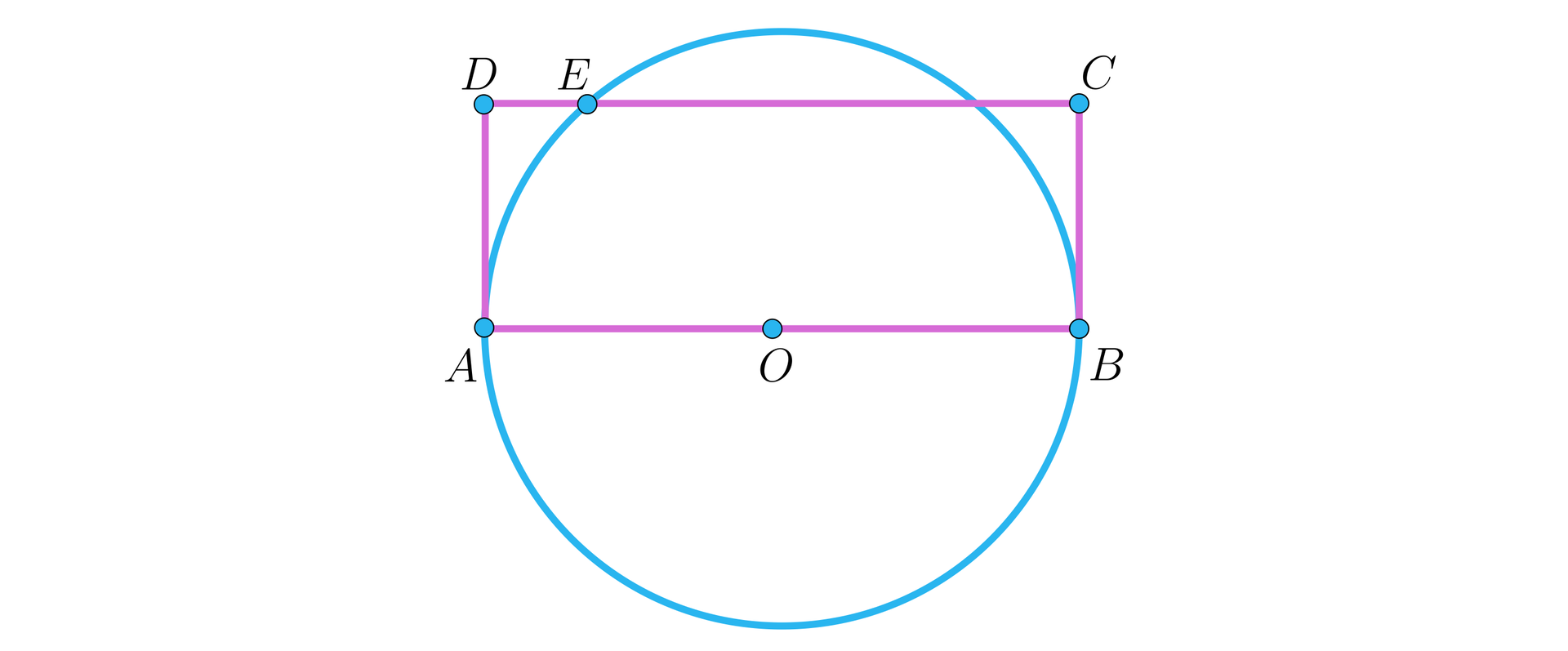
Ilustracja przedstawia okrąg o środku w punkcie O i prostokąt A B C D, którego dłuższy bok A B jest średnicą okręgu. Prostokąt narysowany jest w obrębie górnego półokręgu. Jego krótszy pionowy bok jest krótszy od promienia okręgu, zatem jego górna podstawa przecina górny półokrąg w dwóch punktach, przy czym lewy z tych punktów wyróżniono i opisano literą E.

Prosta $C D$ przecięła okrąg w takim punkcie $E$ , że $|D E| = \frac{1}{3} r$ . Wyznacz stosunek długości boków tego prostokąta.

Poprowadźmy odcinki $A E$ i $B E$ , jak na rysunku.

RrQMr0AoEUGp8

Ilustracja przedstawia okrąg o środku w punkcie O oraz prostokąt A B C D, którego dłuższy bok A B jest średnicą okręgu. Jego krótszy bok jest krótszy od promienia, zatem jego górna podstawa C D przecina górny półokrąg w dwóch punktach, przy czym lewy opisano literą E. Narysowano kąt wpisany oparty na średnicy A B. Kąt ten to A E B.

Wtedy kąt $A E B$ jest prosty i kąt dopisany $E A D$ jest równy kątowi $A B E$ .

Ponieważ $tg (∢ E A D) = \frac{\frac{1}{3} r}{|A D|}$ oraz $tg (∢ A B E) = \frac{|A D|}{2 r - \frac{1}{3} r} = \frac{|A D|}{\frac{5}{3} r}$ , więc $\frac{|A D|}{\frac{5}{3} r} = \frac{\frac{1}{3} r}{|A D|}$ .

Stąd ${|A D|}^{2} = \frac{5}{9} r^{2}$ .

Zatem $\frac{|A B|}{|A D|} = \frac{2 r}{\frac{\sqrt{5}}{3} r} = \frac{6}{\sqrt{5}}$ .

Ćwiczenie 8

R4cruFtMbU1hY

Aplet

Dla nauczyciela