Sprawdź się
Oceń prawdziwość zdań
| Zdanie | Prawda | Fałsz |
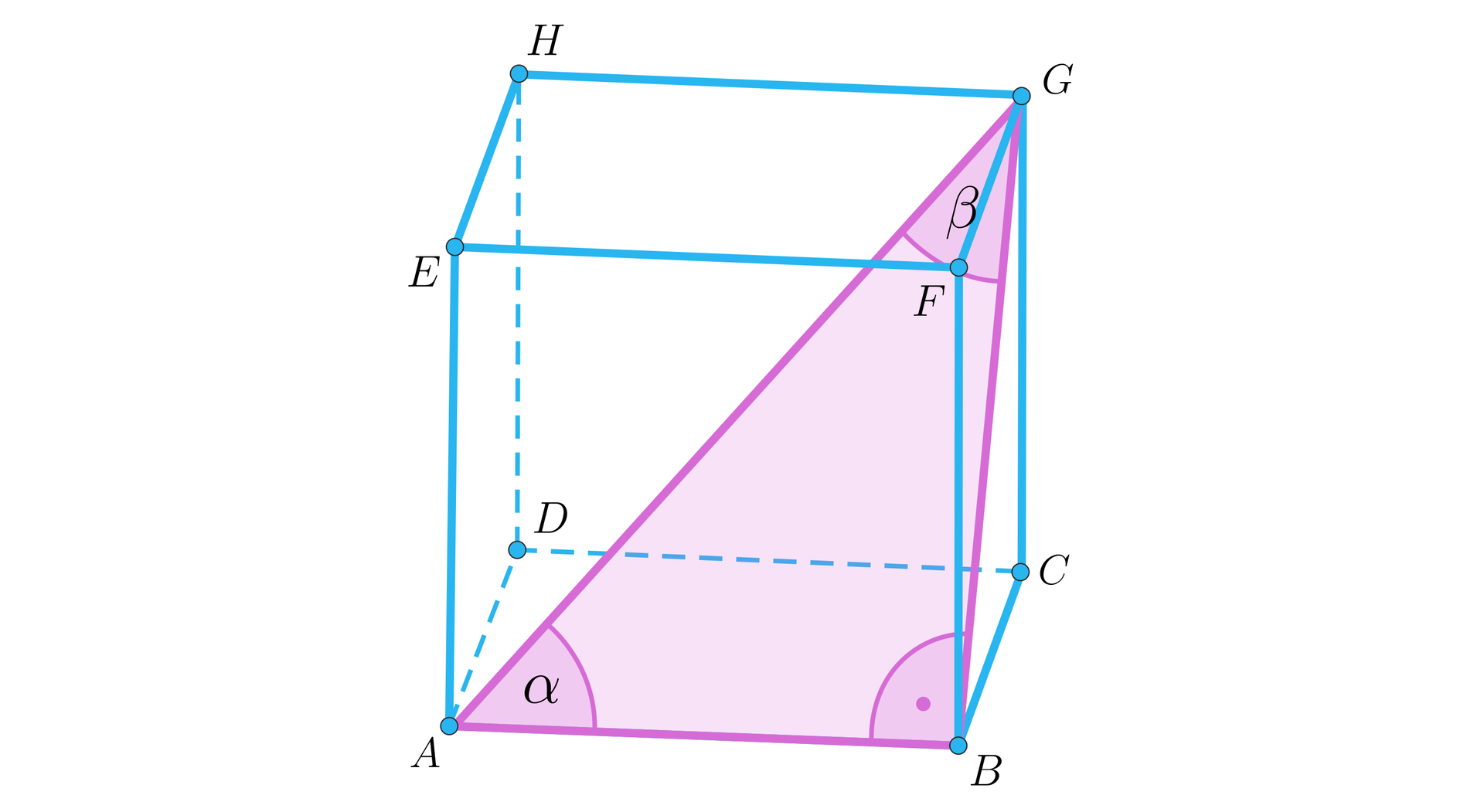
| Kąt pomiędzy przekątnymi sąsiednich ścian sześcianu wychodzącymi ze wspólnego wierzchołka ma miarę . | □ | □ |
| Kąt nachylenia przekątnej ściany do płaszczyzny sąsiedniej ściany to kąt pomiędzy przekątnymi sąsiednich ścian. | □ | □ |
| Zmiana długości krawędzi sześcianu nie wpływa na miarę kąta pomiędzy przekątnymi sześcianu. | □ | □ |
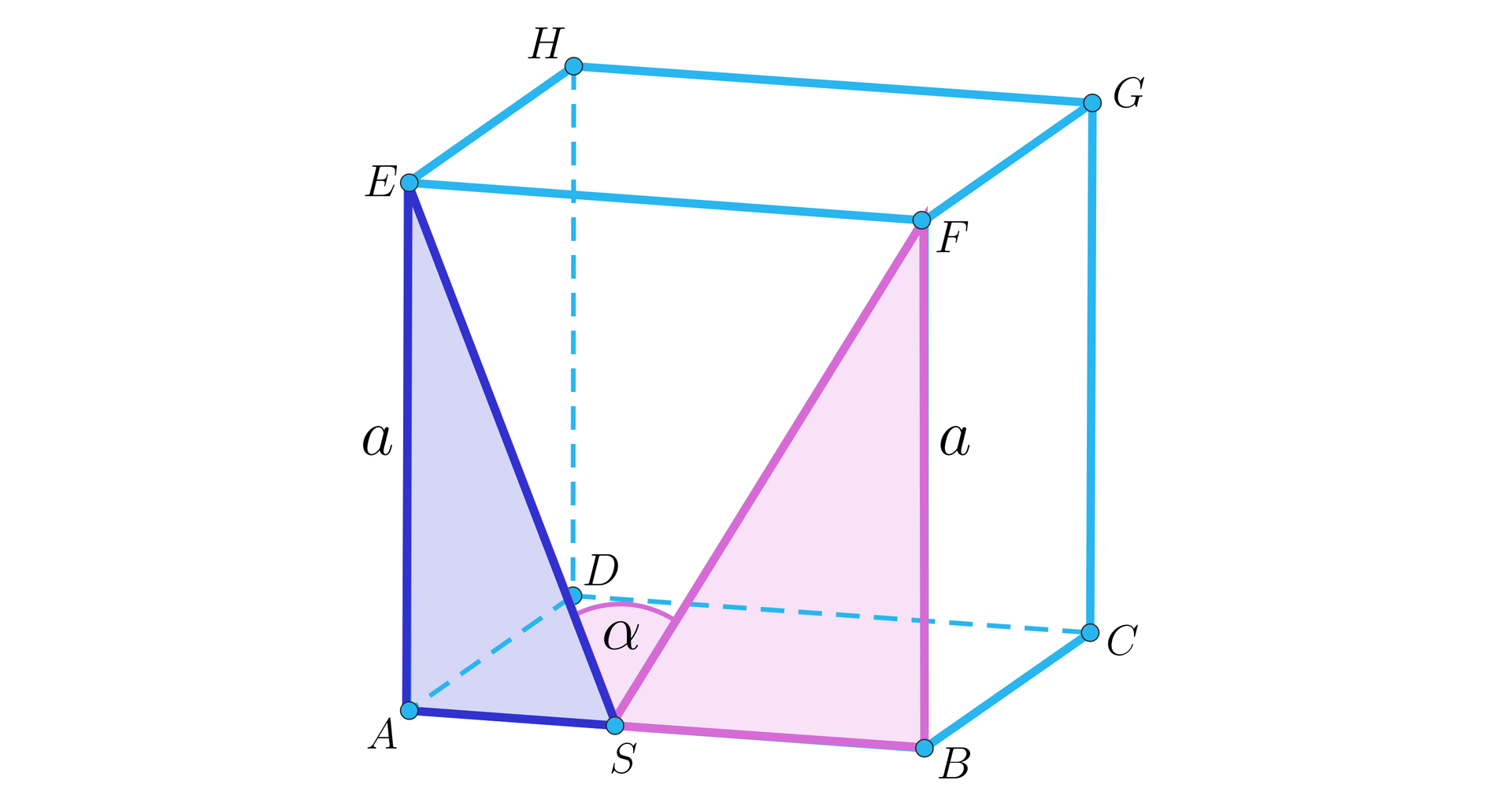
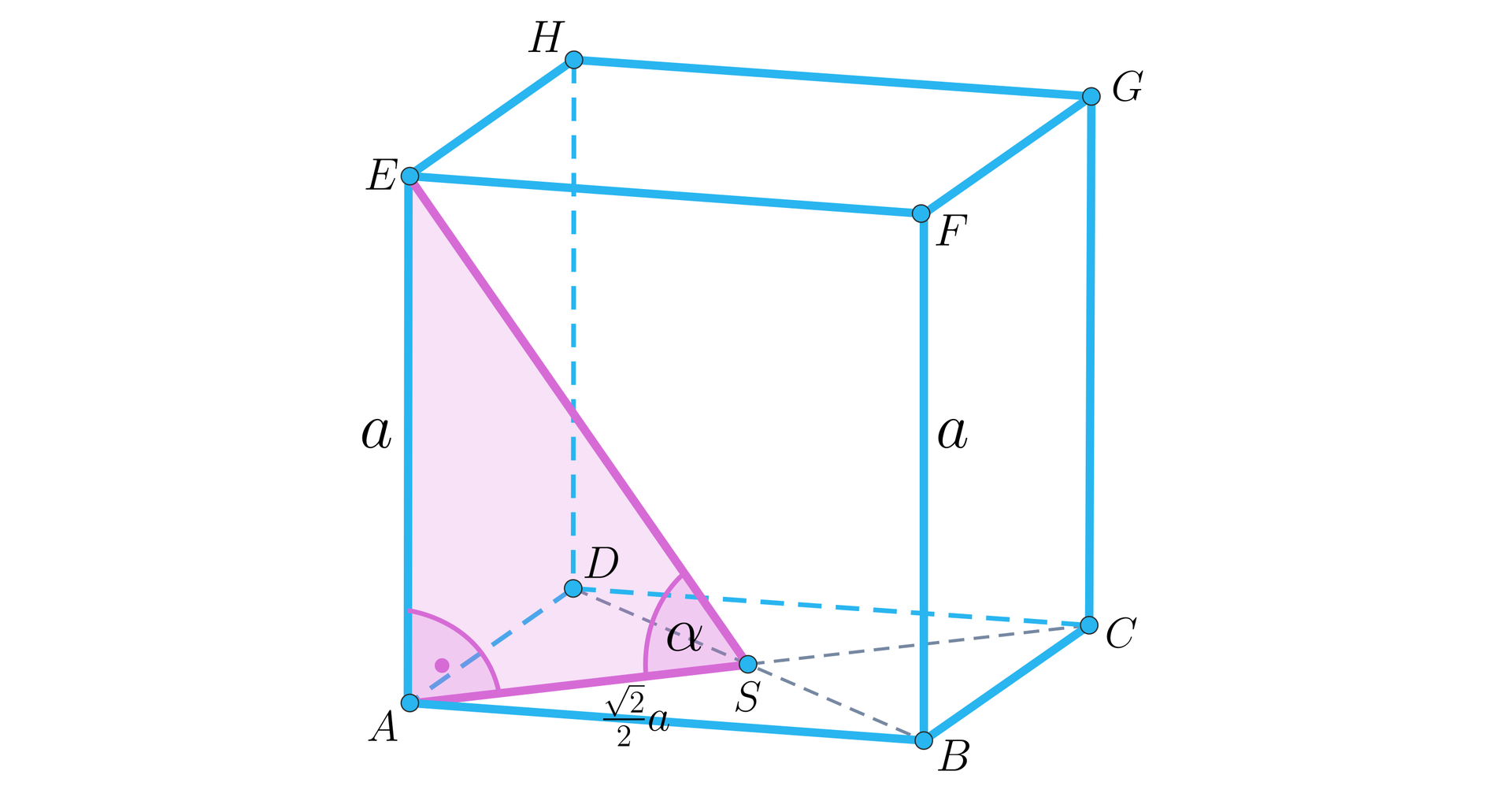
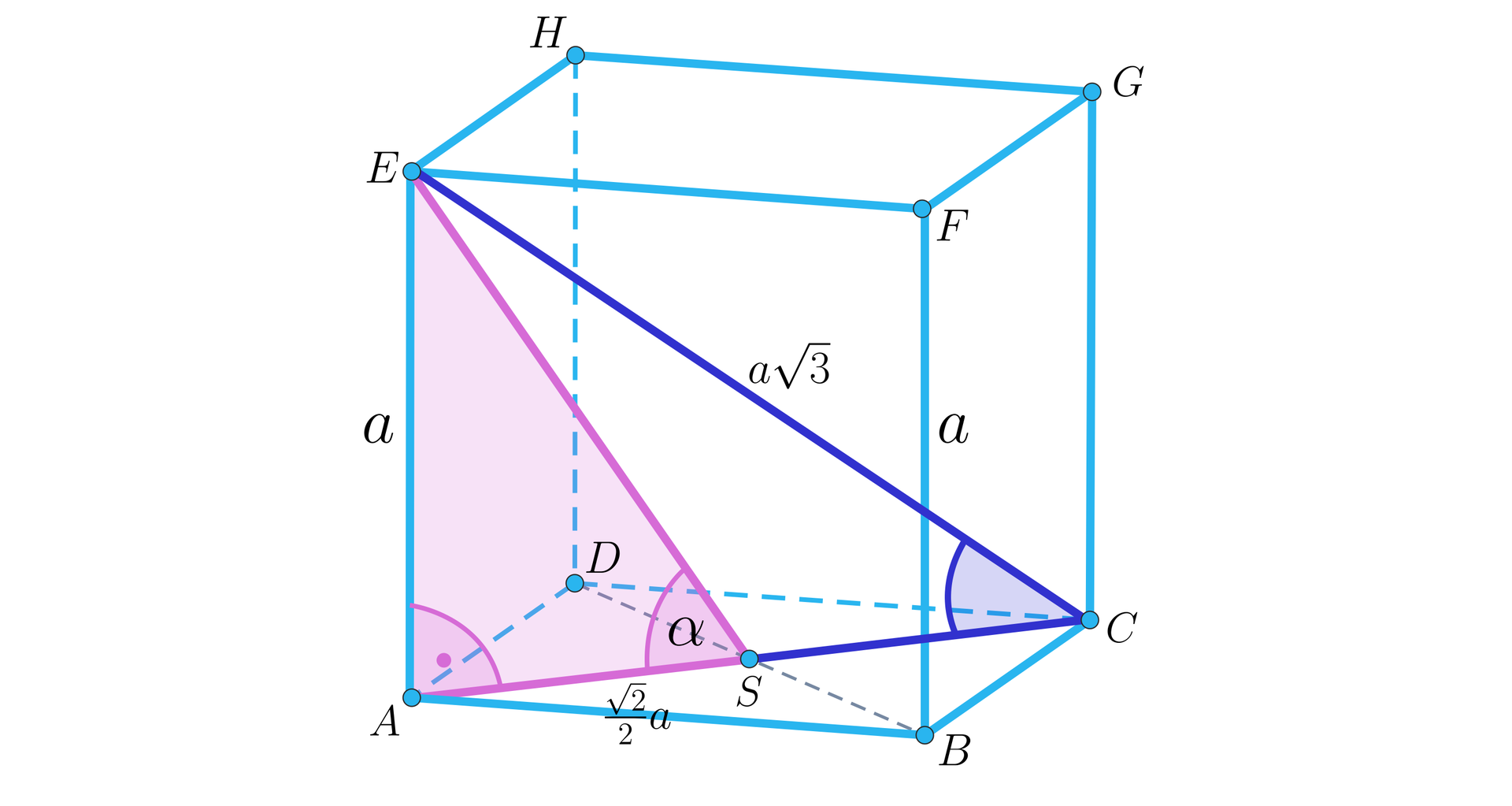
Wskaż wartość tangensa kąta między przekątną sześcianu a krawędzią sześcianu:
Wskaż wartość cosinusa kąta ostrego wyznaczonego przez przekątne sześcianu:
- Kąt pomiędzy przekątną sześcianu a krawędzią sześcianu ma miarę 1. mniejszą, 2. mniejszą, 3. większą, 4. mniejszą, 5. większą, 6. większą niż .
- Kąt nachylenia przekątnej sześcianu do podstawy ma miarę 1. mniejszą, 2. mniejszą, 3. większą, 4. mniejszą, 5. większą, 6. większą niż .
- Kąt ostry pomiędzy przekątnymi sześcianu ma miarę 1. mniejszą, 2. mniejszą, 3. większą, 4. mniejszą, 5. większą, 6. większą niż .
Uzupełnij zdania przeciągając odpowiednie słowo.
mniejszą, mniejszą, większą, większą, większą, mniejszą
1. Kąt pomiędzy przekątną sześcianu, a krawędzią sześcianu ma miarę .................. niż .
2. Kąt nachylenia przekątnej sześcianu do podstawy ma miarę .................. niż .
3. Kąt ostry pomiędzy przekątnymi sześcianu ma miarę .................. niż .
Uzasadnij, nie wykonując obliczeń, że sinus kąta nachylenia przekątnej sześcianu do jego ściany jest równy cosinusowi kąta pomiędzy przekątną sześcianu a jego krawędzią.
Punkt dzieli krawędź w stosunku .
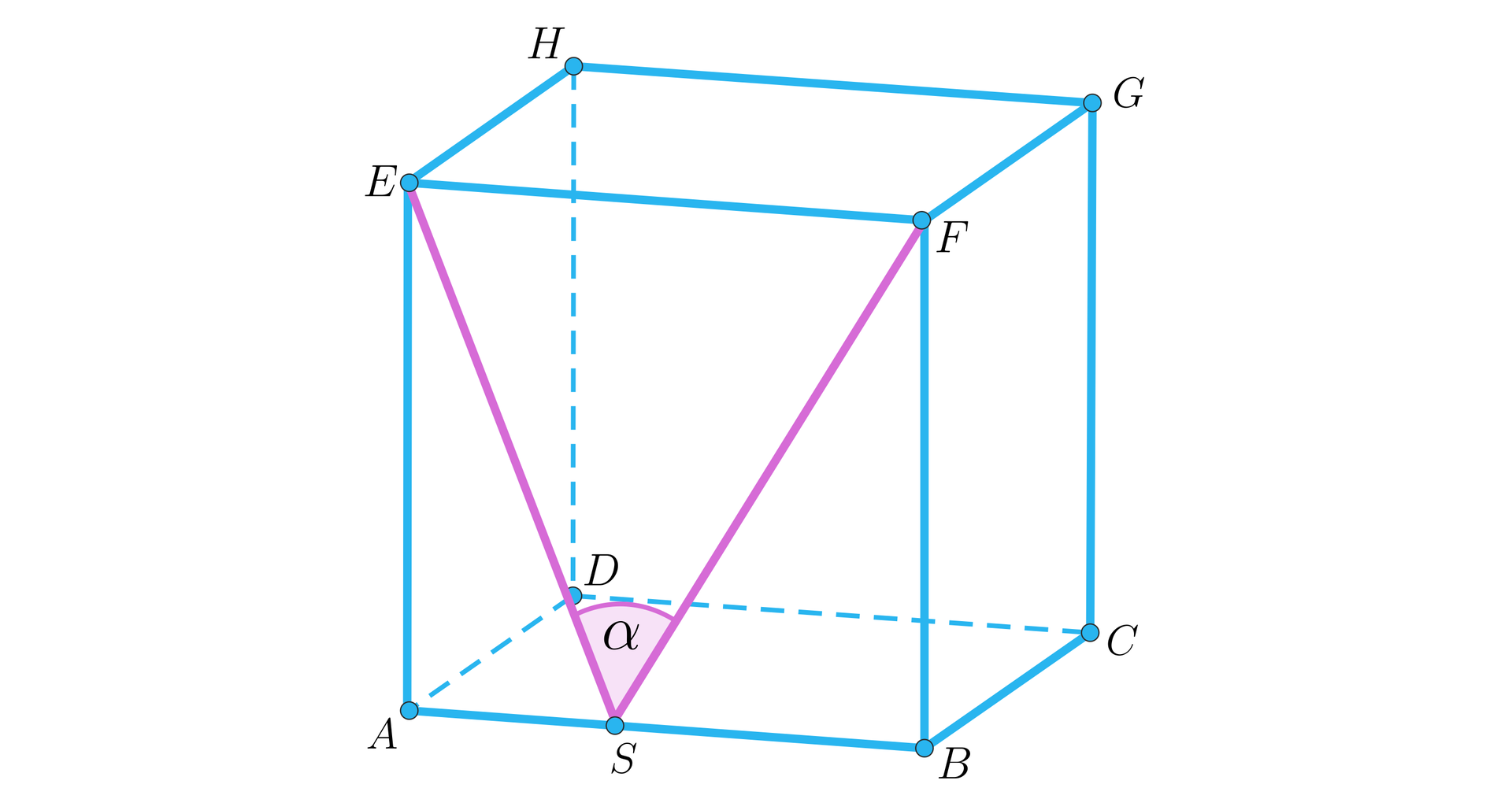
Ile wynosi cosinus kąta pomiędzy odcinkami i ?
Punkt jest punktem przecięcia przekątnych w podstawie sześcianu jak na rysunku.
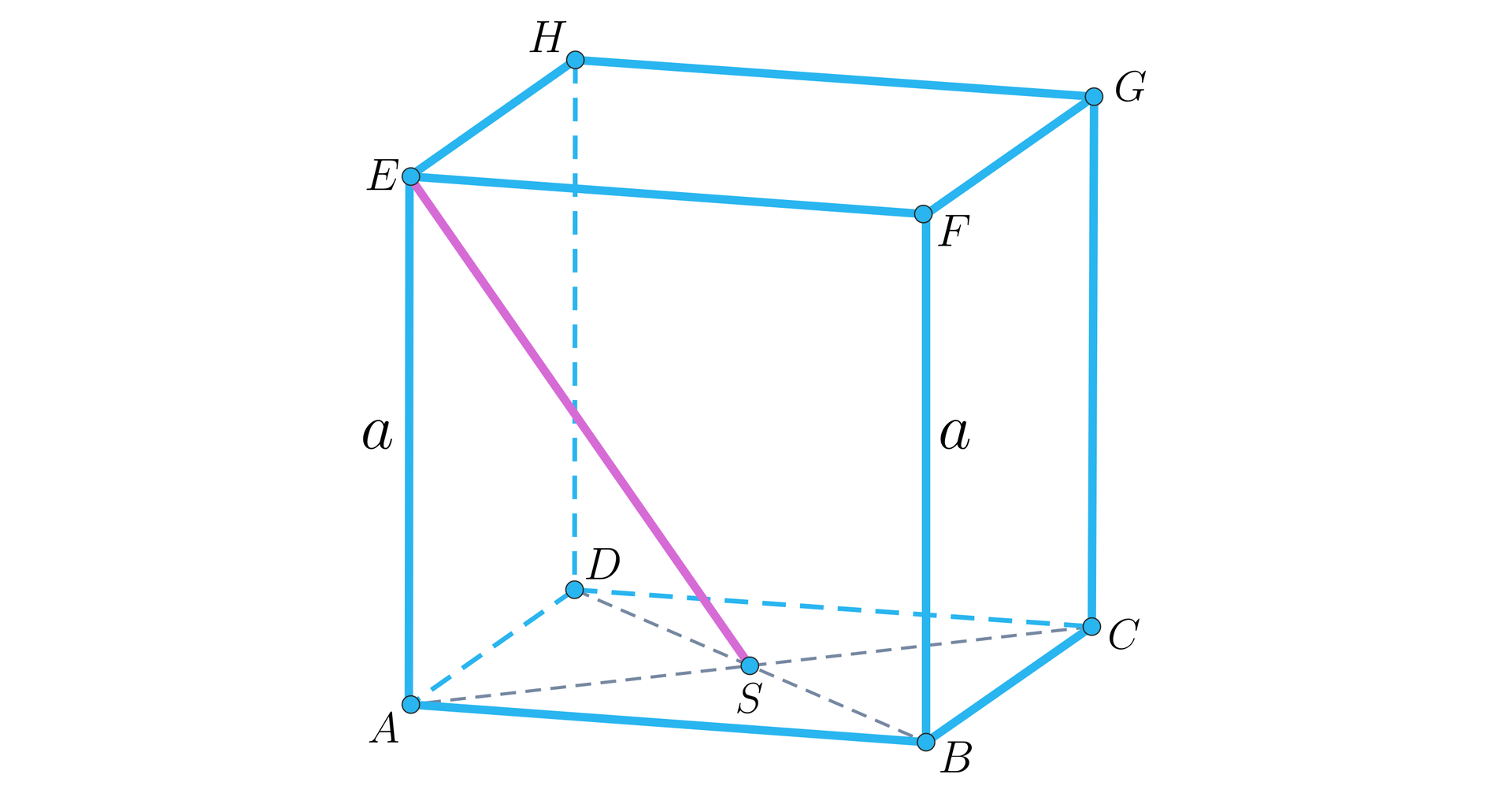
Oblicz cosinus kąta jaki odcinek tworzy z płaszczyzną podstawy.
Uzasadnij, że kąt ma tę samą miarę, co kąt nachylenia przekątnej sześcianu do płaszczyzny podstawy.