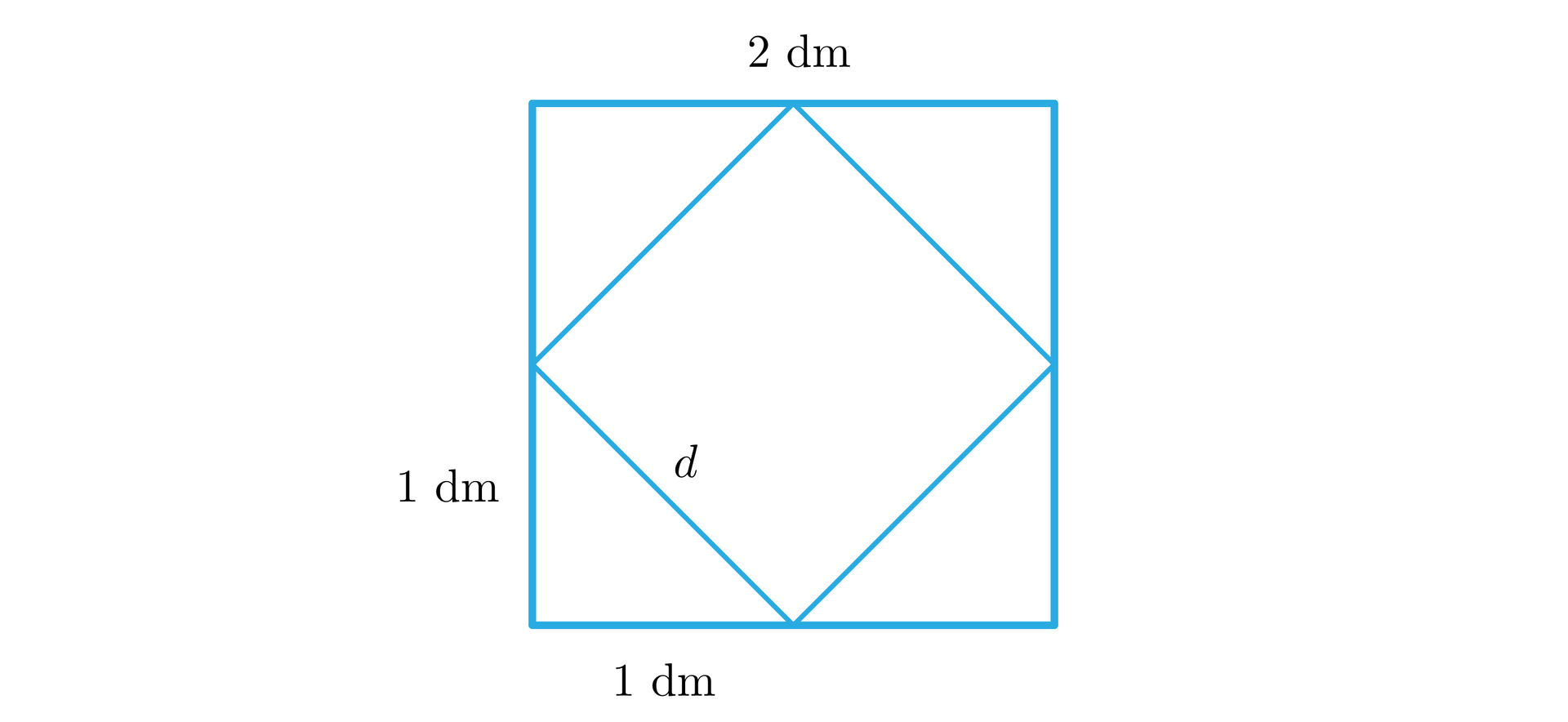
Sprawdź się
Uzupełnij tabelę.
| Nazwa | Liczba wierzchołków | Liczba krawędzi | Liczba ścian |
|---|---|---|---|
| Czworościan ścięty | |||
| Sześcian ścięty | |||
| Dwunastościan ścięty |
Do każdej z podanych brył dopasuj opis jej ścian.
Dwudziesto – dwunastościan, Sześcian ścięty, Czworościan ścięty, Ośmiościan ścięty
| Nazwa bryły | Ściany |
|---|---|
| Dwudziesto – dwunastościan | |
| Sześcian ścięty | |
| Czworościan ścięty | |
| Ośmiościan ścięty |
Z sześcianu o krawędzi odcięto narożniki prowadząc cięcia przez środki krawędzi sześcianu. Otrzymano w ten sposób sześcio – ośmiościan. Oblicz sumę długości wszystkich krawędzi tego sześcio – ośmiościanu.
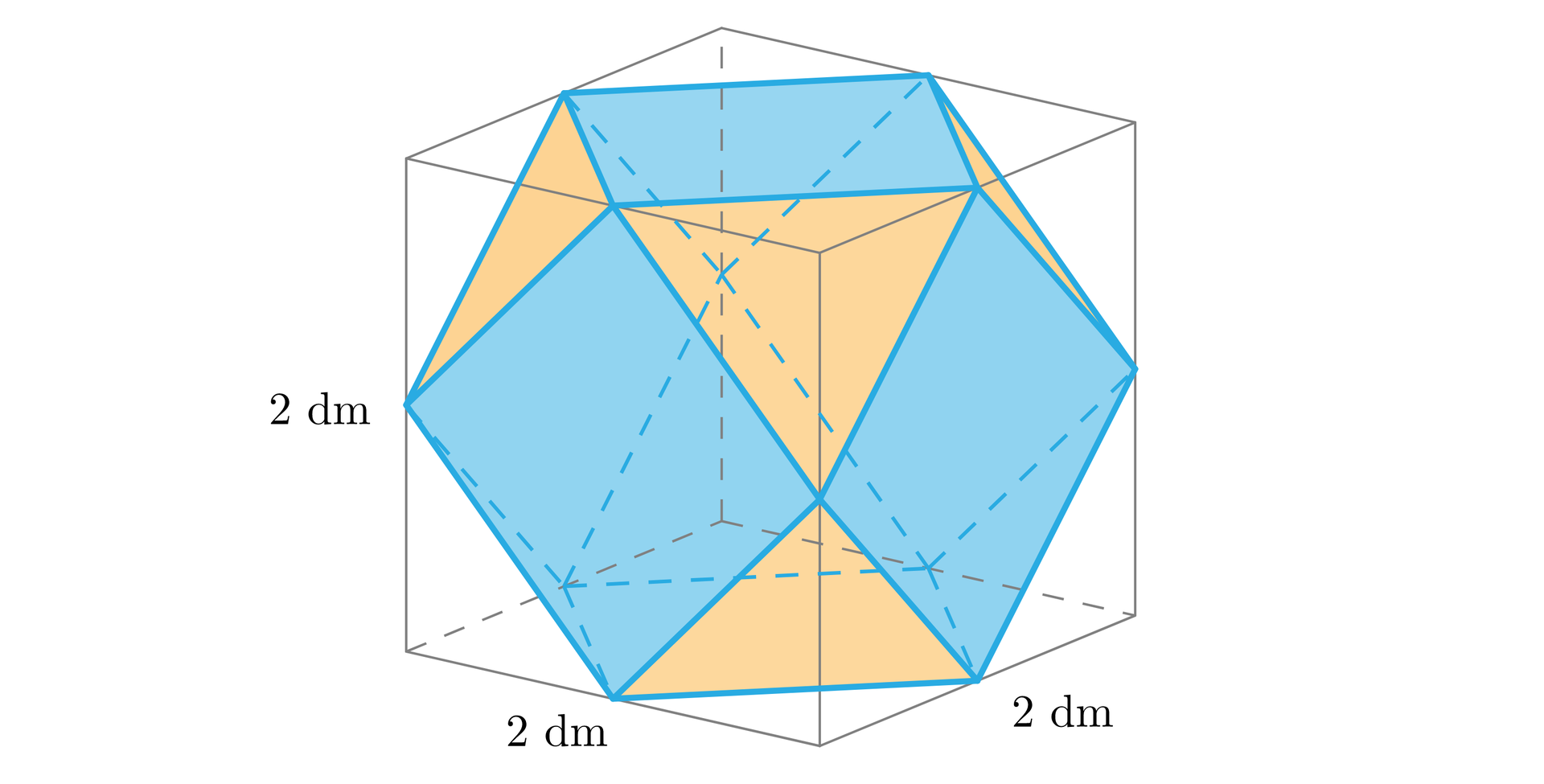
Z sześcianu o krawędzi odcięto narożniki prowadząc cięcia przez środki krawędzi sześcianu. Otrzymano w ten sposób sześcio – ośmiościan. Oblicz pole powierzchni całkowitej tego sześcio – ośmiościanu.

Z sześcianu o krawędzi odcięto narożniki prowadząc cięcia przez punkty dzielące krawędzie na równe części. Otrzymano w ten sposób sześcian ścięty.
Oblicz, o ile objętość powstałej bryły jest mniejsza od objętości sześcianu.
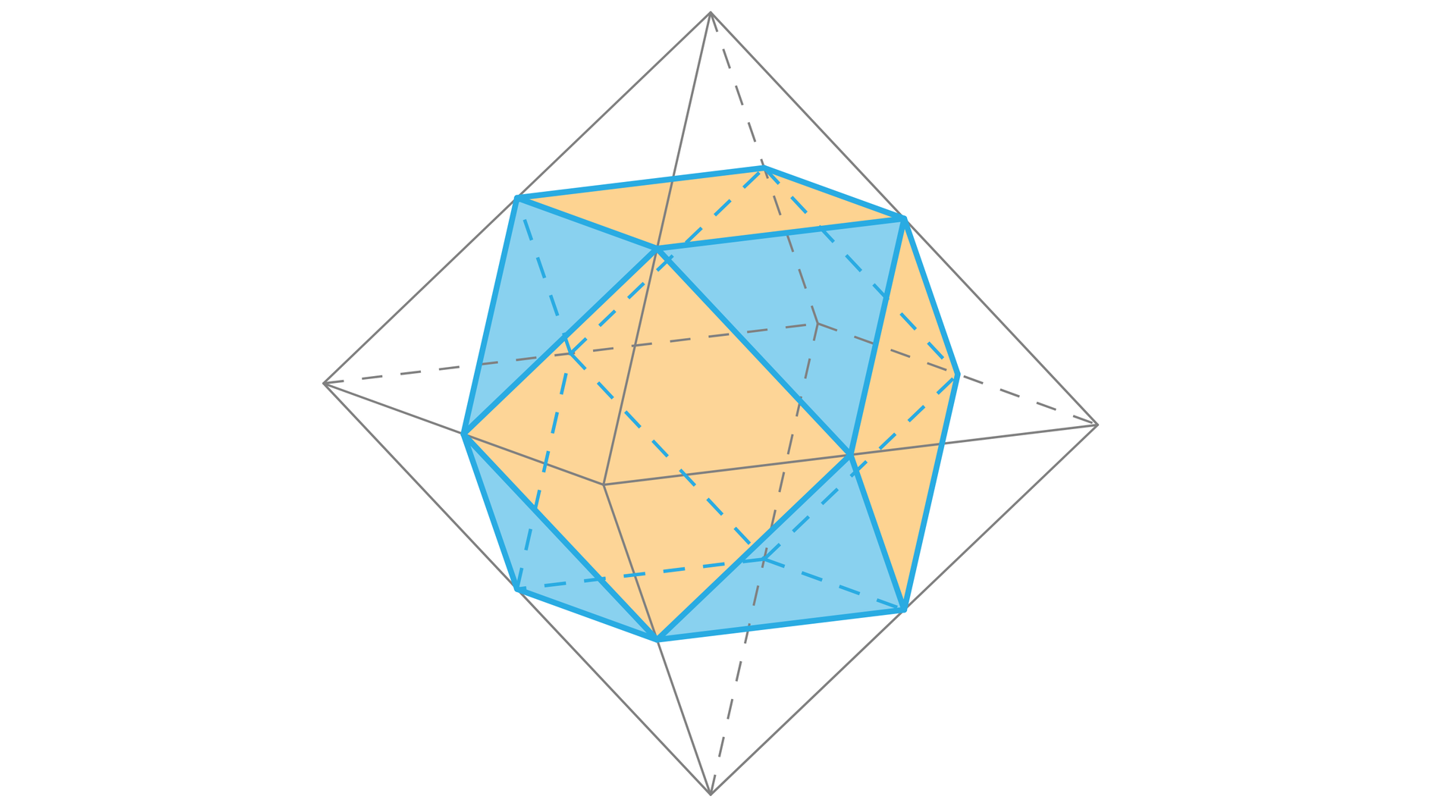
W drewnianym klocku w kształcie ośmiościanu foremnego odcinamy naroża prowadząc cięcia przez środki krawędzi. Otrzymujemy w ten sposób sześcio – ośmiościan. Jaki procent objętości ośmiościanu stanowi objętość tego sześcio – ośmiościanu?
Z ośmiościanu foremnego o krawędzi długości odcinamy naroża tak, że wszystkie krawędzie otrzymanej bryły mają jednakową długość, a jej ściany są wielokątami foremnymi tak, jak na rysunku (ośmiościan ścięty). Oblicz objętość tej bryły.