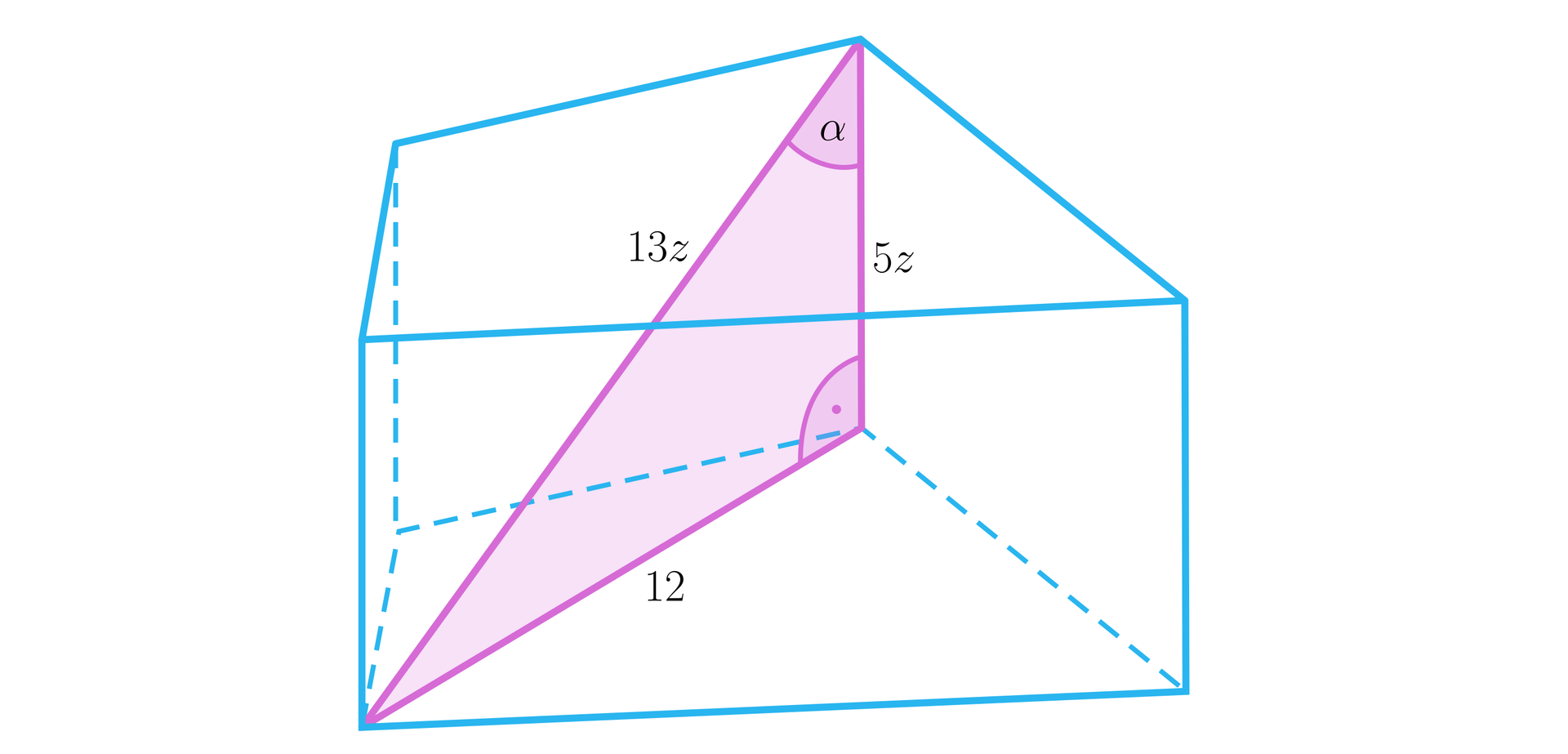
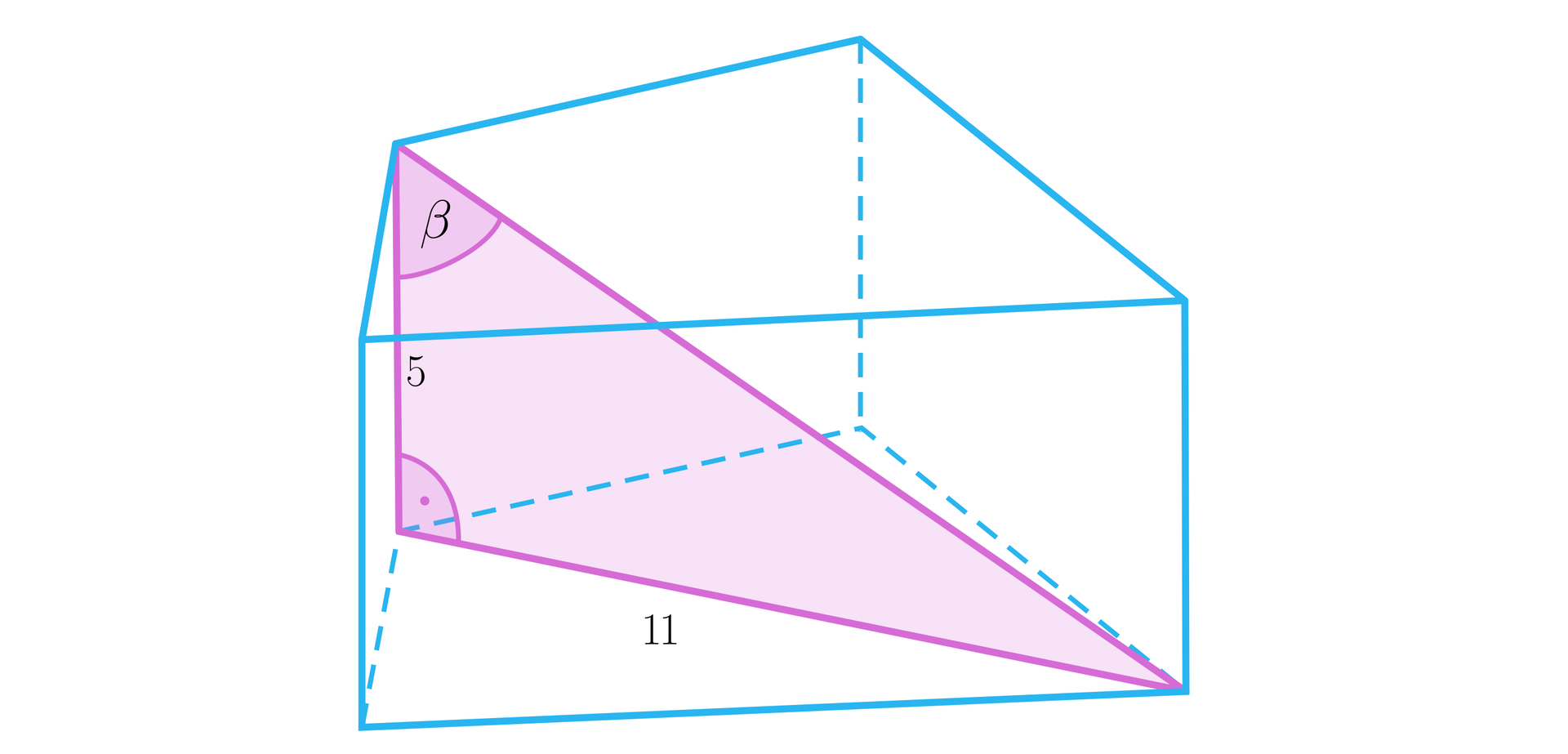
Sprawdź się
Graniastosłupy na rysunku są prostopadłościanami. Ustaw je w kolejności rosnącej miary kąta pomiędzy przekątną graniastosłupa, a krawędzią boczną (od lewej do prawej).
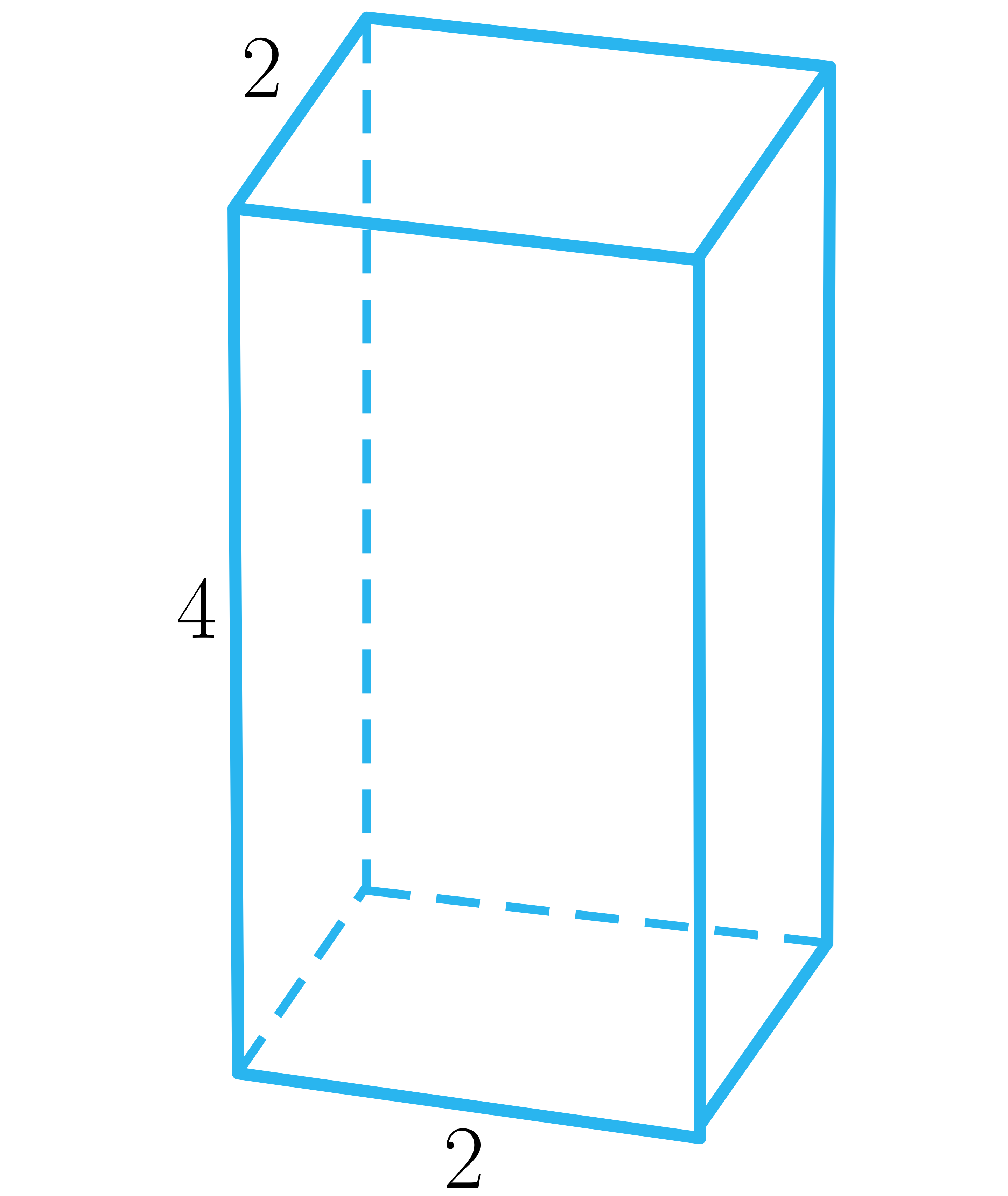
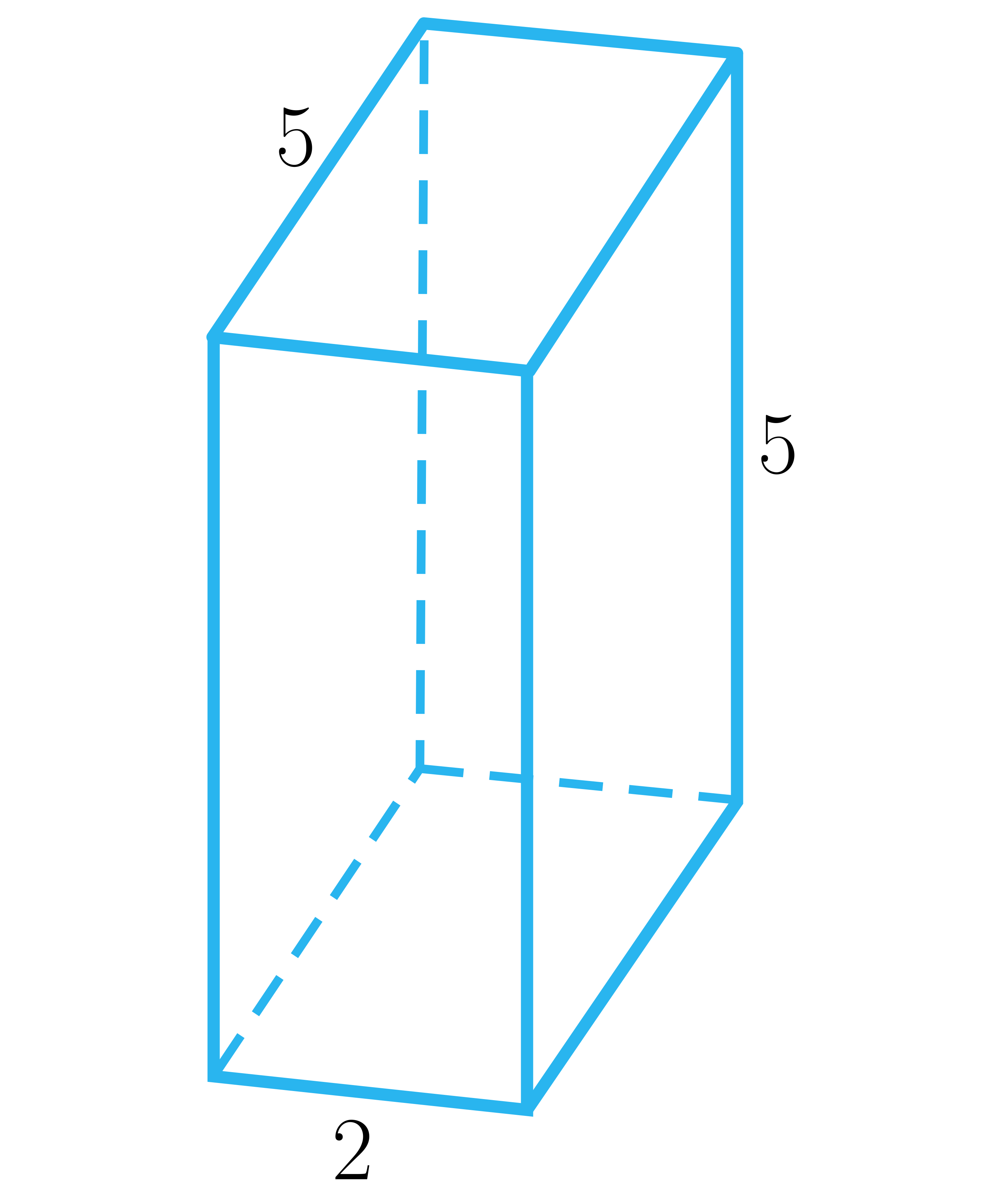
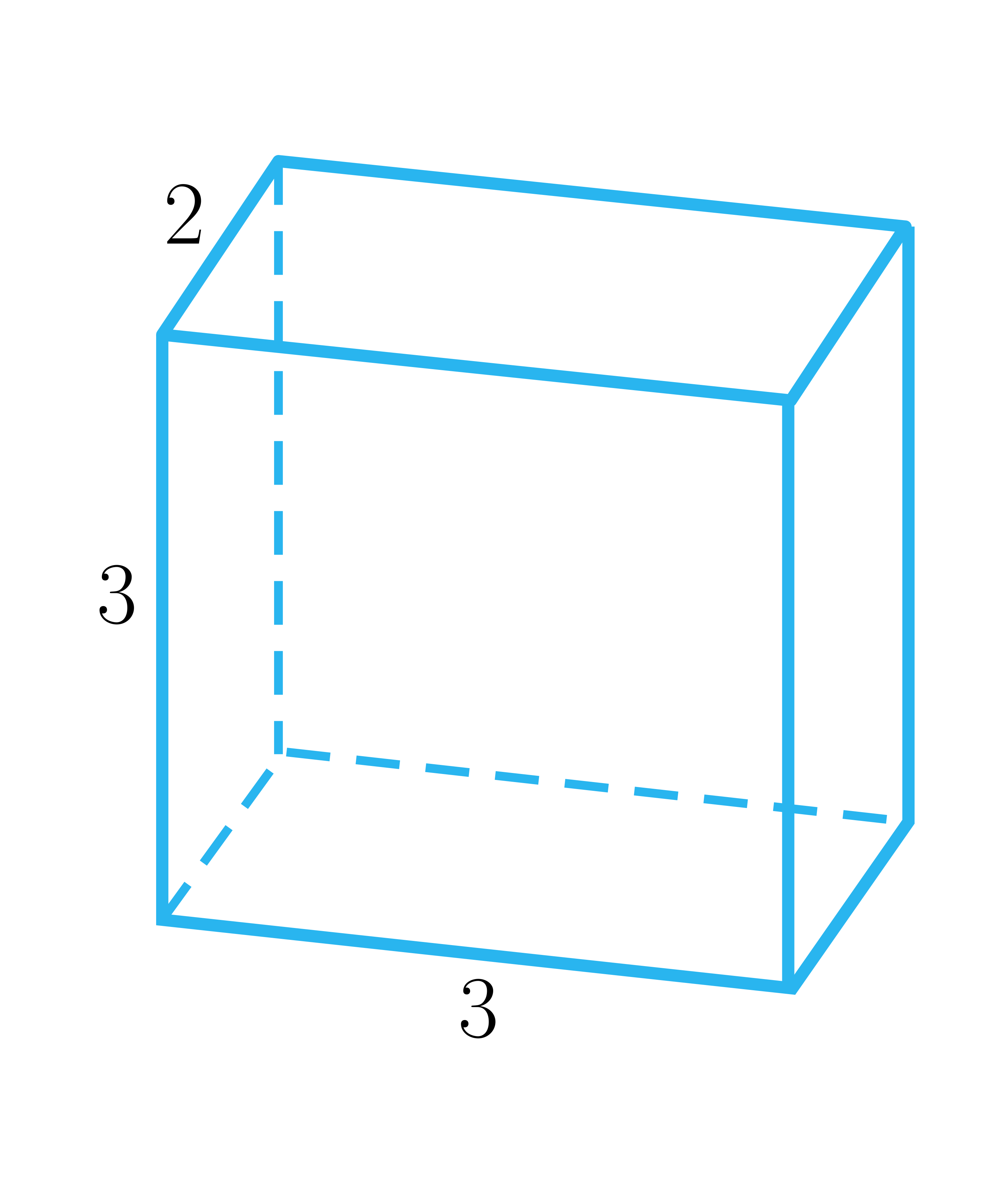
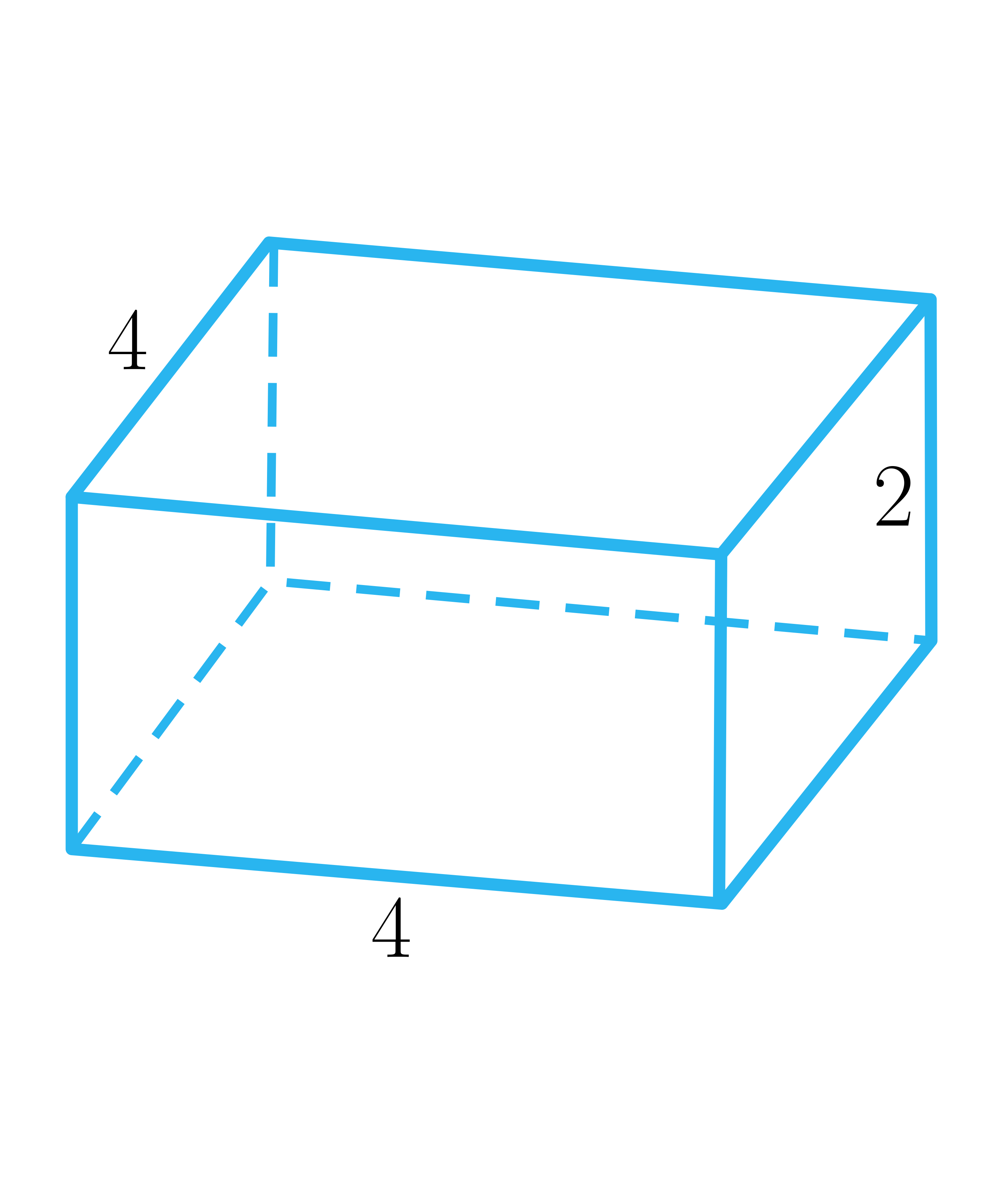
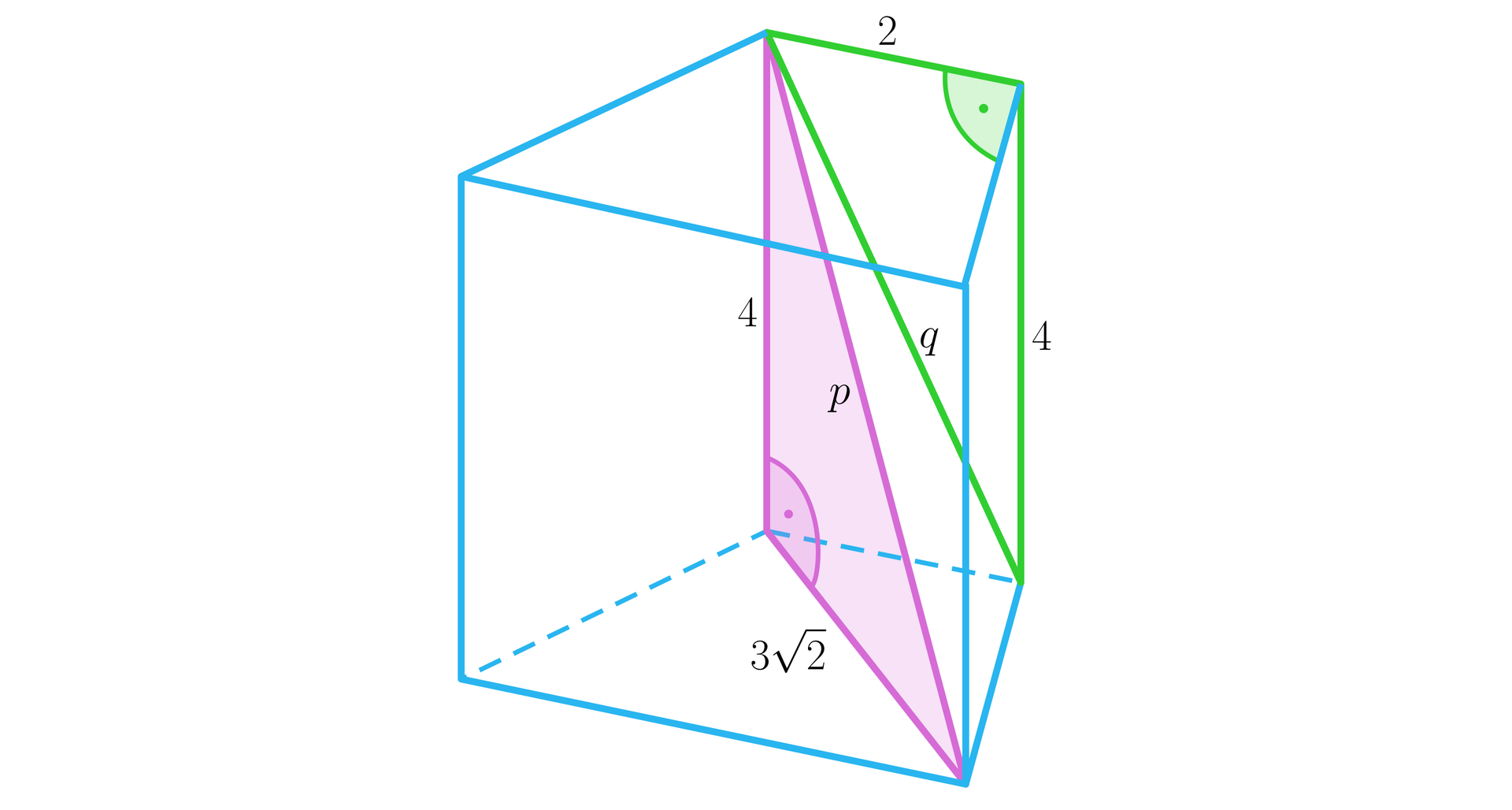
Oceń, czy poniższe zdania są prawdziwe czy fałszywe. Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Krawędź boczna ma długość ., 2. Wysokość ma długość ., 3. Sinus kąta pomiędzy krawędzią boczną a przekątną ściany bocznej wynosi ., 4. Kąt pomiędzy przekątną ściany bocznej a krawędzią boczną ma miarę większą od kąta pomiędzy przekątną ściany bocznej a krawędzią podstawy.
Zaznacz wszystkie poprawne odpowiedzi. Sinus kąta pomiędzy przekątną ściany bocznej graniastosłupa prawidłowego trójkątnego, a krawędzią podstawy wynosi , a krawędź podstawy ma długość . Wówczas:
- Krawędź boczna ma długość .
- Wysokość ma długość .
- Sinus kąta pomiędzy krawędzią boczną, a przekątną ściany bocznej wynosi .
- Kąt pomiędzy przekątną ściany bocznej, a krawędzią boczną ma miarę większą od kąta pomiędzy przekątną ściany bocznej, a krawędzią podstawy.
Podstawą graniastosłupa prostego jest romb o przekątnych długości i . Krawędź boczna tego graniastosłupa ma długość . Oceń prawdziwość zdań:
| Prawda | Fałsz | |
| Tangens kąta pomiędzy krótszą przekątną graniastosłupa, a krawędzią boczną wynosi . | □ | □ |
| Kąt pomiędzy przekątną ściany bocznej, a krawędzią boczną ma miarę ok. . | □ | □ |
| Cosinus kąta pomiędzy dłuższą przekątną graniastosłupa, krawędzią boczną jest większy od cosinusa kąta pomiędzy krótszą przekątną graniastosłupa a krawędzią boczną. | □ | □ |
| Ponieważ wszystkie przekątne ścian bocznych są tej samej długości, to kąty pomiędzy przekątnymi dowolnych sąsiadujących ze sobą ścian bocznych mają tę samą miarę. | □ | □ |
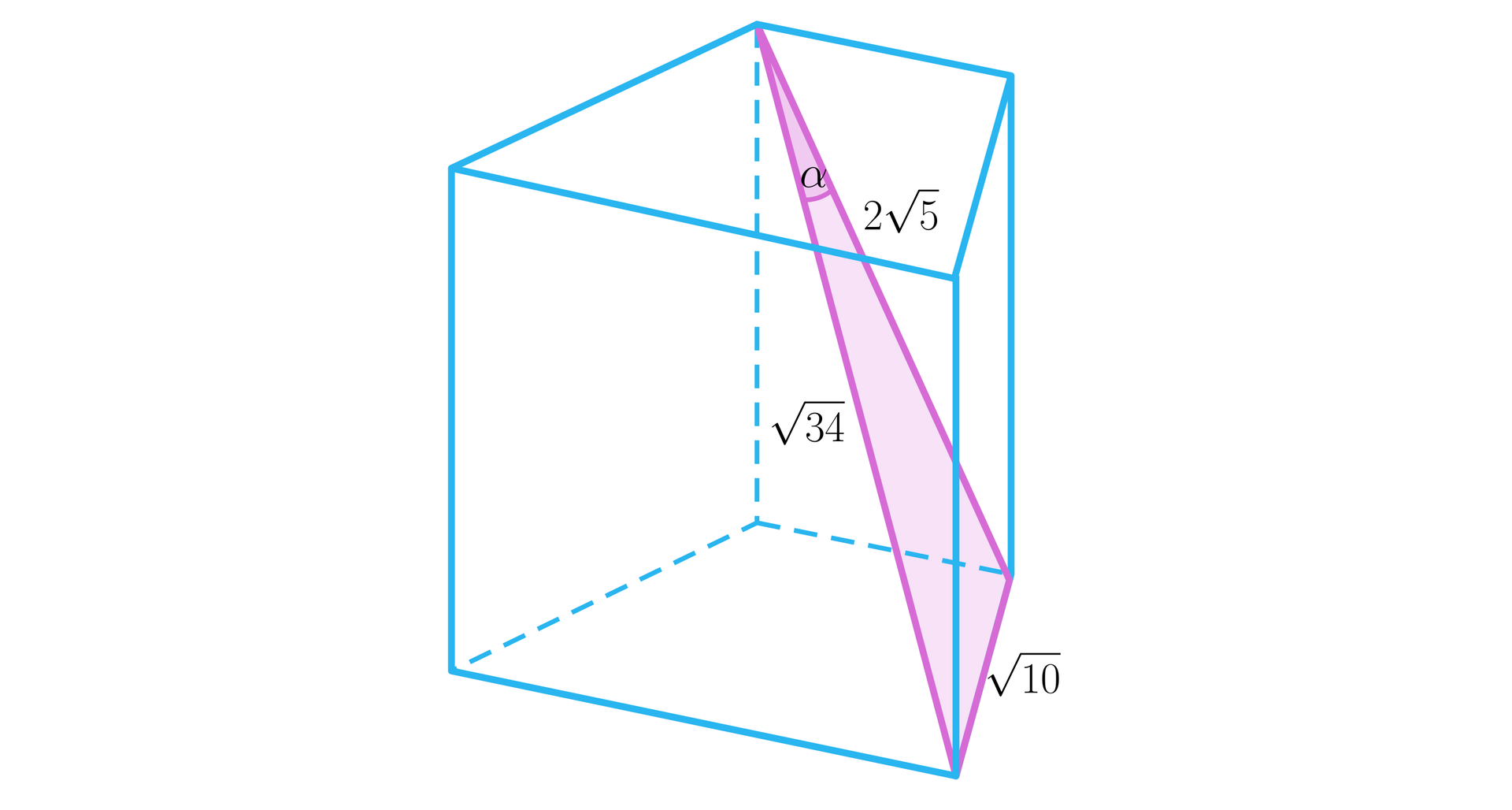
Zaznacz poprawną odpowiedź. Podstawą graniastosłupa prostego jest trójkąt prostokątny o przyprostokątnych i . Sinus kąta pomiędzy przekątną największej ściany bocznej, a krawędzią podstawy wynosi . Wówczas kąt pomiędzy przekątną najmniejszej ściany bocznej, a krawędzią boczną ma miarę:
Dany jest graniastosłup prawidłowy sześciokątny o krawędzi podstawy długości i wysokości . Dopasuj nazwy kątów w graniastosłupie do ich przybliżonej miary.
<span aria-label="siedemdziesiąt °" role="math"><math><mn>70</mn><mo>°</mo></math></span>, <span aria-label="dwadzieścia siedem °" role="math"><math><mn>27</mn><mo>°</mo></math></span>, <span aria-label="dwadzieścia cztery °" role="math"><math><mn>24</mn><mo>°</mo></math></span>, <span aria-label="siedemdziesiąt sześć °" role="math"><math><mn>76</mn><mo>°</mo></math></span>, <span aria-label="trzynaście °" role="math"><math><mn>13</mn><mo>°</mo></math></span>
| Kąt między krótszą przekątną graniastosłupa, a krawędzią podstawy. | |
| Kąt między krótszą i dłuższą przekątną graniastosłupa wychodzącymi z tego samego wierzchołka. | |
| Kąt między dłuższą przekątną graniastosłupa, a krawędzią boczną. | |
| Kąt między przekątnymi sąsiednich ścian bocznych. | |
| Kąt między przekątną ściany bocznej, a krawędzią podstawy. |
Wskaż najmniejszy przedział, do którego należy miara kąta między przekątną graniastosłupa czworokątnego a krawędzią jego podstawy:
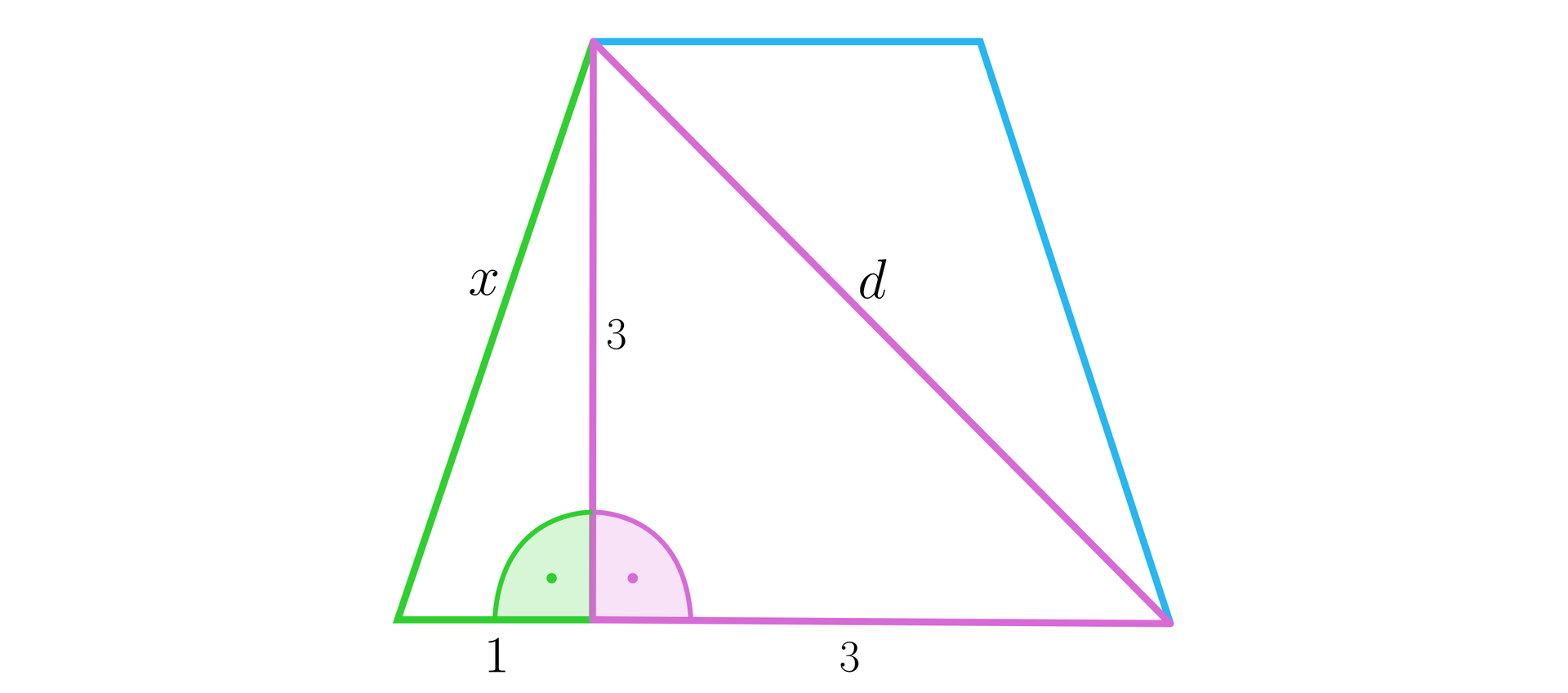
Podstawą graniastosłupa prostego jest trapez równoramienny o podstawach długości i oraz wysokości . Krawędź boczna tego graniastosłupa ma długość .
Oblicz miarę kąta pomiędzy przekątną graniastosłupa a przekątną najmniejszej ściany bocznej.
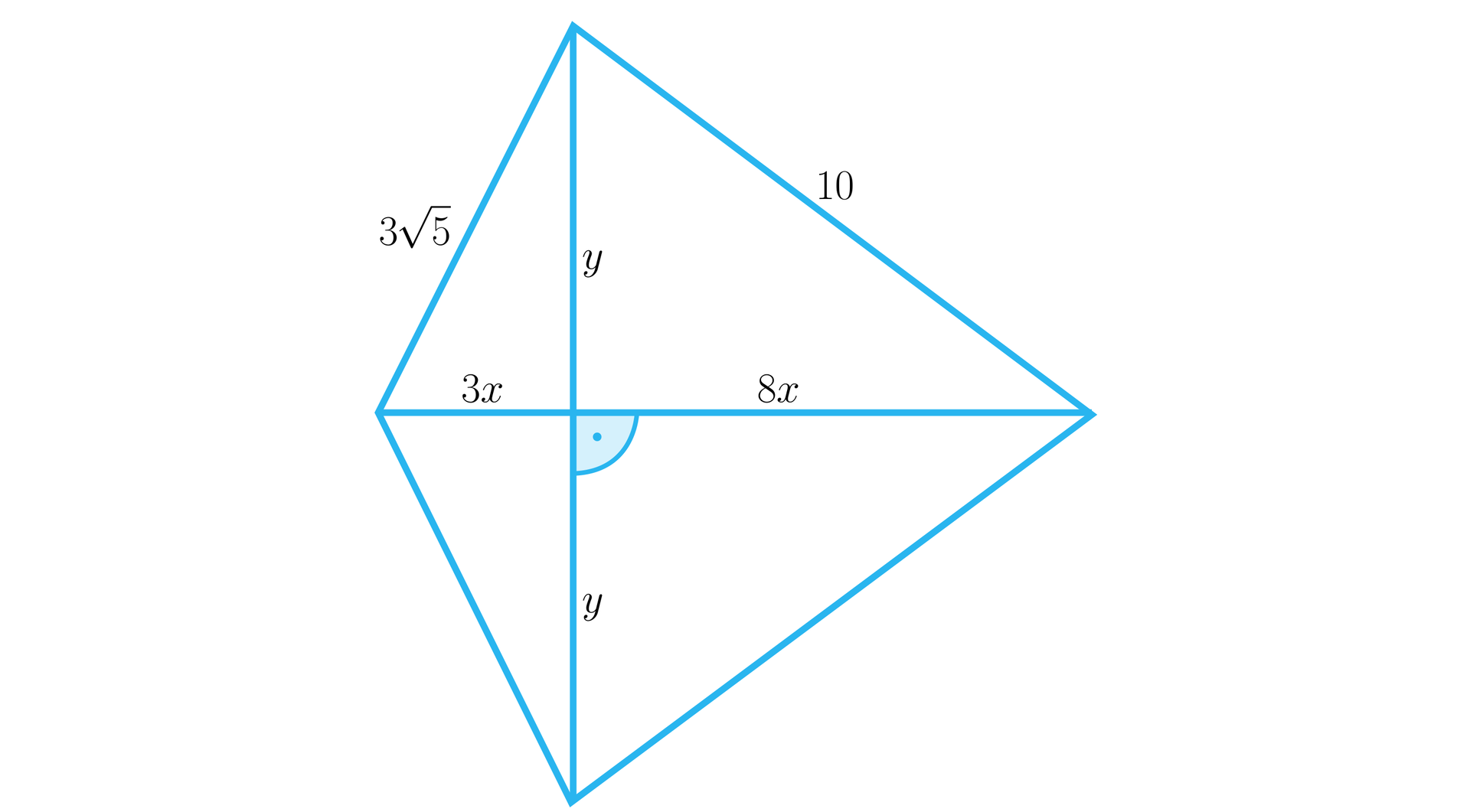
Podstawą graniastosłupa jest deltoid o bokach długości i . Punkt przecięcia przekątnych podstawy dzieli jedną z przekątnych w stosunku . Oblicz kąt pomiędzy krótszą przekątną graniastosłupa a krawędzią boczną, wiedząc, że cosinus kąta pomiędzy dłuższą przekątną a krawędzią boczną ma wartość .