Sprawdź się

Pokaż ćwiczenia:

R1RyAyPRBq87M1

Ćwiczenie 1

W ogrodzeniu prostokątnej działki zamontowano $2$ furtki o szerokości $1 m$ każda. Na ogrodzenie działki zużyto jeszcze $46 m$ bieżących siatki. Zaznacz największe możliwe pole powierzchni ogrodzonego obszaru.

$100 m^{2}$
$144 m^{2}$
$121 m^{2}$
$169 m^{2}$

RQeeH95yAWGks1

Ćwiczenie 2

Dany jest prostokąt o bokach

6 cm

21 cm

. Dobierz odpowiednią zmianę długości boków tego prostokąta do wartości

x

tak, aby pole otrzymanego prostokąta było największe. Krótszy bok tego prostokąta powiększamy o

x

, a dłuższy zmniejszamy o

3 x

Możliwe odpowiedzi: 1.

x = 4, 25

, 2.

x = 3, 75

, 3.

x = 1

, 4.

x = 0, 5

Krótszy bok tego prostokąta powiększamy o

2 x

, a dłuższy zmniejszamy o

2 x

Możliwe odpowiedzi: 1.

x = 4, 25

, 2.

x = 3, 75

, 3.

x = 1

, 4.

x = 0, 5

Krótszy bok tego prostokąta powiększamy o

\frac{1}{2} x

, a dłuższy zmniejszamy o

\frac{3}{2} x

Możliwe odpowiedzi: 1.

x = 4, 25

, 2.

x = 3, 75

, 3.

x = 1

, 4.

x = 0, 5

Krótszy bok tego prostokąta powiększamy o

3 x

, a dłuższy pomniejszamy o

2 x

Możliwe odpowiedzi: 1.

x = 4, 25

, 2.

x = 3, 75

, 3.

x = 1

, 4.

x = 0, 5

Dany jest prostokąt o bokach $6 cm$ i $21 cm$ . Dobierz odpowiednią zmianę długości boków tego prostokąta do wartości $x$ tak, aby pole otrzymanego prostokąta było największe.

Krótszy bok tego prostokąta powiększamy o $x$ , a dłuższy zmniejszamy o $3 x$ .
Krótszy bok tego prostokąta powiększamy o $2 x$ , a dłuższy zmniejszamy o $2 x$ .
Krótszy bok tego prostokąta powiększamy o $\frac{1}{2} x$ , a dłuższy zmniejszamy o $\frac{3}{2} x$ .
Krótszy bok tego prostokąta powiększamy o $3 x$ , a dłuższy pomniejszamy o $2x$ .

R1eN7k392S5ft1

Ćwiczenie 3

Dany jest prostokąt o obwodzie $60 cm$ . Wybierz zdania prawdziwe.

Prostokąt ten ma największe pole, jeśli jego wymiary to $10 cm$ i $20 cm$ .
Największe możliwe pole tego prostokąta wynosi $225 {cm}^{2}$ .
Najkrótsza możliwa przekątna tego prostokąta ma długość $\sqrt{450} cm$ .
Prostokąt ten ma najkrótszą możliwą przekątną, jeśli jego wymiary to $1 cm$ i $29 cm$ .

RwbSVQRum1LRo2

Ćwiczenie 4

Dany jest walec o obwodzie przekroju osiowego równym

60 cm

. W puste miejsca wstaw odpowiednie liczby całkowite. Walec, którego średnica podstawy wynosi 1.

16

, 2.

256

, 3.

169

, 4.

17

, 5.

17

, 6.

16

, 7.

225

, 8.

289

, 9.

13

, 10.

13

, 11.

15

, 12.

15

cm

, ma największe pole powierzchni bocznej.

Największe pole powierzchni bocznej ma walec o przekątnej przekroju osiowego równej 1.

16

, 2.

256

, 3.

169

, 4.

17

, 5.

17

, 6.

16

, 7.

225

, 8.

289

, 9.

13

, 10.

13

, 11.

15

, 12.

15

\sqrt{2} cm

.

Największe możliwe pole powierzchni bocznej tego walca wynosi 1.

16

, 2.

256

, 3.

169

, 4.

17

, 5.

17

, 6.

16

, 7.

225

, 8.

289

, 9.

13

, 10.

13

, 11.

15

, 12.

15

π {cm}^{2}

Dany jest walec o obwodzie przekroju osiowego równym $60 cm$ . W puste miejsca wstaw odpowiednie liczby całkowite.

$256$ , $16$ , $15$ , $17$ , $225$ , $13$ , $16$ , $15$ , $13$ , $289$ , $169$ , $17$

Walec, którego średnica podstawy wynosi ............ $cm$ , ma największe pole powierzchni bocznej.

Największe pole powierzchni bocznej ma walec o przekątnej przekroju osiowego równej ............ $\sqrt{2} cm$ .

Największe możliwe pole powierzchni bocznej tego walca wynosi ............ $π {cm}^{2}$ .

RZZ6zOdeIZlH72

Ćwiczenie 5

Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego wynosi $72 cm$ . W którym przypadku graniastosłup osiąga największe pole powierzchni bocznej?

Krawędź podstawy ma długość $6 cm$ a wysokość ma długość $3 cm$ .
Krawędź podstawy ma długość $6 cm$ i wysokość ma długość $6 cm$ .
Krawędź podstawy ma długość $3 cm$ a wysokość ma długość $6 cm$ .
Krawędź podstawy ma długość $3 cm$ i wysokość ma długość $3 cm$ .

R10owj18ndTmy2

Ćwiczenie 6

Łączenie par. Suma długości wysokości i obu podstaw trapezu równoramiennego wynosi

14 cm

. Oceń prawdziwość poniższych zdań. Przy każdym zdaniu w tabeli zaznacz „Prawda” albo „Fałsz”. . Trapez ten osiąga największe pole przy wysokości równej

7 cm

.. Możliwe odpowiedzi: Prawda, Fałsz. Największe możliwe pole tego trapezu wynosi

24, 5 {cm}^{2}

.. Możliwe odpowiedzi: Prawda, Fałsz. Długość przekątnej takiego trapezu o największym polu wynosi

7 \sqrt{2} cm

.. Możliwe odpowiedzi: Prawda, Fałsz

Suma długości wysokości i obu podstaw trapezu równoramiennego wynosi $14 cm$ . Oceń prawdziwość poniższych zdań.

Zdanie	Prawda	Fałsz
Trapez ten osiąga największe pole przy wysokości równej $7 cm$ .	□	□
Największe możliwe pole tego trapezu wynosi $24, 5 {cm}^{2}$ .	□	□
Długość przekątnej takiego trapezu o największym polu wynosi $7 \sqrt{2} cm$ .	□	□

RJXQ6HfNhBTUH3

Ćwiczenie 7

Odcinek o długości $32 cm$ dzielimy na dwie części. Z jednej tworzymy kwadrat, natomiast z drugiej prostokąt, w którym stosunek długości boków wynosi $7 : 1$ . Odcinek dzielimy tak, aby suma pól kwadratu i prostokąta była najmniejsza. Wybierz zdania prawdziwe.

Bok kwadratu musi mieć długość $\frac{56}{23}$ .
Dłuższy bok prostokąta musi mieć długość $\frac{32}{23}$ .
Obwód prostokąta powinien wynosić $\frac{512}{23}$ .
Odcinek musimy podzielić na dwie równe części, każda o długości $16$ .

Ćwiczenie 8

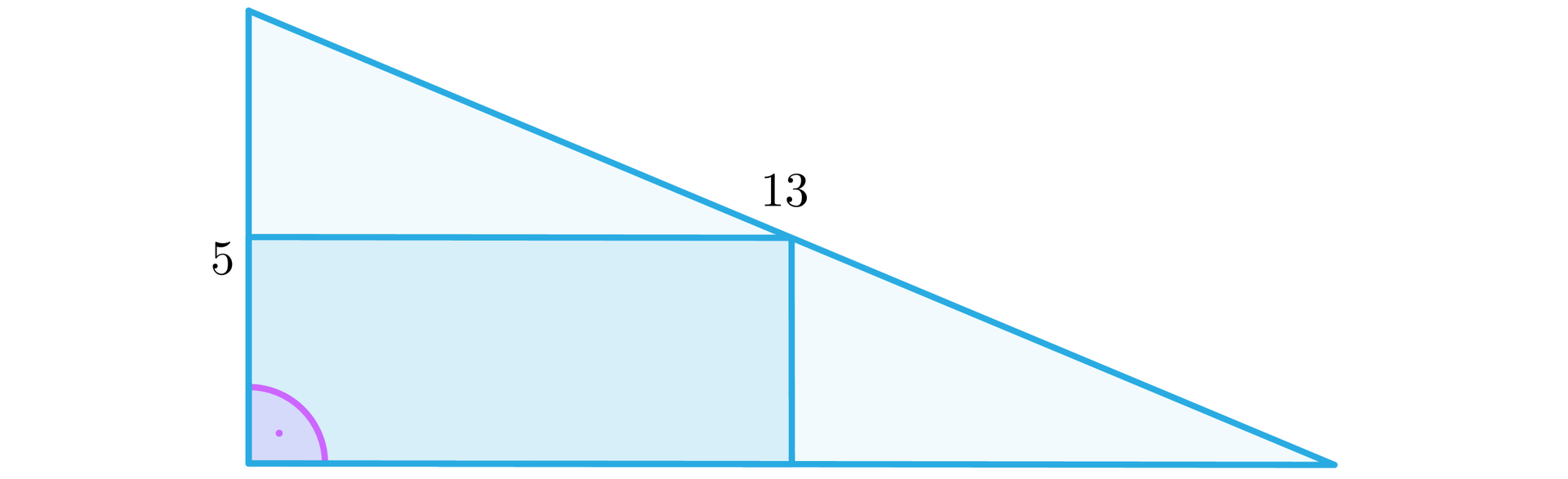
W trójkąt prostokątny o jednej z przyprostokątnych długości $5$ i przeciwprostokątnej długości $13$ wpisano prostokąt jak na rysunku poniżej.

R185AmIcdhJas

Ilustracja przedstawia trójkąt prostokątny, jego przeciwprostokątna ma długość trzynaście, jego krótsza pionowa przyprostokątna ma długość pięć. W trójkąt wpisano prostokąt, jego dwa boki leżą na przyprostokątnych, a jeden z wierzchołków leży na przeciwprostokątnej.

Rc9H4klp08izt

Animacja

Dla nauczyciela