Sprawdź się
Dany jest wykres funkcji .
Zaznacz wartość ilorazu różnicowego w punkcie , gdy oraz :
Na rysunku przedstawiono wykres pewnej funkcji oraz zaznaczono punkty i , które należą do tego wykresu.
Zaznacz zdania, które są prawdziwe.
- Jeżeli przyrost , to iloraz różnicowy funkcji w punkcie wynosi .
- Tangens kąta nachylenia siecznej do osi odciętych jest równy .
- Dla punktów i zachodzi równość: .
- Tangens kąta nachylenia siecznej do osi odciętych jest równy .
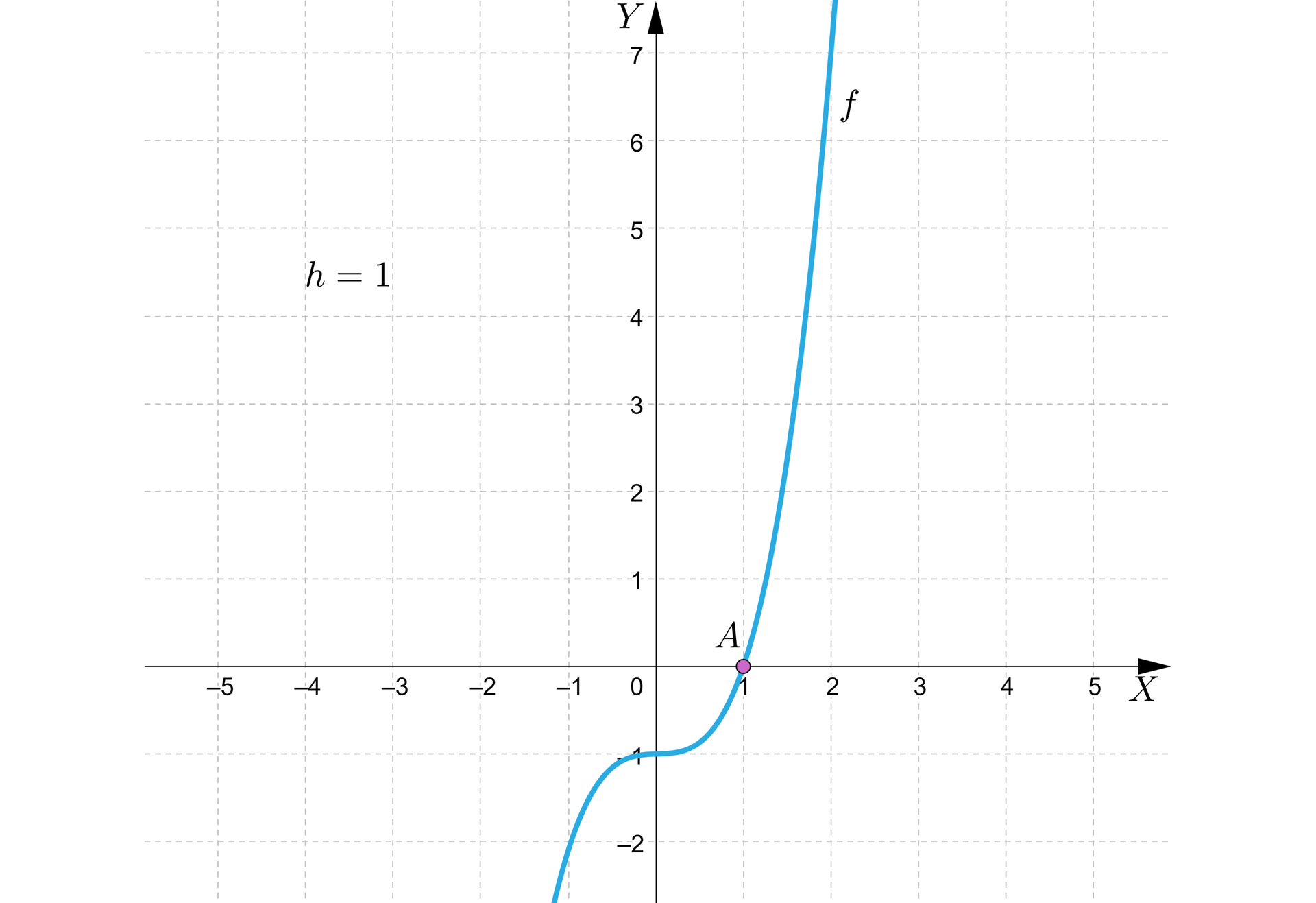
Dany jest wykres funkcji .
{}
{}
{}
{}
Zatem:
{}
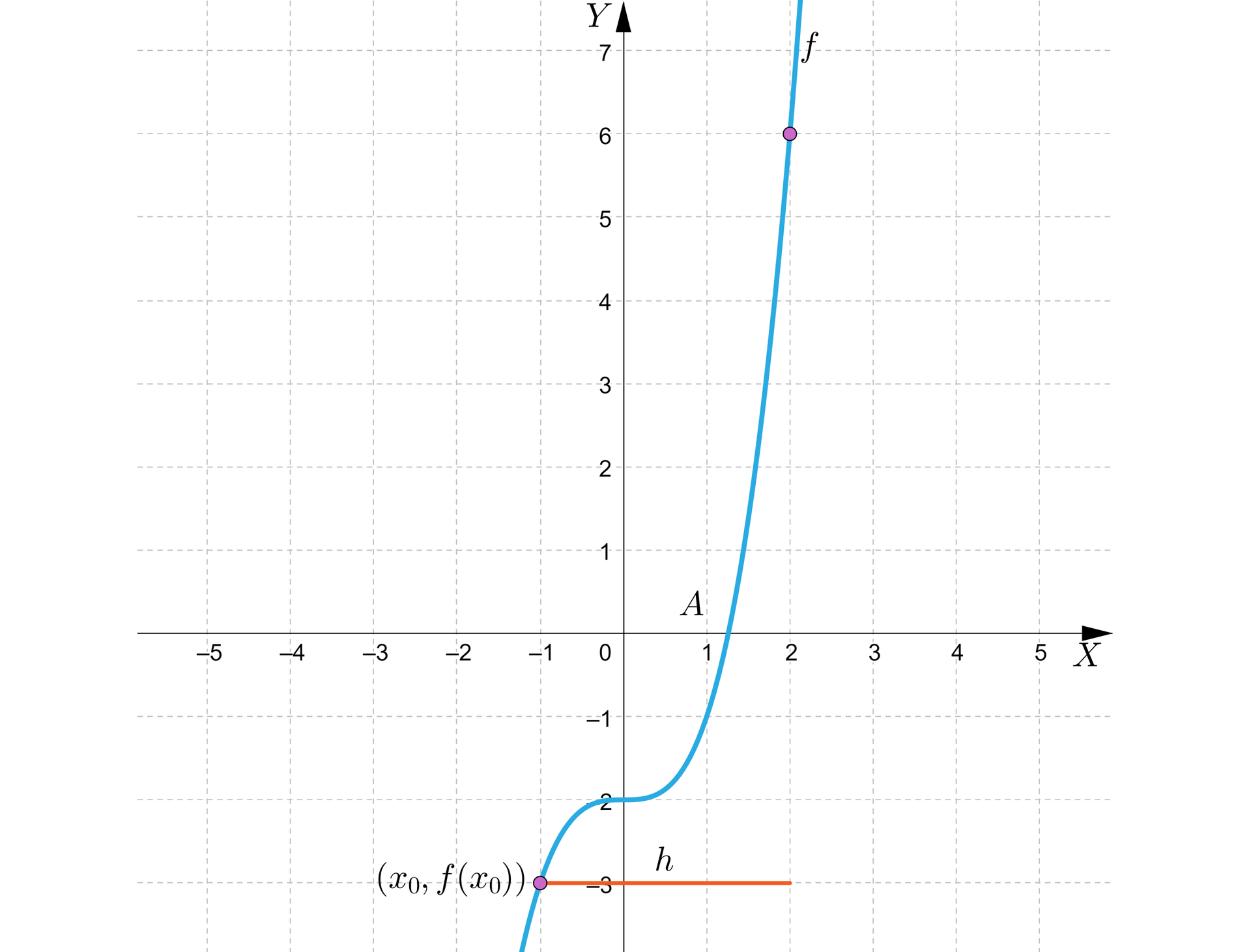
Na podstawie rysunku wstaw w tekst odpowiednie liczby.
, , , ,
Z wykresu funkcji odczytujemy:
............,
............,
............,
.............
Zatem:
.............
- zaznaczony punkt należący do wykresu ma współrzędne ,
- ,
- ,
- punkt o współrzędnych to punkt 1. , 2. , 3. 1. , 2. , 3. ,
- iloraz różnicowy wynosi 1. , 2. , 3. .
Na podstawie rysunku uzupełnij tekst odpowiednimi liczbami.
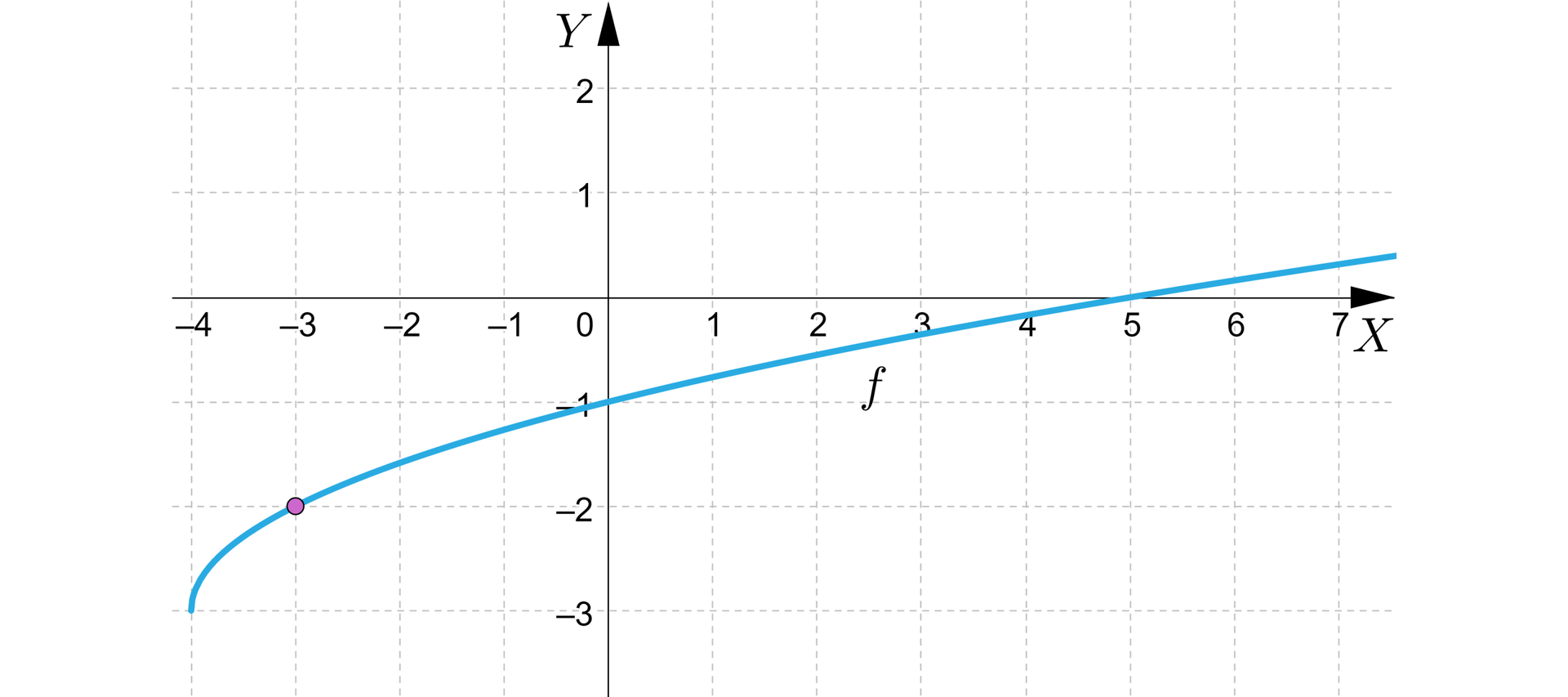
Jeżeli , to ............. Gdy przyrost argumentu , to ............ oraz .............
Wtedy iloraz różnicowy funkcji wynosi .
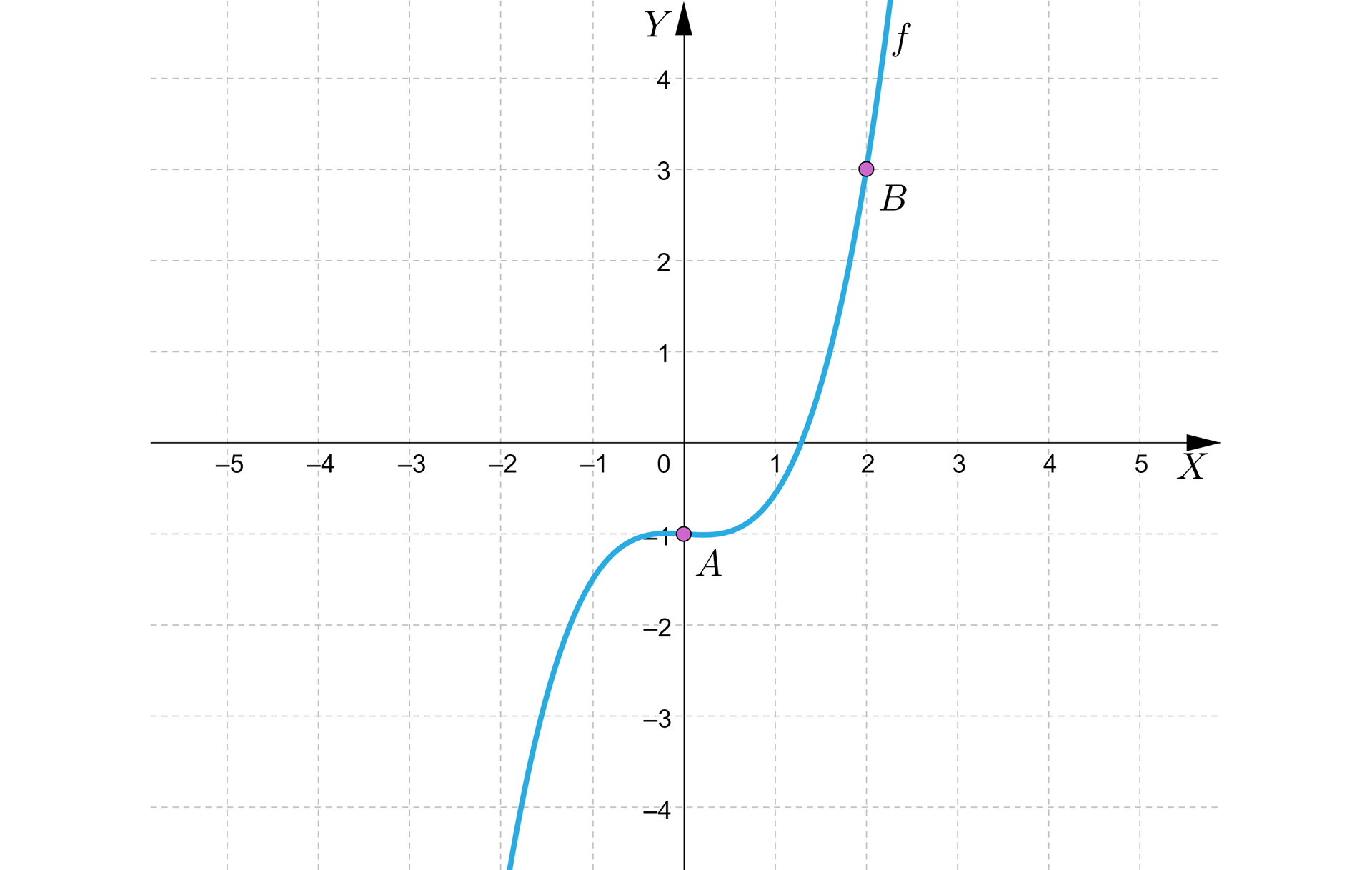
Jeżeli , to ............. Gdy przyrost argumentu , to ............ oraz .............
Wtedy iloraz różnicowy funkcji wynosi .
- zaznaczony punkt należący do wykresu ma współrzędne ,
- Tu uzupełnij,
- ,
- punkt o współrzędnych to punkt Tu uzupełnijTu uzupełnij,
- iloraz różnicowy wynosi Tu uzupełnij.
- Funkcja określona jest wzorem:
- zaznaczony punkt należący do wykresu ma współrzędne ,
- ,
- ,
- iloraz różnicowy wynosi 1. , 2. , 3. .
- Funkcja określona jest wzorem:
- zaznaczony punkt należący do wykresu ma współrzędne ,
- ,
- ,
- iloraz różnicowy wynosi 1. , 2. , 3. .
- Funkcja określona jest wzorem:
- zaznaczony punkt należący do wykresu ma współrzędne ,
- ,
- ,
- iloraz różnicowy wynosi 1. , 2. , 3. .
Na rysunku przedstawiono wykresy funkcji i .
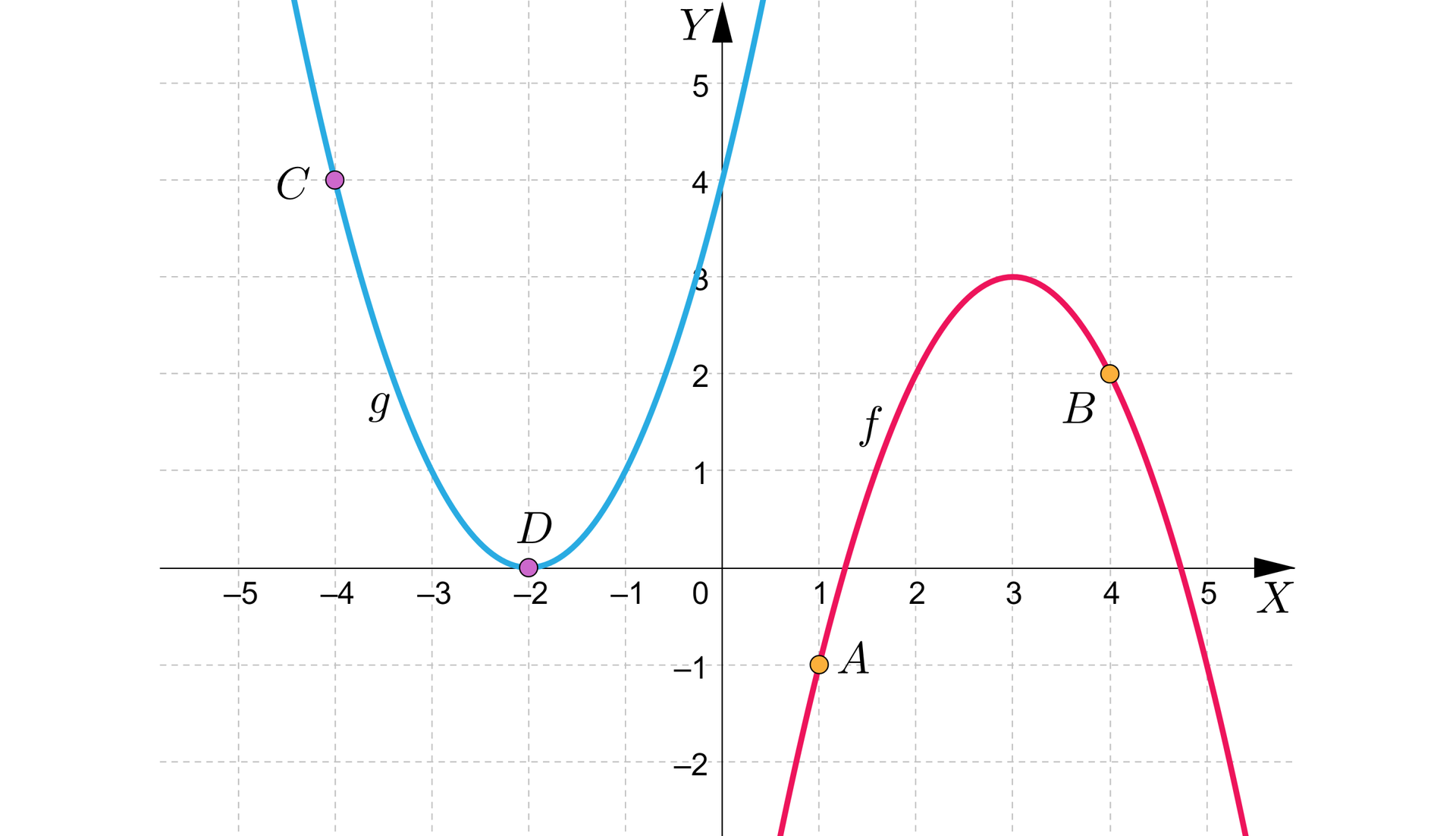
Dane są dwie funkcje. Pierwsza z nich określona jest wzorem oraz funkcja . Na wykresie funckji wyróżniono dwa punkty: oraz . Na wykresie funckji wyróżniono dwa punkty: oraz . Na podstawie tych informacji, wykonaj poniższe zadanie.
Pogrupuj elementy, zgodnie z podanym opisem.
jeżeli <span aria-label="x indeks dolny, zero, równa się, jeden" role="math"><math><msub><mi>x</mi><mn>0</mn></msub><mo>=</mo><mn>1</mn></math></span> oraz <span aria-label="h, równa się, trzy" role="math"><math><mi>h</mi><mo>=</mo><mn>3</mn></math></span>, to iloraz różnicowy funkcji wynosi <span aria-label="jeden" role="math"><math><mn>1</mn></math></span>, wartość współczynnika <span aria-label="b" role="math"><math><mi>b</mi></math></span> równania siecznej poprowadzonej przez zaznaczone punkty wynosi <span aria-label="nawias, minus, dwa, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mo>-</mo><mn>2</mn></mrow></mfenced></math></span>, kąt nachylenia do osi <span aria-label="X" role="math"><math><mi>X</mi></math></span> siecznej przechodzącej przez zaznaczone punkty ma miarę około <span aria-label="sześćdziesiąt cztery °" role="math"><math><mn>64</mn><mo>°</mo></math></span>, wartość współczynnika <span aria-label="b" role="math"><math><mi>b</mi></math></span> równania siecznej poprowadzonej przez zaznaczone punkty wynosi <span aria-label="nawias, minus, cztery, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mo>-</mo><mn>4</mn></mrow></mfenced></math></span>, jeżeli <span aria-label="x indeks dolny, zero, równa się, minus, cztery" role="math"><math><msub><mi>x</mi><mn>0</mn></msub><mo>=</mo><mo>-</mo><mn>4</mn></math></span> i <span aria-label="h, równa się, dwa" role="math"><math><mi>h</mi><mo>=</mo><mn>2</mn></math></span>, to iloraz różnicowy funkcji wynosi <span aria-label="nawias, minus, dwa, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mo>-</mo><mn>2</mn></mrow></mfenced></math></span>, kąt nachylenia do osi <span aria-label="X" role="math"><math><mi>X</mi></math></span> siecznej przechodzącej przez zaznaczone punkty ma miarę <span aria-label="czterdzieści pięć °" role="math"><math><mn>45</mn><mo>°</mo></math></span>
| Dla wykresu funkcji mamy: | |
|---|---|
| Dla wykresu funkcji mamy: |
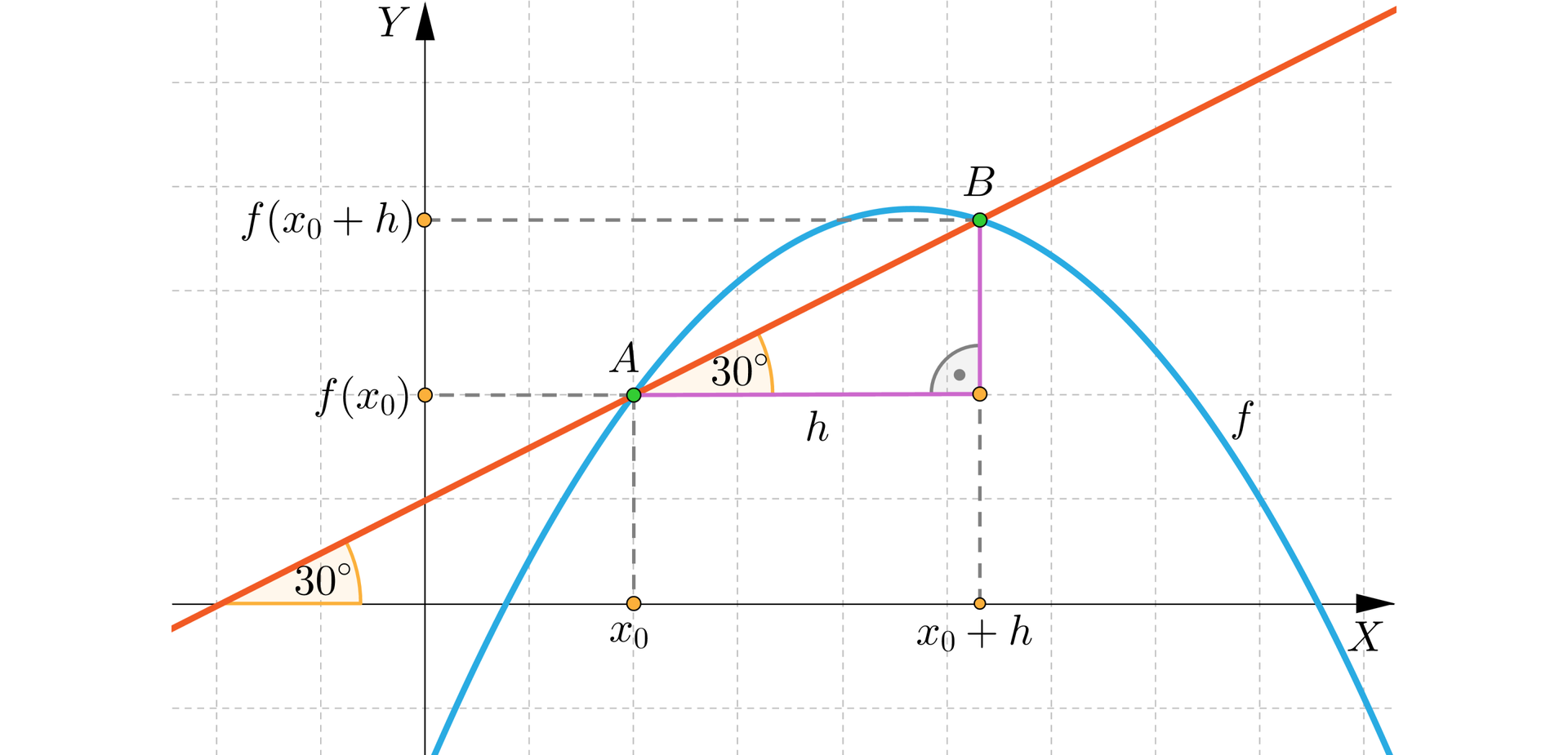
Prosta o równaniu jest sieczną do wykresu funkcji określonej wzorem . Wyznacz wartość przyrostu , dla którego dana prosta jest sieczną do wykres funkcji .
Wykaż, że jeśli zachodzi równość , to sieczna do wykresu funkcji poprowadzona w punkcie i zadanym przyroście , gdy jest nachylona do osi pod kątem .