Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Rozważmy graniastosłup prawidłowy sześciokątny, którego długości krawędzi wychodzących z jednego wierzchołka wynoszą $3 \sqrt{6}$ , $3 \sqrt{6}$ , oraz $4 \sqrt{5}$ .

RUu7KvW2zANBL

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, i wysokości bryły równej h. Zaznaczono dłuższą przekątną D1 bryły, oraz krótszą przekątną D2. Zaznaczono trójkąt o bokach a, D2, oraz D1.

Rau19PjDzGw1e

Ćwiczenie 2

Mając dane długości przekątnych w graniastosłupie prawidłowym sześciokątnym dopasuj do nich jego wymiary. Przeciągnij odpowiednie wartości.

Mając dane długości przekątnych w graniastosłupie prawidłowym sześciokątnym dopasuj do nich jego wymiary. Wybierz z listy rozwijalnej odpowiednie wartości.

RlJ8Vdi80m7oV

R1LTKwCqKRtW6

Ćwiczenie 3

W graniastosłupie prawidłowym sześciokątnym o polu podstawy $300 \sqrt{3} {cm}^{2}$ przekątne ścian bocznych wychodzące z jednego wierzchołka wraz z przekątną przeciwległej podstawy tworzą trójkąt. Wyznacz jego pole i kąty w tym trójkącie, jeżeli krawędź boczna graniastosłupa jest cztery razy dłuższa od krawędzi podstawy.

R1QcR592e46pM

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy o długości a i o wysokości h. Obrano pewien górny wierzchołek, z którego poprowadzono przekątne dwóch sąsiadujących ze sobą ścian o długości d każda. Dolne końce tych przekątnych połączono odcinkiem biegnącym po dolnej podstawie. Odcinek ten oznaczono jako d o indeksie dolnym dwa. Odcinek ten jest krótszą przekątną podstawy graniastosłupa.

Graniastosłup jest prawidłowy sześciokątny, zatem jego podstawą jest sześciokąt foremny o znanym polu $300 \sqrt{3} {cm}^{2}$ .

Obliczamy długość $a$ krawędzi podstawy – korzystamy ze wzoru na pole sześciokąta foremnego:
$P = \frac{3 a^{2} \sqrt{3}}{2}$ ,
$300 \sqrt{3} = \frac{3 a^{2} \sqrt{3}}{2}$ .

Krawędź podstawy wynosi: $a = 10 \sqrt{2}$ .

Wszystkie krawędzie boczne graniastosłupa są równe i mają długość cztery razy dłuższa od krawędzi podstawy czyli $h = 40 \sqrt{2}$ .

Stąd długość $d = 10 \sqrt{3} 4$ , $d_{2} = 10 \sqrt{6}$ .

Otrzymaliśmy trójkąt równoramienny, w którym:
$x = 5 \sqrt{130} > P_{△} = 50 \sqrt{195}$ .

R35mStyYmV0E3

Ilustracja przedstawia trójkąt równoramienny o ramionach o długości d każde i o wysokości między nimi oznaczonej jako x. Wysokość dzieli dolną podstawę na pół, czyli na dwa odcinki o długości jedna druga razy d indeks dolny dwa.

Z twierdzenia cosinusów obliczymy kąt $α$ między ramionami trójkąta: $\cos α = \frac{31}{34}$ , czyli $α \approx 24$ $°$ .

Kąty w omawianym trójkącie wynoszą w zaokrągleniu odpowiednio: $24 °$ , $78 °$ i $78 °$ .

Ćwiczenie 4

Podstawą graniastosłupa prawidłowego jest sześciokąt o krótszej przekątnej długości $6 \sqrt{15} cm$ . Wysokość graniastosłupa jest $2 \sqrt{5}$ razy większa od jego krawędzi podstawy.

RTLU6LmsAmUuV

R1SF3XZgb5mye

Wyznacz przekątne tego graniastosłupa i uzupełnij luki odpowiednimi z podanych wartości. Graniastosłup jest prawidłowy sześciokątny, zatem jego podstawą jest sześciokąt foremny o znanej krótszej przekątnej

d_{2} = 6 \sqrt{15}

cm

.
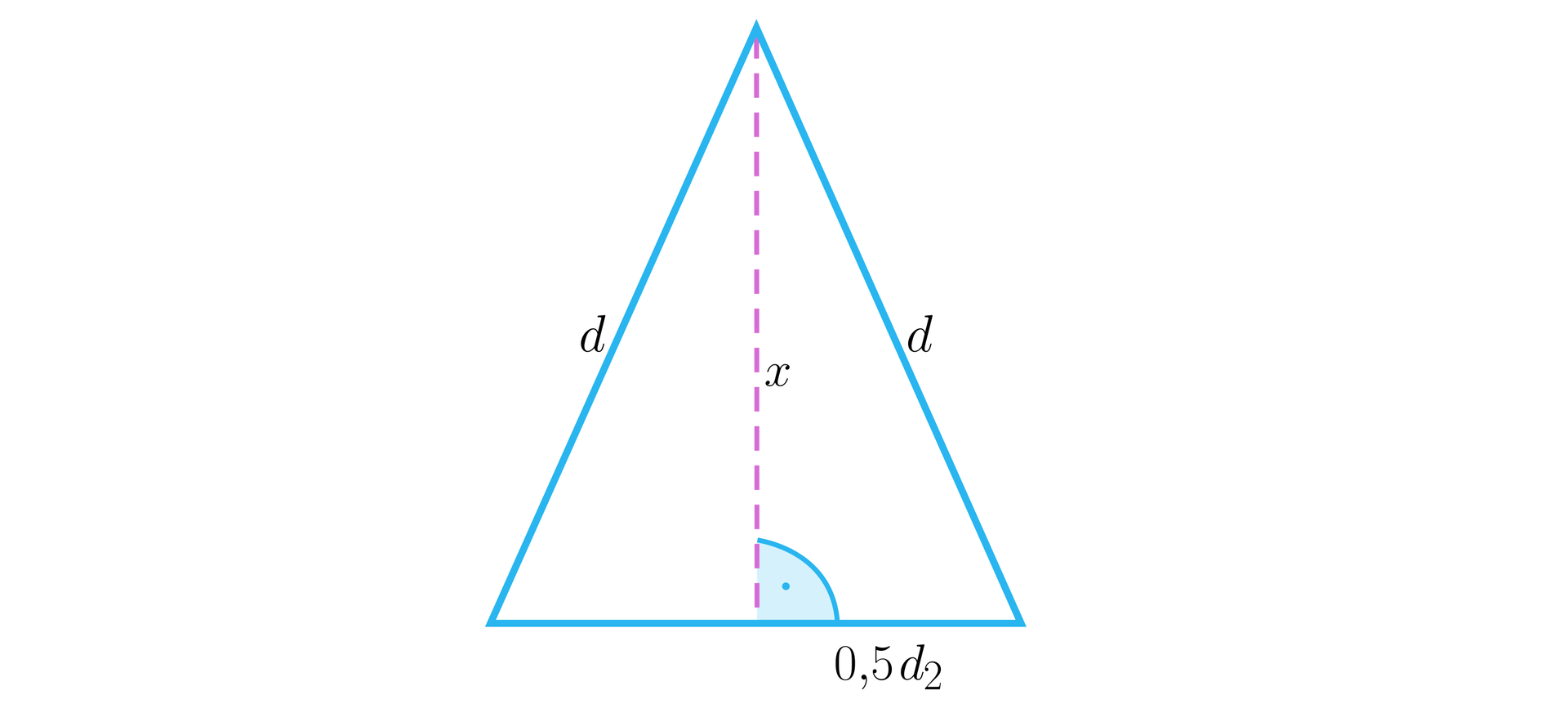
Obliczamy długość

a

krawędzi podstawy – korzystamy ze wzoru

d_{2} = a \sqrt{3}

a =

2 \sqrt{5}

, 2.

6 \sqrt{115}

, 3.

6 \sqrt{5}

, 4.

60

, 5.

12 \sqrt{30}

cm

.
Wszystkie krawędzie boczne graniastosłupa są równe i mają długość 1.

2 \sqrt{5}

, 2.

6 \sqrt{115}

, 3.

6 \sqrt{5}

, 4.

60

, 5.

12 \sqrt{30}

razy większą od jego krawędzi podstawy, czyli

h =

2 \sqrt{5}

, 2.

6 \sqrt{115}

, 3.

6 \sqrt{5}

, 4.

60

, 5.

12 \sqrt{30}

cm

.
Natomiast

D_{1} =

2 \sqrt{5}

, 2.

6 \sqrt{115}

, 3.

6 \sqrt{5}

, 4.

60

, 5.

12 \sqrt{30}

cm

D_{2} =

2 \sqrt{5}

, 2.

6 \sqrt{115}

, 3.

6 \sqrt{5}

, 4.

60

, 5.

12 \sqrt{30}

cm

Ćwiczenie 5

Graniastosłup prawidłowy sześciokątny ma równe wszystkie krawędzie. Suma ich długości wynosi $S cm$ . Wyznacz sumę długości wszystkich krótszych przekątnych tego graniastosłupa.

Rr8xpTQUdLKYi

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny, na którym zaznaczono wszystkie krótsze przekątne bryły. Z każdego wierzchołka dolnej podstawy wychodzą po dwie przekątne.

Omawiany graniastosłup ma $S_{k} = S (cm)$ oraz wszystkie równe krawędzie czyli rozpisując otrzymujemy:
$S_{k} = 18 \cdot a = S$ ,
$a = h = \frac{S}{18}$ $(cm)$ .

W naszym graniastosłupie mamy $12$ krótszych przekątnych, (na rysunku widzimy, że z każdego wierzchołka dolnej podstawy wychodzą po dwie przekątne).

Suma tych przekątnych wynosi:
$12 \cdot D_{2} = 12 \cdot 2 a = 24 \cdot \frac{S}{18} = \frac{4}{3} S (cm)$ .

Suma przekątnych wynosi $\frac{4}{3} S cm$ .

Ćwiczenie 6

Zbadaj, czy wysokość, krótsza i dłuższa przekątna graniastosłupa prawidłowego sześciokątnego w podanej kolejności tworzą ciąg geometryczny?

Rlz69hLj1dC9i

Mamy $a > 0$ , $h > 0$ . Załóżmy, że podane wielkości tworzą ciąg geometryczny.

Zapisujemy, że $h$ , $D_{2}$ , $D_{1}$ - to ciąg geometryczny, więc spełniają warunek: ${D_{2}}^{2} = h \cdot D_{1}$ .
Otrzymujemy równanie: $3 a^{2} + h^{2} = h \sqrt{4 a^{2} + h^{2}}$ .
A następnie, po przekształceniu:
$9 a^{4} + 6 a^{2} h^{2} + h^{4} = h^{2} (4 a^{2} + h^{2})$ ,
$9 a^{4} + 2 a^{2} h^{2} = 0$ ,
$a^{2} \cdot (9 a^{2} + 2 h^{2}) = 0$ ,
$a^{2} = 0$ lub $9 a^{2} + 2 h^{2} = 0$ ,
$a = 0$ lub $a = 0$ i $h = 0$ .

Otrzymujemy ostatecznie, że $a = 0$ i $h = 0$ , co jest sprzeczne z założeniem początkowym $a > 0$ , $h > 0$ , ponieważ są długościami krawędzi.

Ćwiczenie 7

Różnica długości przekątnych graniastosłupa prawidłowego sześciokątnego wynosi $10 cm$ , a jego wysokość $20 cm$ . Wyznacz długość krawędzi podstawy tej bryły.

R1AuE7oquZ03p

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, i wysokości h równej dwadzieścia. Zaznaczono dłuższą przekątną D1 bryły, oraz krótszą przekątną D2.

Rozpisując warunki zadania, otrzymujemy:
$D_{1} - D_{2} = 10$
$\sqrt{4 a^{2} + 400} - \sqrt{3 a^{2} + 400} = 10$
$a^{4} - 1400 a^{2} - 150000 = 0$

Rozwiązując równanie dwukwadratowe, otrzymujemy $a$ .

Długość podstawy wynosi $a = 10 \sqrt{15} cm$ .

Ćwiczenie 8

Dany jest graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej $6 cm$ . Graniastosłup przecięto płaszczyzną jak na rysunku. Otrzymano w ten sposób przekrój o polu równym $72 \sqrt{2}$ . Wyznacz przekątne tego graniastosłupa.

R1cjUxR8MhK4a

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o podstawie dolnej ABCDEF, oraz górnej GHIJKL. Punkt O, stanowi środek krawędzi bocznej AG. Punkt P, stanowi środek krawędzi bocznej DJ. Krawędź podstawy jest równa sześć, natomiast wysokość bryły jest równa 2x. Graniastosłup przecięto w taki sposób, że uzyskano płaszczyznę przecięcia w postaci wielokąta o wierzchołkach BCPKLO.

Zaznaczony przekrój dzielimy na dwa trapezy równoramienne.
Wysokość trapezu: $h = 4 \sqrt{2} cm$ .
$D_{2} = 2 h$ , a $D_{1}$ obliczamy z twierdzenia Pitagorasa.

Długości przekątnych wynoszą $D_{1} = 2 \sqrt{41} cm$ i $D_{2} = 8 \sqrt{2} cm$ .

Animacja 3D

Dla nauczyciela