Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na rysunkach przedstawiono fragmenty pochodnych pewnych funkcji różniczkowalnych. Na tej podstawie oceń prawdziwość każdego zdania.

R1dQUV9gHtYav

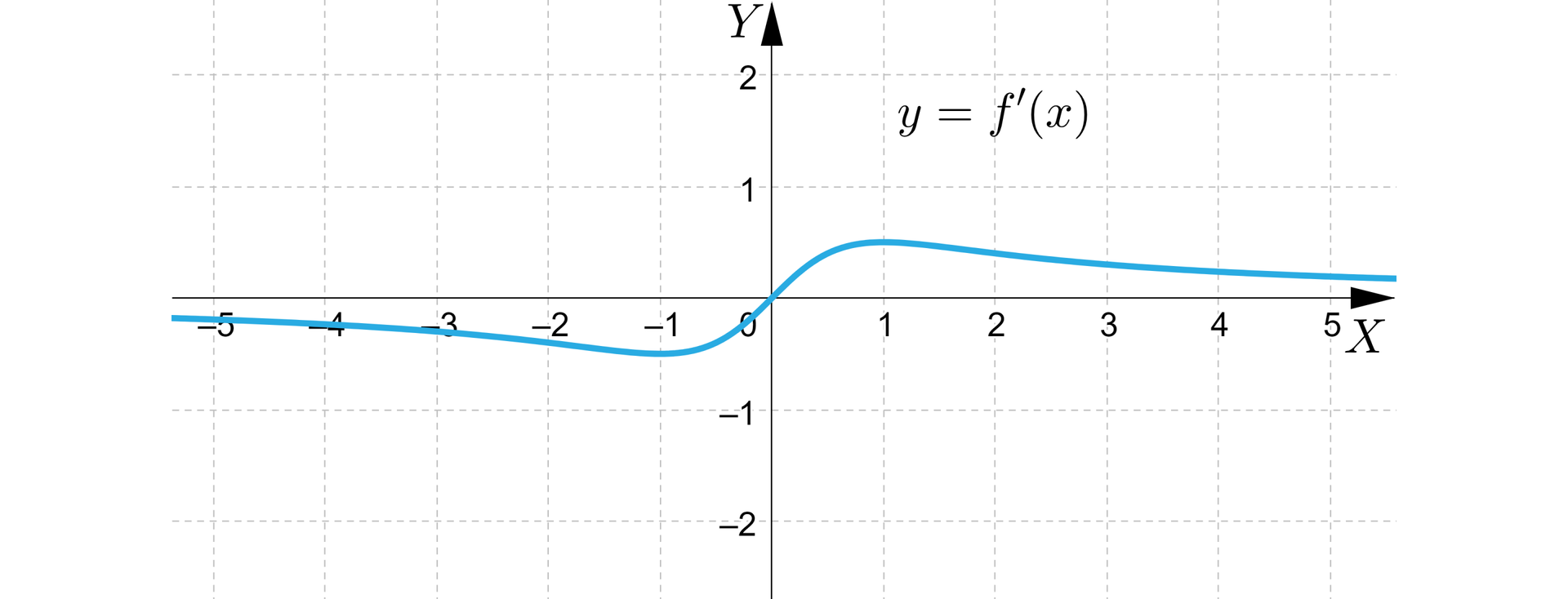
Na rysunku przedstawiony jest układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osią Y od minus dwóch do dwóch. Na układzie współrzędnych zaznaczono wykres funkcji danej wzorem y=f'x. Funkcja f maleje dla argumentów od minus nieskończoności do okolic argumentu minus jeden, ten fragment zawsze przyjmuje wartości ujemne, następnie funkcja w sposób płynny zaczyna rosnąć do okolic argumentu jeden, przechodząc przez punkt nawias zero średnik zero koniec nawiasu. Od okolic argumentu jeden funkcja jest malejąca dla argumentów do minus nieskończoności, ten fragment funkcji zawsze przyjmuje wartości dodatnie.

RNAy2JuSVMiCa

Zaznacz czy zdanie jest prawdziwe czy fałszywe.

Zdanie	Prawda	Fałsz
Funkcja $f$ prawdopodobnie ma ekstremum w puncie $x_{0} = 0$ , bo jej pochodna $f' (0) = 0$ .	□	□
Funkcja $f$ nie posiada ekstremów, bo jej pochodna $f' (x)$ posiada ekstrema.	□	□
Funkcja $f$ posiada dwa ekstrema, bo równanie $f' (x) = 0$ ma dwa rozwiązania.	□	□

Ryac8unxzprA8

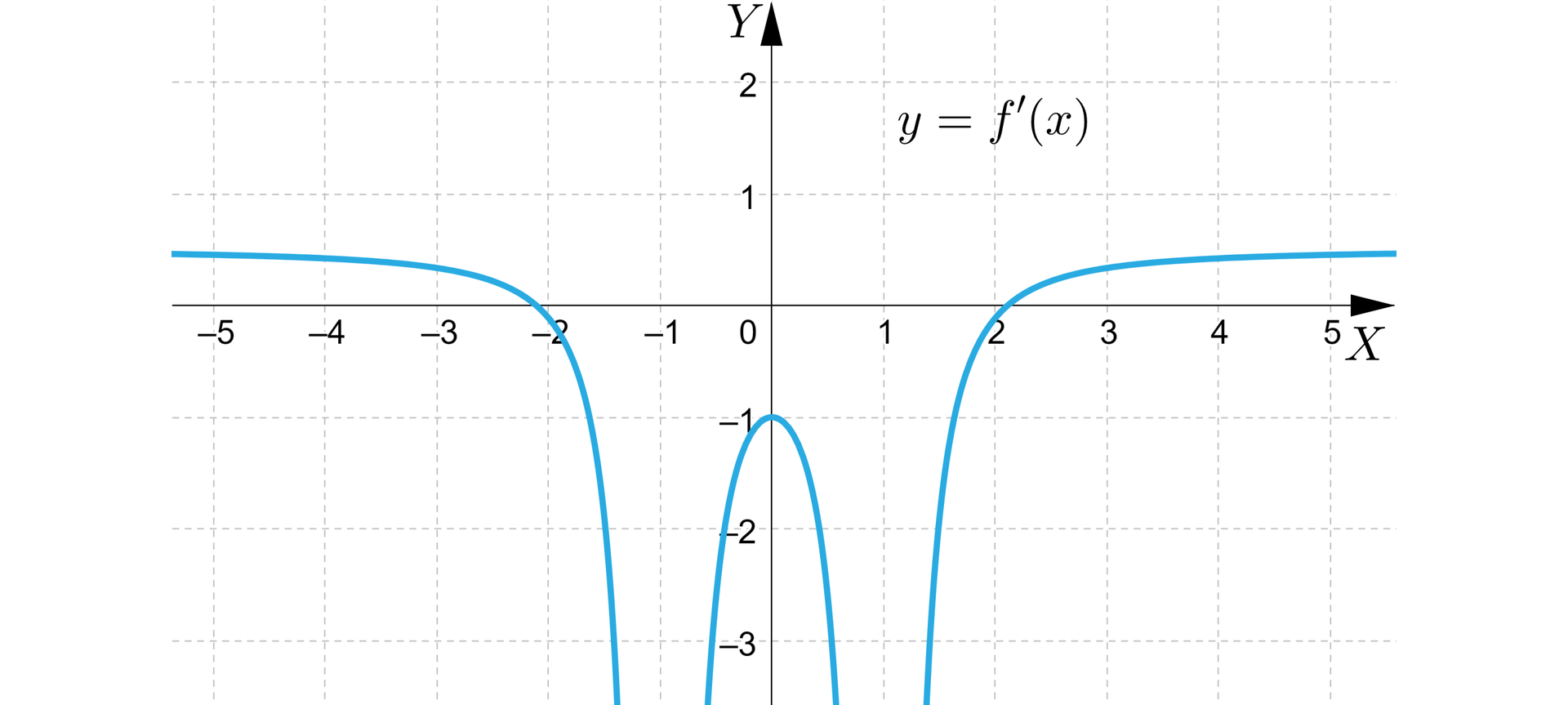
Na rysunku przedstawiony jest układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osią Y od minus trzech do dwóch. W układzie współrzędnych zaznaczono wykres funkcji danej wzorem y=f'x. Funkcja f maleje dla argumentów od minus nieskończoności do okolic argumentu minus jeden, ten fragment jest dodatni dla argumentów od minus nieskończoności do minus dwóch, przechodzi przez punkt nawias minus dwa średnik zero koniec nawiasu, a następnie jest ujemny dla argumentów od minus dwóch do minus jednego, następnie funkcja w sposób płynny zaczyna rosnąć do okolic argumentu zero, przyjmując tylko wartości ujemne. Funkcja przecina oś y w punkcie nawias zero średnik minus jeden koniec nawiasu. Następnie płynnie maleje dla argumentów od zera do jednego, przy czym jej wartości na tym przedziale są ujemne. Funkcja rośnie dla argumentów od jednego do nieskończoności, ten fragment przyjmuje wartości ujemne dla argumentów od jednego do dwóch, przechodzi przez punkt nawias dwa średnik zero koniec nawiasu, a następnie przyjmuje wartości dodatnie dla argumentów od dwóch do nieskończoności.

R1eHdpigHgMou

Łączenie par. Zaznacz czy zdanie jest prawdziwe czy fałszywe.. Funkcja

f

prawdopodobnie ma ekstremum w puncie

x_{0} = 0

, bo jej pochodna

f' (0) = 0

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja

f

prawdopodobnie posiada dwa ekstrema, bo równanie

f' (x) = 0

ma dwa rozwiązania.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja

f

posiada ekstremum w punkcie

x_{0} = 0

, bo pochodna

f' (x)

posiada w tym punkcie ekstremum.. Możliwe odpowiedzi: Prawda, Fałsz

Zaznacz czy zdanie jest prawdziwe czy fałszywe.

Zdanie	Prawda	Fałsz
Funkcja $f$ prawdopodobnie ma ekstremum w puncie $x_{0} = 0$ , bo jej pochodna $f' (0) = 0$ .	□	□
Funkcja $f$ prawdopodobnie posiada dwa ekstrema, bo równanie $f' (x) = 0$ ma dwa rozwiązania.	□	□
Funkcja $f$ posiada ekstremum w punkcie $x_{0} = 0$ , bo pochodna $f' (x)$ posiada w tym punkcie ekstremum.	□	□

Rm8WpFnuStp0x

Na rysunku przedstawiony jest układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osią Y od minus dwóch do dwóch. W układzie współrzędnych zaznaczono wykres funkcji danej wzorem y=f'x. Funkcja f rośnie dla argumentów od minus nieskończoności do okolic argumentu minus, początek ułamka jeden, mianownik dwa, koniec ułamka, ten fragment przyjmuje wartości ujemne dla argumentów od minus nieskończoności do minus jednego, przechodzi przez punkt nawias minus jeden średnik zero koniec nawiasu, a następnie przyjmuje wartości dodatnie dla argumentów od minus jednego do okolic argumentu minus początek ułamka 1, mianownik 2, koniec ułamka, następnie funkcja w sposób płynny zaczyna maleć do okolic argumentu jeden, przyjmując wartości ujemne dla argumentów od okolic argumentu minus początek ułamka 1, mianownik dwa koniec ułamka do zera, przechodzi przez punkt nawias zero średnik zero koniec nawiasu, a następnie przyjmuje wartości ujemne dla argumentów od zera do okolic argumentu jeden. Następnie płynnie rośnie dla argumentów od okolic argumentu jeden do nieskończoności, przy czym ten fragment przyjmuje wartości ujemne dla argumentów od okolic argumentu jeden do dwóch, przechodzi przez punkt nawias dwa średnik zero koniec nawiasu i przyjmuje wartości dodatnie dla argumentów od dwóch do nieskończoności.

RBfIt4Uv97MUA

Łączenie par. Zaznacz czy zdanie jest prawdziwe czy fałszywe.. Funkcja

f

prawdopodobnie ma ekstremum w puncie

x_{0} = 0

, bo jej pochodna

f' (0) = 0

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja

f

prawdopodobnie posiada trzy ekstrema, bo równanie

f' (x) = 0

ma trzy rozwiązania.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja

f

posiada dwa ekstrema, bo pochodna

f' (x)

posiada dwa ekstrema.. Możliwe odpowiedzi: Prawda, Fałsz

Zaznacz czy zdanie jest prawdziwe czy fałszywe.

Zdanie	Prawda	Fałsz
Funkcja $f$ prawdopodobnie ma ekstremum w puncie $x_{0} = 0$ , bo jej pochodna $f' (0) = 0$ .	□	□
Funkcja $f$ prawdopodobnie posiada trzy ekstrema, bo równanie $f' (x) = 0$ ma trzy rozwiązania.	□	□
Funkcja $f$ posiada dwa ekstrema, bo pochodna $f' (x)$ posiada dwa ekstrema.	□	□

Ćwiczenie 2

RwxwT67XjnxYl

Dopasuj do danej funkcji wzór na jej pochodną oraz punkty stacjonarne (jeśli takie posiada).
Przeciągnij właściwe odpowiedzi w poprawne miejsca.

$f (x) = {(x + 2)}^{3} {(x - 1)}^{2}$ , $f (x) = \frac{x}{x + 2}$ dla $x \in ℝ ∖ "{"- 2"}"$ , $f (x) = x^{3} + 3 x^{2} + 3 x - 5$

Wzór funkcji	Wzór pochodnej	Punkty stacjonarne
$f (x) = {(x + 2)}^{3} {(x - 1)}^{2}$
$f (x) = \frac{x}{x + 2}$ dla $x \in ℝ ∖ "{"- 2"}"$
$f (x) = x^{3} + 3 x^{2} + 3 x - 5$

$f' (x) = 3 {(x + 2)}^{2} {(x - 1)}^{2} + 2 {(x + 2)}^{3} (x - 1) = {(x + 2)}^{2} (x - 1) (5 x + 1)$ , ${(x + 2)}^{2} (x - 1) (5 x + 1) = 0$ ; $x = - 2$ ; $x = - 0, 2$ ; $x = 1$ ;

$f' (x) = \frac{x + 2 - x}{{(x + 2)}^{2}} = \frac{2}{{(x + 2)}^{2}}$ , $\frac{2}{{(x + 2)}^{2}} \neq 0$ dla $x \in ℝ ∖ \{- 2\}$ ;

$f' (x) = 3 x^{2} + 6 x + 3 = 3 {(x + 1)}^{2}$ , $3 {(x + 1)}^{2} = 0$ , $x = - 1$ .

R4NDUuvpHGwhY1

Ćwiczenie 3

Dostępne opcje do wyboru: ujemna,

f' (x_{0}) = 0

, stała, wystarczającym, nie istnieje, dodatnia, koniecznym, maksimum, minimum,

f' (x_{0}) > 0

, punktami stacjonarnymi, zeru, istnieje, punkty skrajne, ekstremum,

f' (x_{0}) = f (x)

. Polecenie: Uzupełnij podany tekst przeciągając w odpowiednie miejsca właściwy wyraz. Jeśli funkcja

f (x)

jest różniczkowalna w punkcie

x_{0}

i ma w tym punkcie luka do uzupełnienia , to luka do uzupełnienia . Punkty, w których pochodna funkcji jest równa zeru nazywamy luka do uzupełnienia . Jeśli funkcja

f (x)

jest różniczkowalna w punkcie

x_{0}

f' (x_{0}) \neq 0

to funkcja ta nie ma w tym punkcie ekstremum. Funkcja może mieć ekstremum lokalne jedynie w punktach, w których jej pochodna luka do uzupełnienia albo luka do uzupełnienia i jest równa luka do uzupełnienia . Zerowanie się pochodnej jest warunkiem luka do uzupełnienia istnienia ekstremum lokalnego dla funkcji różniczkowalnej, ale nie jest warunkiem luka do uzupełnienia .

Uzupełnij podany tekst przeciągając w odpowiednie miejsca właściwy wyraz.

$f' (x_{0}) = f (x)$ , wystarczającym, $f' (x_{0}) > 0$ , zeru, dodatnia, nie istnieje, maksimum, ekstremum, minimum, punktami stacjonarnymi, $f' (x_{0}) \neq 0$ , koniecznym, ujemna, istnieje, $f' (x_{0}) = 0$ , stała, punkty skrajne

Jeśli funkcja $f (x)$ jest różniczkowalna w punkcie $x_{0}$ i ma w tym punkcie , to . Punkty, w których pochodna funkcji jest równa zeru nazywamy . Jeśli funkcja $f (x)$ jest różniczkowalna w punkcie $x_{0}$ i to funkcja ta nie ma w tym punkcie ekstremum. Funkcja może mieć ekstremum lokalne jedynie w punktach, w których jej pochodna albo i jest równa . Zerowanie się pochodnej jest warunkiem istnienia ekstremum lokalnego dla funkcji różniczkowalnej, ale nie jest warunkiem .

Ćwiczenie 4

Sprawdź, czy funkcja $f (x) = 3 x^{4} + x^{3} + 4 x^{2} + 2 x - 1$ może mieć w punktach $x_{1} = 1$ , $x_{2} = - \frac{1}{4}$ , $x_{3} = - \frac{2}{3}$ ekstremum, a w których na pewno nie ma.

Funkcja $f (x)$ jako wielomian jest różniczkowalna w zbiorze $ℝ$ .

Jej pochodna dana jest wzorem $f' (x) = 12 x^{3} + 3 x^{2} + 8 x + 2 = 3 x^{2} (4 x + 1) + 2 (4 x + 1) = (4 x + 1) (3 x^{2} + 2)$ .

Na mocy Twierdzenia o warunku koniecznym istnienia ekstremum, funkcja różniczkowalna $f (x)$ może mieć ekstremum w punkcie, wtedy i tylko, gdy jej pochodna w tym punkcie jest równa zeru.

Sprawdźmy, kiedy pochodna $f' (x) = 0$ . Otrzymujemy kolejno:

$f' (x) = 0$ , gdy $(4 x + 1) (3 x^{2} + 2) = 0$ , czyli $x = - \frac{1}{4}$ .

Stąd rozważana funkcja $f (x)$ może mieć (ale nie musi) ekstremum tylko w punkcie $x_{2} = - \frac{1}{4}$ , a na pewno nie ma ich w punktach $x_{1} = 1$ , $x_{3} = - \frac{2}{3}$ .

Ćwiczenie 5

Sprawdź, w jakich punktach funkcja $f (x) = \frac{x^{2}}{x^{2} - 1}$ , $x \in ℝ ∖ \{- 1, 1\}$ mogłaby mieć ekstremum.

Dziedziną funkcji jest zbiór $ℝ ∖ \{- 1, 1\}$ .

Funkcja $f (x)$ jako funkcja wymierna jest różniczkowalna w całej dziedzinie.

Jej pochodna dana jest wzorem

$f' (x) = \frac{2 x (x^{2} - 1) - x^{2} \cdot 2 x}{{(x^{2} - 1)}^{2}} = \frac{- 2 x}{{(x^{2} - 1)}^{2}}$ .

Sprawdzamy, kiedy spełniony jest warunek konieczny istnienia ekstremum, czyli kiedy pochodna $f' (x) = 0$ . Otrzymujemy kolejno:

$f' (x) = 0$ , gdy $\frac{- 2 x}{{(x^{2} - 1)}^{2}} = 0$ , czyli $- 2 x = 0$ , stąd $x = 0$ .

Punkt $x = 0$ jest punktem stacjonarnym, czyli takim w którym funkcja $f$ może (ale nie musi) mieć ekstremum.

Ćwiczenie 6

Uzasadnij, że funkcja $f (x) = \frac{x^{2} - 3 x}{x^{2} - 1}$ nie ma ekstremum.

Dziedziną funkcji jest zbiór $D_{f} = ℝ ∖ \{- 1, 1\}$ .

Funkcja $f (x)$ jako funkcja wymierna jest różniczkowalna w całej dziedzinie.

Jej pochodna dana jest wzorem $f' (x) = \frac{3 x^{2} - 2 x + 3}{{(x^{2} - 1)}^{2}}$ , $D_{f'} = D_{f}$ . Mamy

$\frac{3 x^{2} - 2 x + 3}{{(x^{2} - 1)}^{2}} \neq 0$ , $Δ < 0$ , dla każdego argumentu ze zbioru $ℝ ∖ \{- 1, 1\}$ .

Zatem nie jest spełniony warunek konieczny istnienia ekstremum funkcji, czyli nie ma takiego punktu $x_{0} \in D_{f}$ , dla którego pochodna $f' (x_{0}) = 0$ . Stąd rozważana funkcja $f$ nie ma ekstremum.

Ćwiczenie 7

Dla jakich wartości parametru $p$ funkcja $f (x) = \frac{1}{4} x^{4} + \frac{1}{3} (p + 3) x^{3} + 2 p x^{2}$ ma dokładnie jeden punkt stacjonarny.

Funkcja $f (x)$ jako wielomian jest różniczkowalna w zbiorze $ℝ$ .

Jej pochodna dana jest wzorem $f' (x) = x^{3} + (p + 3) x^{2} + 4 p x = x [x^{2} + (p + 3) x + 4 p]$ .

Na mocy Twierdzenia o warunku koniecznym istnienia ekstremum funkcji wiemy, że funkcja ma punkty stacjonarne, wtedy i tylko wtedy, gdy $f' (x) = 0$ .

Z treści zadania wynika, że funkcja $f$ ma mieć tylko jeden punkt stacjonarny.

Zatem równanie

$f' (x) = 0$ , czyli $x [x^{2} + (p + 3) x + 4 p] = 0$ powinno mieć tylko jedno rozwiązanie.

Dostajemy wówczas, że

$x = 0$ oraz $x^{2} + (p + 3) x + 4 p \neq 0$ .

Taki warunek wynika z faktu, że wyrażenie w nawiasie nie może mieć innych pierwiastków niż już znaleziony tzn. $x = 0$ . Wówczas

$x^{2} + (p + 3) x + 4 p \neq 0$ , gdy $Δ < 0$ .

$Δ = {(p + 3)}^{2} - 16 p = (p - 1) (p - 9) < 0$ , dla $p \in (1, 9)$ .

Zatem rozważana funkcja $f$ posiada tylko jeden punkt stacjonarny dla $p \in (1, 9)$ .

Ćwiczenie 8

Dla jakich wartości parametru $m$ funkcja $f (x) = \frac{1}{3} (m^{2} - 1) x^{3} + (m - 1) x^{2} + 2 x$ nie ma punktów stacjonarnych.

Funkcja $f (x)$ jako wielomian jest różniczkowalna w zbiorze $ℝ$ .

Zbadamy ilość punktów stacjonarnych

dla $m = 1$ mamy $f (x) = 2 x$ , $f' (x) = 2 \neq 0$ , czyli brak punktów stacjonarnych,

dla $m = - 1$ mamy $f (x) = - 2 x^{2} + 2 x$ , $f' (x) = - 4 x + 2 = 0$ , dla $x = 0, 5$ , czyli funkcja ma jeden punkt stacjonarny, co jest sprzeczne z warunkami zadania,

dla $m \neq 1$ i $m \neq - 1$ mamy kolejno $f' (x) = (m^{2} - 1) x^{2} + 2 (m - 1) x + 2$ .

Na mocy Twierdzenia o warunku koniecznym istnienia ekstremum funkcji wiemy, że funkcja ma punkty stacjonarne, wtedy i tylko wtedy, gdy $f' (x) = 0$ .

Z treści zadania wynika, że funkcja $f$ ma nie mieć punktów stacjonarnych.

Zatem równanie $f' (x) = 0$ powinno nie mieć rozwiązań, czyli $Δ < 0$ . Otrzymujemy

$Δ = 4 {(m - 1)}^{2} - 8 (m^{2} - 1) = - 4 (m + 3) (m - 1) < 0$

dla $m \in (- \infty, - 3) \cup (1, \infty)$ .

Ostatecznie, rozważana funkcja nie ma punktów stacjonarnych dla $m \in (- \infty, - 3) \cup ⟨1, \infty)$ .

Prezentacja multimedialna

Dla nauczyciela