Prezentacja multimedialna
Polecenie 1
Zapoznaj się z prezentacją multimedialną, a następnie wykonaj ćwiczenia zamieszczone poniżej.
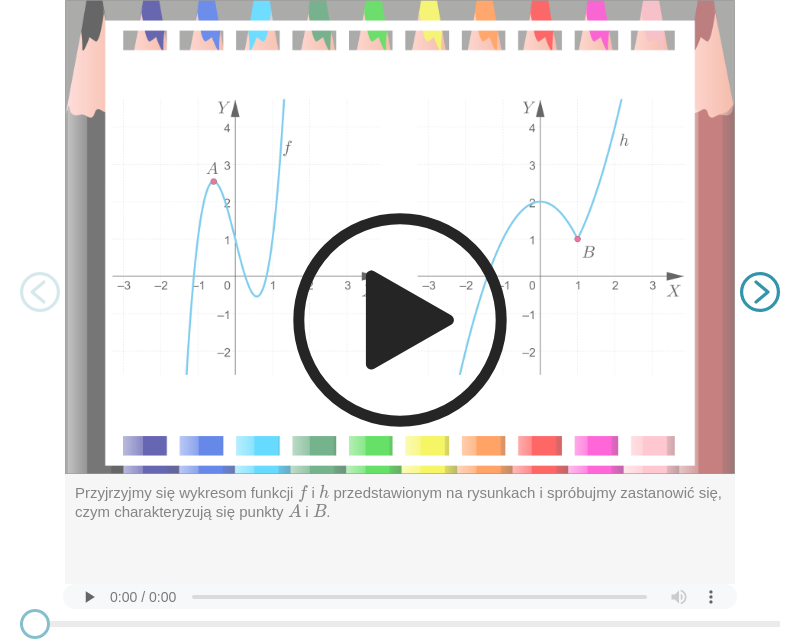
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DUtuUFZE6
Polecenie 2
Łączenie par. Na podstawie informacji zawartych w filmie zaznacz czy zdanie jest prawdziwe czy fałszywe.. Na to aby funkcja posiadała ekstremum w danym punkcie potrzeba i wystarcza, aby jej pochodna w tym punkcie była różna od zera.. Możliwe odpowiedzi: Prawda, Fałsz. Zerowanie się pochodnej jest warunkiem koniecznym istnienia ekstremum lokalnego dla funkcji różniczkowalnej, ale nie jest warunkiem wystarczającym.. Możliwe odpowiedzi: Prawda, Fałsz. Jeśli funkcja jest różniczkowalna w punkcie i , to funkcja ta nie ma w tym punkcie ekstremum.. Możliwe odpowiedzi: Prawda, Fałsz. Wszystkie punkty dla których nazywamy punktami stacjonarnymi.. Możliwe odpowiedzi: Prawda, Fałsz
Na podstawie informacji zawartych w prezentacji multimedialnej zaznacz czy zdanie jest prawdziwe czy fałszywe.
| Zdanie | Prawda | Fałsz |
| Na to aby funkcja posiadała ekstremum w danym punkcie potrzeba i wystarcza, aby jej pochodna w tym punkcie była różna od zera. | □ | □ |
| Zerowanie się pochodnej jest warunkiem koniecznym istnienia ekstremum lokalnego dla funkcji różniczkowalnej, ale nie jest warunkiem wystarczającym. | □ | □ |
| Jeśli funkcja jest różniczkowalna w punkcie i , to funkcja ta nie ma w tym punkcie ekstremum. | □ | □ |
| Wszystkie punkty dla których nazywamy punktami stacjonarnymi. | □ | □ |
Polecenie 3
Wyznaczymy punkty, w których funkcja może (ale nie musi) mieć ekstrema.