Przeczytaj
Jeśli funkcja jest różniczkowalna w punkcie i ma w tym punkcie ekstremum, to
Punkty, w których pochodna funkcji jest równa zeru nazywamy punktami stacjonarnymi.
Twierdzenie odwrotne jest fałszywe.
Na przykład funkcja , ma pochodną w punkcie równą zeru i nie ma w tym punkcie ekstremum.
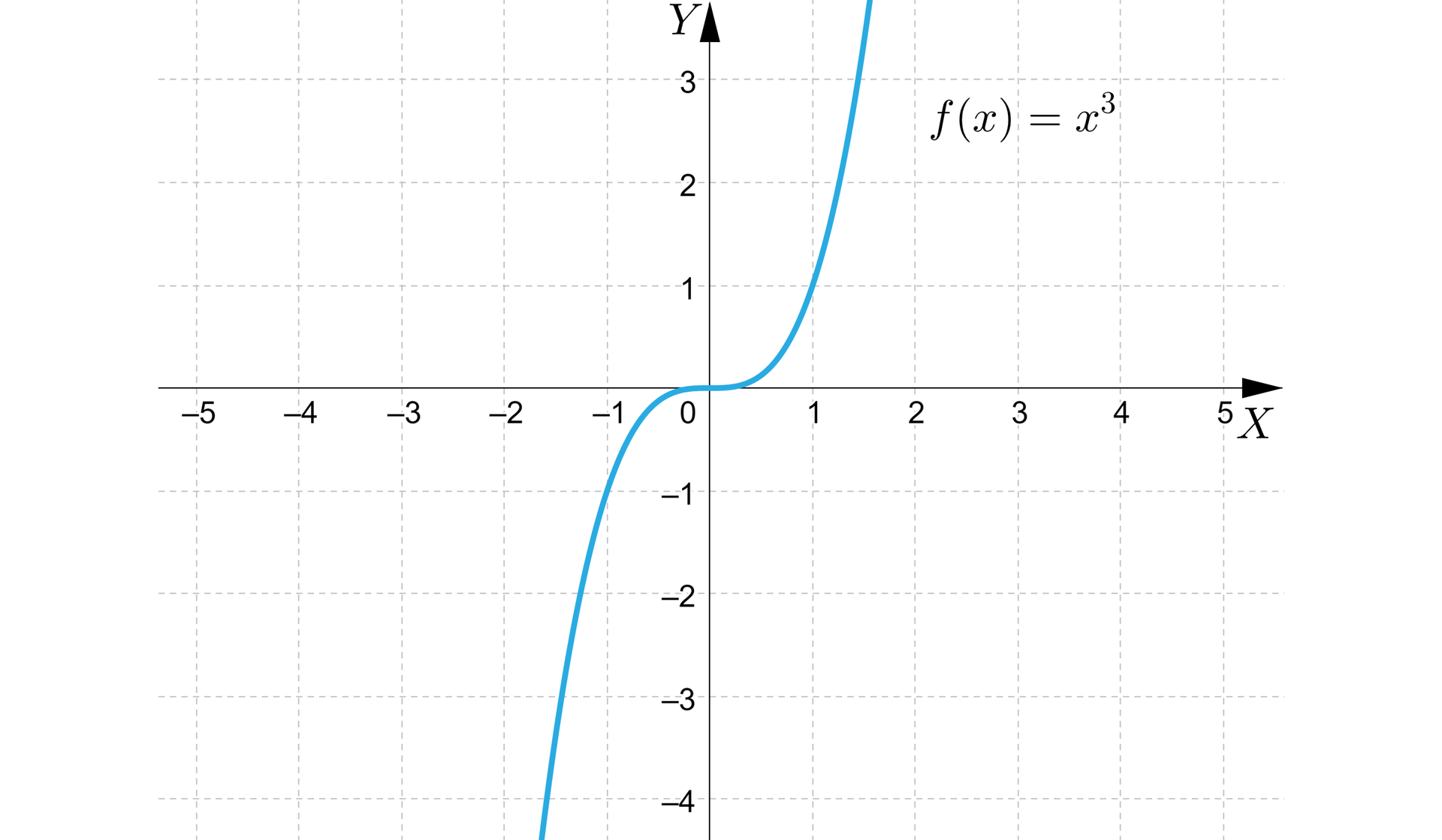
Zerowanie się pochodnej jest warunkiem koniecznym istnienia ekstremum lokalnego dla funkcji różniczkowalnej, ale nie jest warunkiem wystarczającym.
Jeśli funkcja jest różniczkowalna w punkcie i , to funkcja ta nie ma w tym punkcie ekstremum. Funkcja może mieć ekstremum lokalne jedynie w punktach, w których jej pochodna nie istnieje albo istnieje i jest równa zeru.
Sprawdzimy, w którym z punktów: , , , funkcja może mieć ekstremum, a w którym na pewno nie ma.
Rozwiązanie:
Funkcja jako wielomian jest różniczkowalna w zbiorze . Jej pochodna dana jest wzorem .
Na mocy pierwszego twierdzenia o warunku koniecznym istnienia ekstremum, funkcja różniczkowalnafunkcja różniczkowalna może mieć ekstremum w punkcie, wtedy i tylko, gdy jej pochodna jest w tym punkcie równa zeru.
Sprawdźmy, kiedy pochodna . Otrzymujemy kolejno:
, gdy , czyli lub .
Stąd rozważana funkcja może mieć (ale nie musi) ekstremum tylko w punktach , , a na pewno nie ma ich w punktach , .
Sprawdzimy w jakich punktach funkcja mogłaby mieć ekstremum.
Rozwiązanie:
Dziedziną funkcji jest zbiór . Funkcja jako funkcja wymierna jest różniczkowalna w całej dziedzinie. Jej pochodna dana jest wzorem
.
Sprawdzamy, kiedy spełniony jest warunek konieczny istnienia ekstremum, czyli kiedy pochodna . Otrzymujemy kolejno:
, gdy , czyli , stąd .
Punkt jest punktem stacjonarnym, czyli takim w którym funkcja może (ale nie musi) mieć ekstremum.
Uzasadnimy, że funkcja nie ma ekstremum.
Rozwiązanie:
Dziedziną funkcji jest zbiór .
Funkcja jako funkcja wymierna jest różniczkowalna w całej dziedzinie. Jej pochodna dana jest wzorem dla każdego argumentu ze zbioru .
Zatem nie jest spełniony warunek konieczny istnienia ekstremum funkcji, czyli nie ma takiego punktu , dla którego pochodna .
Stąd rozważana funkcja nie ma ekstremum.
Sprawdzimy, dla jakiego parametru funkcja nie ma punktów stacjonarnych.
Rozwiązanie:
Funkcja jako wielomian jest różniczkowalna w zbiorze .
Jej pochodna dana jest wzorem .
Na mocy Twierdzenia o warunku koniecznym istnienia ekstremum funkcji wiemy, że funkcja nie ma punktów stacjonarnych, wtedy i tylko wtedy, gdy . Otrzymujemy kolejno
, gdy , czyli ,
, wtedy i tylko wtedy, gdy .
Zatem rozważana funkcja nie posiada punktów stacjonarnych dla .
Znajdziemy te wartości parametru , dla których funkcja ma dwa punkty stacjonarne.
Rozwiązanie:
Funkcja jako wielomian jest różniczkowalna w zbiorze .
Jej pochodna dana jest wzorem .
Na mocy Twierdzenia o warunku koniecznym istnienia ekstremum funkcji wiemy, że funkcja ma punkty stacjonarne, wtedy i tylko wtedy, gdy .
Mamy zatem .
Z warunków zadania wynika, że równanie to ma mieć dwa rozwiązania, czyli . Otrzymujemy kolejno
.
Stąd .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DardqW9ID
Słownik
funkcję nazywamy różniczkowalną jeśli ma pochodną w każdym punkcie dziedziny