Sprawdź się

1
Pokaż ćwiczenia:
1
Ćwiczenie 1
R1TrWtTslk00Y
Wymyśl pytanie na kartkówkę związane z tematem materiału.
RfiboommROQVN
Wymyśl pytanie na kartkówkę związane z tematem materiału.
R1Fglwr5Hy9jR1
Ćwiczenie 2
Wskaż zbiór rozwiązań nierówności 2x-3≤17. Możliwe odpowiedzi: 1. x∈-7,10, 2. x∈-7,10, 3. x∈-∞,-7∪10,+∞, 4. x∈-∞,-7∪10,+∞
Rjg6tlhj4FpBX2
Ćwiczenie 3
Rozwiąż nierówność 2x-5≤x+8.
Przeciągnij odpowiednie symbole tak, aby poniżej pojawił się zapis rozwiązania danej nierówności. Odpowiedź: x∈ 1. ), 2. +∞, 3. -1, 4. ⟨, 5. -13, 6. 1, 7. 13, 8. -∞, 9. (, 10. ⟩1. ), 2. +∞, 3. -1, 4. ⟨, 5. -13, 6. 1, 7. 13, 8. -∞, 9. (, 10. ⟩,1. ), 2. +∞, 3. -1, 4. ⟨, 5. -13, 6. 1, 7. 13, 8. -∞, 9. (, 10. ⟩1. ), 2. +∞, 3. -1, 4. ⟨, 5. -13, 6. 1, 7. 13, 8. -∞, 9. (, 10. ⟩
2
Ćwiczenie 4

Poniższy rysunek przedstawia zbiór wszystkich liczb rzeczywistych, które spełniają nierówność 3x-n<1410.

RdqZgbhwPjePC
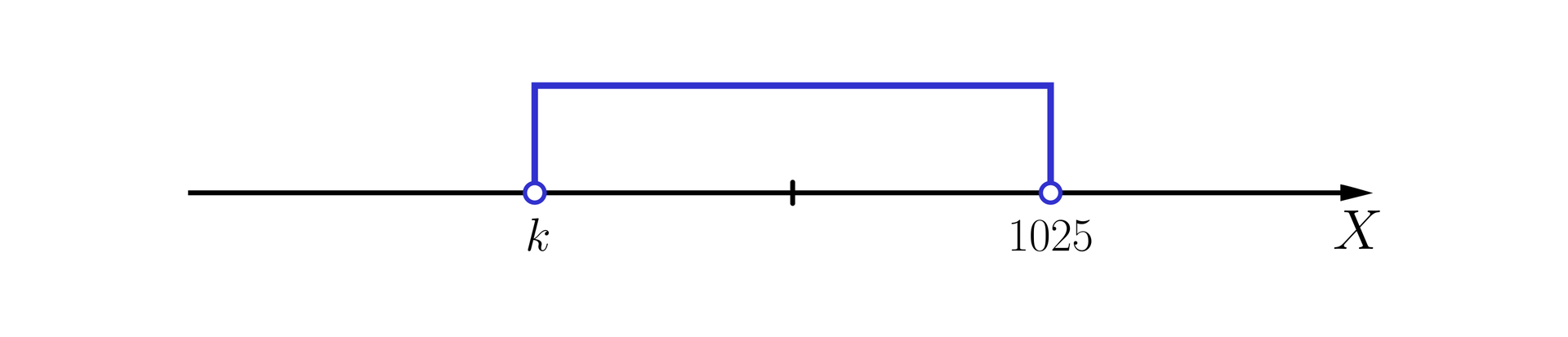
Ilustracja przedstawia poziomą oś X. Z lewej strony na osi zaznaczono niezamalowany punkt k, z prawej niezamalowany punkt o współrzędnej 1025, a pomiędzy punktami zaznaczono na osi krótką pionową kreskę. Dodatkowo zaznaczono przedział otwarty od k do 1025
RT9gYV64A2W3m
Oblicz n oraz k . Odpowiedź: n= Tu uzupełnij, k= Tu uzupełnij.
R126l7QiCVIyt2
Ćwiczenie 5
Rozpatrzmy nierówność
x-12-x+5≤7-x.
Oznaczmy przez:
m – największą ujemną liczbę całkowitą, która spełnia tę nierówność,
k – największą dodatnią liczbę całkowitą, która spełnia tę nierówność.
Oblicz k·m. Zakoduj poniżej kolejno cyfry: setek, dziesiątek i jedności otrzymanego wyniku. Odpowiedź: Tu uzupełnij Tu uzupełnij Tu uzupełnij
21
Ćwiczenie 6
R79vzA0PG9bfj
Wybierz jedno nowe słowo poznane podczas dzisiejszej lekcji i ułóż z nim zdanie.
R1AwfrR44OAAN
Uzupełnij luki, dobierając odpowiednie zbiory rozwiązań do podanych nierówności.
  • Zbiorem rozwiązań nierówności x+5-2≤10 jest zbiór 1. zbiór domknięty od minus trzynastu do trzech, 2. suma zbiorów domkniętych: zbiór pierwszy od minus siedemnastu do minus trzynastu, zbiór drugi od trzech do siedmiu, 3. suma zbiorów domkniętych: zbiór pierwszy od minus trzynastu do minus dziewięciu, zbiór drugi minus jeden do trzech, 4. zbiór domknięty od minus siedemnastu do siedmiu.

  • Zbiorem rozwiązań nierówności x+5-10≤2 jest zbiór 1. zbiór domknięty od minus trzynastu do trzech, 2. suma zbiorów domkniętych: zbiór pierwszy od minus siedemnastu do minus trzynastu, zbiór drugi od trzech do siedmiu, 3. suma zbiorów domkniętych: zbiór pierwszy od minus trzynastu do minus dziewięciu, zbiór drugi minus jeden do trzech, 4. zbiór domknięty od minus siedemnastu do siedmiu.

  • Zbiorem rozwiązań nierówności x+5-2≤6 jest zbiór 1. zbiór domknięty od minus trzynastu do trzech, 2. suma zbiorów domkniętych: zbiór pierwszy od minus siedemnastu do minus trzynastu, zbiór drugi od trzech do siedmiu, 3. suma zbiorów domkniętych: zbiór pierwszy od minus trzynastu do minus dziewięciu, zbiór drugi minus jeden do trzech, 4. zbiór domknięty od minus siedemnastu do siedmiu.

  • Zbiorem rozwiązań nierówności x+5-6≤2 jest zbiór 1. zbiór domknięty od minus trzynastu do trzech, 2. suma zbiorów domkniętych: zbiór pierwszy od minus siedemnastu do minus trzynastu, zbiór drugi od trzech do siedmiu, 3. suma zbiorów domkniętych: zbiór pierwszy od minus trzynastu do minus dziewięciu, zbiór drugi minus jeden do trzech, 4. zbiór domknięty od minus siedemnastu do siedmiu.
Rjooipk85k4e43
Ćwiczenie 7
Spośród podanych poniżej wybierz i zaznacz te wartości parametru m, dla których nierówność
3x-8+2x-9+5x+10≥m
jest prawdziwa dla każdej liczby rzeczywistej x. Możliwe odpowiedzi: 1. m=25, 2. m=27, 3. m=29, 4. m=31
R1vnixKHI1PKd3
Ćwiczenie 8
Rozpatrzmy nierówność
x-125+x+238<501.
Oznaczmy przez:
k - najmniejszą liczbę całkowitą, która spełnia tę nierówność,
n - największą liczbę całkowitą, która spełnia tę nierówność, .
Wówczas: Możliwe odpowiedzi: 1. k+n=499, 2. n-k=501, 3. 2n+k=82, 4. istnieją takie dodatnie liczby całkowite a i b , dla których zachodzi równość ak+bn=1
Test samosprawdzający
Dla nauczyciela