Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

R16XlkZnLWZPO

Ćwiczenie 2

RU8IhAW4yWq2h

Połącz w pary odpowiadające sobie położenie dwóch okręgów z liczbą punktów wspólnych tych okręgów:

brak punktów wspólnych, nieskończenie wiele punktów wspólnych, dwa punkty wspólne, jeden punkt wspólny

okręgi przecinające się
okręgi rozłączne
okręgi styczne
okręgi pokrywające się

Ćwiczenie 3

RJqfolv16m8Rb

Pogrupuj elementy, zgodnie z podanym opisem. Równania okręgów, które są styczne: Możliwe odpowiedzi: 1.

x^{2} + {(y - 1)}^{2} = 1

oraz

{(x + 2)}^{2} + {(y - 1)}^{2} = 16

, 2.

{(x - 3)}^{2} + {(y - 1)}^{2} = 1

oraz

{(x + 2)}^{2} + {(y - 1)}^{2} = 16

, 3.

{(x - 3)}^{2} + {(y - 1)}^{2} = 1

oraz

{(x + 2)}^{2} + {(y - 1)}^{2} = 4

, 4.

{(x - 3)}^{2} + {(y - 1)}^{2} = 1

oraz

{(x - 3)}^{2} + {(y - 4)}^{2} = 4

Równania okręgów, które są rozłączne: Możliwe odpowiedzi: 1.

x^{2} + {(y - 1)}^{2} = 1

oraz

{(x + 2)}^{2} + {(y - 1)}^{2} = 16

, 2.

{(x - 3)}^{2} + {(y - 1)}^{2} = 1

oraz

{(x + 2)}^{2} + {(y - 1)}^{2} = 16

, 3.

{(x - 3)}^{2} + {(y - 1)}^{2} = 1

oraz

{(x + 2)}^{2} + {(y - 1)}^{2} = 4

, 4.

{(x - 3)}^{2} + {(y - 1)}^{2} = 1

oraz

{(x - 3)}^{2} + {(y - 4)}^{2} = 4

Ćwiczenie 4

R1tafM3AIR6As

Uzupełnij tekst. Jeżeli środkami okręgów są punkty o współrzędnych

S_{1} = (4, 4)

S_{2} = (0, 0)

, a promienie tych okręgów mają długości odpowiednio

r_{1} = 2

oraz

r_{2} = 3

, to okręgi te są 1. stycznie wewnętrznie, 2. rozłączne zewnętrznie, 3. styczne zewnętrznie, 4. rozłączne wewnętrznie.
Jeżeli środkami okręgów są punkty o współrzędnych

S_{1} = (2, 0)

S_{2} = (1, 0)

, a promienie tych okręgów mają długości odpowiednio

r_{1} = 2

oraz

r_{2} = 3

, to okręgi te są 1. stycznie wewnętrznie, 2. rozłączne zewnętrznie, 3. styczne zewnętrznie, 4. rozłączne wewnętrznie.

Uzupełnij tekst.

stycznie wewnętrznie, rozłączne wewnętrznie, rozłączne zewnętrznie, styczne zewnętrznie

Jeżeli środkami okręgów są punkty o współrzędnych $S_{1} = (4, 4)$ i $S_{2} = (0, 0)$ , a promienie tych okręgów mają długości odpowiednio $r_{1} = 2$ oraz $r_{2} = 3$ , to okręgi te są .................................................
Jeżeli środkami okręgów są punkty o współrzędnych $S_{1} = (2, 0)$ i $S_{2} = (1, 0)$ , a promienie tych okręgów mają długości odpowiednio $r_{1} = 2$ oraz $r_{2} = 3$ , to okręgi te są .................................................

Ćwiczenie 5

R11b4nDI5ZMWx

Uzupełnij tekst odpowiednimi liczbami. Dane są okręgi o równaniach

{(x - 2)}^{2} + {(y + 3)}^{2} = 4

oraz

{(x - 2)}^{2} + y^{2} = 9

. Promienie tych okręgów wynoszą odpowiednio:

r_{1} =

Tu uzupełnij

r_{2} =

Tu uzupełnij

r_{1} + r_{2} =

Tu uzupełnij

|r_{2} - r_{1}| =

Tu uzupełnij Odległość między środkami

S_{1}

S_{2}

tych okręgów wynosi Tu uzupełnij. Ponieważ

|S_{1} S_{2}| >

Tu uzupełnij oraz

|S_{1} S_{2}| <

Tu uzupełnij, zatem okręgi przecinają się w dwóch punktach.

Ćwiczenie 6

Przyjrzyj się okręgom na rysunku poniżej, a następnie wybierz zdania opisujące ich wzajemne położenie.

RUTjL7H1BWNup

RaFujRNVxmZAw

R4hzQLSW0sDA9

Ćwiczenie 7

R11ndXK8Wrmt3

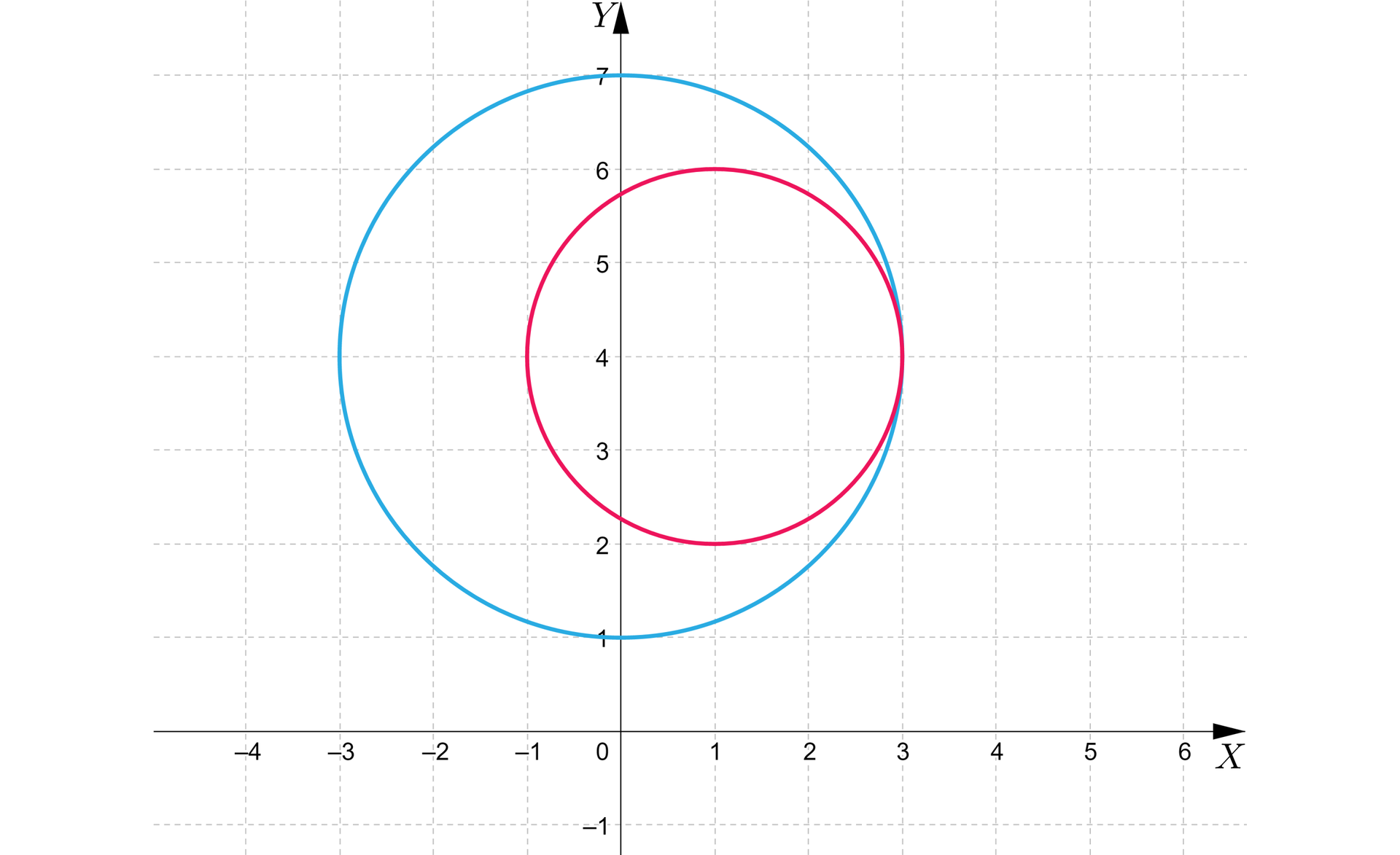
Rozwiąż krzyżówkę.

Odcinek łączący środek okręgu z dowolnym punktem na okręgu.
Jedna z postaci równania okręgu.
Punkt, który leży w połowie średnicy koła.
Okręgi, które nie mają punktów wspólnych.
Mierzona pomiędzy środkami dwóch okręgów.

1
2
3
4
5

Ćwiczenie 8

Dane są dwa okręgi na płaszczyźnie kartezjańskiej o równaniach $x^{2} + {(y - 1)}^{2} = 1$ oraz $x^{2} + {(y - 3)}^{2} = m^{2}$ . Dla jakiej wartości parametru $m$ $(m > 0)$ okręgi są:

a) styczne wewnętrznie

b) rozłączne wewnętrznie

Z podanych równań okręgów możemy odczytać ich środki oraz promienie:

$S_{1} = (0, 1)$ i $r_{1} = 1$ ,

$S_{2} = (0, 3)$ i $r_{2} = m$ .

Obliczmy odległość między środkami tych okręgów:

$|S_{1} S_{2}| = \sqrt{{(3 - 1)}^{2}} = 2$ .

a) jeżeli okręgi są styczne wewnętrznie, to $|S_{1} S_{2}| = |r_{2} - r_{1}|$ , zatem do wyznaczenia wartości parametru $m$ rozwiązujemy równanie:

$2 = |m - 1|$ .

Równanie sprowadzamy do postaci $2 = m - 1$ lub $- 2 = m - 1$ .

Zatem $m = 3$ lub $m = - 1$ .

Ponieważ z założenia $m > 0$ , zatem $m = 3$ .

b) jeżeli okręgi są rozłączne wewnętrznie, to $|S_{1} S_{2}| < |r_{2} - r_{1}|$ , zatem do wyznaczenia wartości parametru $m$ rozwiązujemy nierówność:

$2 < |m - 1|$ .

Nierównosć jest równoważna nierównościom $m - 1 > 2$ lub $m - 1 < - 2$ .

Zatem $m > 3$ lub $m < - 1$ .

Ponieważ z założenia $m > 0$ , zatem $m > 3$ .

Aplet

Dla nauczyciela