Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Rozważmy dwa okręgi. Pary punktów $P$ , $Q$ oraz $R$ , $S$ leżą odpowiednio na dwóch wspólnych stycznych zewnętrznych do tych okręgów, jak na rysunku.

R1A3UVzQp0bkX

Na ilustracji przedstawiono dwa okręgi. Poprowadzono dwie proste. Pierwsza prosta jest styczna do pierwszego okręgu w punkcie P, oraz do drugiego w punkcie Q. Druga prosta jest styczna do okręgu pierwszego w punkcie R, oraz do drugiego w punkcie S. Połączono punkt R z punktem Q. Odcinek RQ przecina okrąg pierwszy w punkcie B, oraz okrąg drugi w punkcie A.

Przez punkty $Q$ i $R$ poprowadzono prostą, która przecięła te okręgi odpowiednio w punktach $A$ i $B$ . Wykaż, że $|A Q| = |B R|$ .

Korzystając z potęgi punktu względem okręgu możemy zapisać: $|Q R| \cdot |Q B| = {|P Q|}^{2}$ oraz $|Q R| \cdot |A R| = {|R S|}^{2}$ . Ale $|Q B| = |A Q| + |A B|$ oraz $|A R| = |B R| + |A B|$ . Ponieważ odcinki stycznych $R S$ i $P Q$ są równe, więc $|Q R| \cdot (|A Q| + |A B|) = |Q R| \cdot (|B R| + |A B|)$ . Stąd $|A Q| = |B R|$ .

Ćwiczenie 2

Wykaż równość odcinków $A P$ i $B P$ , wyznaczonych na stycznych do trzech przecinających się okręgów, poprowadzonych z punktu przecięcia się dwóch siecznych $R S$ i $M N$ , jak na poniższym rysunku.

Rd8iM0uydirpe

Na ilustracji przedstawiono trzy okręgi. Pierwszy okręg, przecina się z drugim w punktach R i S. Drugi okrąg przecina się z trzecim w punktach M i N. Poprowadzono proste RS, oraz MN, przecinające się w punkcie P, znajdującym się nad okręgami. Punkt P połączono z punktem A, znajdującym się na pierwszym okręgu, oraz z punktem B, znajdującym się na na okręgu trzecim. Punkty A i B znajdują się w górnych częściach okręgów.

Wystarczy trzykrotnie skorzystać z twierdzenia o stycznej i siecznej. Mamy: $|P S| \cdot |P R| = {|P A|}^{2}$ , $|P S| \cdot |P R| = |P N| \cdot |P M|$ oraz $|P N| \cdot |P M| = {|P B|}^{2}$ . Korzystając z przechodniości relacji równości mamy: ${|P A|}^{2} = {|P B|}^{2}$ . Stąd teza.

Ćwiczenie 3

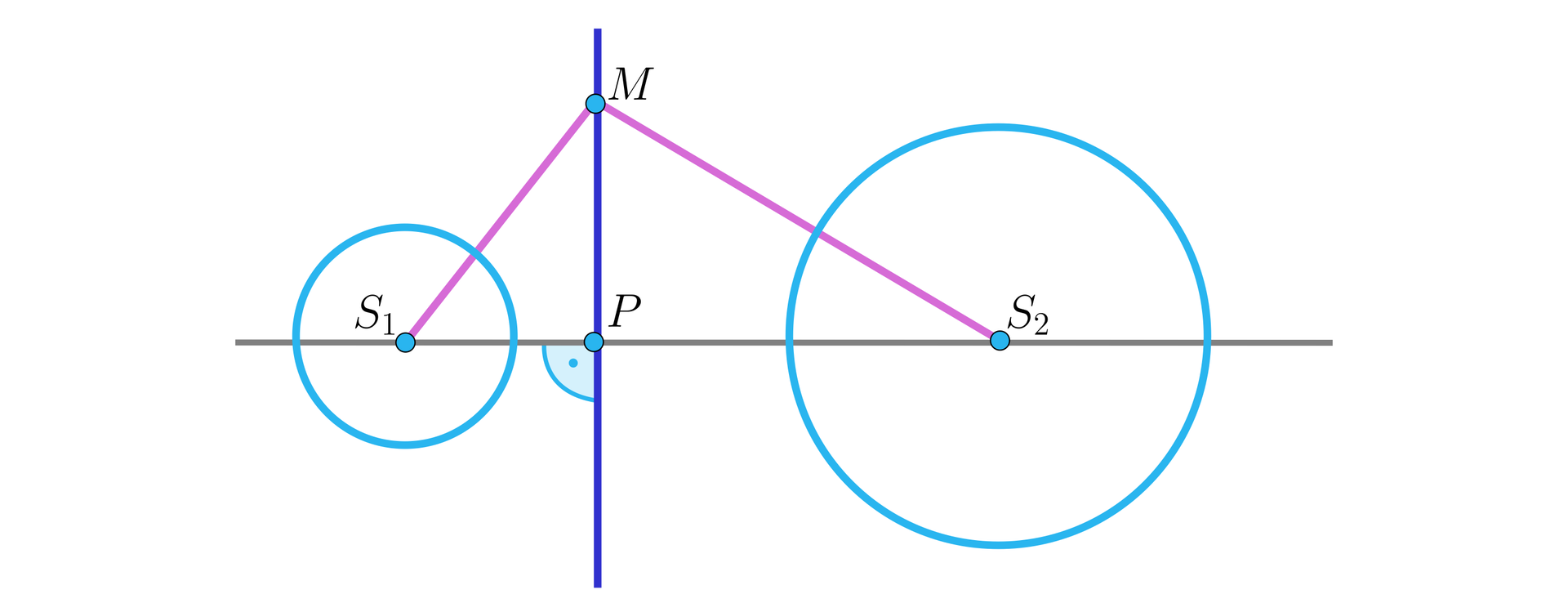
Dane są dwa okręgi: o środku $S_{1}$ i promieniu $r$ oraz o środku $S_{2}$ i promieniu $R$ takie, że odległość ich środków jest równa $D$ . Na prostej łączącej środki obu tych okręgów leży taki punkt $P$ , dla którego potęga względem obu okręgów jest równa. Wyznacz odległość $d$ punktu $P$ od środka $S_{1}$ .

Przyjmijmy oznaczenia, jak na rysunku.

R1EE3Mb5zP2tP

Na ilustracji przedstawiono dwa okręgi o środkach w punktach S1 i S2. Poprowadzono prostą przechodzącą przez środki okręgów, przez punkt Q leżący na okręgu pierwszym, oraz przez punkt R leżący na okręgu drugim. Pomiędzy okręgami, na środku prostej łączącej środki leży punkt P.

Wtedy: $|P S_{1}| = d$ , $|Q S_{1}| = r$ , $|R S_{2}| = R$ , $|S_{1} S_{2}| = D$ .

Zadaną równość potęg punktu $P$ względem obu okręgów możemy zapisać w postaci $(d + r) \cdot (d - r) = (D - d + R) \cdot (D - d - R)$ . Po rozwinięciu otrzymujemy $d^{2} - r^{2} = D^{2} - 2 d D + d^{2} - R^{2}$ . Stąd $d = \frac{D^{2} + r^{2} - R^{2}}{2 D}$ .

Ćwiczenie 4

Rozważmy dwa okręgi: o środkach w punktach $S_{1}$ i $S_{2}$ i promieniach odpowiednio $r$ i $R$ . Niech $P$ będzie punktem leżącym na prostej $S_{1} S_{2}$ , dla którego potęga względem obu okręgów jest taka sama. Wykaż, że dla każdego punktu leżącego na prostopadłej do prostej $S_{1} S_{2}$ i przechodzącej przez punkt $P$ , potęga względem obu okręgów jest równa

Przyjmijmy oznaczenia, jak na rysunku oraz $|P S_{1}| = a$ , $|P S_{2}| = b$ , $|M S_{1}| = c$ , $|M S_{2}| = d$ .

RW2026YUlinbB

Na ilustracji przedstawiono dwa okręgi, o środkach w punktach S1 i S2. Przez środki okręgów przechodzi prostą L, na której zaznaczono punkt P znajdujący się między okręgami. Zaznaczono punkt M, leżący na prostej prostopadłej do prostej L, przechodzący przez punkt P. Kolorem różowym zaznaczono odcinek MS1, oraz MS2.

Wtedy $c^{2} = a^{2} + {|M P|}^{2}$ oraz $d^{2} = b^{2} + {|M P|}^{2}$ . Z równości potęg punktu $P$ względem obu okręgów wynika, że $(a + r) (a - r) = (b + R) (b - R)$ , czyli $a^{2} - r^{2} = b^{2} - R^{2}$ .

Zauważmy, że potęgę punktu $M$ względem okręgu o środku $S_{1}$ możemy zapisać jako $(c + r) (c - r)$ . Wtedy
$(c + r) (c - r) = c^{2} - r^{2} = a^{2} + {|M P|}^{2} - r^{2} =$
$= a^{2} - r^{2} + {|M P|}^{2} = b^{2} - R^{2} + {|M P|}^{2} =$
$= d^{2} - R^{2} = (d + R) (d - R)$ .
Ale ostatni iloczyn jest potęgą punktu $M$ względem okręgu o środku $S_{2}$ . Wobec dowolności wyboru punktu $M$ otrzymujemy tezę.

Warto nadmienić, że prostą o tej własności nazywamy prostą potęgową lub osią potęgową dwóch okręgów.

Ćwiczenie 5

R1Qsbqd0THl2E

R1XDqyPlbHLEN

Ćwiczenie 6

R1XmMlCv5vFJ3

Ćwiczenie 7

Punkt $O$ jest środkiem okręgu, w którym $|P R| = 12$ , $|P N| = 9$ , $|P Q| = 15$ , jak na rysunku.

RzrlCPogxPhRK

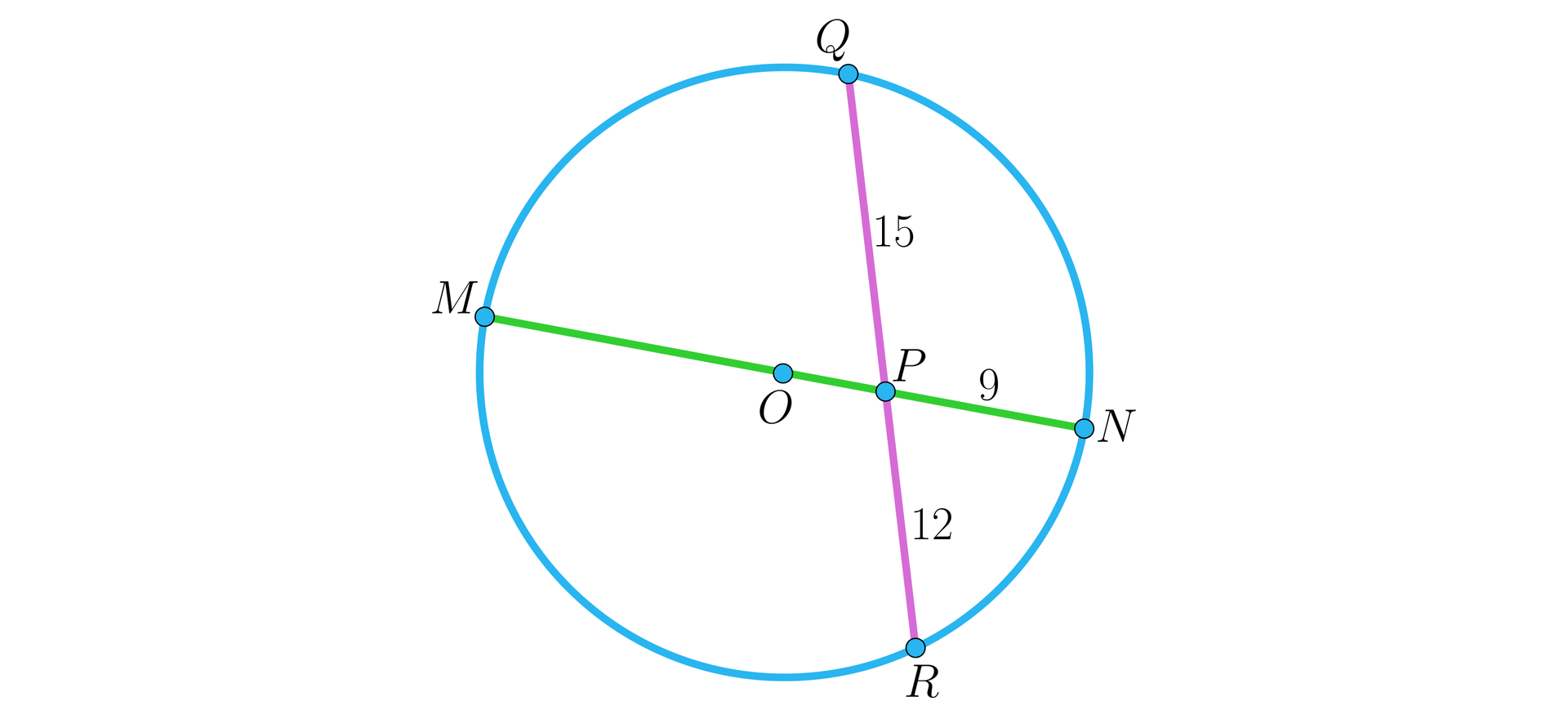
Na ilustracji przedstawiono okrąg o środku w punkcie O. Zaznaczono średnicę łączącą punkty M i N, oraz cięciwę łączącą punkty Q i R. Zaznaczono punkt P w miejscu przecięcia średnicy i cięciwy.

Promień tego okręgu jest równy

R1DgEPvhsBjJs

Ćwiczenie 8

Niech $P$ będzie punktem wspólnym cięciw $M N$ i $Q R$ danego okręgu, jak na rysunku

R1DlPVEfPhdiT

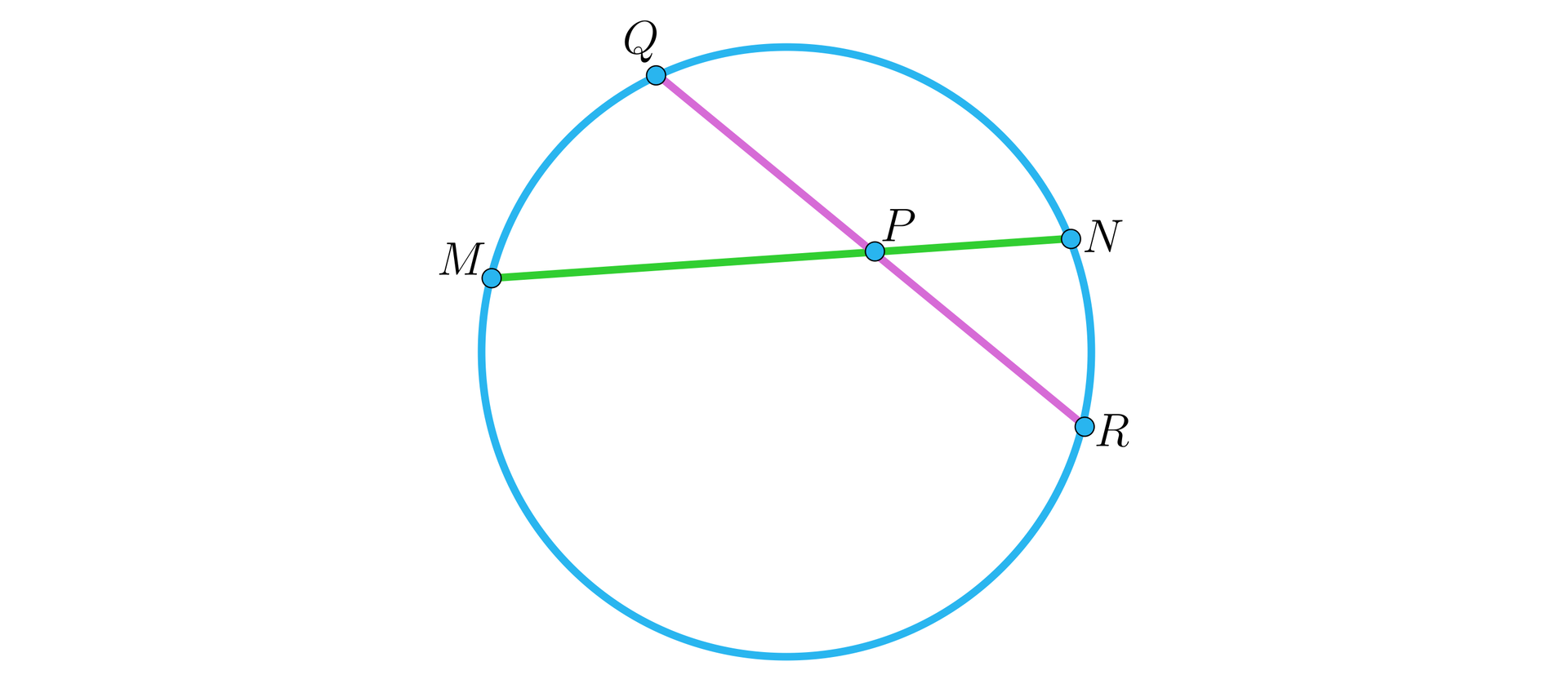
Na ilustracji przedstawiono okrąg, na którym zaznaczono dwie przecinające się cięciwy w punkcie P. Na okręgu zaznaczono cztery punkty. Cięciwa pierwsza łączy punkt Q z punktem R. Cięciwa druga łączy punkt M z punktem N.

Uzasadnij, że $|P M| \cdot |P N| = |P Q| \cdot |P R|$ .

Ułóż w kolejności etapy dowodu.

R4TvdcSlOhcVc

Animacja

Dla nauczyciela