Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
Ćwiczenie 2
Ćwiczenie 3
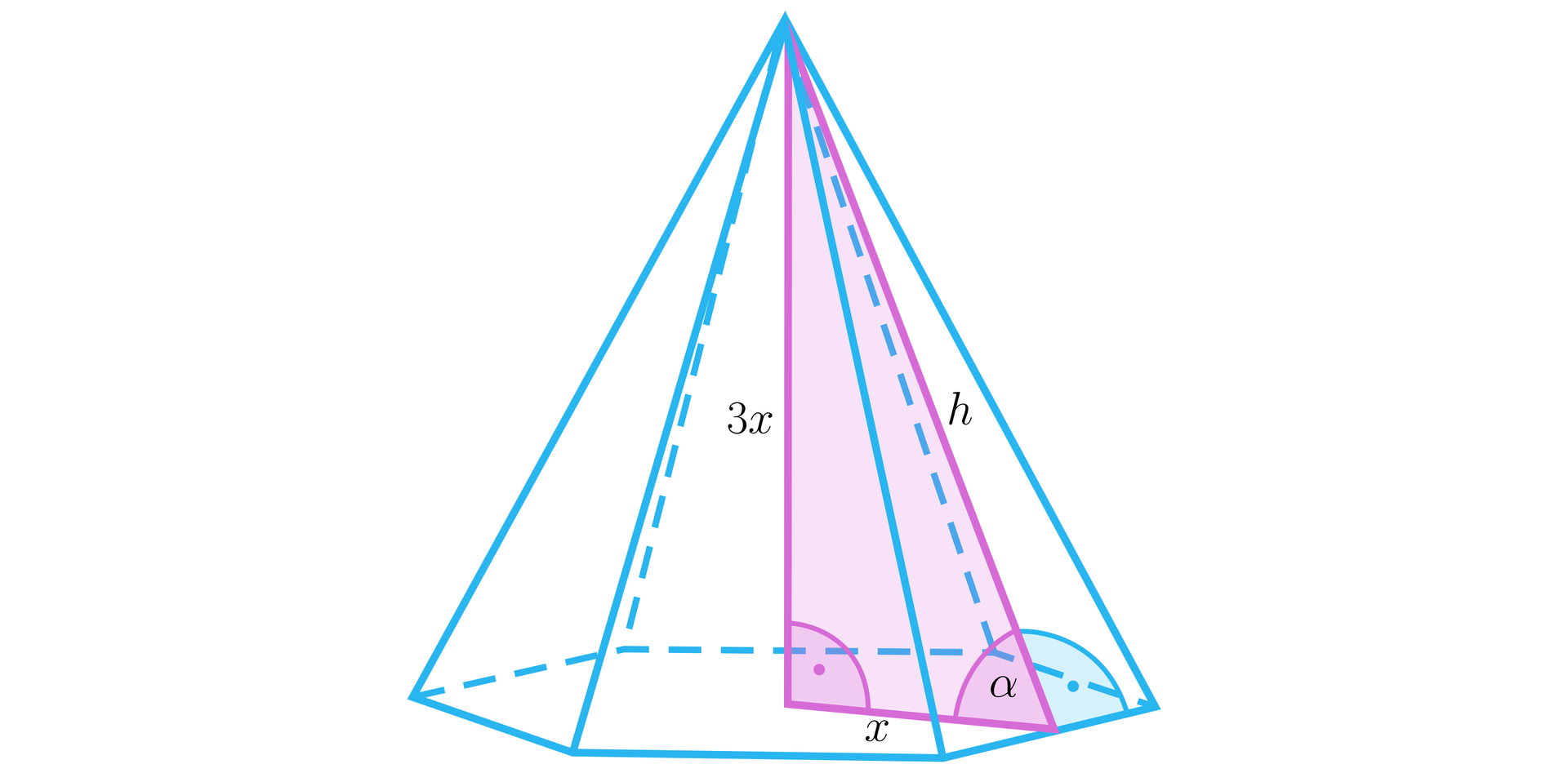
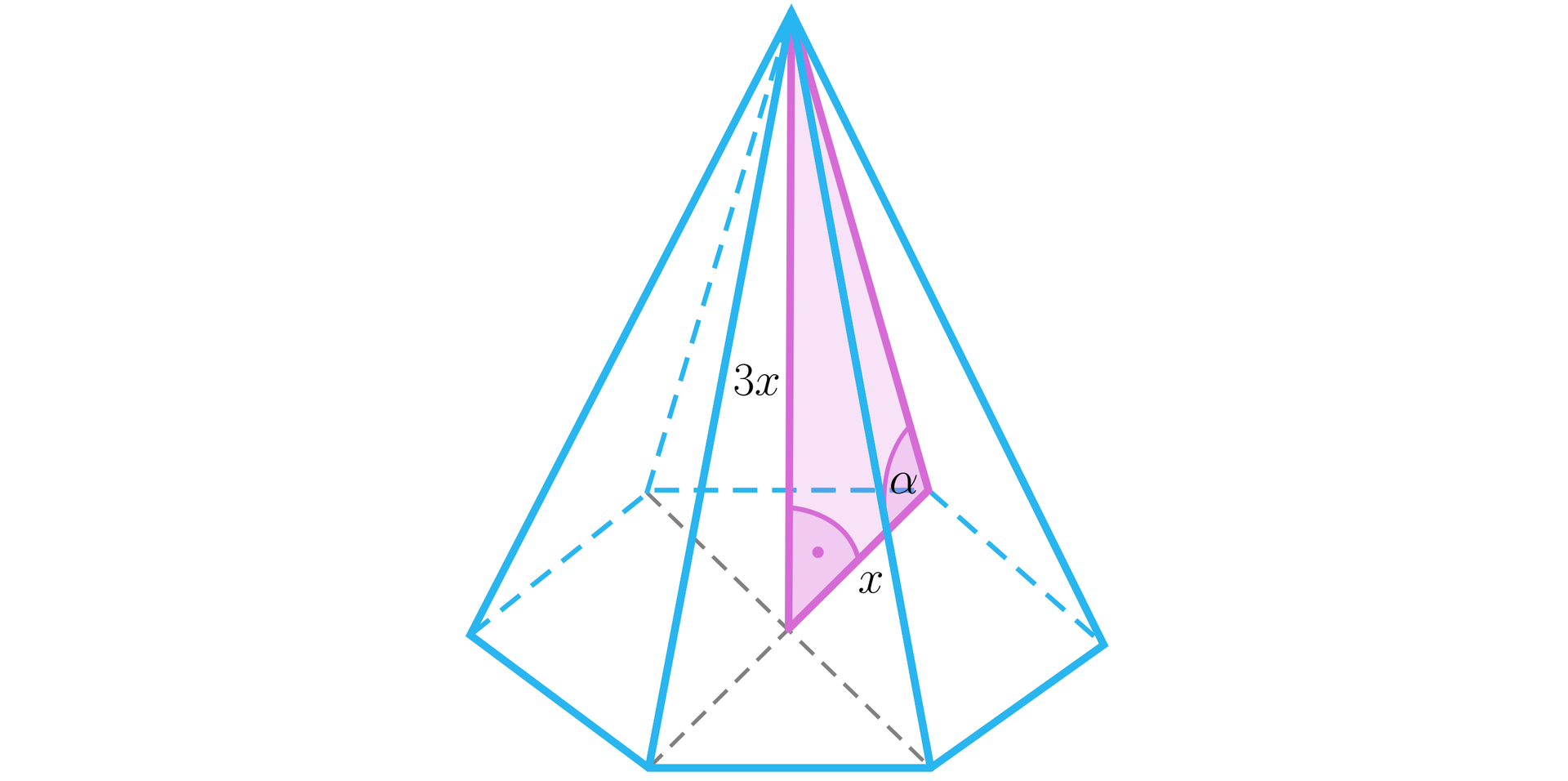
Krawędź boczna ostrosłupa prawidłowego sześciokątnego przedstawionego na rysunku ma miarę . Wysokość ostrosłupa ma długość .
Ćwiczenie 4
Oceń prawdziwość poniższych zdań. Przy każdym zdaniu w tabeli zaznacz „Prawda” albo „Fałsz”. . Dla przekrój będzie trójkątem równobocznym.. Możliwe odpowiedzi: Prawda, Fałsz. Dla przekrój będzie trójkątem rozwartokątnym.. Możliwe odpowiedzi: Prawda, Fałsz. Dla objętość ostrosłupa wynosi .. Możliwe odpowiedzi: Prawda, Fałsz
Ćwiczenie 5
- Objętość ostrosłupa wynosi 1. , 2. , 3. , 4. .
- Sinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy wynosi 1. , 2. , 3. , 4. .
Ćwiczenie 6
Ćwiczenie 7
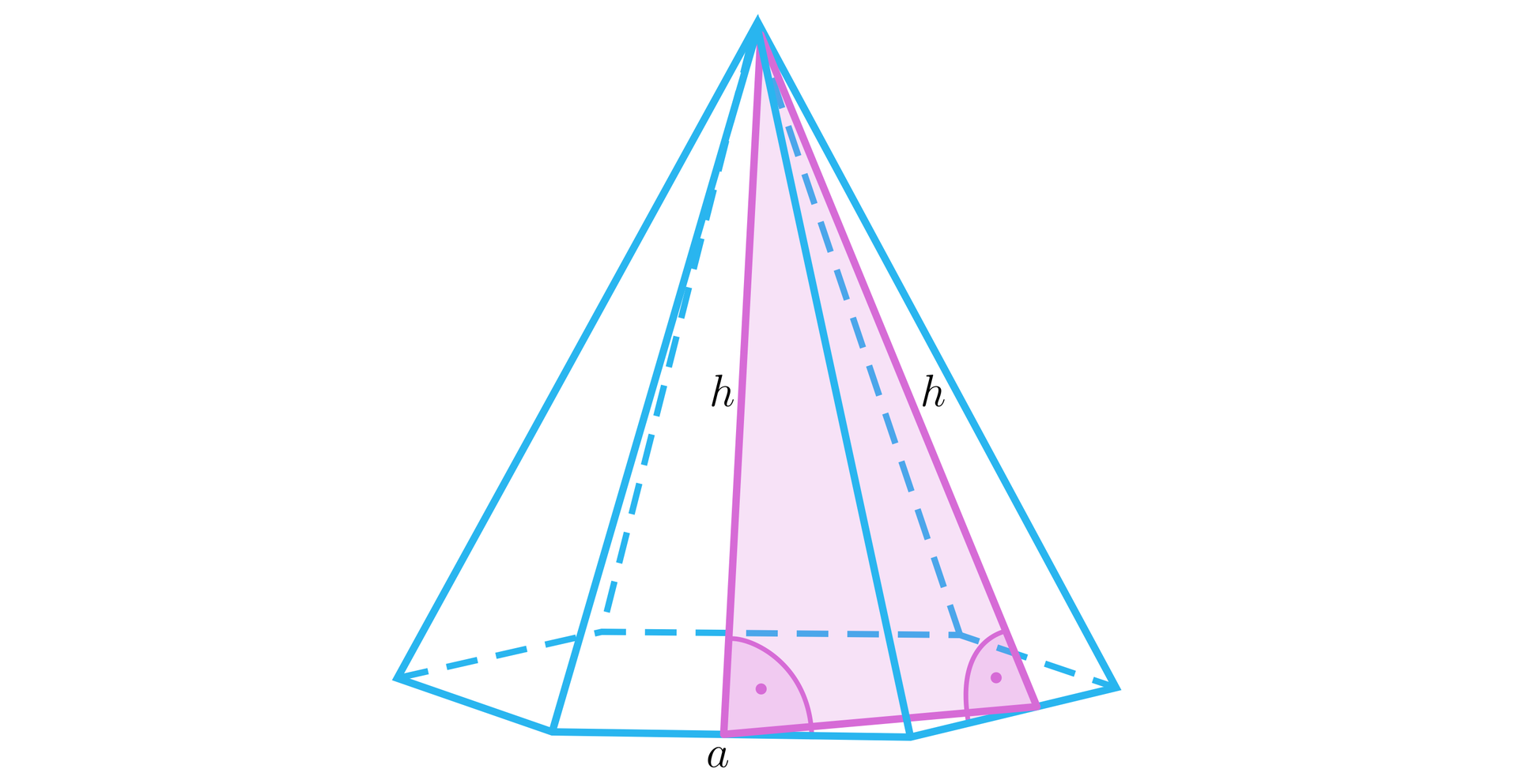
Tangens kąta nachylenia ściany bocznej ostrosłupa prawidłowego sześciokątnego do płaszczyzny podstawy wynosi . Wysokość ściany bocznej ma długość . Wykaż, że objętość ostrosłupa wynosi .
Ćwiczenie 8
Ostrosłup prawidłowy sześciokątny o krawędzi podstawy przecięto płaszczyzną przechodzącą przez wysokości dwóch sąsiednich ścian bocznych i wierzchołek ostrosłupa. Pole przekroju wynosi . Oblicz objętość ostrosłupa.