Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Przekątna zaznaczonego przekroju graniastosłupa prawidłowego czworokątnego z rysunku ma długość:

R12pVDA3flzOo

Na ilustracji przedstawiono graniastosłup prosty o podstawie kwadratu. Długości krawędzi podstawy wynosi 8, natomiast długość krawędzi bocznej wynosi dziesięć. Zaznaczono przekrój graniastosłupa, którego płaszczyzna jest prostokątem. Boki prostokąta stanowią krawędzie podstaw graniastosłupa, oraz przekątne przeciwległych ścian bocznych graniastosłupa.

RTxemIz5mnfrM

Ćwiczenie 2

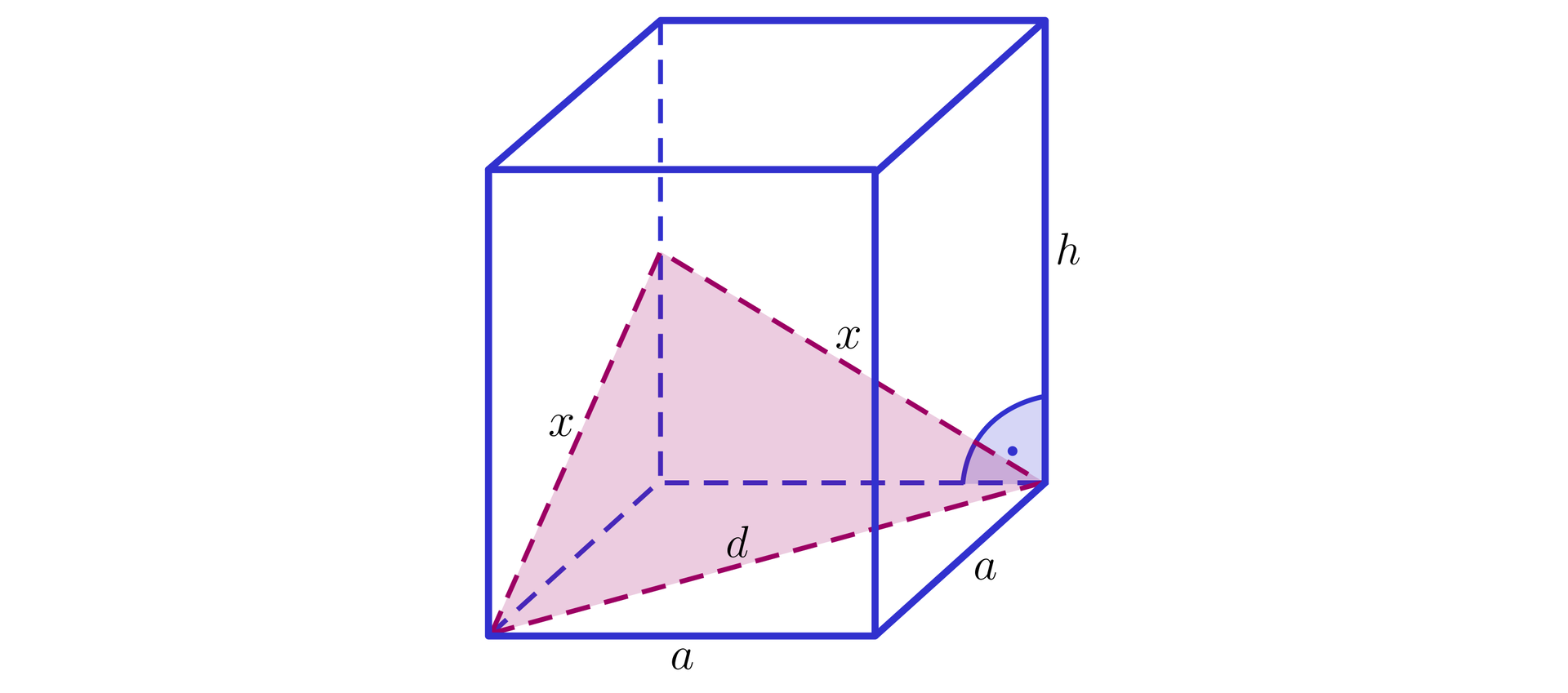
Na rysunku przedstawiono przekrój graniastosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i środek krawędzi bocznej.

R1Ko2U9io8WDi

Na ilustracji przedstawiono graniastosłup o podstawie kwadratu. Zaznaczono w nim przekrój, którego płaszczyznę stanowi trójkąt. Jedna z krawędzi trójkąta zawiera się w przekątnej podstawy graniastosłupa. Pozostałe dwie krawędzie zawierają się w sąsiadujących ścianach bocznych. Wierzchołek z którego wychodzą dwie krawędzie trójkąta znajduję się w połowie krawędzi bocznej graniastosłupa. Wszystkie krawędzie trójkąta mają długość 8.

R1H3PHVxfEpRQ

Ćwiczenie 3

RLTYLfgO2T3cw

R1aadNmic2GAU

Ćwiczenie 4

Na rysunku przedstawiono przekrój graniastosłupa prawidłowego czworokątnego pewną płaszczyzną.

R5sefCMrtEQKw

Ilustracja przedstawia graniastosłup prosty o podstawie kwadratu. Krawędzie podstawy oznaczono literą a, natomiast krawędź boczną literą h. Przekątna ściany bocznej jest nachylona do krawędzi bocznej h, pod kątem sześćdziesięciu stopni. Zaznaczono przekrój graniastosłupa, którego płaszczyznę stanowi trójkąt ograniczony dwoma przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka oraz przekątną podstawy.

R10wMPXxxOs7b

Wstaw w tekst odpowiednie zwroty lub wartości. Narysowany przekrój graniastosłupa prawidłowego czworokątnego jest trójkątem 1.

h \sqrt{6}

, 2.

\frac{2 a \sqrt{3}}{3}

, 3.

\frac{4 a \sqrt{3} + 3 a \sqrt{2}}{3}

, 4.

2 a \sqrt{3}

, 5. równoramiennym, 6.

h \sqrt{3}

, 7. różnoramiennym, 8. równobocznym, 9.

2 a

, 10.

\frac{3 a \sqrt{3} + 4 a \sqrt{2}}{3}

.
Długość ramienia trójkąta będącego danym przekrojem jest równa 1.

h \sqrt{6}

, 2.

\frac{2 a \sqrt{3}}{3}

, 3.

\frac{4 a \sqrt{3} + 3 a \sqrt{2}}{3}

, 4.

2 a \sqrt{3}

, 5. równoramiennym, 6.

h \sqrt{3}

, 7. różnoramiennym, 8. równobocznym, 9.

2 a

, 10.

\frac{3 a \sqrt{3} + 4 a \sqrt{2}}{3}

.
Podstawa trójkąta będącego przekrojem ma długość 1.

h \sqrt{6}

, 2.

\frac{2 a \sqrt{3}}{3}

, 3.

\frac{4 a \sqrt{3} + 3 a \sqrt{2}}{3}

, 4.

2 a \sqrt{3}

, 5. równoramiennym, 6.

h \sqrt{3}

, 7. różnoramiennym, 8. równobocznym, 9.

2 a

, 10.

\frac{3 a \sqrt{3} + 4 a \sqrt{2}}{3}

.
Obwód trójkąta będącego przekrojem graniastosłupa prawidłowego czworokątnego jest równy 1.

h \sqrt{6}

, 2.

\frac{2 a \sqrt{3}}{3}

, 3.

\frac{4 a \sqrt{3} + 3 a \sqrt{2}}{3}

, 4.

2 a \sqrt{3}

, 5. równoramiennym, 6.

h \sqrt{3}

, 7. różnoramiennym, 8. równobocznym, 9.

2 a

, 10.

\frac{3 a \sqrt{3} + 4 a \sqrt{2}}{3}

RGuYZHcputEY42

Ćwiczenie 5

Ćwiczenie 6

Oblicz obwód przekroju graniastosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przez przekątną podstawy i środek krawędzi bocznej, jeżeli pole powierzchni podstawy graniastosłupa wynosi $28$ , a krawędź boczna ma długość $8$ .

Narysujmy graniastosłup prawidłowy czworokątny, omawiany przekrój i wprowadźmy oznaczenia, jak na poniższym rysunku.

Ro1cgno99I7x1

Na ilustracji przedstawiono graniastosłup prosty o podstawie kwadratu. Długości krawędzi podstawy oznaczono literą a, natomiast długość krawędzi bocznej oznaczono h. Zaznaczono przekrój graniastosłupa, którego płaszczyznę stanowi trójkąt równoramienny. Podstawa trójkąta jest przekątną podstawy graniastosłupa, natomiast ramiona są przeciwprostokątnymi trójkątów prostokątnych o przyprostokątnych a i jedna druga h. Długości ramion trójkąta oznaczono literą x, natomiast długość podstawy literą d.

Z treści zadania wiadomo, że pole podstawy graniastosłupa wynosi $28$ oraz $h = 8$ .

Zatem $a^{2} = 28$ , więc $a = 2 \sqrt{7}$ .

Otrzymany przekrój jest trójkątem równoramiennym o podstawie długości $d$ i ramionach długości $x$ .

Zauważmy, że $d = a \sqrt{2} = 2 \sqrt{7} \cdot \sqrt{2} = 2 \sqrt{14}$ .

Do wyznaczenia wartości $x$ rozwiązujemy równanie, korzystając z twierdzenia Pitagorasa:

$x^{2} = a^{2} + {(\frac{1}{2} h)}^{2}$

$x^{2} = {(2 \sqrt{7})}^{2} + 4^{2}$

$x^{2} = 28 + 16 = 44$

$x = 2 \sqrt{11}$

Zatem obwód trójkąta, który jest przekrojem graniastosłupa z rysunku wynosi:

$L = 2 \sqrt{14} + 2 \cdot 2 \sqrt{11} = 2 \cdot (\sqrt{14} + 2 \sqrt{11})$ .

Ćwiczenie 7

Jeżeli przekrojem graniastosłupa prawidłowego czworokątnego z rysunku jest trójkąt równoboczny, to:

RNDjS2ZNMH3jf

Ilustracja przedstawia graniastosłup o podstawie kwadratu. Krawędzie podstawy oznaczono literą a, natomiast krawędź boczną literą h. Zaznaczono przekrój graniastosłupa, którego płaszczyznę stanowi trójkąt ograniczony dwoma przekątnymi ścian bocznych wychodzącymi z jednego wierzchołka oraz przekątną podstawy.

RJlhzp33vuZL1

Ćwiczenie 8

Na rysunku przedstawiono przekrój graniastosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez środki dwóch krawędzi bocznych graniastosłupa.

R3AHrq2qJBjDa

Na ilustracji przedstawiono graniastosłup prosty o podstawie kwadratu. Długości krawędzi podstawy wynoszą 42, natomiast długość krawędzi bocznej jest równa cztery. W graniastosłupie zaznaczono prostokąt stanowiący jego płaszczyznę przekroju. Długości boków prostokąta wynoszą 42, y oraz przekątną oznaczono literą z. Jedna z krawędzi prostokąta pokrywa się z krawędzią podstawy graniastosłupa, a przeciwległa do niej krawędź znajduję się w ścianie bocznej graniastosłupa. Na tej samej ścianie bocznej graniastosłupa jego krawędź podstawy dolnej i krawędź prostokąta są od siebie oddalone o x. Pozostałe krawędzie prostokąta znajdują się w sąsiadujących ścianach bocznych graniastosłupa.

RRNTIILW7d38S

Aplet

Dla nauczyciela