Sprawdź się
Poniższe drzewo opisuje przebieg pewnego doświadczenia losowego polegającego na kolejnym losowaniu trzech kul z urny.

Poniższe drzewo opisuje przebieg pewnego doświadczenia losowego polegającego na kolejnym losowaniu trzech kul.
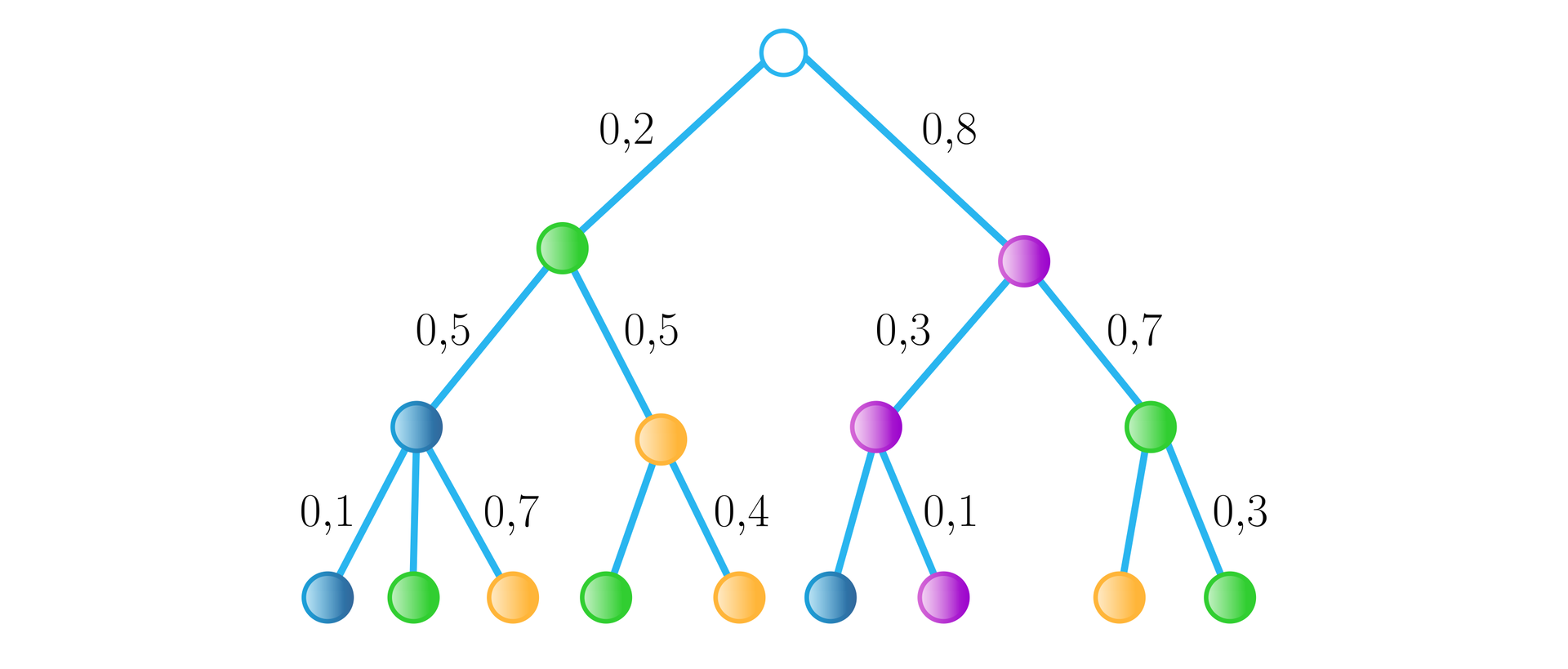
Drzewo opisuje przebieg pewnego doświadczenia losowego polegającego na kolejnym losowaniu trzech kul.
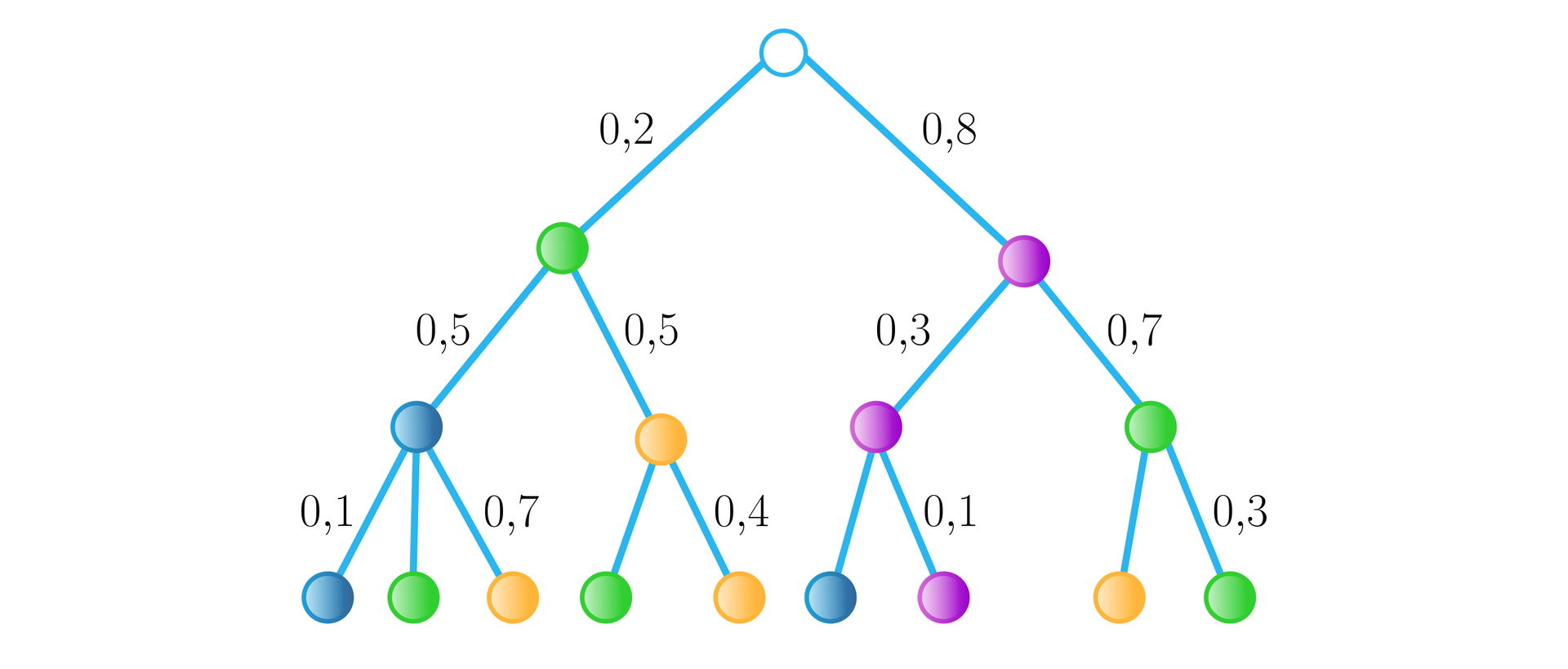
Niech oznacza zdarzenie: za trzecim razem wylosowano kulę pomarańczową.
W koszyku znajdują się wiśnie i czereśnie . Na drzewie probabilistycznym zaznaczono wyniki losowania z koszyka dwóch owoców.
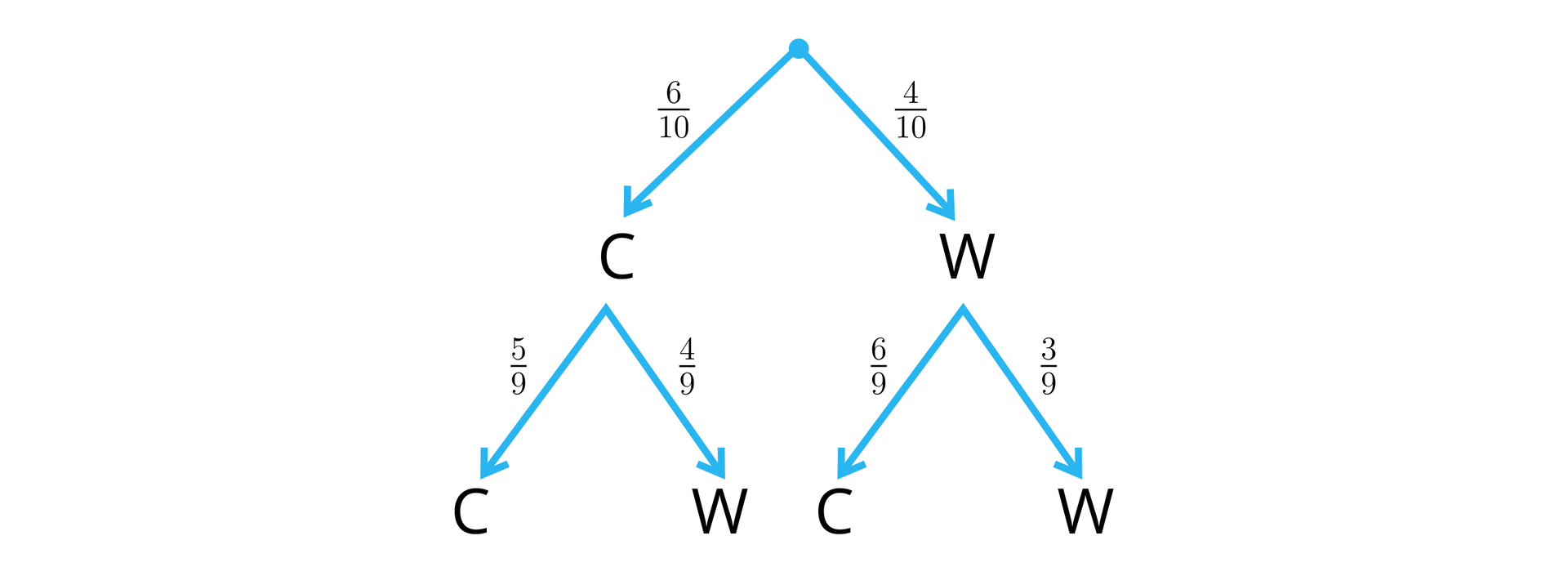
Połącz w pary opis zdarzenia i prawdopodobieństwo tego zdarzenia. Żadna z wylosowanych liczb nie jest pierwsza. Możliwe odpowiedzi: 1. , 2. , 3. , 4. Obydwie wylosowane liczby są pierwsze. Możliwe odpowiedzi: 1. , 2. , 3. , 4. Przynajmniej jedna z wylosowanych liczb jest pierwsza. Możliwe odpowiedzi: 1. , 2. , 3. , 4. Jedna z wylosowanych liczb jest pierwsza, a druga złożona. Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Rzucamy kostką do gry i symetryczną monetą. Oznaczmy:
– wypadnie parzysta liczb oczek,
– wypadnie nieparzysta liczba oczek,
– wypadnie orzeł,
– wypadnie reszka.

- Prawdopodobieństwo wyrzucenia dokładnie jednego orła jest równe Tu uzupełnij.
- Prawdopodobieństwo wyrzucenia za drugim razem nieparzystej liczby oczek jest równe Tu uzupełnij.
- Prawdopodobieństwo wyrzucenia dwóch reszek jest równe Tu uzupełnij.
Strzelec strzela do tarczy tylko trzy razy. Prawdopodobieństwo trafienia do tarczy za pierwszym razem jest równe . Po każdym strzale zmniejsza się o . Sporządź odpowiednie drzewo i oblicz prawdopodobieństwo tego, że przy trzykrotnym strzale strzelec trafi co najmniej raz.
W urnie znajduje się kul (), w tym zielonych. Z urny losujemy kolejno bez zwracania dwie kule.
Znajdź liczbę , dla której prawdopodobieństwo wylosowania dwóch kul zielonych jest większe od .