Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Długości dwóch boków i miara kąta między tymi bokami zostały zaznaczone na rysunku.

RByI96MleFfk0

Ilustracja przedstawia trójkąt o bokach o długości 11, a 17; między bokami o długości 11 i 17 zaznaczono kąt o mierze 60 stopni.

RY9M5s9YliPN1

Zaznacz poprawną odpowiedź. Długość $a$ trzeciego boku tego trójkąta jest liczbą należącą do przedziału:

$(12, 13)$
$(13, 14)$
$(14, 15)$
$(15, 16)$

Ćwiczenie 2

W trójkącie ostrokątnym $A B C$ (oznaczenia standardowe jak na rysunku)

RB43authLPbHj

Ilustracja przedstawia trójkąt ostrokątny ABC o kątach wewnętrznych przy wierzchołku A kąt alfa, przy wierzchołku B kąt beta, przy wierzchołku C kąt gamma. Odcinek AB ma miarę c, odcinek BC ma miarę a, odcinek AC ma miarę b.

boki mają długości: $a = 6$ , $b = 5$ , $c = 4$ .

ReuhhJoeZLNxI

Uzupełnij, przeciągając odpowiedni przedział, tak, żeby otrzymać zdania prawdziwe.

$"⟨"20 °, 30 °")"$ , $"⟨"70 °, 80 °")"$ , $"⟨"40 °, 50 °")"$ , $"⟨"30 °, 40 °")"$ , $"⟨"60 °, 70 °")"$ , $"⟨"50 °, 60 °")"$ , $"⟨"80 °, 90 °")"$ , $"⟨"10 °, 20 °")"$

$α \in$
$β \in$
$γ \in$

RTghtSexbMIjZ1

Ćwiczenie 3

Zaznacz poprawną odpowiedź. Liczby całkowite ustawione w kolejności rosnącej: $7$ , $11$ , $x$ są długościami boków trójkąta ostrokątnego. Wynika stąd, że:

taka trójka liczb nie istnieje.
jest tylko jedna taka trójka liczb.
są dokładnie dwie takie trójki liczb.
są dokładnie trzy takie trójki liczb.
takich trójek liczb jest nieskończenie wiele.

Ćwiczenie 4

W trójkącie $A B C$ (oznaczenia standardowe jak na rysunku) prawdziwe są równości $a^{2} = b^{2} + c^{2} - 2 b c \sin α$ , $b^{2} = a^{2} + c^{2} - 2 a c \sin β$ .

R1SJdljrUB1aM

R1cI4QVSz6b71

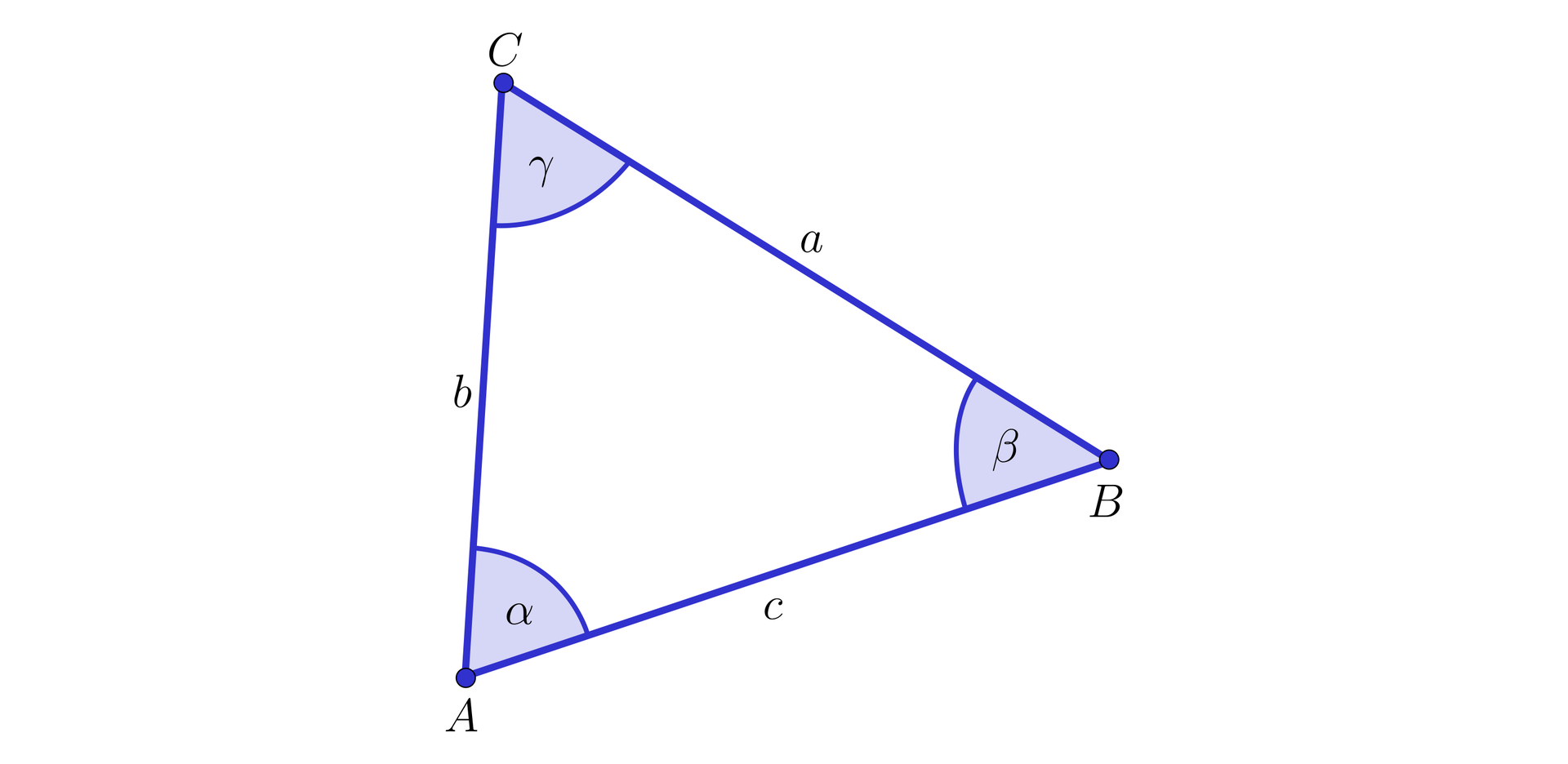
Wskaż wszystkie zdania prawdziwe.

Trójkąt $A B C$ jest równoramienny.
Trójkąt $A B C$ jest równoboczny.
Trójkąt $A B C$ jest prostokątny.
Jeden z kątów trójkąta $A B C$ jest dwa razy większy od drugiego z kątów tego trójkąta.
Trójkąt $A B C$ jest rozwartokątny.

RCtUdHfmtdBSm2

Ćwiczenie 5

Zaznacz fałszywą odpowiedź. W trójkącie $A B C$ dane są: $"|"A B"|" = 8$ , $"|"B C"|" = 7$ i $"|"∢ B A C"|" = 60 °$ . Wynika stąd, że:

długość boku $A C$ tego trójkąta może być równa $5$ .
długość boku $A C$ tego trójkąta jest liczbą pierwszą.
długość boku $A C$ tego trójkąta może być liczbą niewymierną.

Ćwiczenie 6

Udowodnij, że jeśli w trójkącie stosunek długości dwóch boków jest równy podwojonemu cosinusowi kąta między tymi bokami, to ten trójkąt jest równoramienny.

Przyjmijmy standardowe oznaczenia w trójkącie i załóżmy, że $\frac{b}{c} = 2 \cos α$ .

Z twierdzenia cosinusów otrzymujemy $a^{2} = b^{2} + c^{2} - 2 \cdot b c \cos α$ .

Stąd i z założenia wynika zatem równość $a^{2} = b^{2} + c^{2} - 2 \cdot b c \cdot \frac{b}{2 c}$ .

Przekształcając tę równość mamy kolejno:

$a^{2} = b^{2} + c^{2} - b^{2}$ , $a^{2} = c^{2}$ , co oznacza, że $a = c$ , gdyż $a$ i $c$ to liczby dodatnie.

To kończy dowód.

Ćwiczenie 7

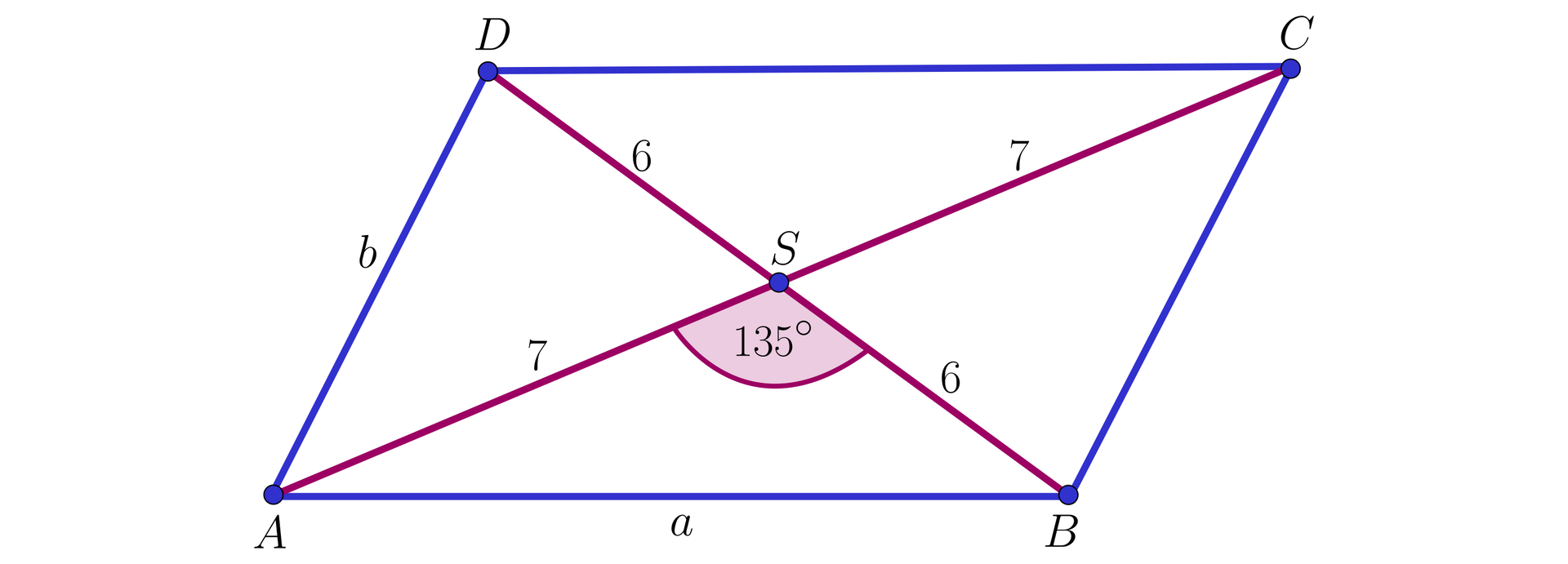
Przekątne równoległoboku przecinają się pod kątem $135 °$ a ich długości są równe $12$ i $14$ . Oblicz długości boków tego równoległoboku.

Przyjmijmy oznaczenia jak na rysunku.

RXp8bWEhd2s0h

Ilustracja przedstawia równoległobok ABCD o bokach długości a i b. Przekątne równoległoboku o długości 12 i 14 przecinają się w punkcie S i pod kątem 135 stopni.

Punkt $S$ przecięcia przekątnych $A C$ i $B D$ równoległoboku jest środkiem każdej z tych przekątnych, więc $|A S| = |C S| = 7$ i $|B S| = |D S| = 6$ .

Kąty $A S B$ i $B S C$ są przyległe, więc

$|∢ B S C| = 180 ° - |∢ A S B| = 180 ° - 135 ° = 45 °$ .

Z twierdzenia cosinusów dla trójkąta $A B S$ i trójkąta $B C S$ otrzymujemy

$a^{2} = 7^{2} + 6^{2} - 2 \cdot 7 \cdot 6 \cdot \cos 135 °$ oraz $b^{2} = 7^{2} + 6^{2} - 2 \cdot 7 \cdot 6 \cdot \cos 45 °$ .

Ponieważ $\cos 135 ° = \cos (180 ° - 45 °) = - \cos 45 ° = - \frac{\sqrt{2}}{2}$ , więc

$a^{2} = 49 + 36 - 2 \cdot 42 \cdot (- \frac{\sqrt{2}}{2})$ oraz $b^{2} = 49 + 36 - 2 \cdot 42 \cdot \frac{\sqrt{2}}{2}$ ,

$a^{2} = 85 + 42 \sqrt{2}$ oraz $b^{2} = 85 - 42 \sqrt{2}$ .

Stąd $a = \sqrt{85 + 42 \sqrt{2}}$ oraz $b = \sqrt{85 - 42 \sqrt{2}}$ .

Ćwiczenie 8

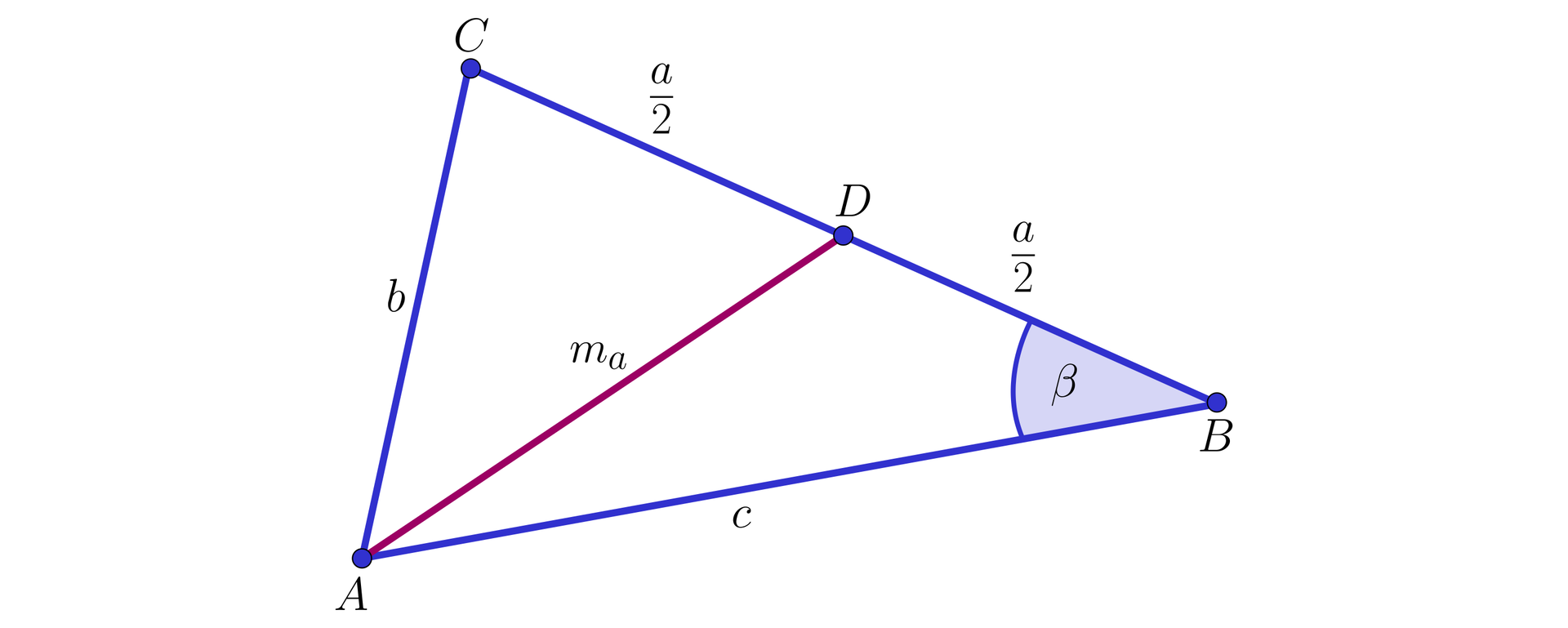
Wykaż, że długość $m_{a}$ środkowej $A D$ trójkąta $A B C$ jest równa $m_{a} = \frac{1}{2} \sqrt{2 b^{2} + 2 c^{2} - a^{2}}$ , gdzie $a = |B C|$ , $b = |A C|$ , $c = |A B|$ .

Przyjmijmy oznaczenia jak na rysunku.

R1WLEycf70kpj

Ilustracja przedstawia trójkąt ABC o kącie przy wierzchołku B równym beta. Odcinek AB ma miarę c, odcinek BC ma miarę a, odcinek AC ma miarę b. Z wierzchołka A poprowadzono prostą m indeks dolny a koniec indeksu na odcinek BC tworząc punkt D dzielący odcinek BC na dwie równe części.

Z twierdzenia cosinusów zastosowanego dla kąta $β$ w trójkątach $A B C$ i $A B D$ otrzymujmy $b^{2} = a^{2} + c^{2} - 2 a c \cos β$ oraz $m_{a}^{2} = {(\frac{1}{2} a)}^{2} + c^{2} - 2 \cdot \frac{1}{2} a c \cos β$ .

Z pierwszej z tych równości możemy wyznaczyć $a c \cos β = \frac{a^{2} + c^{2} - b^{2}}{2}$ (lub $\cos β$ ).

Stąd i z drugiej równości otrzymujemy $m_{a}^{2} = {(\frac{1}{2} a)}^{2} + c^{2} - \frac{a^{2} + c^{2} - b^{2}}{2}$ , czyli

$m_{a}^{2} = \frac{1}{4} a^{2} + c^{2} - \frac{1}{2} a^{2} - \frac{1}{2} c^{2} + \frac{1}{2} b^{2} = \frac{1}{2} b^{2} + \frac{1}{2} c^{2} - \frac{1}{4} a^{2} = \frac{1}{4} (2 b^{2} + 2 c^{2} - a^{2})$ , skąd $m_{a} = \frac{1}{2} \sqrt{2 b^{2} + 2 c^{2} - a^{2}}$ .

To kończy dowód.

Animacja

Dla nauczyciela