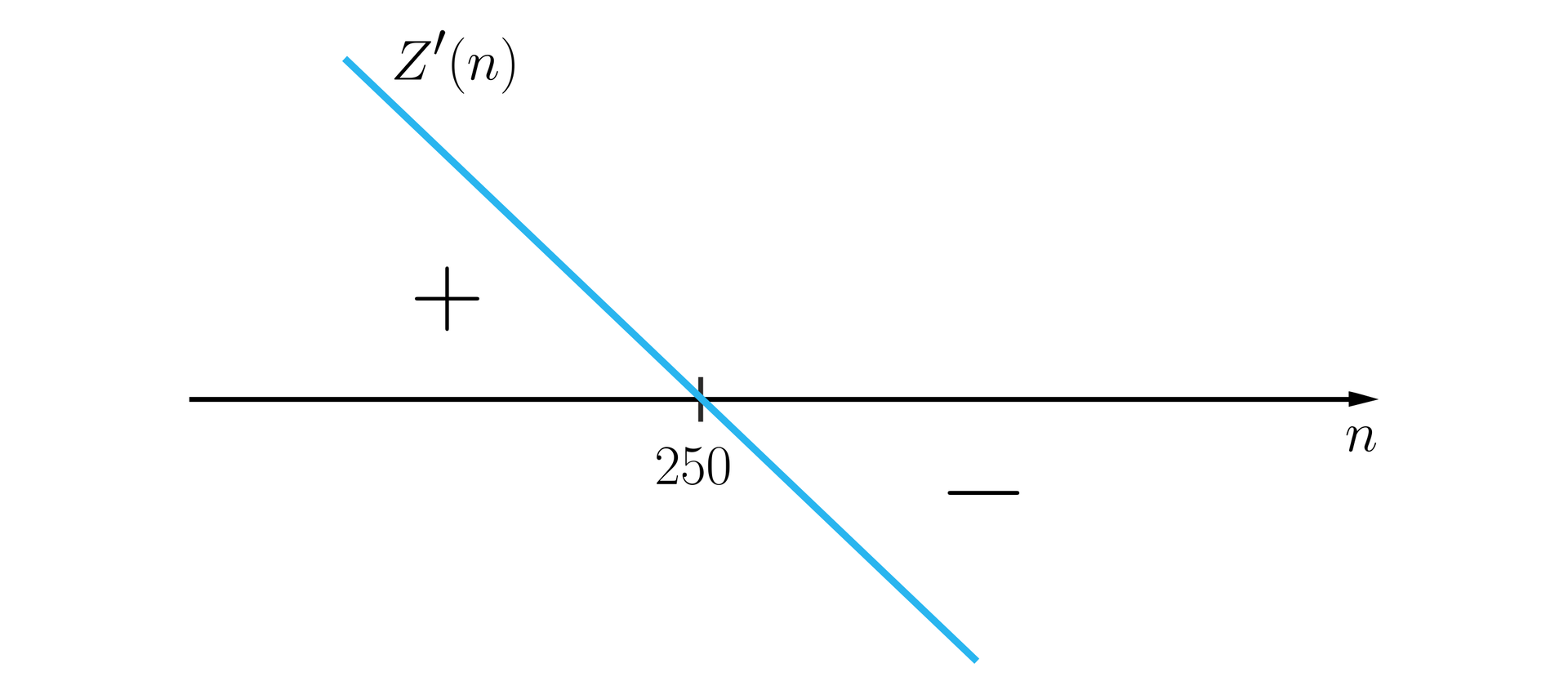Sprawdź się
1. , 2. , 3. , 4. , 5. , 6.
Przekątna przekroju osiowego puszki farby w kształcie walca ma długość . Wiedząc, że objętość jest największa z możliwych wyznacz promień oraz wysokość tej puszki farby.
, , , , ,
............ ,
............ .
Z balkonu podrzucono piłkę, która po sekundach spadła na ziemię. Wysokość (w metrach) na jakiej znajdowała się piłka nad ziemią po upływie sekund od podrzucenia opisuje funkcja , gdzie . Oblicz po jakim czasie od momentu podrzucenia piłka osiągnęła największą wysokość. Zaznacz poprawną odpowiedź.
- po połowie sekundy
- po jednej sekundzie
- po trzech sekundach
- po jednej czwartej sekundy
Pan Kowalski zajmuje się wynajmem sprzętu narciarskiego, ma do dyspozycji kompletów. Wszystkie komplety sprzętu są wykorzystane wówczas gdy cena jednego kompletu wynosi . Pewnego razu zaobserwował, że podwyżka kosztów wynajmu o każde zmniejsza liczbę wynajmowanych kompletów o . Jaki koszt wynajmu powinien ustalić Pan Kowalski, aby jego zysk był największy? Wyznacz ten zysk.
Koszt wynajmu ............ .
Zysk ............ .
Torebki "piramidki" z herbatą mają kształt ostrosłupa prawidłowego trójkątnego, w których krawędź boczna wynosi . Wiedząc, że objętość jest maksymalna, zaznacz prawidłowe odpowiedzi. Przyjmij – długość podstawy.
| Pytanie | Odpowiedź 1 | Odpowiedź 2 |
| Dziedzina | □ | □ |
| □ | □ | |
| □ | □ |
Działka w kształcie prostokąta o polu ma być otoczona chodnikiem. Jego szerokości po przeciwległych stronach trawnika są takie same i wynoszą i (zobacz rysunek).
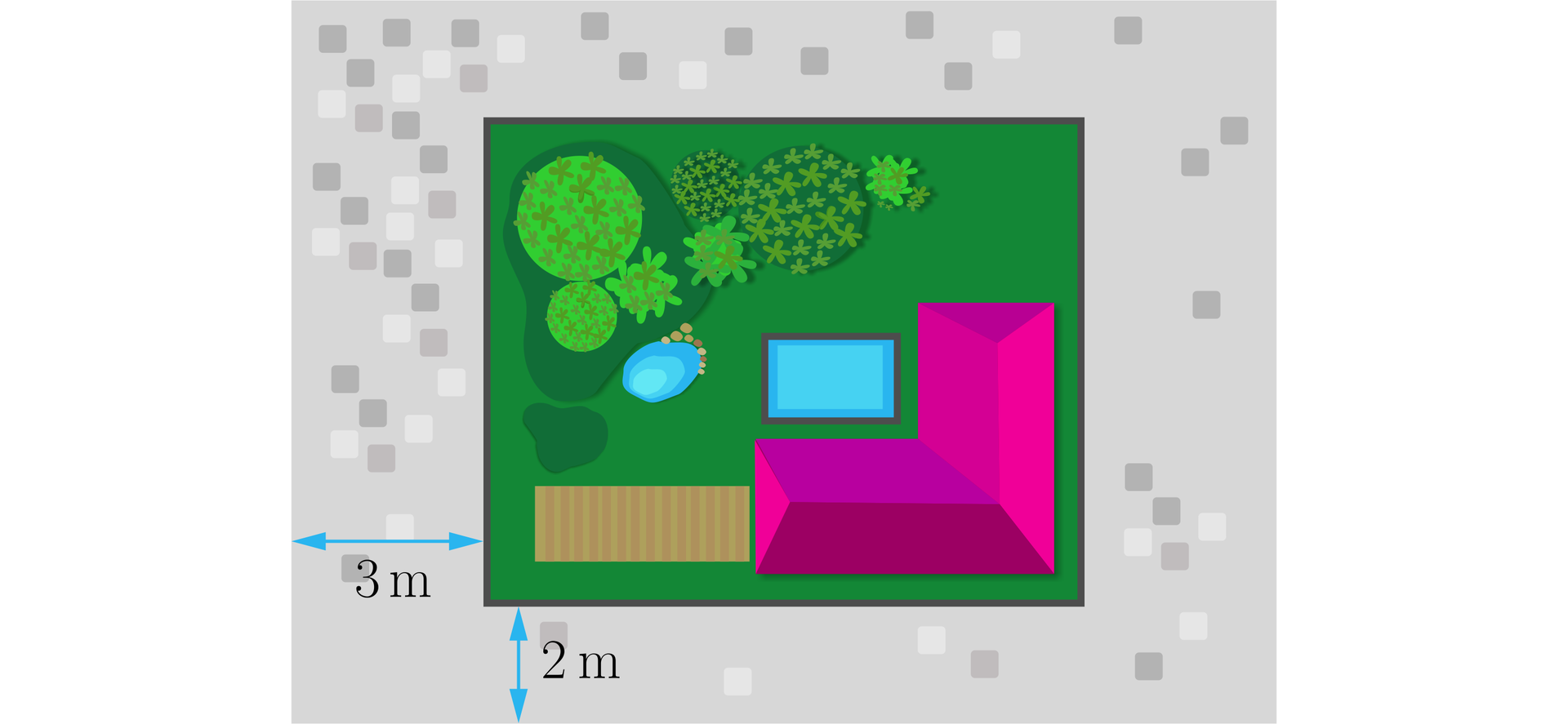
Wyznacz wymiary działki, aby chodnik zajmował najmniejszą powierzchnię. Wskaż poprawną odpowiedź.
Rolnik hoduje sztuk trzody chlewnej. Ze sprzedaży trzody chlewnej osiąga średni dzienny dochód wynoszący . Oszacowano, że gdy zwiększy się liczbę hodowanych świń, to dochód jaki przynosi średnio dziennie jedna trzoda chlewna, spadnie o promil wraz z każdą dodatkowo zakupioną sztuką. Oblicz ile sztuk trzody chlewnej powinien hodować rolnik, aby osiągnąć możliwie największy dochód.
Z drutu o długości wykonano szkielet akwarium, którego stosunek długości podstawy do szerokości wynosi . Wiedząc, że objętość jest największa, uzupełnij tabelę. Przyjmij – dłuższa krawędź podstawy.
MAX, BRAK, , , , , , , , , , , , , , ,
Świeczka w kształcie stożka ma objętość . Wyznacz promień i wysokość tej świeczki, wiedząc, że pole powierzchni całkowitej przyjmuje najmniejszą wartość.