Sprawdź się
Jeżeli , to:
- .
Zapoznaj się z rysunkiem, a następnie na jego podstawie wykonaj ćwiczenie.
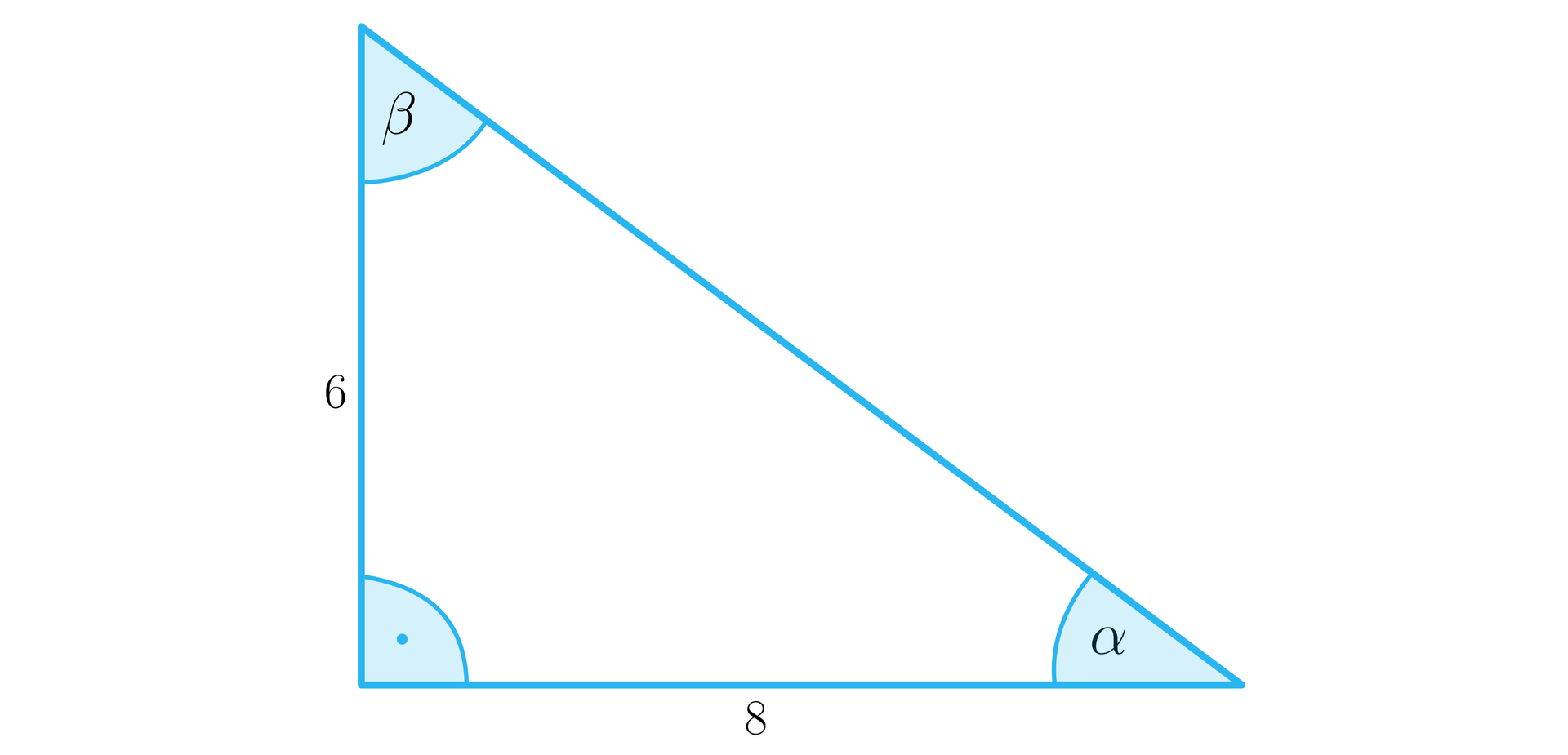
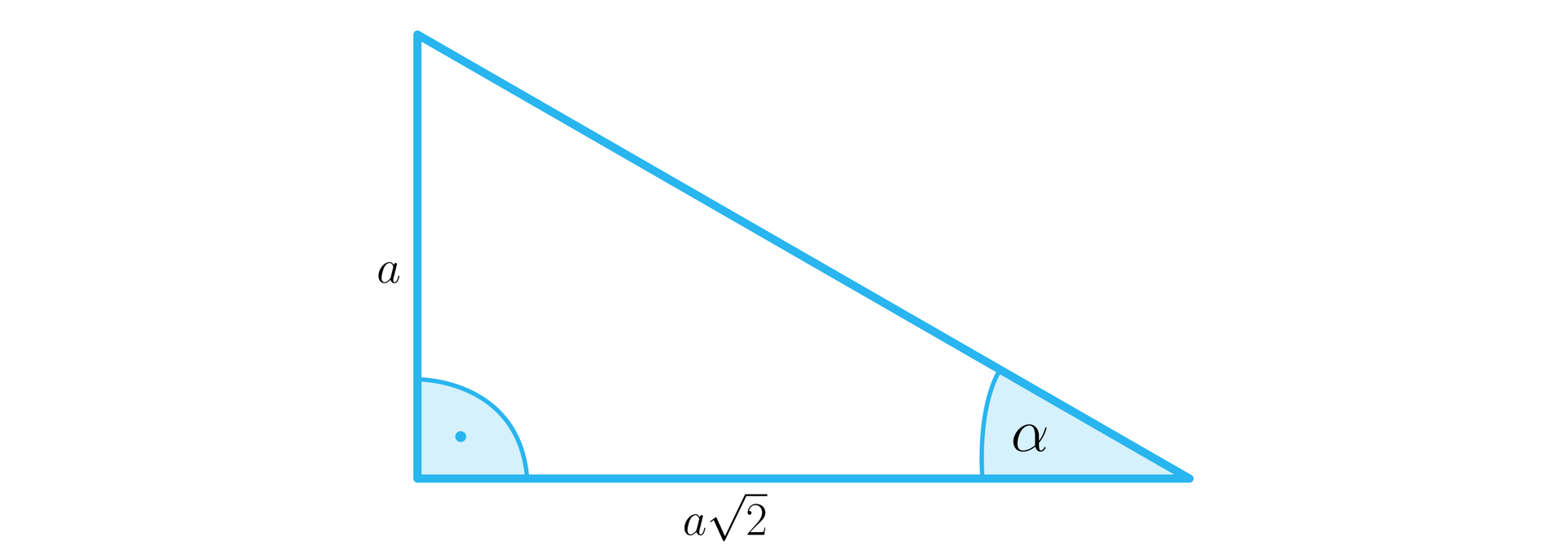
Połącz w pary wartość funkcji trygonometrycznej z przybliżoną wartością kąta .
<span aria-label="alfa, w przybliżeniu równe, trzydzieści pięć stopni" role="math"><math><mi>α</mi><mo>≈</mo><mn>35</mn><mo>°</mo></math></span>, <span aria-label="alfa, w przybliżeniu równe, dziewiętnaście stopni" role="math"><math><mi>α</mi><mo>≈</mo><mn>19</mn><mo>°</mo></math></span>, <span aria-label="alfa, w przybliżeniu równe, siedemdziesiąt dwa stopnie" role="math"><math><mi>α</mi><mo>≈</mo><mn>72</mn><mo>°</mo></math></span>, <span aria-label="alfa, w przybliżeniu równe, sześćdziesiąt dwa stopnie" role="math"><math><mi>α</mi><mo>≈</mo><mn>62</mn><mo>°</mo></math></span>
Uporządkuj wartości wyrażeń w kolejności malejącej:
1. , 2. , 3. , 4. , 5.
1. , 2. , 3. , 4. , 5.
1. , 2. , 3. , 4. , 5.
1. , 2. , 3. , 4. , 5.
Korzystając z tablic wartości funkcji trygonometrycznych, wstaw w odpowiednie miejsca przybliżone wartości:
, , , ,
............
............
............
............
............
Wiedząc o tym, że tangens kąta nachylenia prostej do osi układu współrzędnych jest równy współczynnikowi kierunkowemu prostej, wpisz przybliżone wartości kątów nachylenia podanych prostych do osi odciętych.
Jeżeli prosta jest określona równaniem , to kąt nachylenia tej prostej do osi odciętych wynosi ............ stopni.
Jeżeli prosta jest określona równaniem , to kąt nachylenia tej prostej do osi odciętych wynosi ............ stopni.
Jeżeli prosta jest określona równaniem , to kąt nachylenia tej prostej do osi odciętych wynosi ............ stopnie.
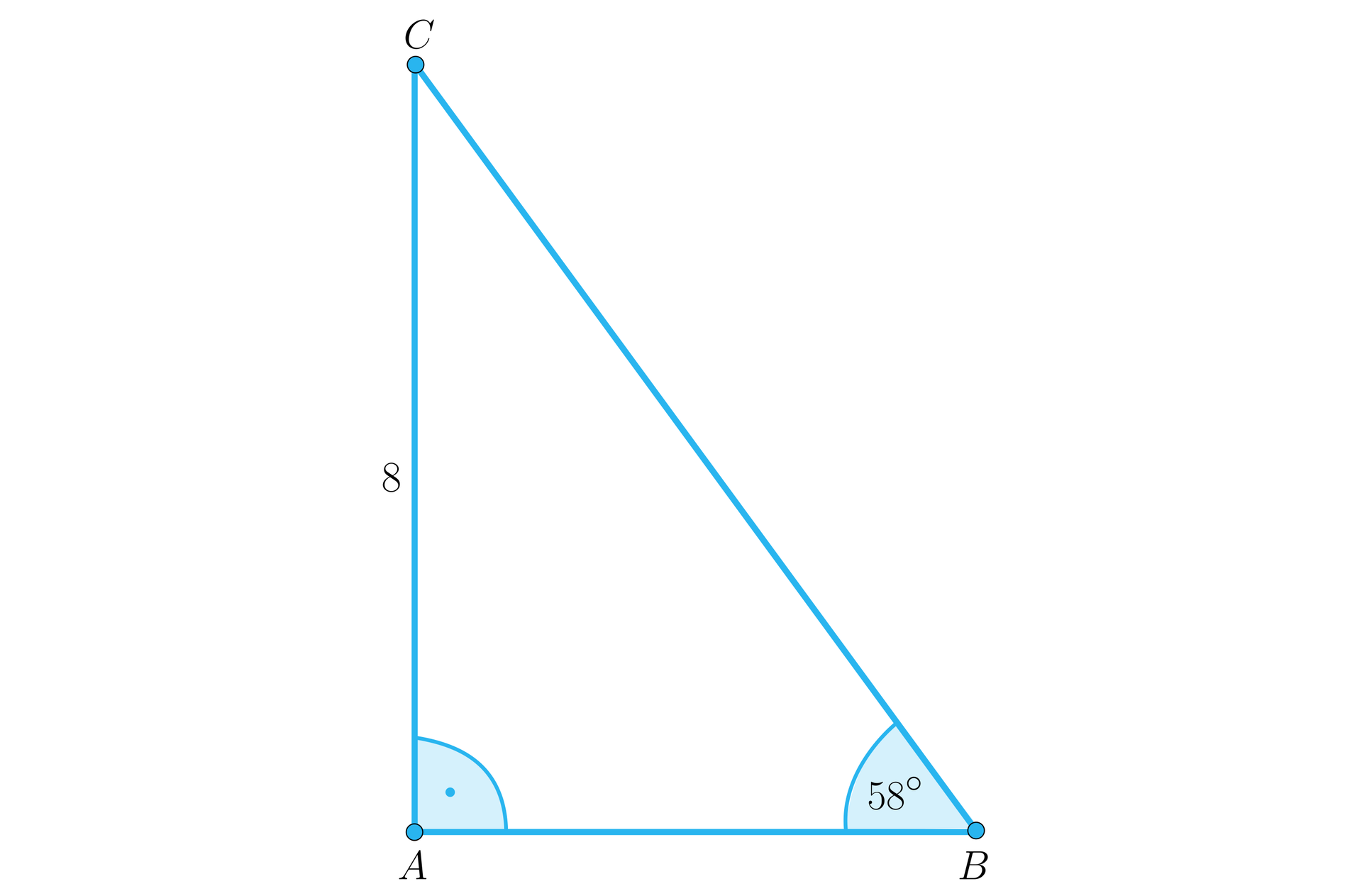
W trójkącie prostokątnym długość boku wynosi , a miara kąta wynosi . Wyznacz długości boków i miary pozostałych kątów tego trójkąta.
Wyznacz przybliżoną wartość kąta pomiędzy przekątną sześcianu a płaszczyzną jego podstawy.