Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Dany jest wykres funkcji

Rcvf0mION3B5M

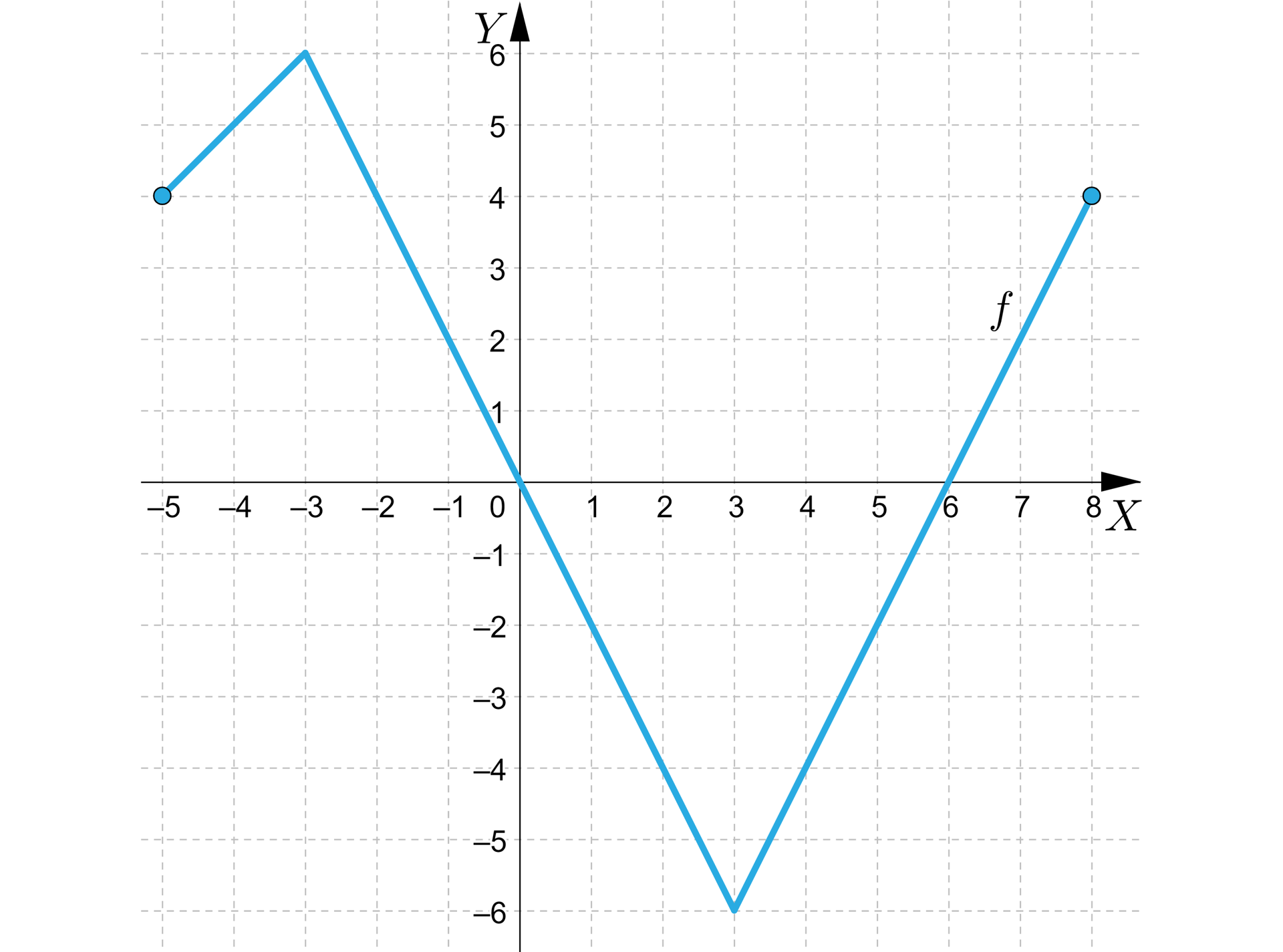
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 8 i pionową osią y od minus 6 do sześć. W układzie zaznaczono wykres funkcji f, który ma swój początek w zamalowanym punkcie nawias minus pięć średnik cztery zamknięcie nawiasu i biegnie ukośnie do punktu nawias minus trzy średnik sześć zamknięcie nawiasu, dalej biegnie również ukośnie do punktu nawias trzy średnik minus sześć, dalej biegnie ukośnie do zamalowanego punktu nawias osiem średnik cztery zamknięcie nawiasu.

REDfZOioNTaRR

Zaznacz poprawną odpowiedź. Zbiorem rozwiązań nierówności $f (x) \geq 2$ jest zbiór:

$"⟨"- 1, 7"⟩"$
$"⟨"- 1, 7")"$
$"⟨"- 5, - 1"⟩" \cup "⟨"7, 8")"$
$"⟨"- 5, - 1"⟩" \cup "⟨"7, 8"⟩"$

RD4cfF10OsZz2

Wybierz maksymalny przedział, w którym funkcja $f$ jest malejąca:

$"⟨"- 3, 3"⟩"$
$"⟨"- 5, 2"⟩"$
$"⟨"- 3, 3")"$

R1ErvzUHBdIi8

Wpisz poprawne liczby.

Największa wartość funkcji $f$ jest równa ............, a najmniejsza wartość funkcji $f$ jest równa .............

Ćwiczenie 2

Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

RZtveUZrdaC9p

R8xF67MB8LfCo

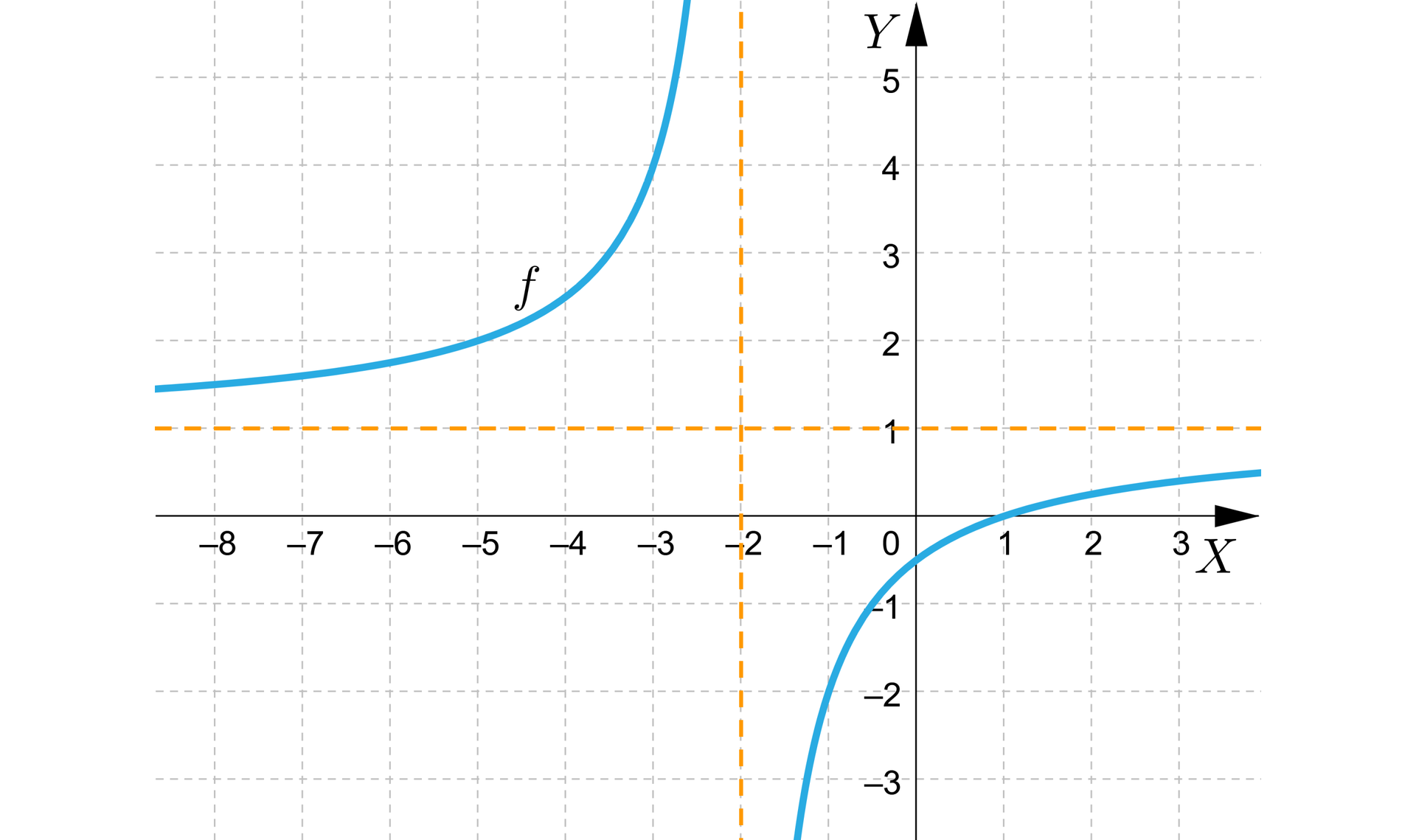
Zdanie	Prawda	Fałsz
Funkcja jest rosnąca w całej dziedzinie.	□	□
Funkcja jest różnowartościowa.	□	□
Dziedziną funkcji jest $D_{f} = ℝ ∖ "{"- 2"}"$ .	□	□
Zbiór wartości funkcji $Z W = ℝ ∖ "{"1"}"$ .	□	□

Ćwiczenie 3

Na rysunku przedstawiono wykres funkcji $f$ .

RCKB26XkvTKh1

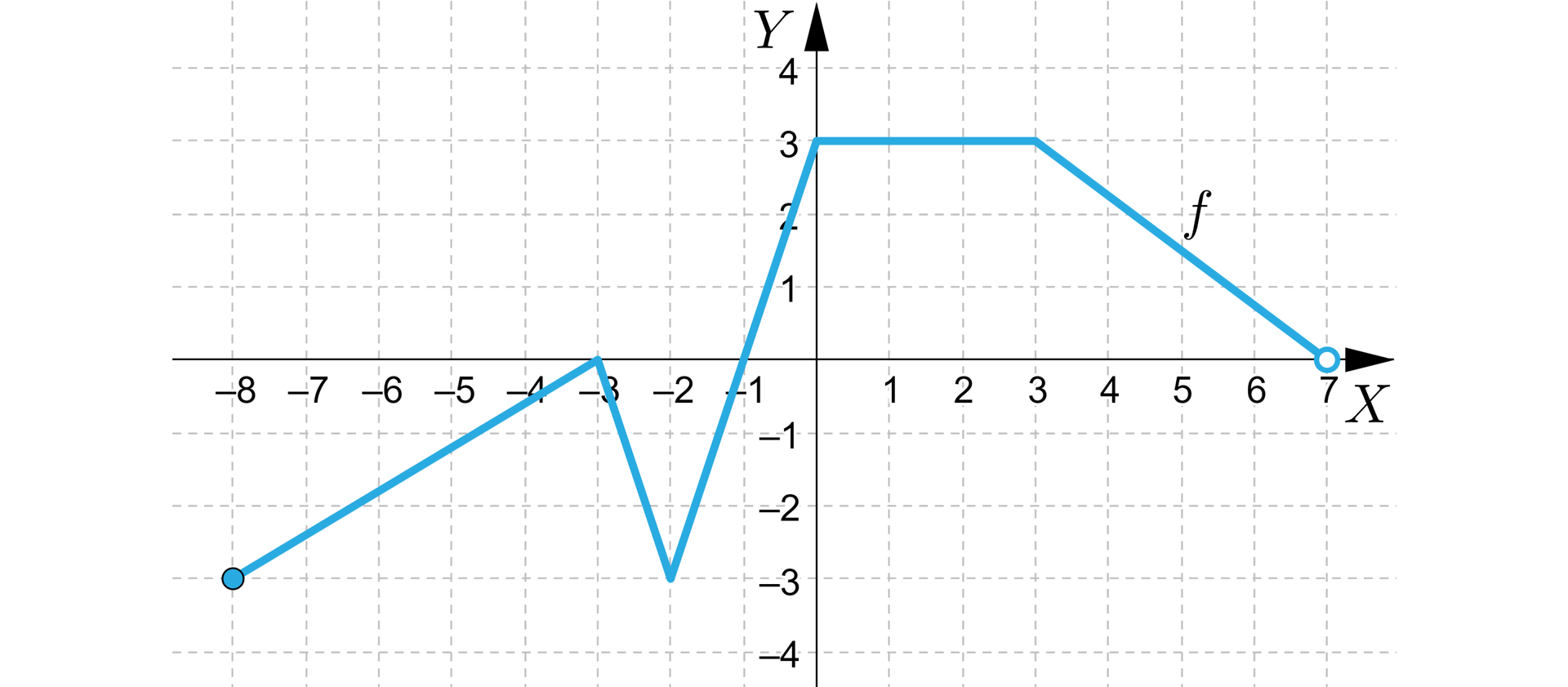
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 8 do 7 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji f, który ma swój początek w zamalowanym punkcie nawias minus osiem średnik minus trzy zamknięcie nawiasu i biegnie ukośnie do punktu nawias minus trzy średnik zero zamknięcie nawiasu, dalej biegnie również ukośnie do punktu nawias minus dwa średnik minus trzy, dalej biegnie ukośnie do punktu nawias zero średnik trzy zamknięcie nawiasu, stąd biegnie poziomo do punktu nawias trzy średnik trzy zamknięcie nawiasu i dalej biegnie ukośnie do niezamalowanego punktu nawias siedem średnik zero zamknięcie nawiasu.

R1e4BHli1x1Bg

Dostępne opcje do wyboru:

x = - 3

⟨0, 7)

⟨3, 7)

⟨- 8, - 3)

⟨0, 3⟩

(- 1, 7)

⟨- 2, 0⟩

⟨- 3, 3⟩

⟨- 2, 3⟩

x = - 1

⟨- 8, - 3⟩

(- 3, - 1)

⟨0, 3⟩

⟨- 3, - 2⟩

⟨- 8, 7)

. Polecenie: Przeciągnij odpowiednie elementy, aby powstał poprawny opis własności funkcji. - dziedzina funkcji

D_{f} =

luka do uzupełnienia ,
- zbiór wartości

f (D) =

luka do uzupełnienia ,
- miejsca zerowe funkcji luka do uzupełnienia , luka do uzupełnienia ,
- funkcja przyjmuje wartości dodatnie dla

x \in

luka do uzupełnienia ,
- funkcja przyjmuje wartości ujemne dla

x \in

luka do uzupełnienia

\cup

luka do uzupełnienia ,
- funkcja jest rosnąca w przedziale luka do uzupełnienia oraz luka do uzupełnienia ,
- funkcja jest malejąca w przedziałach: luka do uzupełnienia oraz luka do uzupełnienia ,
- funkcja jest stała w przedziale luka do uzupełnienia ,
- funkcja jest nierosnąca w przedziale luka do uzupełnienia ,
- funkcja jest niemalejąca w przedziale luka do uzupełnienia ,
- funkcja ma wartością najmniejszą

y = - 3

dla

x = - 8

lub

x = - 2

, funkcja ma wartością największą

y = 3

dla

x \in

luka do uzupełnienia .

Przeciągnij odpowiednie elementy, aby powstał poprawny opis własności funkcji:

$(- 3, - 1)$ , $y = 3$ , $x = - 3$ , $x = - 1$ , $x = - 2$ , $"⟨"- 3, - 2"⟩"$ , $"⟨"- 8, - 3"⟩"$ , $y = - 3$ , $"⟨"- 3, 3"⟩"$ , $"⟨"- 2, 0"⟩"$ , $(- 1, 7)$ , $x = - 8$ , $x \in "⟨"0, 3"⟩"$ , $"⟨"- 8, - 3")"$ , $"⟨"- 8, 7")"$ , $"⟨"0, 3"⟩"$ , $"⟨"3, 7")"$

- dziedzina funkcji $D_{f} =$ ,
- zbiór wartości $f (D) =$ ,
- miejsca zerowe funkcji , ,
- funkcja przyjmuje wartości dodatnie dla $x \in$ ,
- funkcja przyjmuje wartości ujemne dla $x \in$ $\cup$ ,
- funkcja jest rosnąca w przedziale oraz ,
- funkcja jest malejąca w przedziałach: oraz ,
- funkcja jest stała w przedziale ,
- funkcja ma wartością najmniejszą dla lub , funkcja ma wartością największą dla .

Ćwiczenie 4

Na rysunku przedstawiono wykres funkcji $f : ℝ \to ℝ$ określonej wzorem:

$f (x) = \{\begin{cases} 3 & dla x \in (- \infty, - 1) \\ |x - 2| & dla x \in ⟨- 1, 6) \\ - 2 & dla x \in ⟨6, \infty) \end{cases}$ .

RLWus3cN11UiM

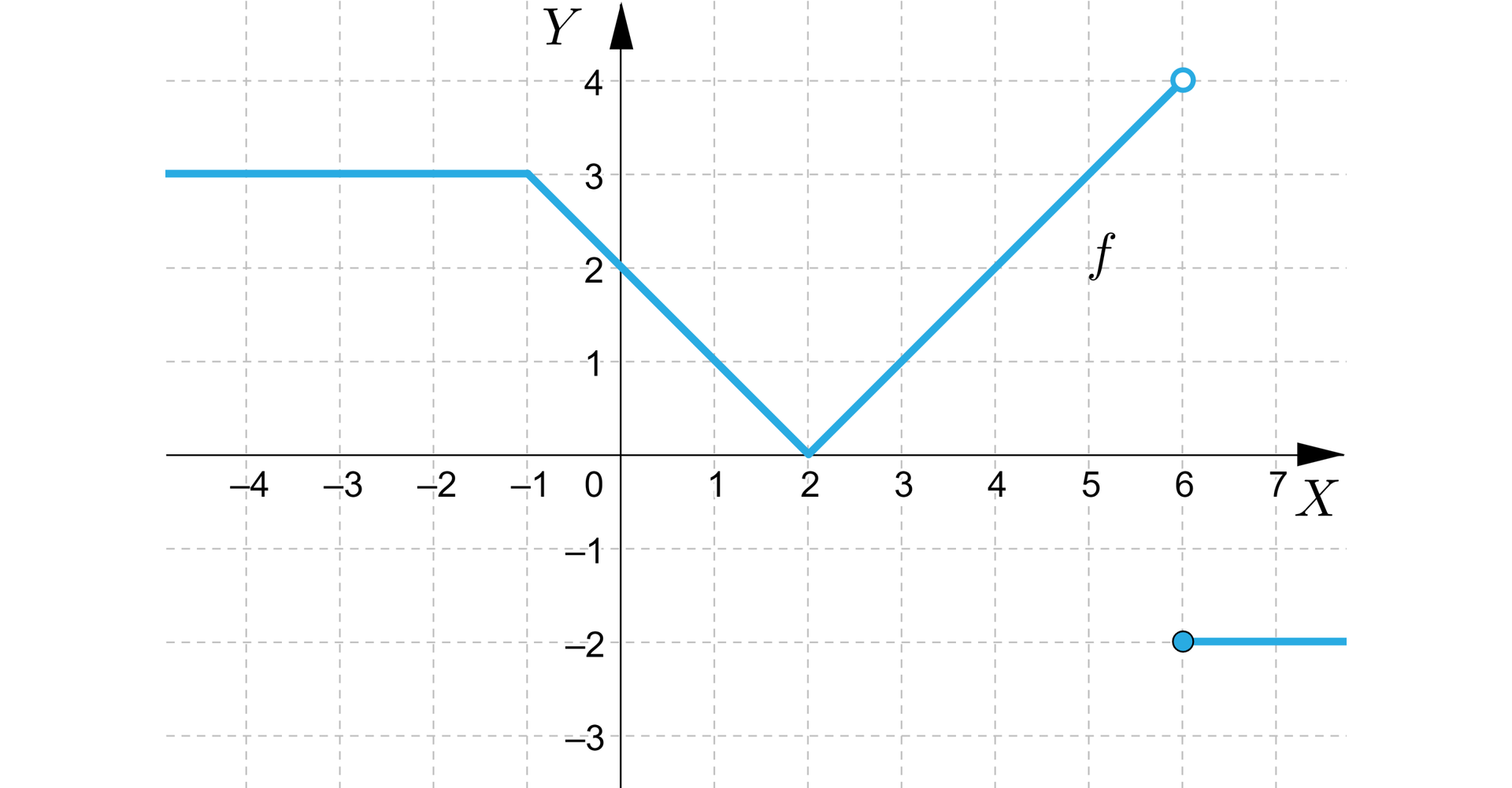
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 7 i pionową osią y od minus 3 do cztery. W układzie zaznaczono wykres funkcji f, który pojawia się w trzeciej ćwiartce i biegnie poziomo do punktu nawias minus jeden średnik trzy zamknięcie nawiasu, dalej biegnie ukośnie do punktu nawias dwa średnik zero zamknięcie nawiasu, dalej biegnie również ukośnie do niezamalowanego punktu nawias sześć średnik cztery. Druga część ma swój początek w zamalowanym punkcie nawias sześć średnik minus dwa i biegnie poziomo aż wychodzi poza płaszczyznę układu w czwartej ćwiartce.

RHs3z5L4YSLkN

Połącz w odpowiednie pary: zbiór rozwiązań równania

f (x) = 3

to Możliwe odpowiedzi: 1.

(- \infty, - 1⟩ \cup \{5\}

, 2.

(- \infty, 6)

, 3.

⟨1, 3⟩ \cup ⟨6, \infty)

, 4.

⟨6, \infty)

zbiór rozwiązań nierówności

f (x) \geq 0

to Możliwe odpowiedzi: 1.

(- \infty, - 1⟩ \cup \{5\}

, 2.

(- \infty, 6)

, 3.

⟨1, 3⟩ \cup ⟨6, \infty)

, 4.

⟨6, \infty)

zbiór rozwiązań równania

f (x) = - 2

to Możliwe odpowiedzi: 1.

(- \infty, - 1⟩ \cup \{5\}

, 2.

(- \infty, 6)

, 3.

⟨1, 3⟩ \cup ⟨6, \infty)

, 4.

⟨6, \infty)

zbiór rozwiązań nierówności

f (x) \leq 1

to Możliwe odpowiedzi: 1.

(- \infty, - 1⟩ \cup \{5\}

, 2.

(- \infty, 6)

, 3.

⟨1, 3⟩ \cup ⟨6, \infty)

, 4.

⟨6, \infty)

Połącz w pary:

zbiór rozwiązań równania $f (x) = 3$ to
zbiór rozwiązań nierówności $f (x) \geq 0$ to
zbiór rozwiązań równania $f (x) = - 2$ to
zbiór rozwiązań nierówności $f (x) \leq 1$ to

Ćwiczenie 5

RmWhlxxI1yLKr

R1U9VY1YqOSFi

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 4 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji f, który składa się z dwóch części. Pierwsza ma swój początek w punkcie nawias minus cztery średnik jeden zamknięcie nawiasu i biegnie ukośnie do niezamalowanego punktu nawias minus jeden średnik dwa zamknięcie nawiasu. Druga część ma swój początek w zamalowanym punkcie nawias minus jeden średnik minus dwa i biegnie ukośnie do zamalowanego punktu nawias cztery średnik jeden zamknięcie nawiasu. Możliwe odpowiedzi: 1.

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 4 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji f, która ma swój początek w zamalowanym punkcie nawias minus cztery średnik jeden zamkniecie nawiasu, dalej biegnie ukośnie do punktu nawias minus dwa średnik dwa zamknięcie nawiasu, dalej biegnie również ukośnie do punkcie nawias dwa średnik minus dwa zamkniecie nawiasu, z tego punktu biegnie ukośnie do niezamalowanego punktu nawias cztery średnik dwa zamknięcie nawiasu. Możliwe odpowiedzi: 1.

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 4 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji f, która ma kształt litery V, jej wierzchołek znajduje się w punkcie nawias zero średnik minus dwa zamknięcie nawiasu, lewe ramię przechodzi przez punkt nawias minus dwa średnik jeden zamknięcie nawiasu, a prawe ramię przechodzi przez punkt nawias dwa średnik jeden zamknięcie nawiasu. Możliwe odpowiedzi: 1.

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 4 i pionową osią y od minus 4 do cztery. W układzie zaznaczono wykres funkcji f, która ma swój początek w niezamalowanym punkcie nawias minus cztery średnik minus cztery zamknięcie nawiasu i biegnie poziomo do punktu nawias minus cztery średnik minus dwa zamknięcie nawiasu, dalej biegnie ukośnie do punktu nawias zero średnik dwa zamknięcie nawiasu dalej biegnie poziomo do niezamalowanego punktu nawias cztery średnik dwa zamknięcie nawiasu. Możliwe odpowiedzi: 1.

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

⟨ - 2, 2)

, 2.

<mfenced open="<"> - 2, \infty

, 3.

<mfenced open="<" close=">"> - 4, 2

, 4.

<mfenced open="<" close=">"> - 2, 2

Ćwiczenie 6

Dany jest wykres funkcji:

RFYCuOzcaQ1wJ

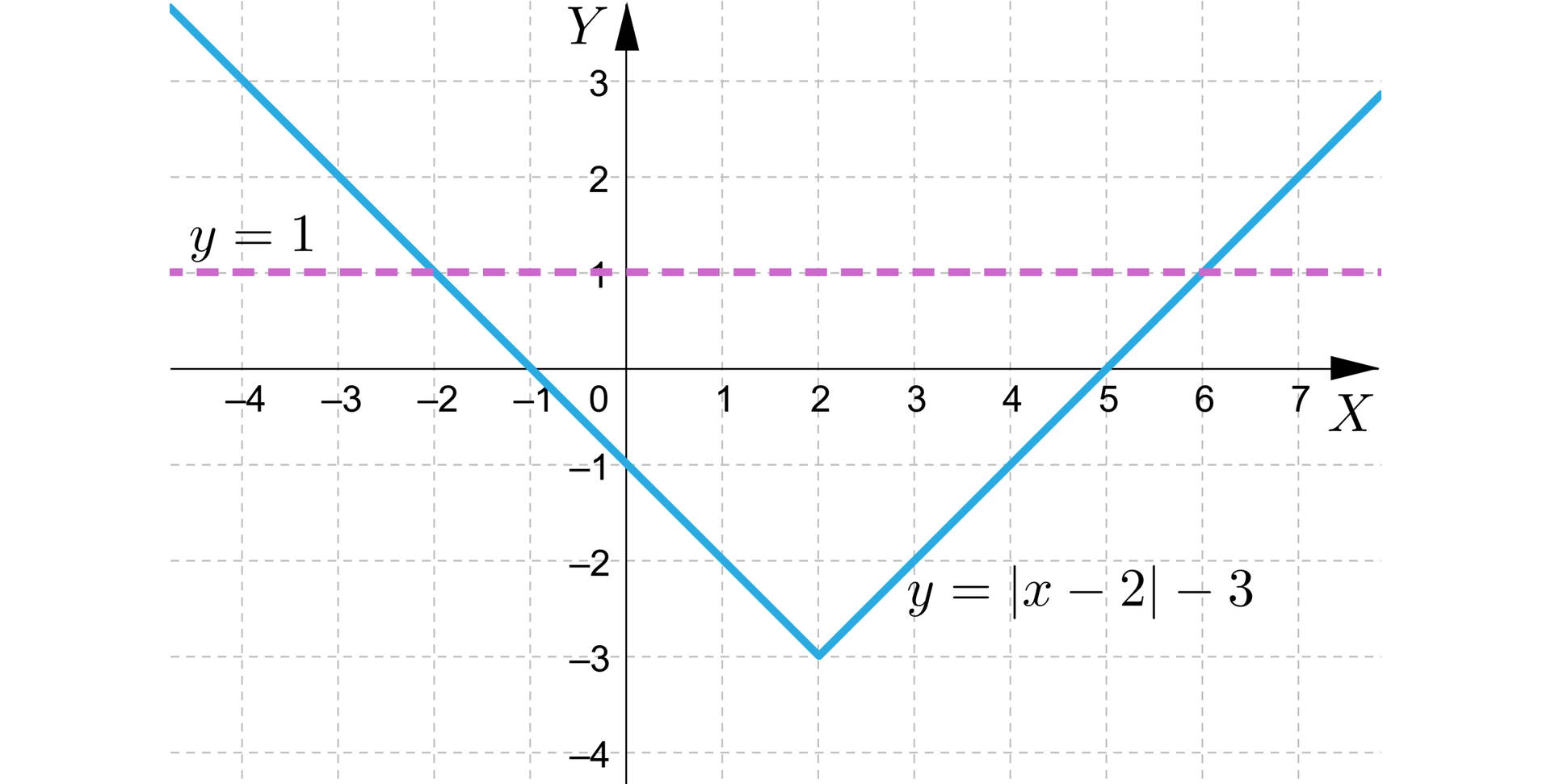
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 7 i pionową osią y od minus 4 do trzy. W układzie zaznaczono wykres funkcji y=x−2−3, która ma kształt litery V, jej wierzchołek znajduje się w punkcie nawias dw średnik minus trzy zamknięcie nawiasu, lewe ramię przechodzi przez punkt nawias minus dwa średnik jeden zamknięcie nawiasu, a prawe ramię przechodzi przez punkt nawias sześć średnik jeden zamknięcie nawiasu. W układzie linią przerywaną zaznaczono poziomą prostą o równaniu y=1.

R1Ly828JuruxJ

Łączenie par. Zaznacz, czy zdanie jest prawdziwe, czy fałszywe.. Funkcja posiada trzy miejsca zerowe.. Możliwe odpowiedzi: Prawda, Fałsz.

f (x) > 1

dla

x \in (- \infty, - 2) \cup (6, \infty)

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest rosnąca tylko w przedziale

⟨2, 5⟩

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest malejąca w przedziale

(- \infty, 2⟩

.. Możliwe odpowiedzi: Prawda, Fałsz.

f (x) = 0

dla

x = - 1

lub

x = 5

.. Możliwe odpowiedzi: Prawda, Fałsz. Zbiór wartości funkcji to

Z W = ⟨- 3, \infty)

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja jest różnowartościowa.. Możliwe odpowiedzi: Prawda, Fałsz

Zaznacz, czy zdanie jest prawdziwe, czy fałszywe.

Zdanie	Prawda	Fałsz
Funkcja posiada trzy miejsca zerowe.	□	□
$f (x) > 1$ dla $x \in (- \infty, - 2) \cup (6, \infty)$ .	□	□
Funkcja jest rosnąca tylko w przedziale $"⟨"2, 5"⟩"$ .	□	□
Funkcja jest malejąca w przedziale $"("- \infty, 2"⟩"$ .	□	□
$f (x) = 0$ dla $x = - 1$ lub $x = 5$ .	□	□
Zbiór wartości funkcji to $Z W = "⟨"- 3, \infty")"$ .	□	□
Funkcja jest różnowartościowa.	□	□

Ćwiczenie 7

Na rysunku przedstawiono wykres funkcji $f : (- 5, 4) \to ℝ$ .

RGL1g3HVnlRLY

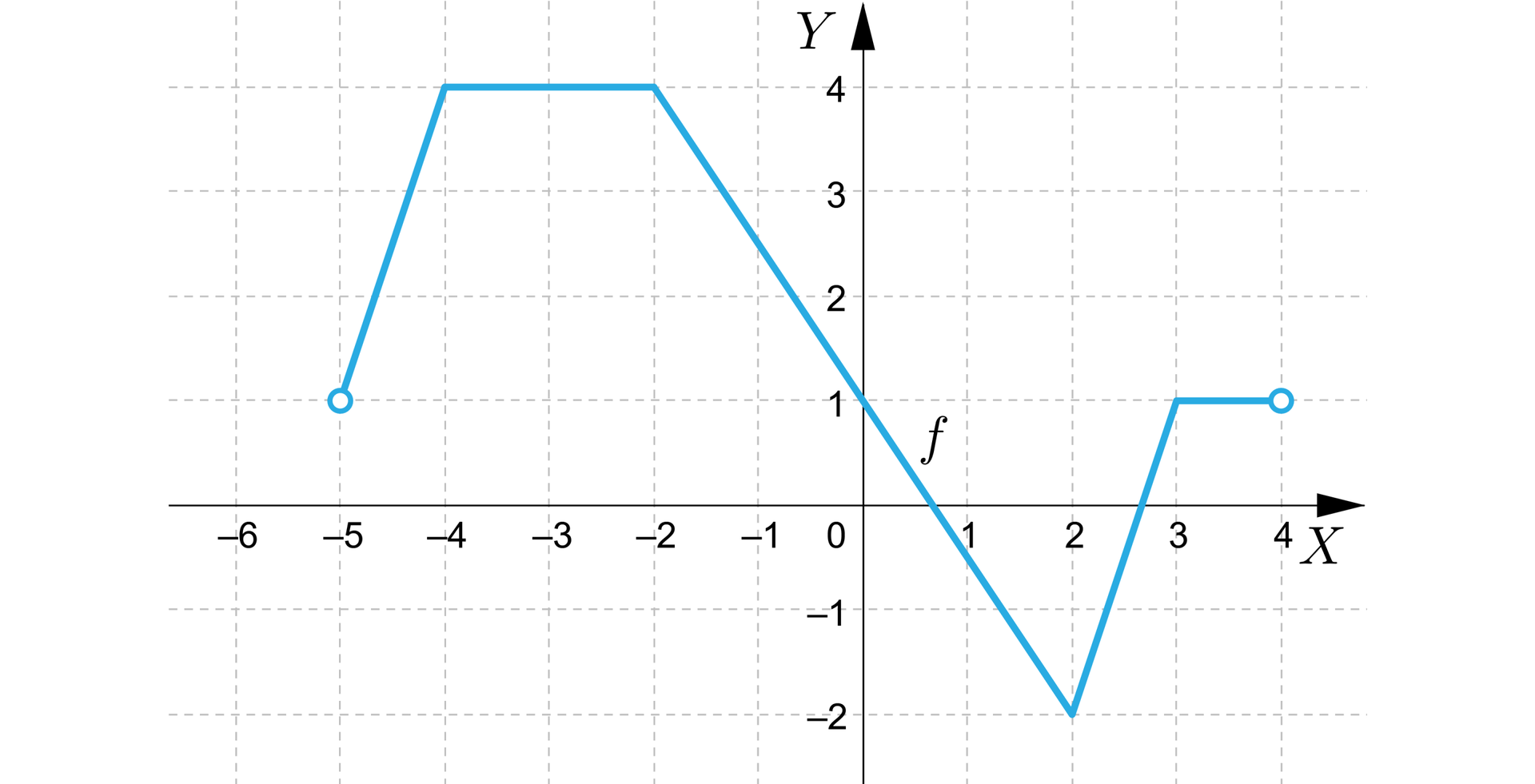
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 6 do 4 i pionową osią y od minus 2 do cztery. W układzie zaznaczono wykres funkcji f, która ma swój początek w niezamalowanym punkcie nawias minus pięć średnik jeden zamknięcie nawiasu i biegnie ukośnie do punktu nawias minus cztery średnik cztery zamknięcie nawiasu, dalej biegnie poziomo do punktu nawias minus dwa średnik cztery zamknięcie nawiasu dalej biegnie ukośnie do punktu nawias dwa średnik minus dwa zamknięcie nawiasu, dalej biegnie znów ukośnie do punktu nawias trzy średnik jeden jeden zamknięcie nawiasu stąd biegnie poziomo do niezamalowanego punktu nawias cztery średnik jeden zamknięcie nawiasu.

RNwJ8ueJ7tf7N

Zaznacz wszystkie zdania prawdziwe.

Funkcja $f$ jest rosnąca dla $x \in "("- 5, - 4"⟩"$ .
Funkcja $f$ jest malejąca dla $x \in "⟨"- 2, - 2"⟩"$ .
Funkcja $f$ jest stała dla $x \in "⟨"- 4, - 2"⟩"$ .
Funkcja jest monotoniczna.

Ćwiczenie 8

Na rysunku przedstawiono wykresy funkcji $f (x) = \frac{1}{4} x^{2}$ , $g (x) = |x|$ .

RTsYwIZsQWhxw

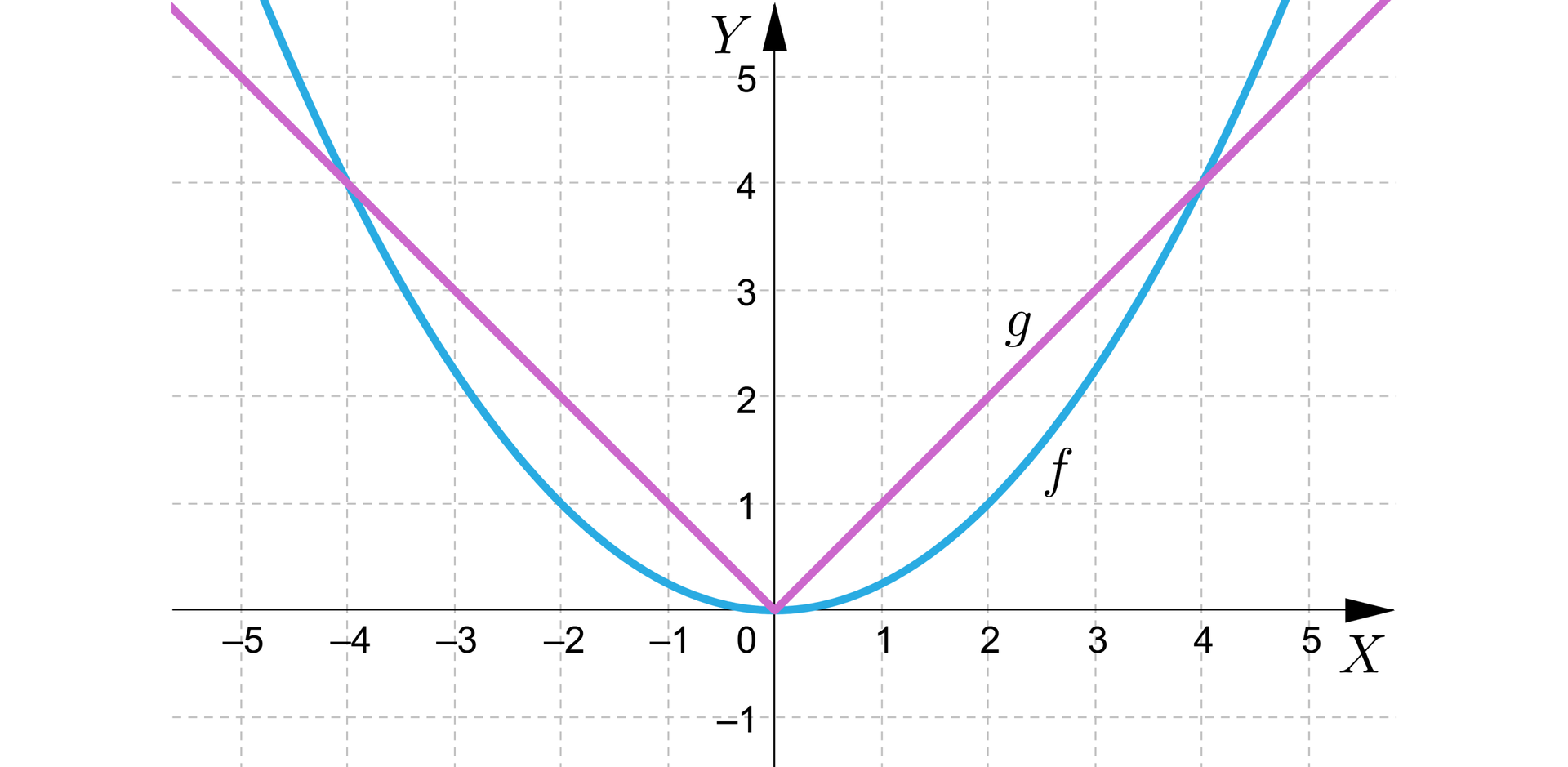
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 5 i pionową osią y od minus 1 do pięć. W układzie zaznaczono dwa wykresy. Pierwszy to wykres funkcji f, która ma ma kształt paraboli o ramionach skierowanych do góry, jej wierzchołek znajduje się w środku układu współrzędnych. Drugi wykres g ma kształt litery V, której wierzchołek również znajduje się w środku układu współrzędnych. Wykresy przecinają się w punktach nawias minus cztery średnik cztery zamknięcie nawiasu i nawias cztery średnik cztery zamknięcie nawiasu.

Odczytaj z wykresu i zapisz:

zbiór rozwiązań równania $f (x) = g (x)$ ,

zbiór rozwiązań nierówności $f (x) < g (x)$ ,

zbiór rozwiązań nierówności $f (x) \geq g (x)$ .

$f (x) = g (x)$ dla $x = - 4$ , $x = 0$ , $x = 4$ ,

$f (x) < g (x)$ dla $x \in (- 4, 0) \cup (0, 4)$ ,

$f (x) \geq g (x)$ dla $x \in (- \infty, - 4⟩ \cup ⟨4, \infty)$ .

Ćwiczenie 9

Na rysunku przedstawiono wykresy funkcji $f (x) = x^{2}$ oraz $g (x) = 2 - x$ .

RpX9saNj2Qqxn

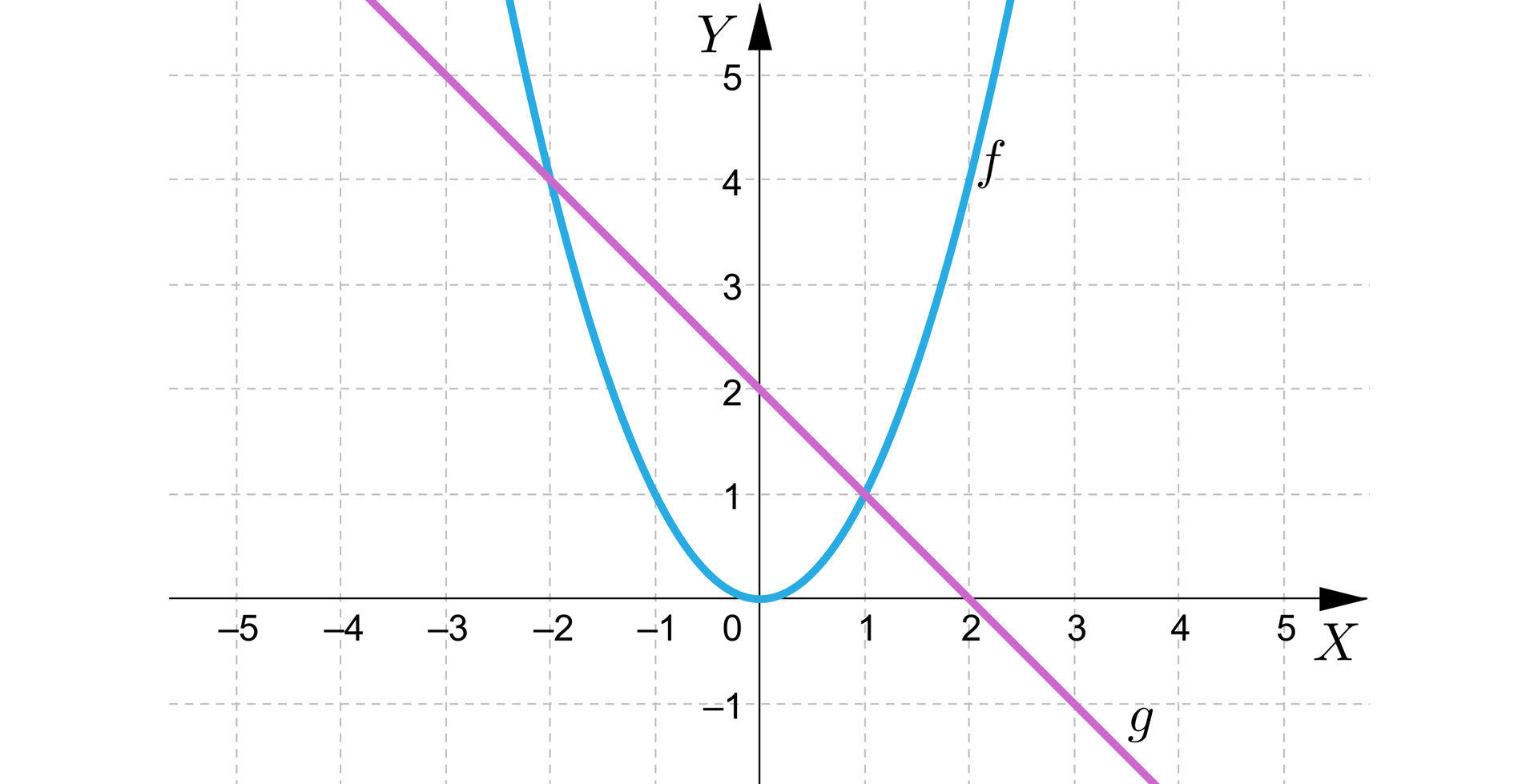
Odczytaj z wykresu rozwiązanie równania $x^{2} = 2 - x$ oraz nierówności $x^{2} \geq 2 - x$ .

$x^{2} = 2 - x$ dla $x = - 2$ lub $x = 1$ .

$x^{2} \geq 2 - x$ dla $x \in (- \infty, - 2⟩ \cup ⟨1, \infty)$ .

Animacja

Dla nauczyciela