Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

R11QRlZaEvXVx

R16zT9OznY9Et

Spośród podanych możliwości wybierz miejsca zerowe w kolejności rosnącej oraz asymptotę wykresu funkcji

y = \log_{2} |x + 3|

. Miejsca zerowe funkcji to: 1.

(2; 0)

, 2.

x = - 3

, 3.

(- 2; 0)

, 4.

(- 4; 0)

, 5.

(4; 0)

, 6.

(- 3; 0)

, 7.

x = 0

, 8.

(3; 0)

, 9.

x = 3

oraz 1.

(2; 0)

, 2.

x = - 3

, 3.

(- 2; 0)

, 4.

(- 4; 0)

, 5.

(4; 0)

, 6.

(- 3; 0)

, 7.

x = 0

, 8.

(3; 0)

, 9.

x = 3

.
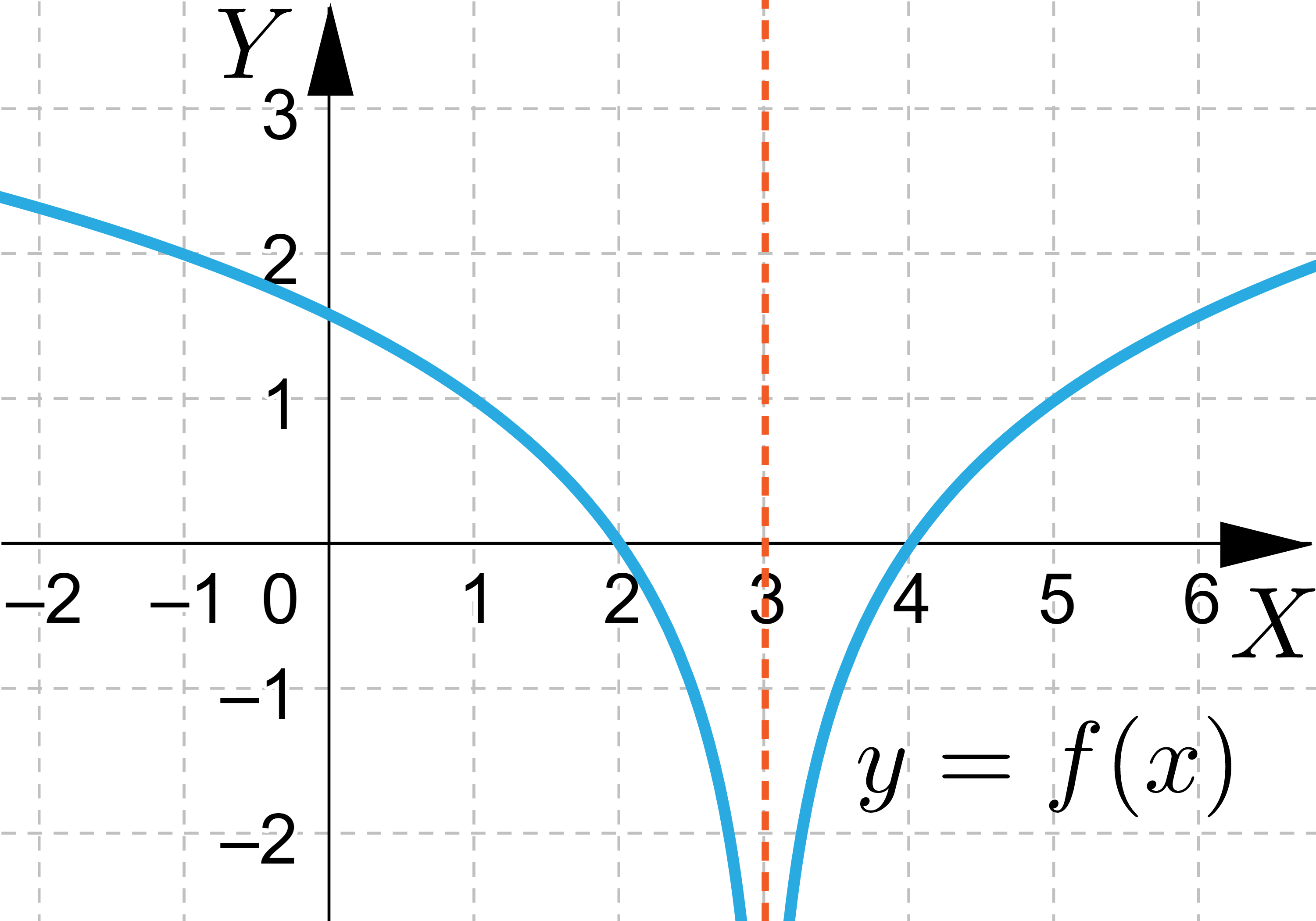
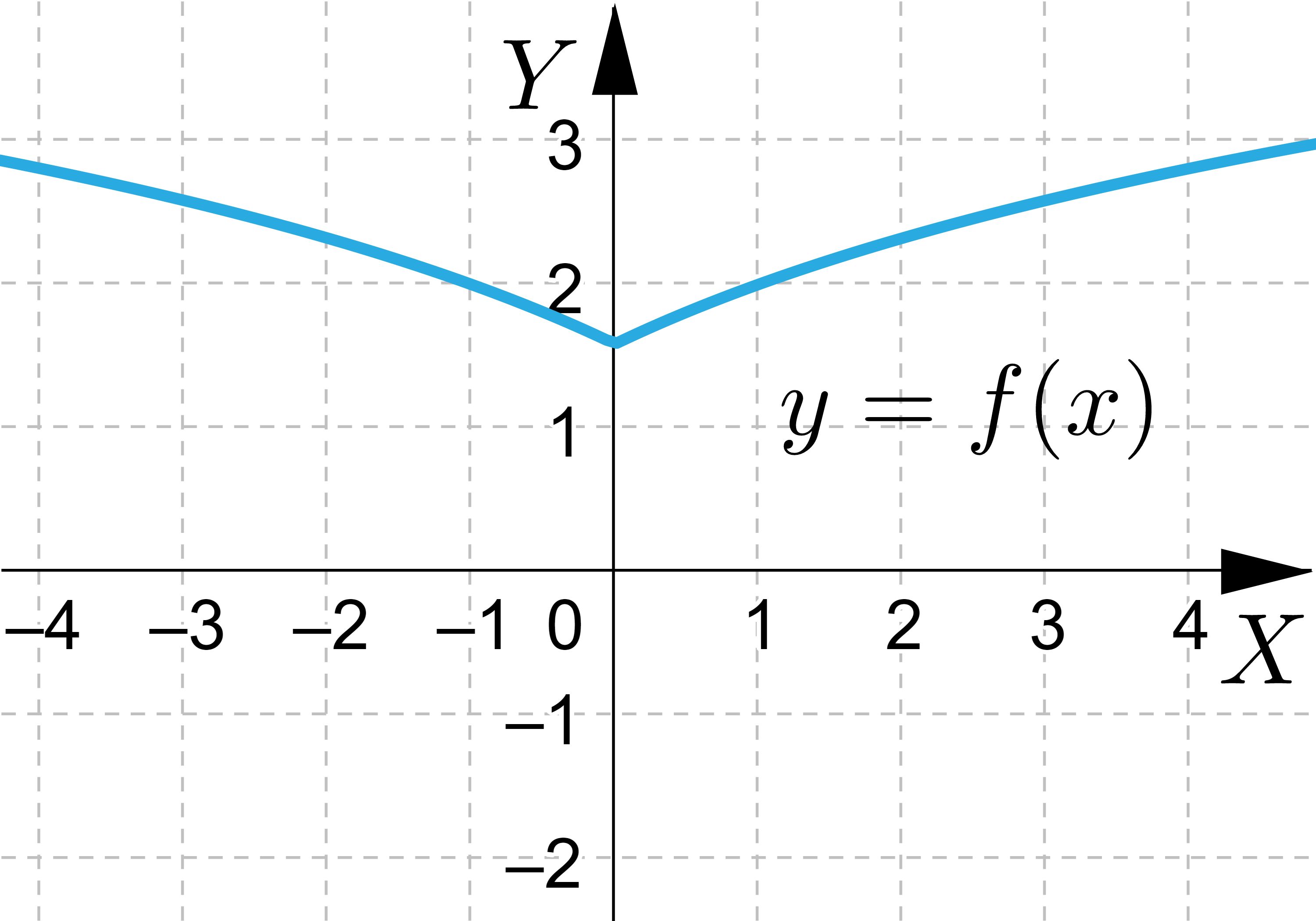
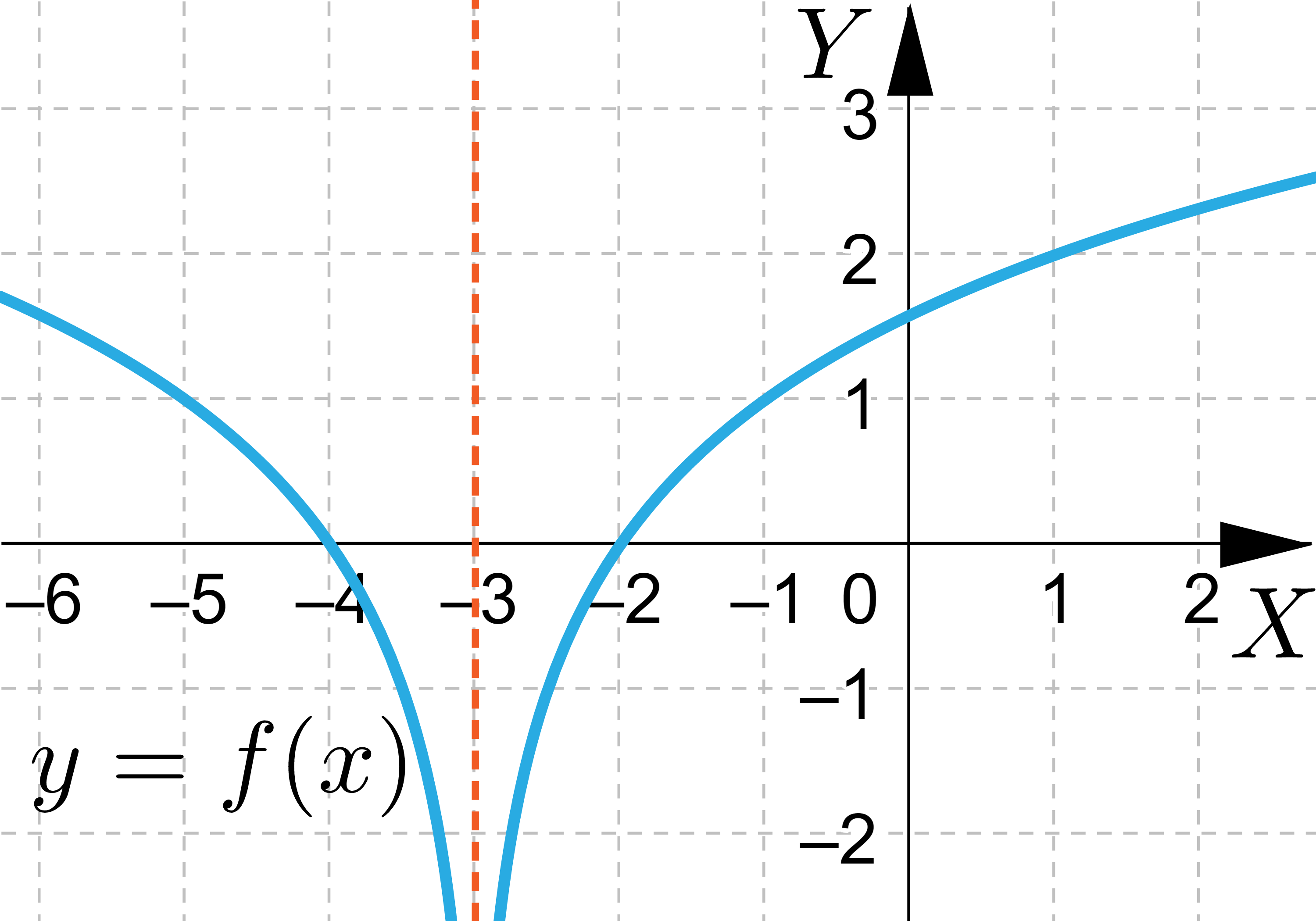
Asymptota funkcji ma równanie 1.

(2; 0)

, 2.

x = - 3

, 3.

(- 2; 0)

, 4.

(- 4; 0)

, 5.

(4; 0)

, 6.

(- 3; 0)

, 7.

x = 0

, 8.

(3; 0)

, 9.

x = 3

Ćwiczenie 2

R4r9S7fnaoB5U

R2hxxJbvFQs6u

Ćwiczenie 3

Na podstawie wykresu funkcji $f (x) = \log_{\frac{1}{3}} x$ przedstawionej na wykresie wybierz zdania prawdziwe.

R1QZlQeggOQrI

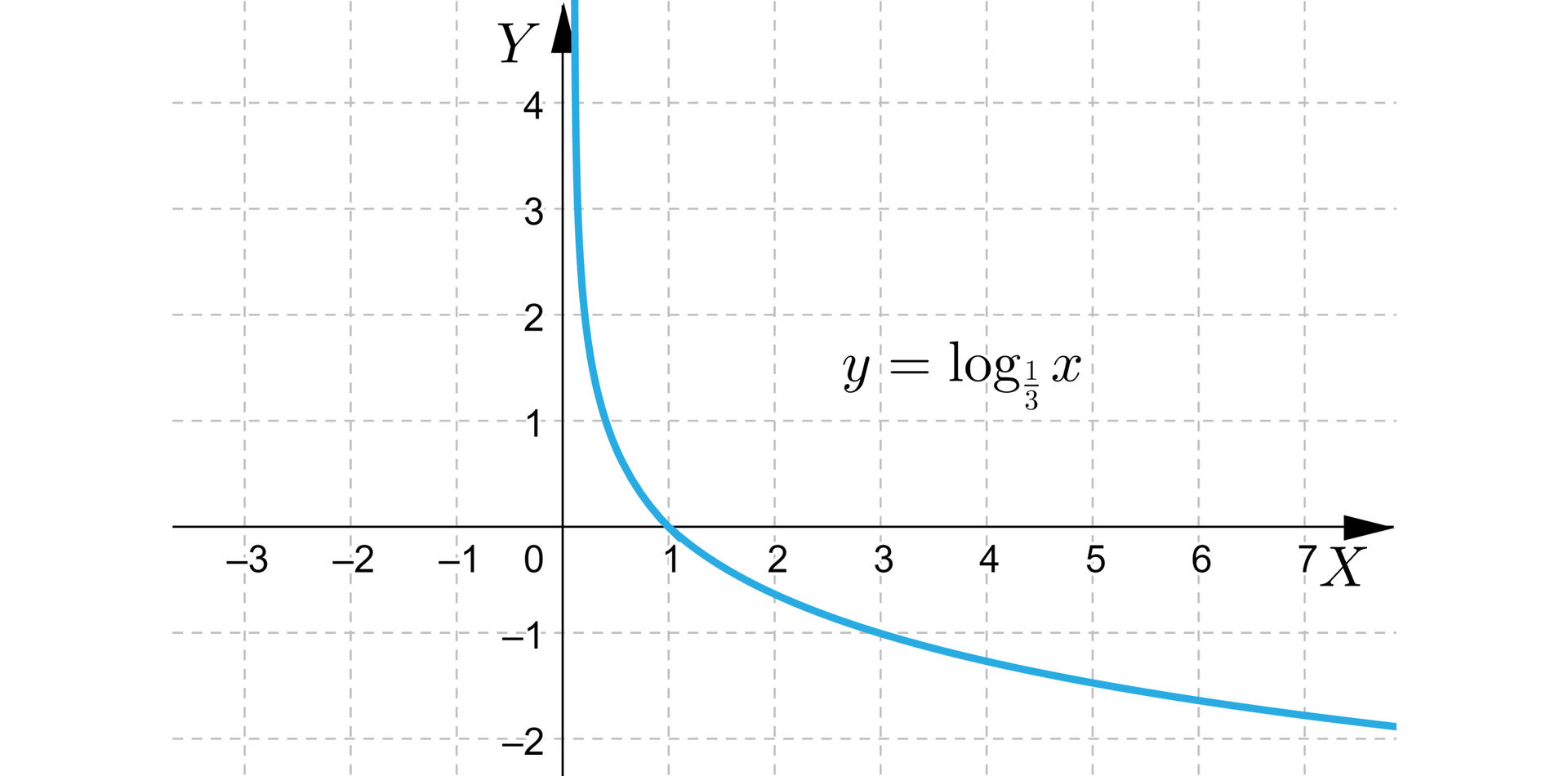
Na podstawie wzoru funkcji $f (x) = \log_{\frac{1}{3}} x$ wybierz zdania prawdziwe.

RVkhaDXOpzDpH1

Wykres funkcji $y = \log_{\frac{1}{3}} "|"x + 3"|" + 2$ przecina oś $Y$ w punkcie $(0, 1)$ .
Wykres funkcji $y = \log_{\frac{1}{3}} "|"x + 3"|" + 2$ przecina oś $X$ tylko w punkcie $(6, 0)$ .
Wykres funkcji $y = \log_{\frac{1}{3}} "|"x + 3"|" + 2$ jest symetryczny względem prostej $x = 3$ .
Funkcja $y = \log_{\frac{1}{3}} "|"x + 3"|" + 2$ jest malejąca tylko dla $x \in (- 3, + \infty)$ .

Ćwiczenie 4

Dana jest funkcja $f (x) = \log_{\frac{1}{3}} x$ przedstawiona na wykresie.

R1QZlQeggOQrI

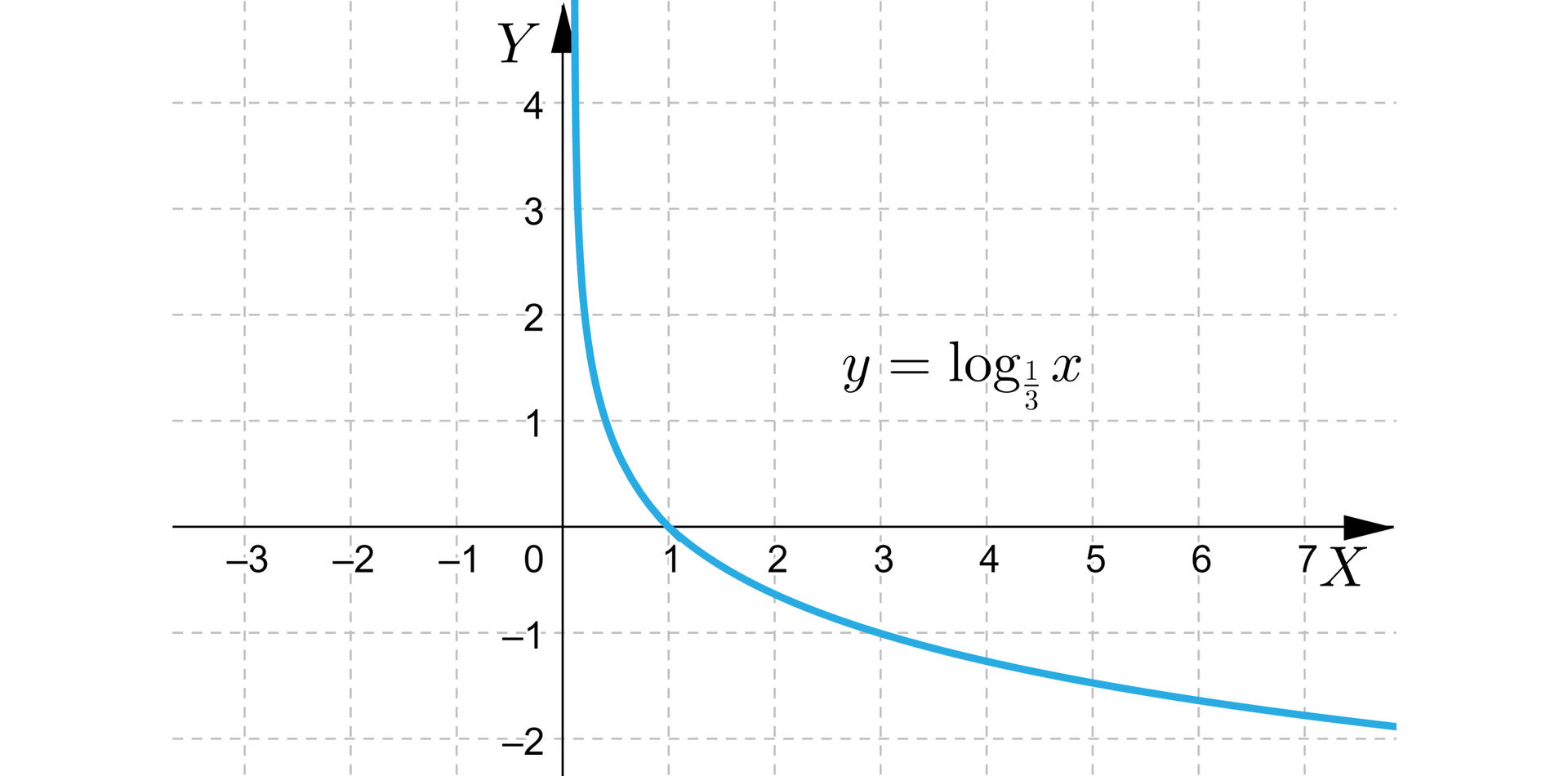
Dana jest funkcja $f (x) = \log_{\frac{1}{3}} x$ . Na podstawie jej wzoru, wykonaj poniższe ćwiczenie.

R1Hr1XgtnEjzn

Dana jest funkcja

f (x) = \log_{\frac{1}{3}} x

. Na podstawie wykresu tej funkcji (przedstawionego w zadaniu powyżej), uzupełnij pola, upuszczając na nie odpowiednie liczby całkowite podane poniżej. Wykres funkcji

y = \log_{\frac{1}{3}} (|x| + 3) + 2

przecina oś

Y

w punkcie

(0,

- 6

, 2.

- 2

, 3.

0

, 4.

- 1

, 5.

1

, 6.

- 3

, 7.

2

, 8.

6

, 9.

3

)

.

Miejsca zerowe funkcji

y = \log_{\frac{1}{3}} (|x| + 3)

x =

- 6

, 2.

- 2

, 3.

0

, 4.

- 1

, 5.

1

, 6.

- 3

, 7.

2

, 8.

6

, 9.

3

oraz

x =

- 6

, 2.

- 2

, 3.

0

, 4.

- 1

, 5.

1

, 6.

- 3

, 7.

2

, 8.

6

, 9.

3

.

Funkcja

y = \log_{\frac{1}{3}} (|x| + 3)

jest malejąca dla

x \in (

- 6

, 2.

- 2

, 3.

0

, 4.

- 1

, 5.

1

, 6.

- 3

, 7.

2

, 8.

6

, 9.

3

, + \infty)

Uzupełnij pola, upuszczając na nie odpowiednie liczby całkowite podane poniżej.

$1$ , $- 1$ , $0$ , $2$ , $- 2$ , $3$ , $- 3$ , $6$

Wykres funkcji $y = \log_{\frac{1}{3}} ("|"x"|" + 3) + 2$ przecina oś $Y$ w punkcie $(0,$ ............ $)$ .

Miejsca zerowe funkcji $y = \log_{\frac{1}{3}} ("|"x"|" + 3) + 2$ to $x = - 6$ oraz $x =$ .............

Funkcja $y = \log_{\frac{1}{3}} ("|"x"|" + 3) + 2$ jest malejąca dla $x \in ($ ............ $, + \infty)$ .

RNmFdlinSzQVM2

Ćwiczenie 5

Wybierz wzór funkcji logarytmicznej, której wykres jest symetryczny względem prostej $x = 7$ .

$y = \log_{3} "|"x + 7"|" + 1$
$y = \log_{3} "|"x - 7"|" + 1$
$y = \log_{3} ("|"x"|" - 7) + 1$
$y = \log_{3} ("|"x"|" + 7) + 1$

Ćwiczenie 6

Na podstawie wykresu funkcji $f (x) = \log_{3} x$ zaznacz, które zdanie jest prawdziwe a które fałszywe.

R9SREfQLGHCpu

Na podstawie wzoru funkcji $f (x) = \log_{3} x$ zaznacz, które zdanie jest prawdziwe a które fałszywe.

RMxbpxSEznuz8

	Prawda	Fałsz
Funkcja $y = \log_{3} ("\|"x"\|" - 2) - 1$ jest parzysta.	□	□
Wykres funkcji $y = \log_{3} ("\|"x"\|" - 2) - 1$ przecina oś $X$ w punktach $(- 5, 0)$ oraz $(5, 0)$ .	□	□
Asymptoty pionowe wykresu funkcji $y = \log_{3} ("\|"x"\|" - 2) - 1$ to proste o równaniach: $x = - 2, x = 2$ .	□	□

Ćwiczenie 7

Na podstawie wykresu funkcji $f (x) = \log_{\frac{1}{4}} x$ (rysunek poniżej) wybierz zdania prawdziwe.

Rn9AGZ7IBvEAi

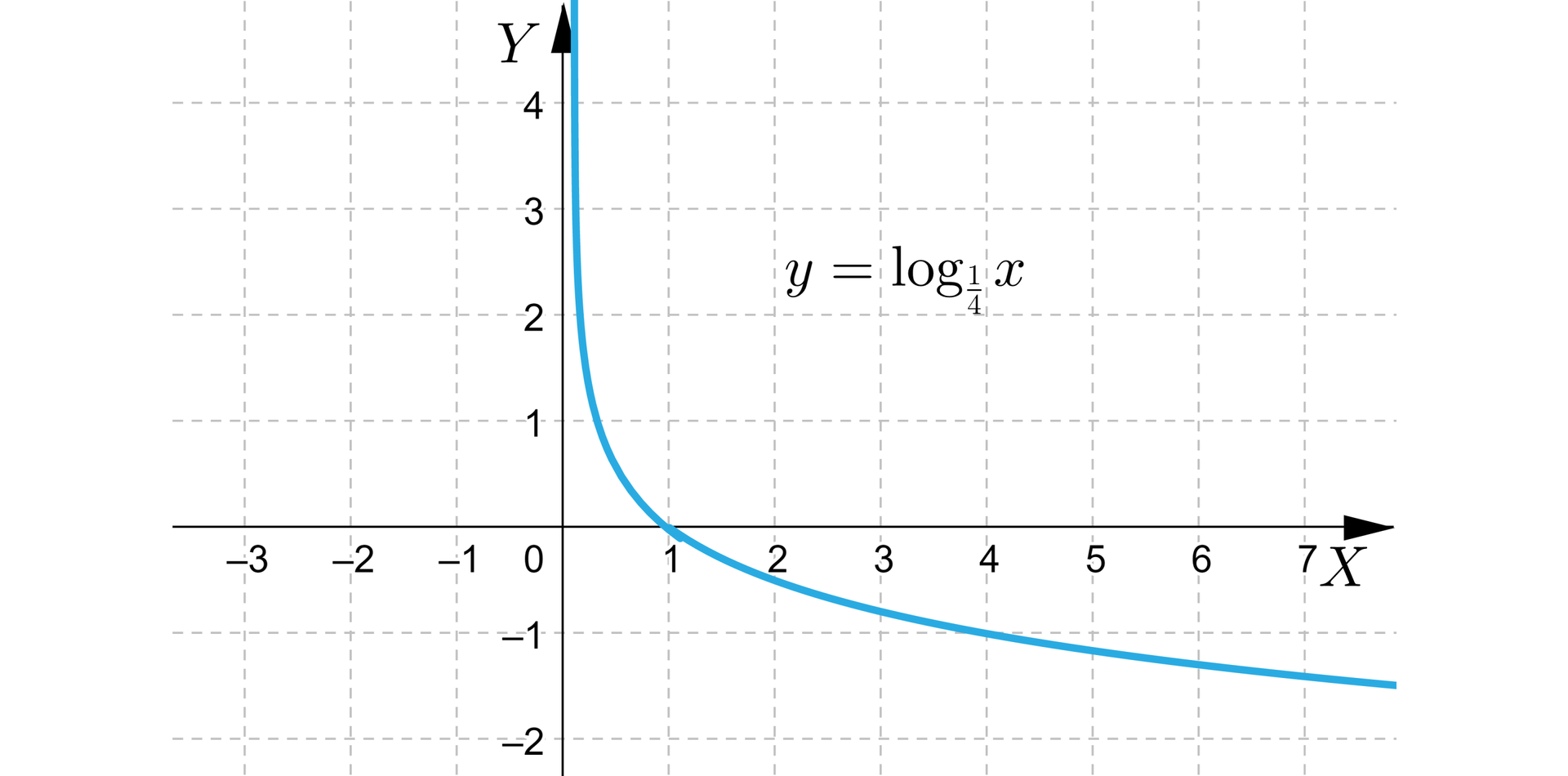
Ilustracja przedstawia układ współrzędnych z osią poziomą X od minus trzech do siedmiu i pionową Y od minus dwóch do czterech. Zaznaczono funkcję y=log14. Wykres funkcji znajduje się w pierwszej i czwartej ćwiartce układu współrzędnych. Wykres funkcji jest malejący i jest krzywą, która z lewej strony zbiega asymptotycznie do prostej x=0, a następnie przechodząc przez punkty: 1;0, 4;-1 dąży do nieskończoności.

RJbXtGcOBgAmV

Wykres funkcji $y = \log_{0, 25} (2 - "|"x"|")$ przecina oś $Y$ w punkcie $(0, \frac{1}{2})$ .
Wykres funkcji $y = \log_{0, 25} (2 - "|"x"|")$ przecina oś $X$ w punktach $(- 1, 0)$ oraz $(1, 0)$ .
Wykres funkcji $y = \log_{0, 25} (2 - "|"x"|")$ jest symetryczny względem prostej $x = 0$ .
Zbiorem wartości funkcji $y = \log_{0, 25} (2 - "|"x"|")$ jest przedział $⟨ - \frac{1}{2}, + \infty)$ .

Ćwiczenie 8

Dana jest funkcja $f (x) = \log_{4} x$ (rysunek poniżej). Wybierz zdanie prawdziwe.

R1BrTROR65FJ4

Dana jest funkcja $f (x) = \log_{4} x$ . Wybierz zdanie prawdziwe.

R14LvVbw4HsrW

Wykres funkcji $y = \log_{4} (4 - "|"x"|") + 3$ ma dwie asymptoty poziome: $y = - 4, y = 4$ .
Wykres funkcji $y = \log_{4} (4 - "|"x"|") + 3$ przecina oś $Y$ w punkcie $(0, 4)$ .
Zbiorem wartości funkcji $y = \log_{4} (4 - "|"x"|") + 3$ jest przedział $(- \infty, 4 ⟩$ .
Wykres funkcji $y = \log_{4} (4 - "|"x"|") + 3$ przecina oś $X$ w punkcie $(4, 0)$ .

Animacja

Dla nauczyciela