Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Ustaw zaznaczone na rysunku, kąty $α$ , $β$ , $γ$ w kolejności od najmniejszego do największego.

RGQW1qARPV2a8

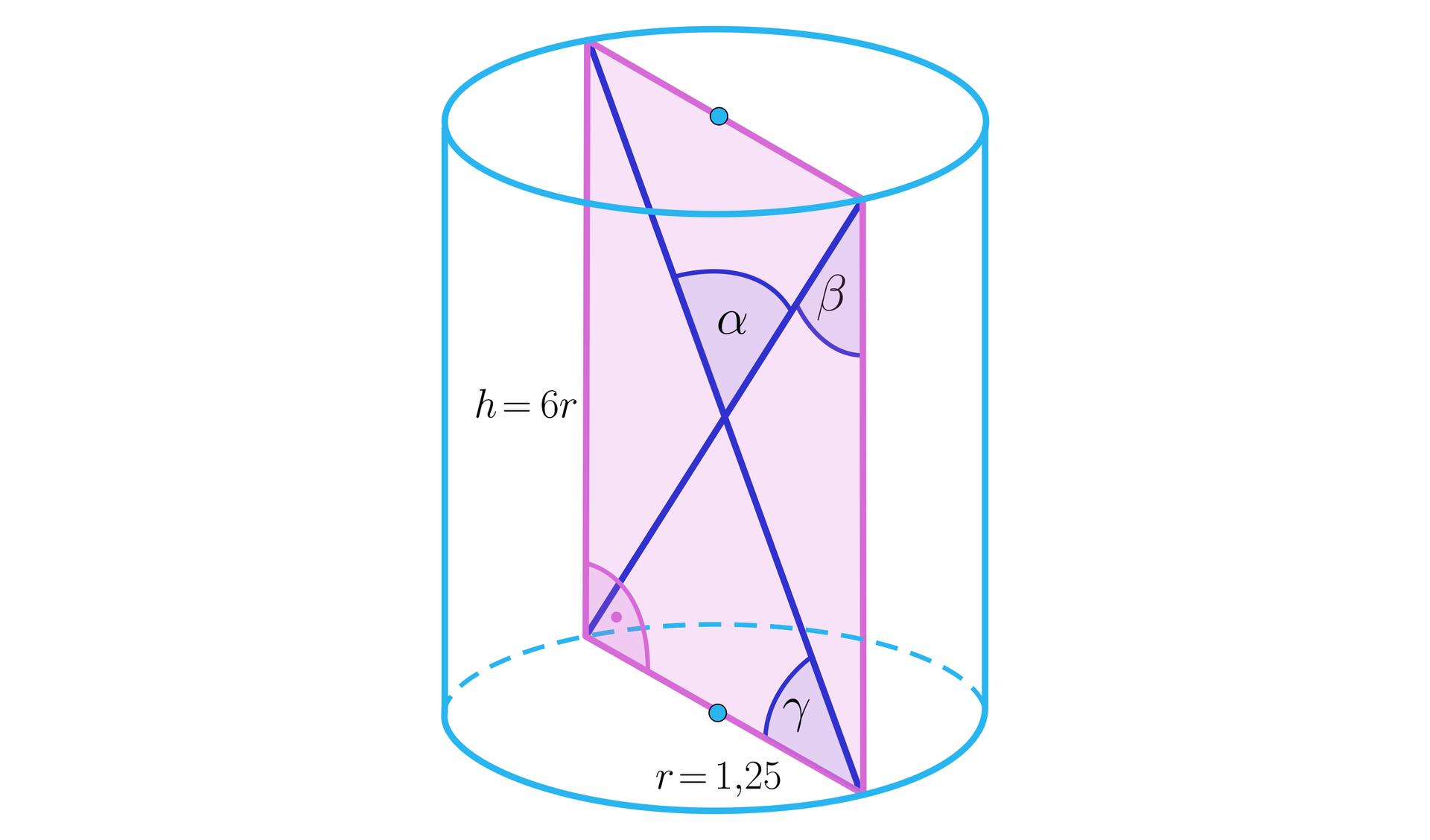
Ilustracja przedstawia walec oraz prostokąt znajdujący się wewnątrz bryły będącym jego przekrojem osiowym. W prostokącie o wymiarach h na dwa r, gdzie wysokość ma długość sześć r oraz promień podstawy r ma długość jeden przecinek dwadzieścia pięć, poprowadzono dwie przekątne. Zaznaczono także trzy kąty, pierwszy ostry kąt alfa znajduje się pomiędzy dwiema przekątnymi, drugi kąt beta znajduje się pomiędzy wysokością walca a przekątną prostokąta. Trzeci gamma znajduje się pomiędzy średnica walca a przekątną prostokąta.

R1El5shLfO6BG

$β$
$α$
$γ$

Ćwiczenie 2

Na rysunku przedstawiono kilka kątów pomiędzy odcinkami w walcu.

RfULoSeKnPdC3

Ry5ukn9sT9OXK

Łączenie par. . Suma kątów

β

δ

wynosi

180 °

.. Możliwe odpowiedzi: Prawda, Fałsz. Jeżeli promień podstawy jest krótszy od wysokości, to kąt

α

jest ostry.. Możliwe odpowiedzi: Prawda, Fałsz. Jeżeli punkt przecięcia przekątnych przekroju na rysunku połączymy z punktami na brzegu jednej z podstaw, to kąt .. Możliwe odpowiedzi: Prawda, Fałsz. Ostrosłup jest prawidłowy.. Możliwe odpowiedzi: Prawda, Fałsz

Oceń prawdziwość zdań.

	Prawda	Fałsz
Suma kątów $β$ i $δ$ wynosi $180 °$ .	□	□
Jeżeli średnica podstawy jest krótsza od wysokości, to kąt $α$ jest ostry.	□	□
Jeżeli punkt przecięcia przekątnych przekroju na rysunku połączymy z punktami na brzegu jednej z podstaw, to kąt $α$ między przekątnymi tego przekroju jest kątem rozwarcia stożka powstałego w ten sposób.	□	□
Kąty $β$ i $δ$ mają tę samą miarę.	□	□

RXQBuMFHl8krj1

Ćwiczenie 3

Wysokość walca jest czterokrotnie dłuższa od promienia podstawy. Wówczas kąt pomiędzy przekątną przekroju osiowego a tworzącą walca ma miarę:

około $27 °$
$30 °$
$60 °$
około $63 °$

R2jFFhPuGOyWQ2

Ćwiczenie 4

Zaznacz wszystkie poprawne odpowiedzi.
Kąt pomiędzy przekątnymi przekroju osiowego walca ma miarę $90 °$ . A zatem:

przekrój osiowy jest kwadratem.
przekrój osiowy jest rombem o kątach różnej miary.
promień podstawy jest dwukrotnie dłuższy od wysokości.
wysokość walca jest dwukrotnie dłuższa od promienia podstawy.

R1OOWYtozrD3O2

Ćwiczenie 5

Powierzchnia boczna walca po rozwinięciu jest prostokątem o wymiarach $4 π \times 8 π$ . Jaką miarę może mieć kąt pomiędzy przekątną przekroju tego walca a średnicą podstawy? Wybierz wszystkie poprawne odpowiedzi.

Około $58 °$
Około $72 °$
Około $18 °$
Około $81 °$

R19Tef1LnNDQ92

Ćwiczenie 6

Objętość walca wynosi $6 π$ . Kąt pomiędzy przekątną przekroju osiowego a średnicą jest dwukrotnie mniejszy od kąta pomiędzy przekątną przekroju osiowego a wysokością. Pole podstawy tego walca wynosi:

$3 π$
$4 π$
$8 π$
$6 π$

Ćwiczenie 7

Walec przecięto w odległości $7$ od środka płaszczyzną prostopadłą do podstaw otrzymując czworokąt $A B C D$ . Cosinus kąta $A S B$ (gdzie $S$ jest środkiem podstawy, na brzegu której leżą punkty $A$ i $B$ ) wynosi $(- 0, 8432)$ . Kąt nachylenia przekątnej tego przekroju do tworzącej ma miarę $30 °$ . Oblicz pole powierzchni tego walca.

Zróbmy rysunek pomocniczy i wprowadźmy na nim oznaczenia.

RPPZt73YDCCyL

Ilustracja przedstawia walec oraz prostokąt A B C D znajdujący się wewnątrz bryły będącym jego przekrojem. W prostokącie A B C D poprowadzono przekątną pod kątem trzydziestu stopni do wysokości walca B C. W podstawie walca powstał trójkąt równoramienny A B S z wysokością poprowadzoną z wierzchołka S, który równocześnie jest środkiem podtawy, upuszczoną na bok A B w punkcie L.

Kąt $L S B$ na rysunku ( $L$ jest środkiem odcinka $A B$ ) jest dwukrotnie mniejszy od kąta $A S B$ , a zatem $\cos (∢ A S B) = 2 \cos^{2} (∢ L S B) - 1$ . Stąd $\cos^{2} (∢ L S B) = \frac{- 0, 8432 + 1}{2} = 0, 0784$ . A zatem $\cos (∢ L S B) = 0, 28$ . Mamy więc $\frac{|L S|}{|S B|} = 0, 28$ . Czyli $\frac{7}{|S B|} = 0, 28$ i ostatecznie $|S B| = 25$ .

Z twierdzenia Pitagorasa obliczymy długość odcinka $L B : {|L B|}^{2} + 7^{2} = 25^{2}$ . A stąd $|L B| = 24$ . Czyli $|A B| = 48$ . Z trójkąta $B C D$ mamy $\frac{48}{|B C|} = tg 30 °$ . Stąd $|B C| = 48 \sqrt{3}$ .

Mamy więc $r = 25$ i $h = 48 \sqrt{3}$ .

A zatem $P_{c} = 2 \cdot 25^{2} π + 2 π \cdot 25 \cdot 48 \sqrt{3} = 1250 π + 2400 \sqrt{3} π = 50 π (25 + 48 \sqrt{3})$ .

Ćwiczenie 8

Czworokąty $A B C D$ i $A D E F$ są przystającymi przekrojami prostopadłymi do podstaw walca o promieniu $2$ i wysokości $4$ . Odcinek $E C$ jest średnicą podstawy. Oblicz miarę kąta pomiędzy odcinkami $F D$ i $B D$ .

Zróbmy rysunek pomocniczy.

R1WsIuAb9ejiH

Ilustracja przedstawia walec oraz dwa prostokąty A B C D oraz A D E F będącymi przekrojami prostopadłymi do podstawy walca. Odcinki F B i E C są średnicami walca, natomiast odcinki B C i F E są jego wysokościami. Z wierzchołków B oraz F znajdujących się w dolnej podstawie figury proste ograniczone punktem D znajdującym się w górnej podstawie walca. Powstał trójkąt równoramienny B F D gdzie ramionami są odcinki D B oraz F D ustawione do siebie pod kątem alfa.

Ponieważ odcinek $E C$ jest średnicą, to odcinek $F B$ również jest średnicą podstawy, a to oznacza, że $B A F$ jest trójkątem prostokątnym. Przekroje $A B C D$ i $A D E F$ są przystające, a zatem trójkąt $B A F$ jest również równoramienny. Mamy więc $|A B| = |A F| = 2 \sqrt{2}$ . Obliczmy długość odcinków $F D$ i $B D$ – są to przekątne zaznaczonych przekrojów. Skorzystajmy z twierdzenia Pitagorasa.

Mamy zatem: ${|B D|}^{2} = {|A B|}^{2} + {|A D|}^{2}$ , a stąd $| B D | = \sqrt{8 + 16} = \sqrt{24} = 2 \sqrt{6}$ .

Do obliczenia miary kąta $α$ skorzystamy z twierdzenia cosinusów w trójkącie $B D F$ . Czyli:

${|B F|}^{2} = {|B D|}^{2} + {|F D|}^{2} - 2 |B D| \cdot |F D| \cos α$

A stąd $16 = 24 + 24 - 48 \cos α$ . Co daje nam $\cos α = \frac{32}{48} = \frac{2}{3} \approx 0, 6667$ , czyli $α \approx 48 °$ .

Aplet

Dla nauczyciela