Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

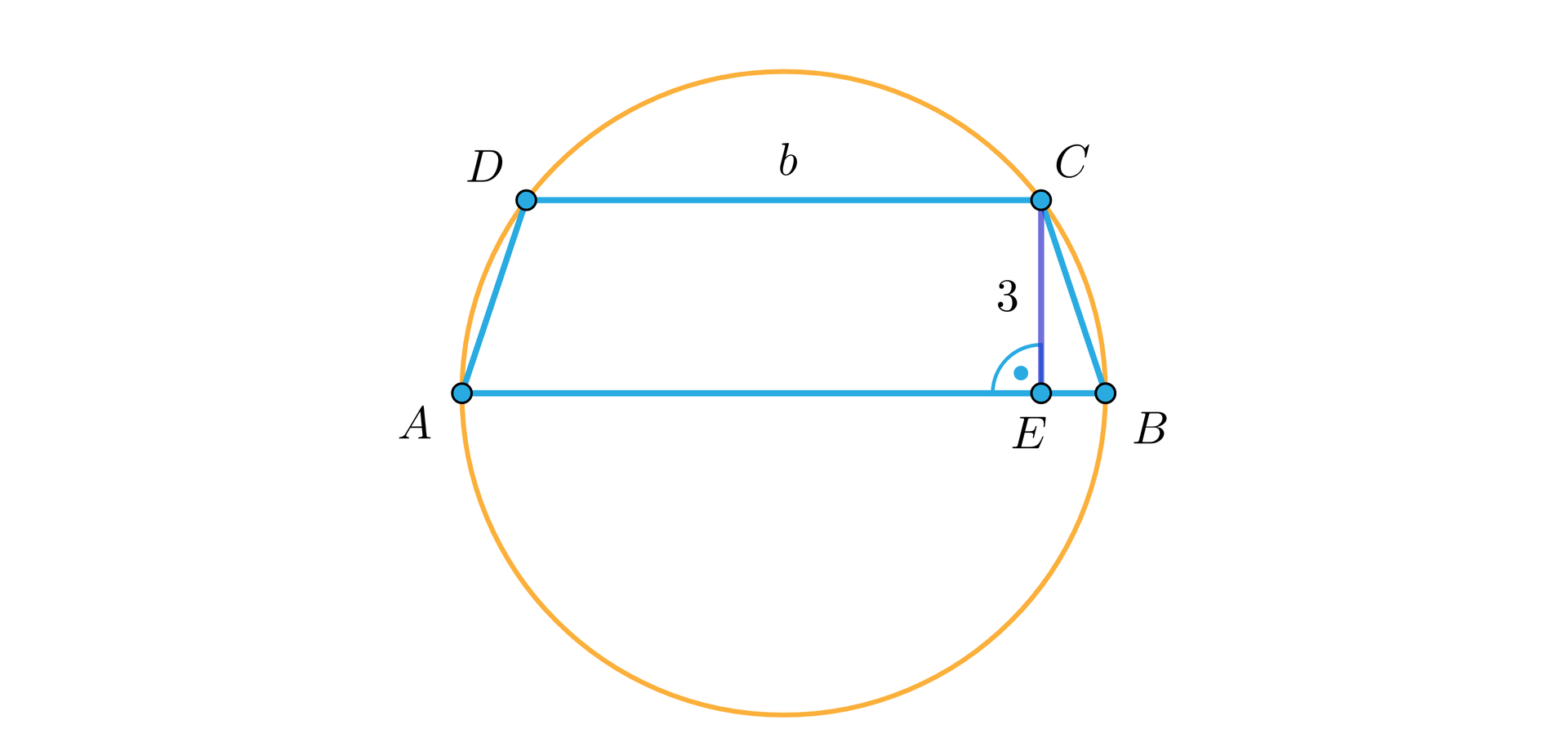
Podstawa $A B$ trapezu $A B C D$ jest średnicą okręgu o promieniu $5$ , na nim opisanego. Wysokość tego trapezu jest równa $3$ . Oblicz pole trapezu.

Trapez wpisany w okrąg jest trapezem równoramiennym. Przyjmijmy oznaczenia, jak na rysunku.

R1eyDRtyLTVGj

Ilustracja przedstawia trapez A B C D wpisany w okrąg. Krótsza podstawa DC ma długość b, a wysokość CE ma długość trzy.

Punkt $E$ jest spodkiem wysokości, zatem z własności trójkąta prostokątnego mamy:

$|A E| \cdot |B E| = {|C E|}^{2}$ , czyli $(10 - |B E|) \cdot |B E| = 3^{2}$ .

Pozwala to zapisać równanie kwadratowe ${|B E|}^{2} - 10 |B E| + 9 = 0$ .

Jego pierwiastkami są liczby: $1$ oraz $9$ .

Stąd $b = 10 - 2 = 8$ , a pole jest równe $P = \frac{10 + 8}{2} \cdot 3 = 27$ .

Ćwiczenie 2

W okrąg wpisano deltoid $A B C D$ o bokach długości $5$ i $4$ . Oblicz pole tego deltoidu.

Ponieważ jest to czworokąt cykliczny, więc można „od razu” skorzystać ze wzoru Brahmagupty.

Wtedy połowa obwodu deltoidu jest równa $9$ , a pole $P = \sqrt{(9 - 5) (9 - 4) (9 - 5) (9 - 4)} = 4 \cdot 5 = 20$ .

Oczywiście nie jest konieczne korzystanie ze wzoru Brahmagupty, wystarczy zauważyć, że z własności deltoidu i z twierdzenia o czworokącie wpisanym w okrąg wynika, że dwa przeciwległe jego kąty muszą być kątami prostymi. Wtedy oś symetrii deltoidu jest przeciwprostokątną dwóch przystających trójkątów o przyprostokątnych $5$ i $4$ . Pole każdego z tych trójkątów jest równe
$P_{△} = \frac{5 \cdot 4}{2} = 10$ , zatem pole deltoidu jest równe $20$ .

R15mlk21HJPNb1

Ćwiczenie 3

Zaznacz poprawną odpowiedź. Pole czworokąta wpisanego w okrąg, którego boki mają długości $"|"A B"|" = 4$ , $"|"B C"|" = 4$ , $"|"C D"|" = 8$ , $"|"A D"|" = 6$ jest równe:

$72 \sqrt{14}$
$7 \sqrt{15}$
$16 \sqrt{3}$
$\sqrt{22}$

Ćwiczenie 4

W okrąg o promieniu $5$ wpisano deltoid o polu równym $40$ . Oblicz obwód tego deltoidu.

Przyjmijmy oznaczenia, jak na rysunku.

RxbSUqG3Qnbux

Ilustracja przedstawia deltoid A B C D wpisany w okrąg. Przekątne deltoidu przecinają się w punkcie E.

Wtedy $|A C| = 10$ . Korzystając ze wzoru na pole deltoidu otrzymujemy: $\frac{|A C| \cdot |B D|}{2} = 40$ , zatem $|B D| = 8$ .

Punkt $E$ jest punktem przecięcia się przekątnych deltoidu i środkiem odcinka $B D$ .

Jest też spodkiem wysokości poprowadzonej z wierzchołka $D$ w trójkącie prostokątnym $A D C$ .

Z własności trójkąta prostokątnego wynika, że $|A E| \cdot |C E| = {|D E|}^{2}$ , czyli $|C E| \cdot (10 - |C E|) = {(\frac{1}{2} |B D|)}^{2}$ .

Pozwala to zapisać równanie kwadratowe ${|C E|}^{2} - 10 |C E| + 16 = 0$ .

Jego pierwiastkami są liczby: $2$ oraz $8$ .

Zatem ${|D C|}^{2} = 4^{2} + 2^{2} = 20$ oraz ${|A D|}^{2} = 4^{2} + 8^{2} = 80$ .

Obwód jest więc równy: $2 \sqrt{20} + 2 \sqrt{80} = 12 \sqrt{5}$ .

Ćwiczenie 5

Na danym trapezie $A B C D$ , w którym $A B ∥ C D$ , można opisać okrąg. Kąty $α$ , $β$ , $γ$ , $δ$ są w podanej kolejności kątami wewnętrznymi tego trapezu, jak na rysunku.

R2L3v2WUuyETL

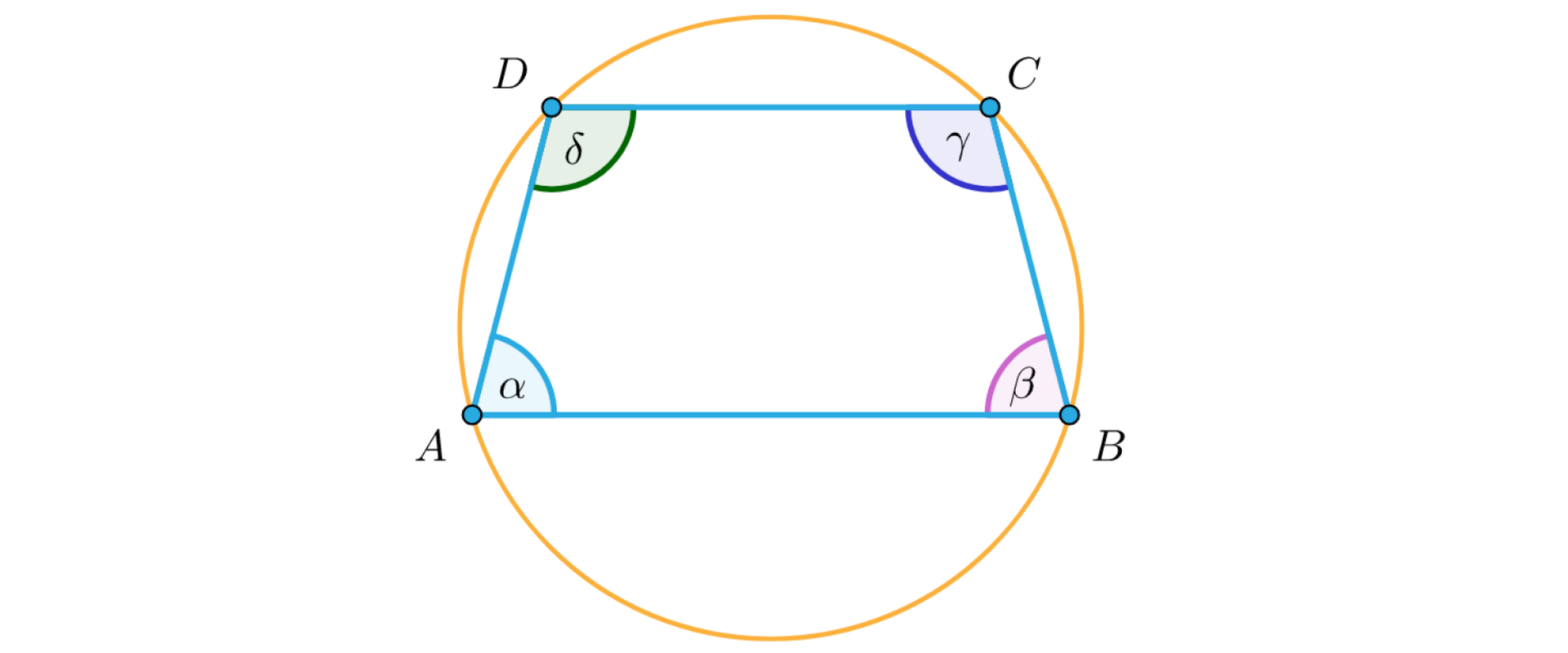
Ilustracja przedstawia trapez A B C D wpisany w okrąg. Kąt przy wierzchołku A wynosi alfa, przy wierzchołku B wynosi beta, przy wierzchołku C gamma, a przy wierzchołku D delta. Odcinki AB i DC to podstawy trapezu.

Korzystając z zapisanych zależności, wyznacz miary kątów danego trapezu.

R1W8kXQigFWga

Dopasuj zależności do miar kątów trapezu.

γ = 3 α

Możliwe odpowiedzi: 1.

α = 75 °, β = 75 °, γ = 105 °, δ = 105 °

, 2.

α = 60 °, β = 60 °, γ = 120 °, δ = 120 °

, 3.

α = 45 °, β = 45 °, γ = 135 °, δ = 135 °

γ - α = 30 °

Możliwe odpowiedzi: 1.

α = 75 °, β = 75 °, γ = 105 °, δ = 105 °

, 2.

α = 60 °, β = 60 °, γ = 120 °, δ = 120 °

, 3.

α = 45 °, β = 45 °, γ = 135 °, δ = 135 °

α + 2 β = \frac{3}{2} δ

Możliwe odpowiedzi: 1.

α = 75 °, β = 75 °, γ = 105 °, δ = 105 °

, 2.

α = 60 °, β = 60 °, γ = 120 °, δ = 120 °

, 3.

α = 45 °, β = 45 °, γ = 135 °, δ = 135 °

Dopasuj zależności do miar kątów trapezu.

$γ = 3 α$
$γ - α = 30 °$
$α + 2 β = \frac{3}{2} δ$

RGyE9iP6YJTp82

Ćwiczenie 6

W czworokąt cykliczny $A B C D$ , o bokach długości $a$ , $b$ , $c$ , $d$ , można wpisać okrąg. Udowodnij, że pole tego czworokąta można wyrazić wzorem $P = \sqrt{a b c d}$ .
Ułóż w kolejności etapy dowodu.
Dowód:

$p - b = \frac{a + b + c + d}{2} - b = \frac{a + c + d - b}{2} = \frac{(a + c) + d - b}{2} = \frac{b + d + d - b}{2} = d$
Zatem iloczyn $(p - a) (p - b) (p - c) (p - d)$ jest równy $a \cdot b \cdot c \cdot d$ . Co kończy dowód.
Pole czworokąta cyklicznego opisuje wzór Brahmagupty: $P = \sqrt{(p - a) (p - b) (p - c) (p - d)}$ .
Ponieważ $2 p = a + b + c + d$ , więc każdy z czynników $(p - a)$ , $(p - b)$ , $(p - c)$ , $(p - d)$ możemy przekształcić, otrzymując kolejno:
Przyjmijmy, że $a$ , $b$ , $c$ , $d$ są długościami kolejnych boków czworokąta.
W czworokąt o danych bokach można wpisać okręg tylko wtedy, gdy $a + c = b + d$ .
$p - c = \frac{a + b + c + d}{2} - c = \frac{a + b + d - c}{2} = \frac{(b + d) + a - c}{2} = \frac{a + c + a - c}{2} = a$
$p - a = \frac{a + b + c + d}{2} - a = \frac{b + c + d - a}{2} = \frac{(b + d) + c - a}{2} = \frac{a + c + c - a}{2} = c$
$p - d = \frac{a + b + c + d}{2} - d = \frac{a + b + c - d}{2} = \frac{(a + c) + b - d}{2} = \frac{b + d + b - d}{2} = b$

Ćwiczenie 7

Kolejne boki czworokąta wpisanego w okrąg mają długości: $|A B| = 4$ , $|B C| = 4$ , $|C D| = 3 + \sqrt{21}$ , $|A D| = 6$ . Wyznacz miarę kąta $A B C$ .

Oznaczmy przez $p$ przekątną $A C$ , a przez $α$ miarę kąta $A B C$ .

Wtedy, korzystając dwukrotnie z twierdzenia cosinusów mamy:

$p^{2} = 4^{2} + 4^{2} - 2 \cdot 4 \cdot 4 \cdot \cos α$ ,

$p^{2} = 6^{2} + {(3 + \sqrt{21})}^{2} - 2 \cdot 6 \cdot (3 + \sqrt{21}) \cdot \cos (180 ° - α)$ .

Stąd $4^{2} + 4^{2} - 2 \cdot 4 \cdot 4 \cdot \cos α = 6^{2} + {(3 + \sqrt{21})}^{2} - 2 \cdot 6 \cdot (3 + \sqrt{21}) \cdot \cos (180 ° - α)$

czyli

$\cos α (12 \sqrt{21} + 68) = - 6 \sqrt{21} - 34$ .

Zatem $\cos α = - \frac{1}{2}$ i $α = 120 °$ .

RbQI0ZFCoxQeU3

Ćwiczenie 8

Łączenie par. Oceń prawdziwość poniższych zdań.. Każdy trapez równoramienny jest czworokątem cyklicznym.. Możliwe odpowiedzi: Prawda, Fałsz. Każdy romb jest czworokątem cyklicznym.. Możliwe odpowiedzi: Prawda, Fałsz. Istnieje czworokąt cykliczny, w którym miary kolejnych kątów różnią się o

40 °

.. Możliwe odpowiedzi: Prawda, Fałsz. Każdy czworokąt, którego dwa kąty są kątami prostymi jest wielokątem cyklicznym.. Możliwe odpowiedzi: Prawda, Fałsz. Każdy deltoid, w którym dwa kąty są kątami prostymi jest wielokątem cyklicznym.. Możliwe odpowiedzi: Prawda, Fałsz

Oceń prawdziwość poniższych zdań.

Zdanie	Prawda	Fałsz
Każdy trapez równoramienny jest czworokątem cyklicznym.	□	□
Każdy romb jest czworokątem cyklicznym.	□	□
Istnieje czworokąt cykliczny, w którym miary każdych dwóch sąsiednich kątów różnią się o $40 °$ .	□	□
Każdy czworokąt, którego dwa kąty są kątami prostymi jest wielokątem cyklicznym.	□	□
Każdy deltoid, w którym dwa kąty są kątami prostymi jest wielokątem cyklicznym.	□	□

Aplet

Dla nauczyciela