Sprawdź się
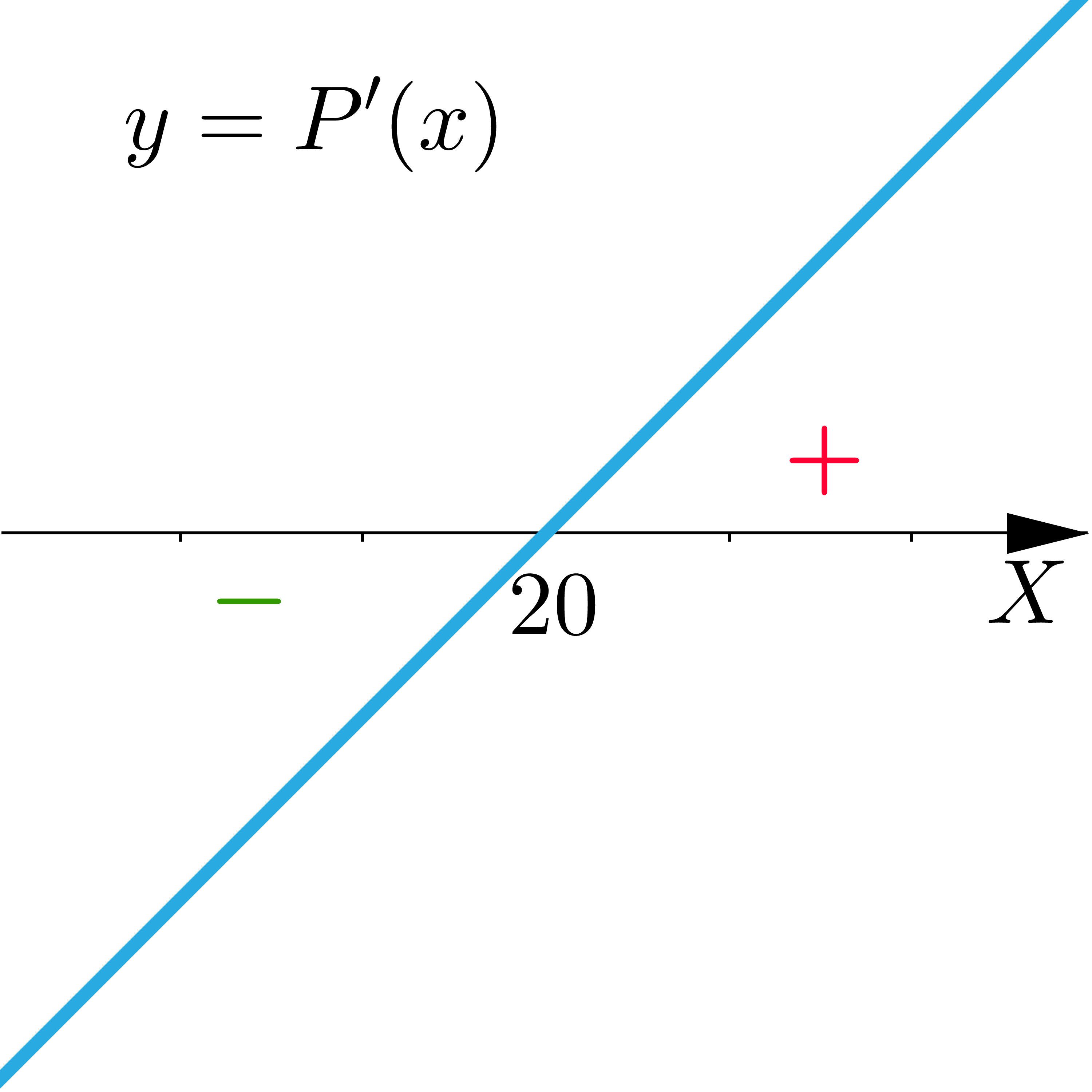
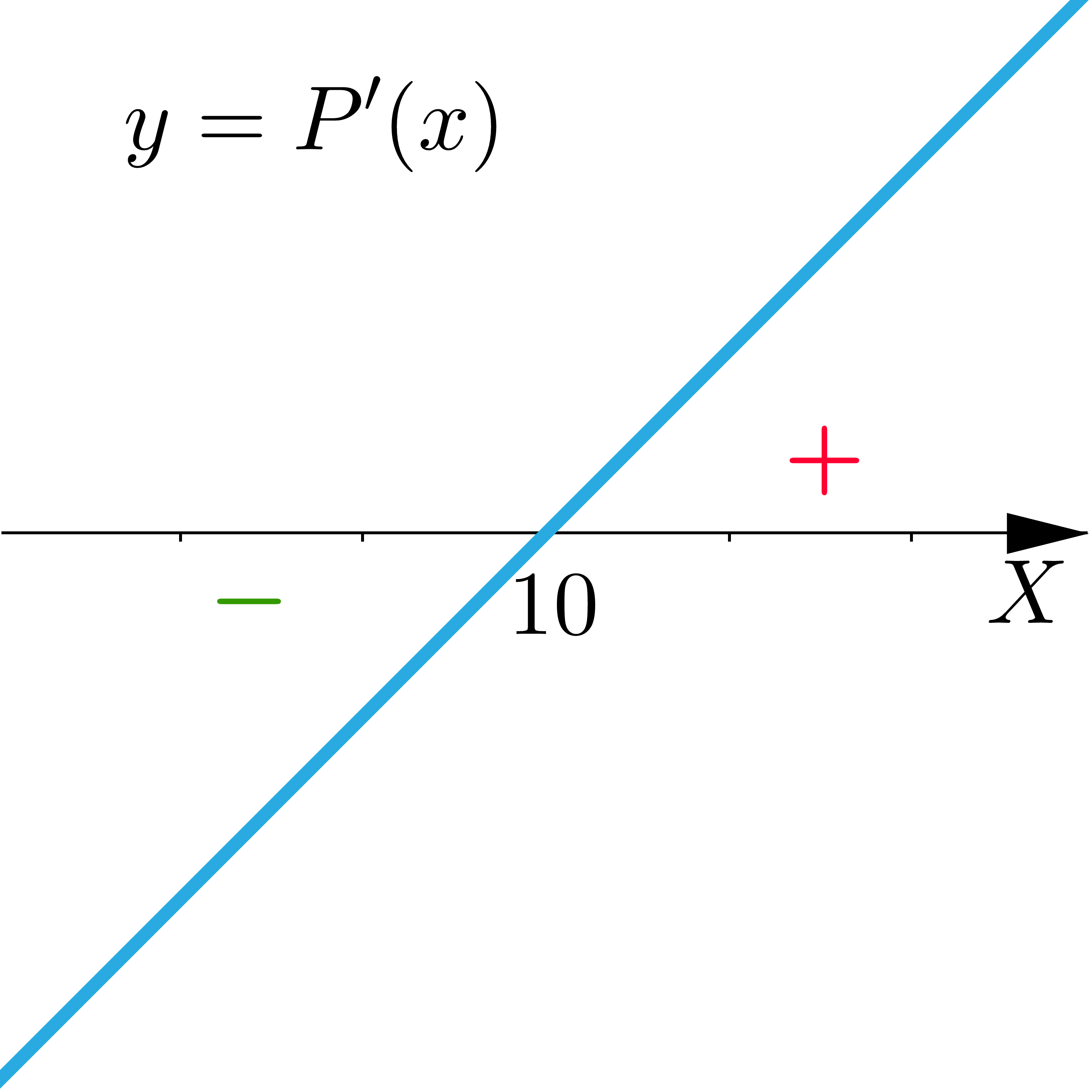
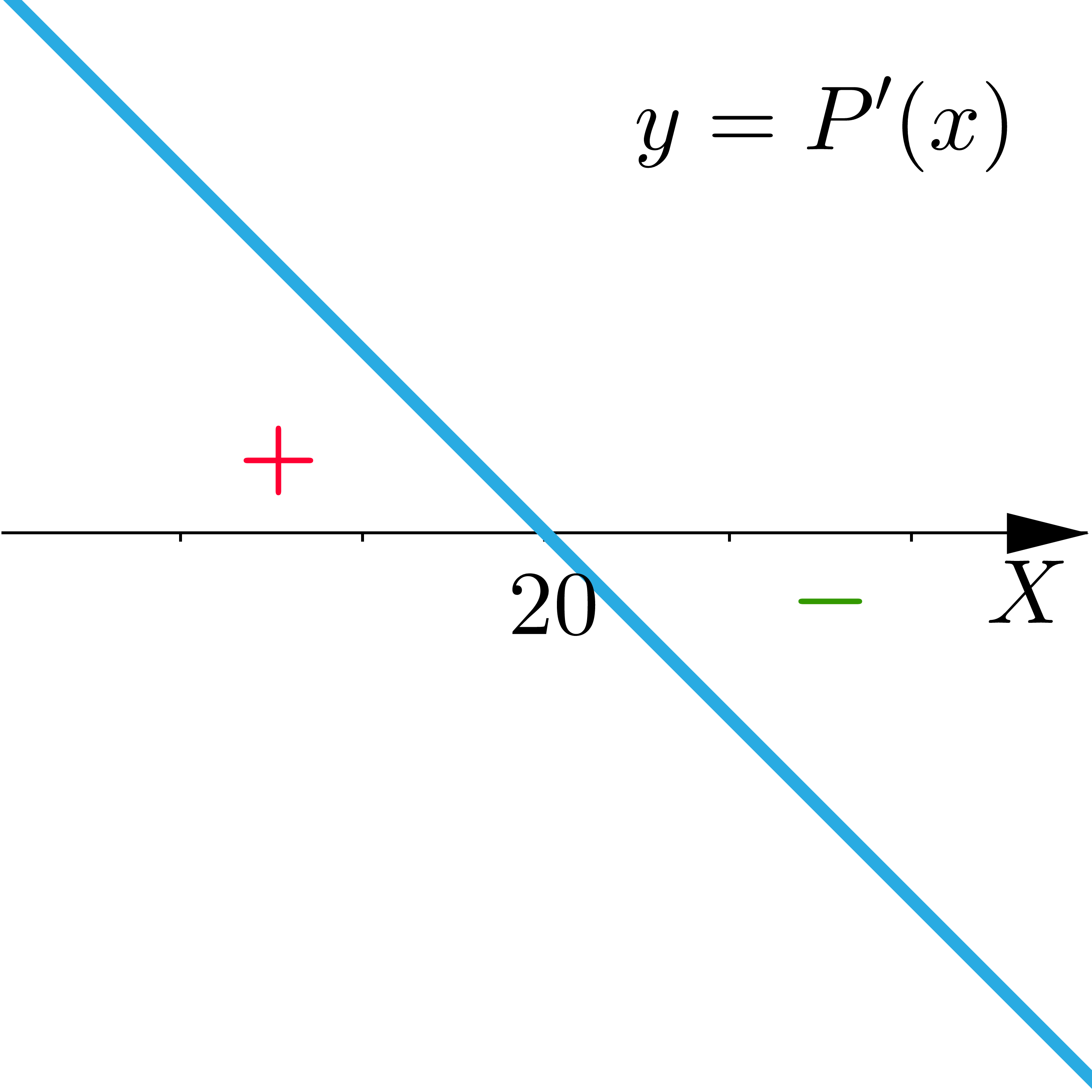
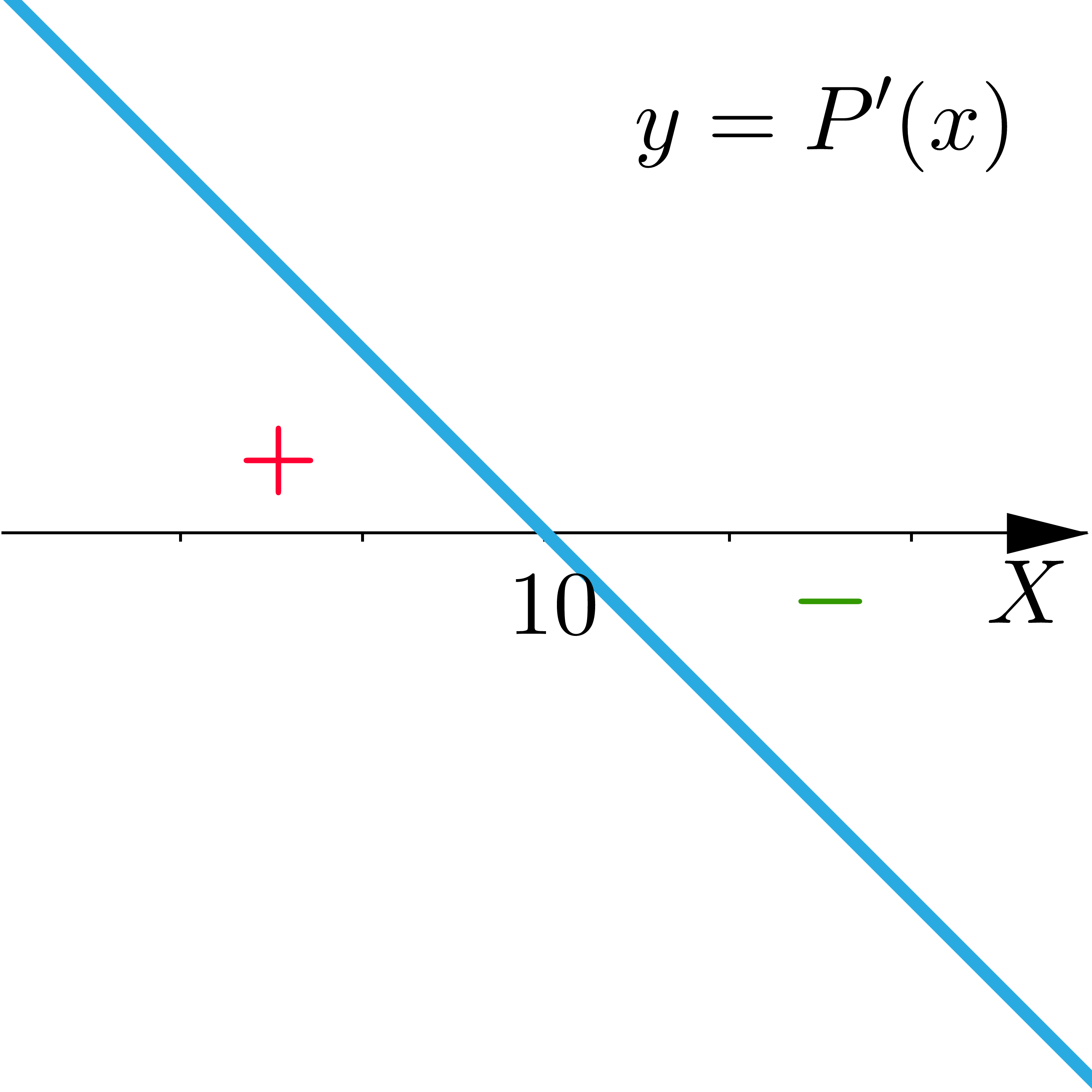
Suma długości dwóch boków równoległoboku wynosi , a kąt między bokami ma miarę . Wskaż wykres opisujący pochodną funkcji pola:
- Opis ilustracji A
- Opis ilustracji B
- Opis ilustracji C
- Opis poprawnej ilustracji D
Suma długości wysokości trapezu równoramiennego i obu jego podstaw jest równa . Największe możliwe pole wynosi:
Trapez równoramienny opisano na okręgu o promieniu . Uzupełnij tabelę wiedząc, że pole trapezu jest najmniejsze z możliwych. Przyjmij, że - długość krótszej podstawy.
MAX, BRAK, , , , , , , , , ,
Dane są punkty i . Na paraboli o równaniu znajdź taki punkt , aby pole trójkąta było najmniejsze.
W trójkącie równoramiennym suma długości ramienia i wysokości wynosi . Uzupełnij tabelę, wiedząc, że pole jest największe z możliwych. Przyjmij oznaczenie długość podstawy.
MIN, BRAK, , , , , , , , , , , , ,
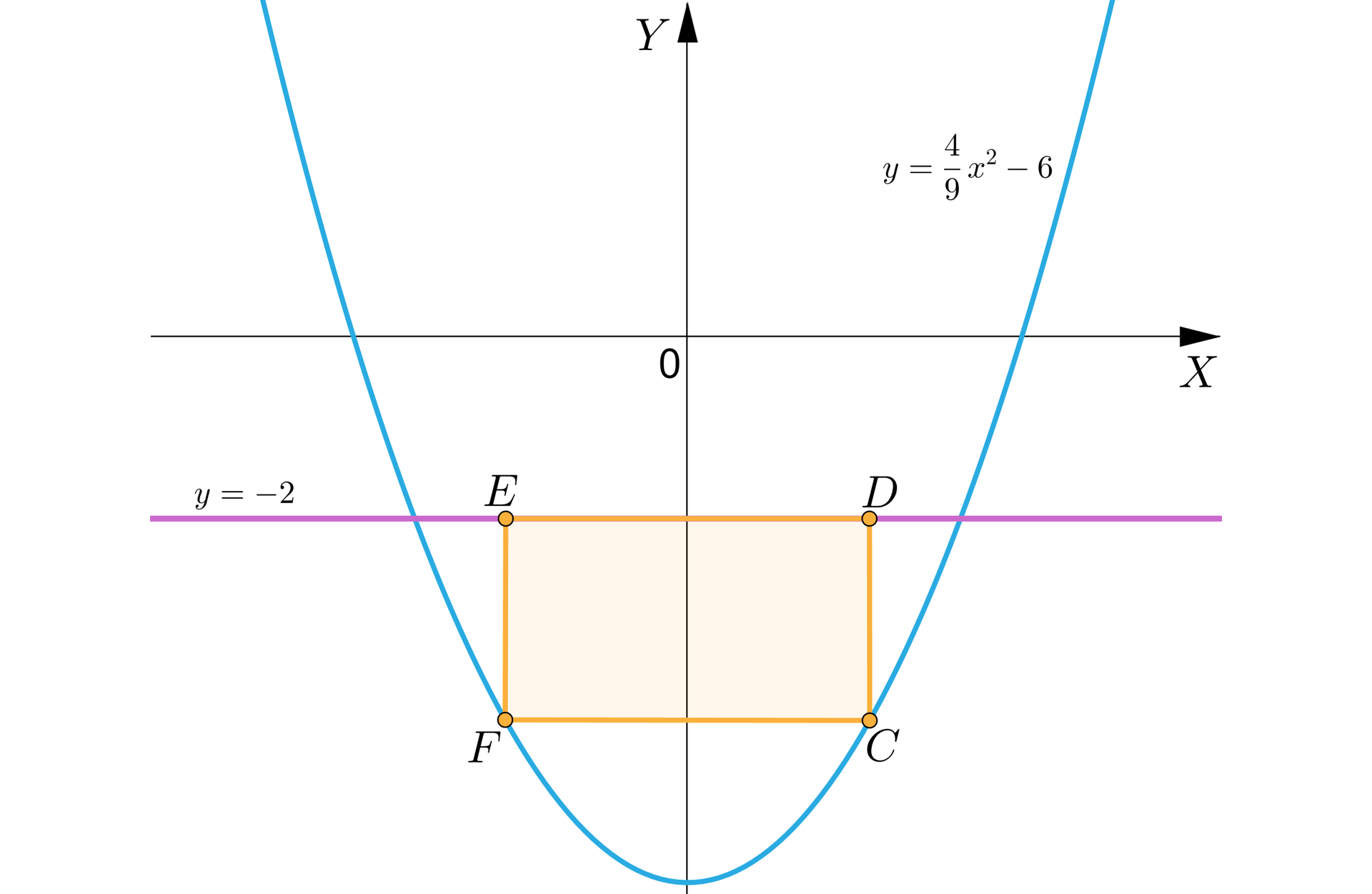
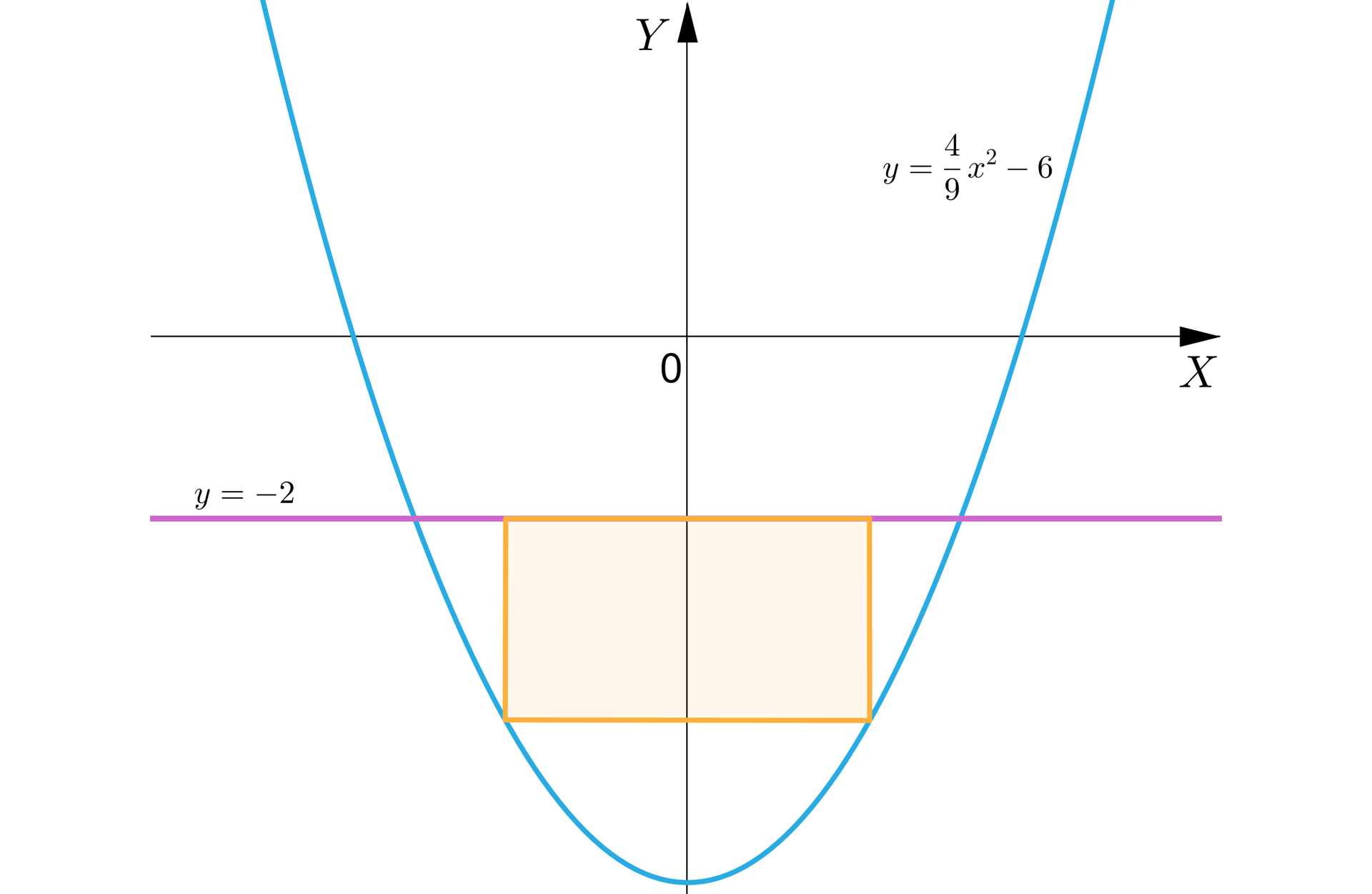
Dwa wierzchołki prostokąta należą do paraboli o równaniu , a dwa do prostej o równaniu (zobacz rysunek). Wyznacz długości boków prostokąta, którego pole powierzchni jest największe.
Dane są punkty , , , , gdzie .
a) Uzupełnij prawidłową odpowiedź. Pole czworokąta wynosi:
, , ,
........................
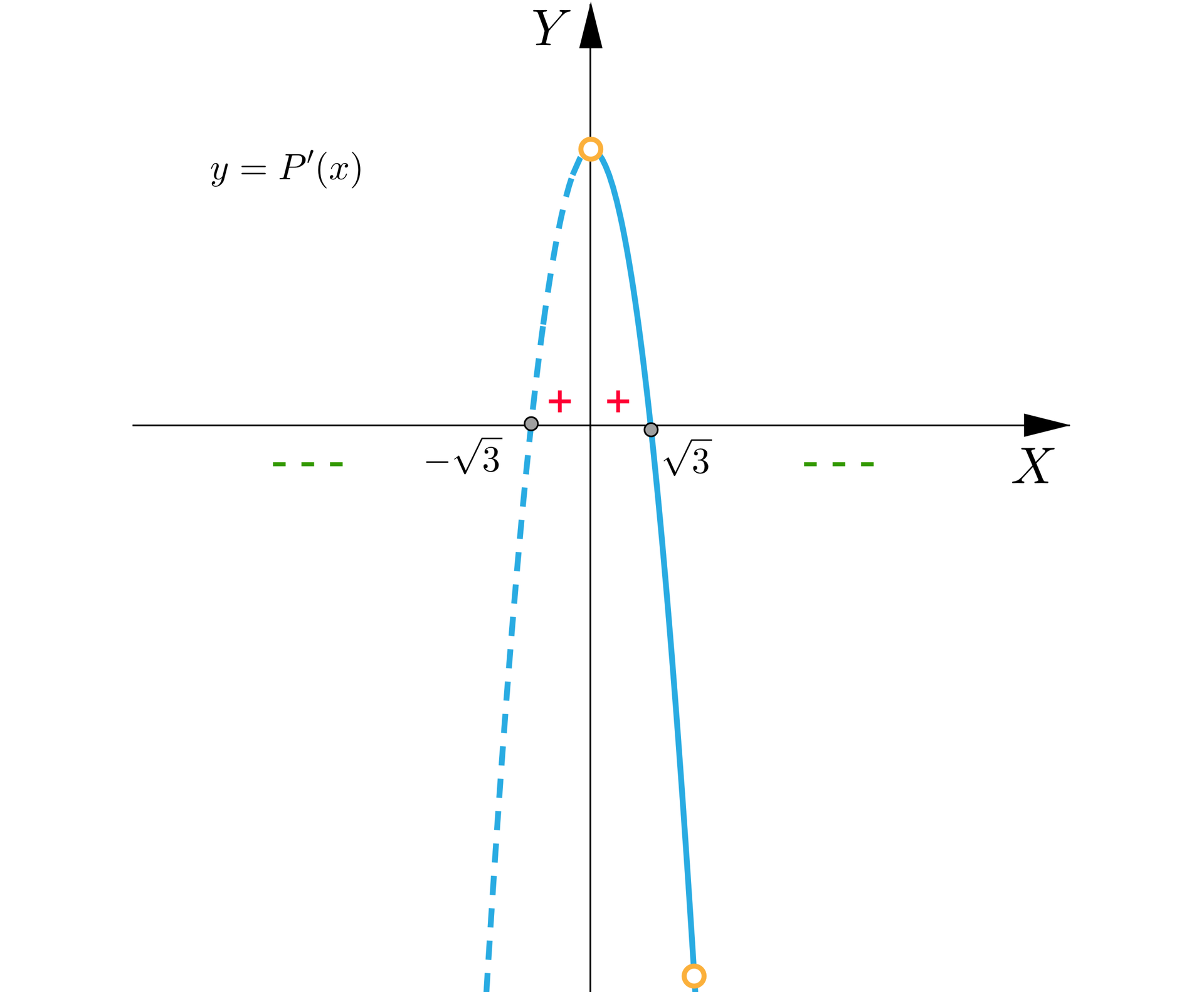
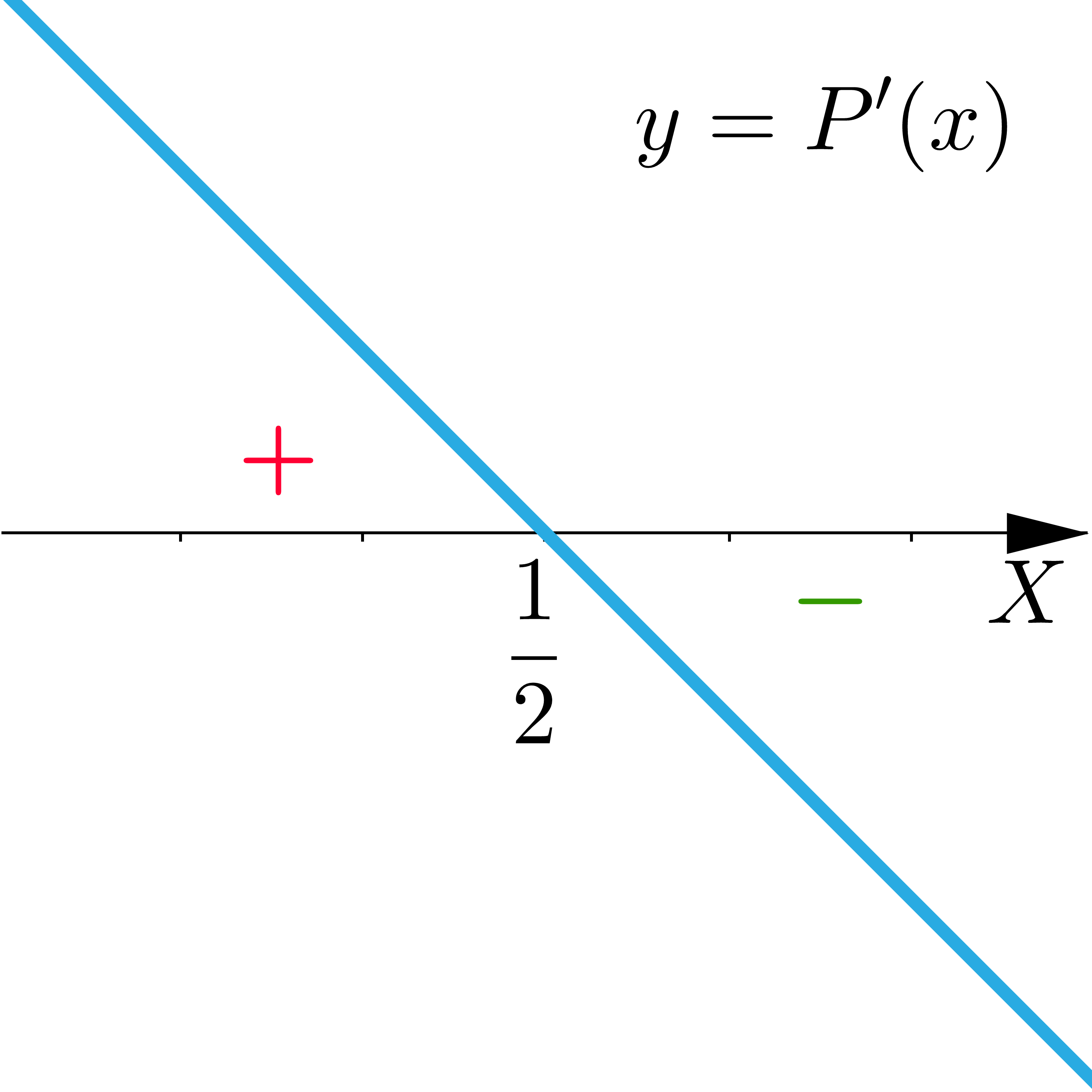
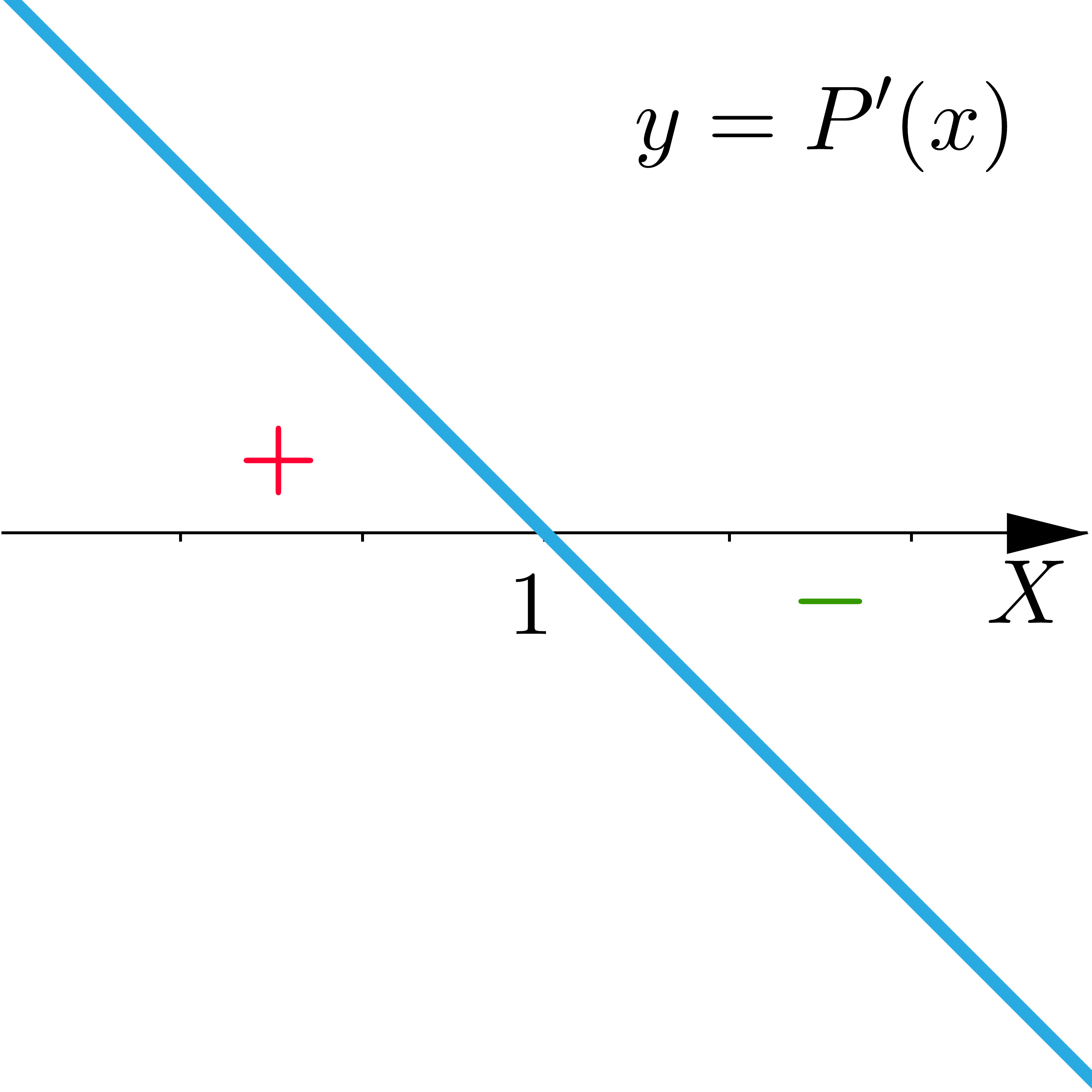
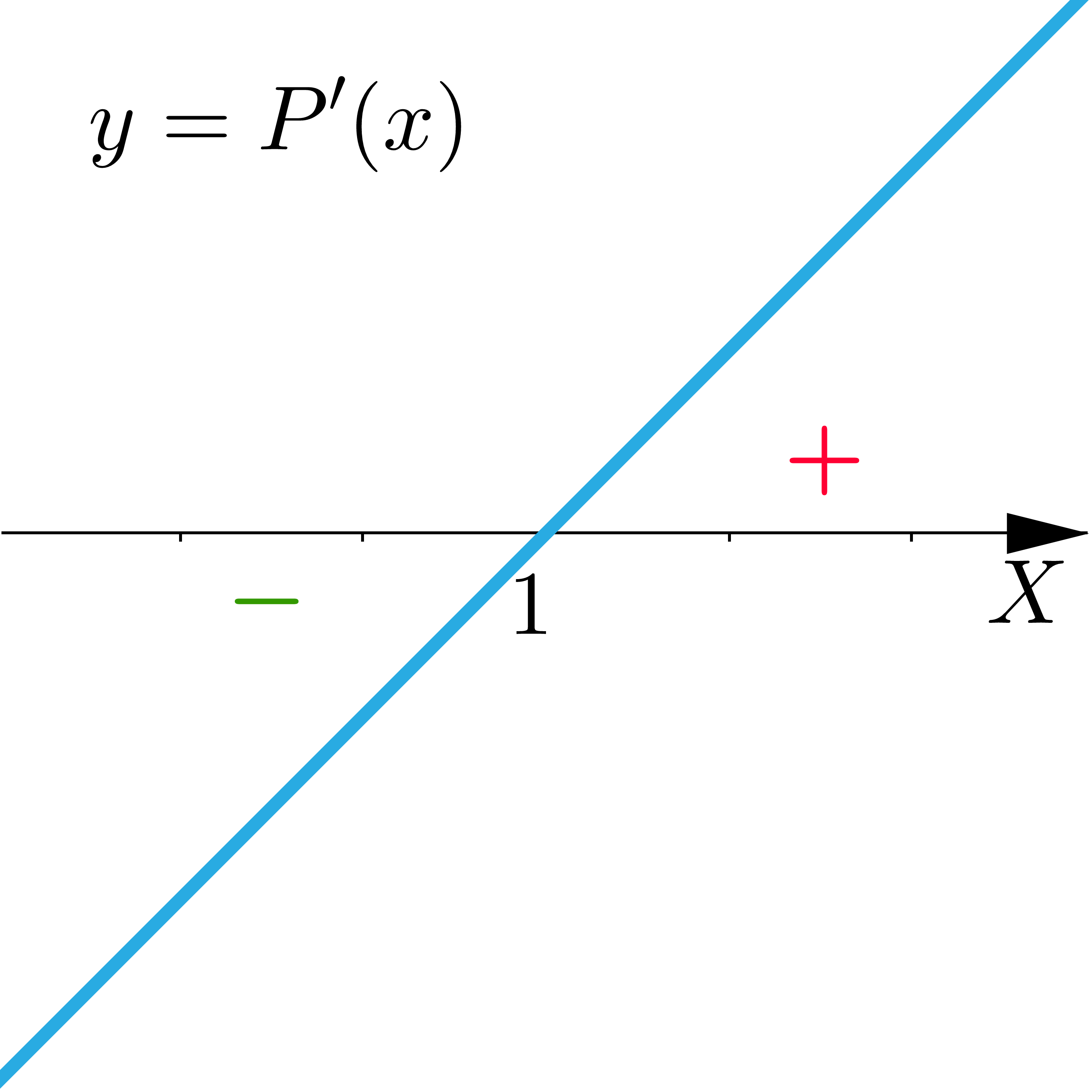
b) Wskaż wykres opisujący pochodną funkcji pola.
- Opis ilustracji A
- Opis poprawnej ilustracji B
- Opis ilustracji C
- Opis ilustracji D

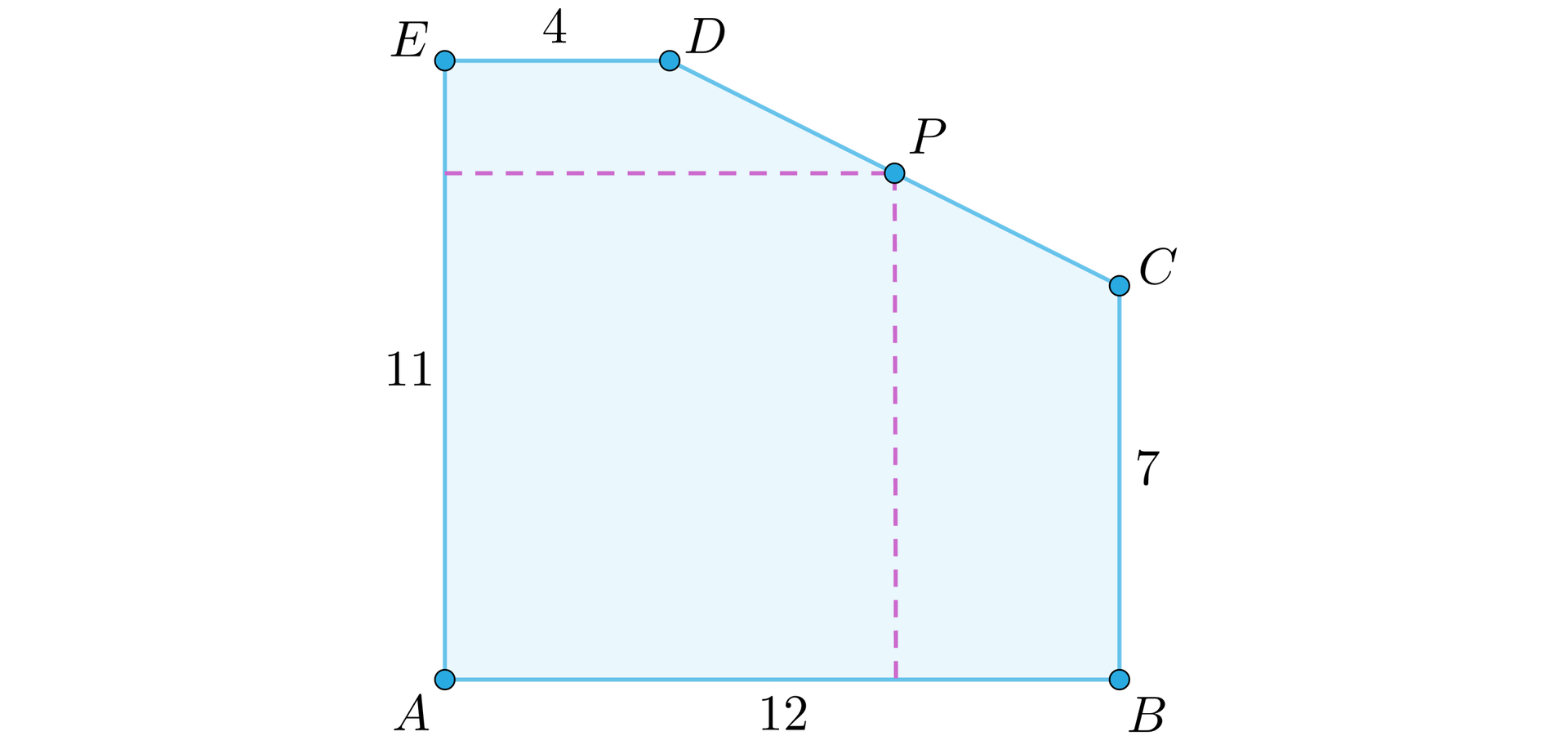
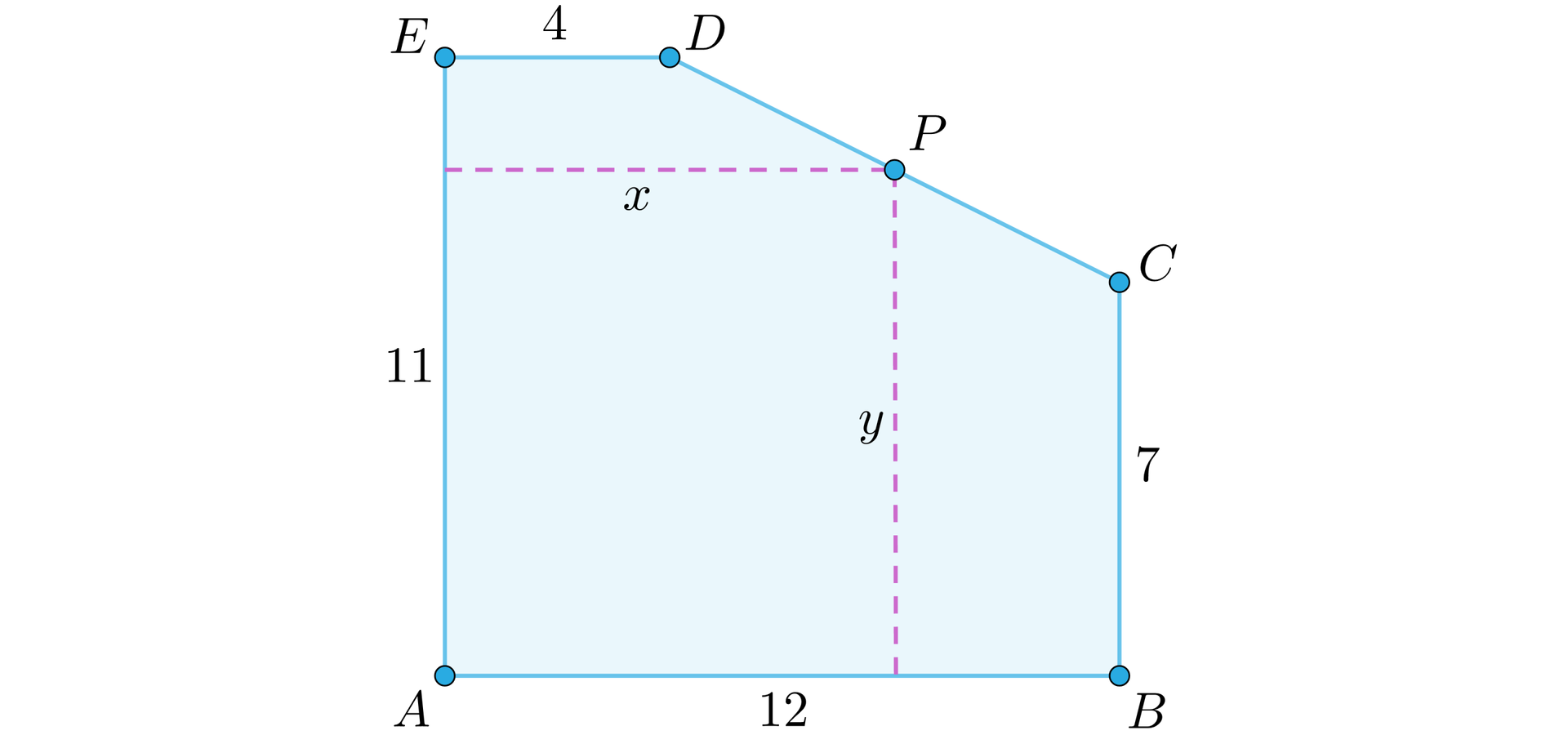
Z kawałka kartonu należy wyciąć prostokąt o jak największym polu, w taki sposób, by wierzchołek prostokąta należał do krawędzi (zobacz rysunek). Wyznacz wymiary tego prostokąta.